当前位置：文档之家 › 第二节 三相异步电动机的电磁转矩和机械特性

第二节 三相异步电动机的电磁转矩和机械特性

  • 格式：doc
  • 大小：1.17 MB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

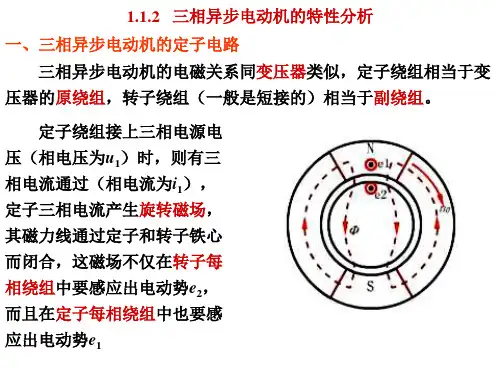
1.1.2三相异步电动机的转矩特性和机械特性

1.1.2三相异步电动机的转矩特性和机械特性
n电压的减小而大大地减小
Tst
随着电压的减小而大大地减小
改变电源电压时的人为特性如图所示： 改变电源电压时的人为特性如图所示：
三、转矩特性 电磁转矩（以下简称转矩） 电磁转矩（以下简称转矩）是三相异步电动机最重要的物理量 之一。机械特性是它的主要特性。 之一。机械特性是它的主要特性。
km1 pU 12 R2 s T= = Km1Φ I 2 cos ϕ 2 2 2 2 2πf1[ R2 + ( sX 20 ) ]
因为
I2 = S 4.44 f1 N 2Φ R2 + ( SX 20 )2
p( n0 − n ) n0 − n pn0 f2 = = = Sf1 60 n0 60
在 n=0 ，即S=1时，转子电动势为 时 E 20 = 4.44 f1 N 2Φ E 2 = SE 20 为转子最大电动势
可见转子电动势 与转差率S有关 有关。 可见转子电动势E2与转差率 有关。 电动势
和定子电流一样，转子电流也要产生漏磁通 漏磁通， 和定子电流一样，转子电流也要产生漏磁通，从而在转子每相 绕组中还要产生漏磁电动势。 绕组中还要产生漏磁电动势。 di 2 eL2 = − LL2 dt 因此，对于转子每相电路， 因此，对于转子每相电路，有 转子每相电路
（1）降低电动机电源电压 时的人为特性 ）降低电动机电源电压U1时的人为特性
60 f n0 = p n0 − nm R2 = Sm = X 20 n0 U2 Tmax = K 2 X 20 R2U 2 Tst = K 2 2 R2 + X 20 λ = Tmax TN
设定子和转子每相绕组的匝数分别为N1和 ， 设定子和转子每相绕组的匝数分别为 和 N2，如图所示电路 图是三相异步电动机的一相电路图 三相异步电动机的一相电路图。 图是三相异步电动机的一相电路图。

三相绕线式异步电动机各种运行状态下的机械特性

三相绕线式异步电动机各种运行状态下的机械特性

三相绕线式异步电动机各种运行状态下的机械特性原理简述机械特性是指其转速与转矩间的关系，一般表示为。

由于三相异步电动机的机械特性呈非线性关系，所以函数表达式以转速为自变量，转矩为因变量，写为更为方便。

又因转差率s也可以用来表征转速，而且用s表示的机械特性表达式更为简洁，所以对三相异步电动机一般用来表示机械特性，同时将作为横坐标，这样和原的图形是一致的。

一、三相异步电动机机械特性的表达式三相异步电动机机械特性的表达式一般有三种：1．物理表达式其中为异步电机的转矩常数；为每极磁通；为转子电流的折算值；为转子回路的功率因数。

2．参数表达式其中。

3．实用表达式其中为最大转矩，为发生最大转矩时的转差率。

三种表达式其应用场合各有不同，一般物理表达式适用于定性分析与及间的关系，参数表达式可以分析各参数变化对电动机运行性能的影响，而实用表达式最适合用于进行机械特性的工程计算。

二、三相异步电动机的机械特性1．固有机械特性固有机械特性是指异步电动机在额定电压、额定频率下，电动机按规定方法接线，定子及转子回路中不外接电阻（电抗或电容）时所获得的机械特性，如图15-1所示。

图15-1 三相异步电动机的固有机械特性下面对机械特性上反映其特点的几个特殊点进行分析：（1）起动点：其特点是：，，起动电流；（2）额定运行点：其特点是：，，；（3）同步速点：其特点是：，，，，点是电动状态与回馈制动的转折点；（4）最大转矩点：电动状态最大转矩点，其特点是：，；回馈制动最大转矩点，其特点是：，；由公式可以看出，。

2．人为机械特性由三相异步电动机机械特性的参数表达式可见，异步电动机的电磁转矩在某一转速下的数值，是由电源电压、频率、极对数及定转子电路的电阻、电抗、、、决定的。

因此人为的改变这些参数，就可得到不同的人为机械特性。

现介绍改变某些参数时人为机械特性的变化：（1）降低电压不变，不变，因为，，，所以降低电压时，、、均减小，其人为机械特性见图15-2。

吉林大学电工学1第7章 电动机

吉林大学电工学1第7章 电动机
返回
起动瞬间 n=0，s=1
R2↑→I2↓→Ist↓ R2↑→ Tst ↑
n
R2
R2+Rst
Tst’ Tst”
T
绕线式异步电动机的转 子串电阻起动，不仅限制起 动电流，同时增大起动转矩。 因此，绕线式异步电动机比 鼠笼式异步电动机的起动性 能好。
返回
三、反
转
正转 反转
三相异步电动机的转向决 定于旋转磁场的转向,而旋转 磁场的转向又与通入三相定子 绕组的电流相序有关, 因此, 改变相序即可改变转向。 只要将三相定子绕组接电源的 三根线中任意两根对调即可。
sm
1
U1 ’
电压不足，会造成电流增 s 大，电机发热。
返回
临界转差率sm与R2成正比。
最大转矩Tmax与R2无关。
R2’ < R2”
Tmax
T R2’ R2”
1
2. 机械特性 sm’ sm”
s
在电源电压U1不变时，电动机的转速n 和电 磁转矩T 间的关系称为电动机的机械特性。
返回
n = f (T) 机械特性曲线可由转矩特性曲线得来： n n > nm(AB段）： 为稳定工 n1 A 作区（s 较小），具有硬特 nN 性，即电动机具有自动适应 nm B 负载能力。 TL↑→T ＜TL→n ↓ →s ↑ →T ↑ → T =TL T
返回
定子接线端的连接
C A B
Z
W2 U1 V1
X
U2 W1
Y
V2
△接 接
返回
第二节 三相异步电动机的工作原理
旋转磁场
转动原理
转差率
返回
一、旋转磁场
1、旋转磁场的产生
定子三相绕组对称，且空间上互差120°， 接成形。 iA A U Y Y X W V Z iC C iB B

三相异步电动机的转矩

三相异步电动机的转矩

• 转矩T也与s有关。
由上式可见，转矩还与定子的相电压U1的平方成 正比。所以，电源电压的变动对转矩的影响很大。 转矩特性T =T(s)曲线如图 所示，当s很小时， T与s 成正比；当s很大时，T与 s 成反比(以双曲线为渐近 线)，并且有最大转矩Tmax 存在。
T
Tmax
0
n n0
sm
1 0
s
二、机械特性曲线
§5-4. 三相异步电动机的转矩 与机械特性
• 电磁转矩 T 是三相异步电动机最重要的物理量之一， 机械特性是电动机的主要特性。对电动机进行分析往 往离不开这两方面内容。
一、转矩公式
异步电动机的转矩是由旋转磁场每磁极的磁通 与 转子电流I2相互作用产生的。它应与电磁功率成正 比，因而与转子的功率因数有关。于是 T I 2 cos 2 K T I 2 cos 2
E1 U1 U1 4.44 f1 N1 4.Байду номын сангаас4 f1 N1
sE 20
2 R2 ( sX 20 ) 2
及 I2

s(4.44 f1 N 2 )
2 2 R2 X2
且 cos 2
R2
2 R2 ( sX 20 ) 2
则转矩公式可表示为
TK
2 sR2U1 2 R2 ( sX 20 ) 2
实际上，下图是通过上图右 旋90°得到的。
nN
b
T TN Tst Tmax
0
• 研究机械特性是分析为了分析电动机的运行性能。 在机械特性曲线上，要讨论三个转矩。
1. 额定转矩 TN 在电动机匀速转动时，其转矩T必须与阻力转矩TC 平衡，而阻力转矩包括负载转矩T2和空载损耗转矩 T0。一般T0很小，常可忽略，所以 n P2 a T T T T

异步电机机械特性 2

异步电机机械特性 2
异步电动机的启动转矩Tst与额定转矩TN之比用启动转矩 倍数kst来表示，即
Tst k st TN
5.1 三相异步电动机的机械特性
一般将异步电动机的特性曲线分为两部分：
转差率0～sm部分：在这一部分，T
s n
0
与s的关系近似成正比，即s增大时，T 也随之增大，该部分为异步电动机的
n1
sm
稳定运行区。
降压后同步转速n1不变； 降压后，最大转矩T随 U 12 成比
例下降，但是临界转差率sm不变；
降压后的启动转矩Tst也随 U 1 成
2
比例下降。
感应电动机降低电压时的人为机械特性
5.1 三相异步电动机的机械特性 2）定子回路串对称三相电抗器的人为机械特性
定子回路串电抗使sm和Tm都减小，机械特性的直线部分硬度也
加而增加（近似成正比）。
r2' 相对变小了， x x ' 开始成为分母中的主要部分，此 3、当s较大时， 1 2 s
时随着s的增大，电磁转矩T的增大并不是很大。
r2' r2' ' 4、当T达到最大值Tmax时，如果s再增大， 将更小，使得 远小于 x1 x 2 s s r2' ，此时 可略去不计，则电磁转矩T随s的增加而减小。 s
第5章
5.1
异步电动机的电力拖动
三相异步电动机的机械特性
5.1 三相异步电动机的机械特性
三相异步电动机的机械特性是指在电压和频率一定
情况下，转速n与电磁转矩T之间的关系，即n=f(T)。
由于异步电动机的转速n与转差率s之间存在着一定 的关系，所以异步电动机的机械特性通常也可用s=f(T)的 形式表示。 1、固有机械特性的分析 三相异步电动机的固有机械特性是指感应电动机工作在 额定电压和额定下，按规定的接线方式接线，定、转子外界

三相异步电动机的机械特性

三相异步电动机的机械特性

三相异步电动机的机械特性（一）机械特性方程1）物理表达式：T=CTФmI2’cosф2 (T是电磁作用的结果)2）参数表达式：3) 工程表达式：——外施电源电压；——电源频率；——电机定子绕组参数；——电机转子绕组参数。

（二）固有机械特性曲线1．形状(根据工程表达式来说明)AB段（s较大）：为双曲线，T与S成反比。

BO段(s很小)：为直线，T与S成正比。

向左转|向右转2．起动点A，n=0,S=1，起动转矩倍数KT=TS/TN 一般取0.8~1.83.临界点B临界转差率只与转子电阻有关. 取0.1~0.2最大转矩与电源电压UI2有关。

过载能力λ=Tm/TN取1.6~2.24.同步点On=n1 T=0 (理想的空载转速，旋转磁场的转速 )5.额定点C0< SN <Sm取0.02~0.06在该点附近有TN=9550PN/nN（三）人为机械特性1、降低定子电压的人为机械特性——“变瘦”当定子电压U1 降低时，电磁转矩T与U1 的平方成正比，故同步转速不变，Sm不变，最大转矩Tm 和起动转矩TS 随电压平方降低。

其特性曲线（红色）所示。

向左转|向右转2、转子串电阻的人为机械特性——“变软”当转子回路串电阻时，同步点不变，Sm与转子电阻成正比，转速随电阻增加而减小，最大转矩Tm保持不变，在一定范围内起动转矩有所增加，其特性曲线（红色）所示向左转|向右转3、降低定子电压频率的人为机械特性——“变小”降低定子电压频率时，同步转速随之下降，从而使得电机转速下降，但特性的硬度基本保持不变。

电动机在工作时要求主磁通保持不变，因此在降低频率的同时，定子电压也要随之降低。

向左转|向右转滑动轴承和滚动轴承的优缺点的比较时间：2012-07-25来源：阿里巴巴资讯摘要：现在市场上轴承越来越多，最常见的就是滚动轴承和滑动轴承，下面看一下两种轴承的比较.现在市场上轴承越来越多，最常见的就是滚动轴承和滑动轴承，下面看一下两种轴承的比较.滚动轴承是在滚动摩擦下工作的进口轴承。

三相异步电动机的电磁转矩和机械特性

三相异步电动机的电磁转矩和机械特性
智能化控制
利用先进的传感器、控制器和算法，实现三相异 步电动机的智能控制，提高电机响应速度和运行 稳定性。
集成化设计
将电机、减速器和控制器等部件集成在一起，形 成紧凑、高效的一体化系统，降低整体能耗和成 本。
面临的挑战与问题
效率与能耗
尽管三相异步电动机在许多领域已经取得了显著的节能效果，但在 高负载、高转速等极端工况下，仍存在较大的能耗和效率提升空间 。
电磁转矩的大小取决于定子电流的幅值、频率、电动机的磁路结构、转子电阻以 及气隙长度等因素。
电磁转矩的影响因素
定子电流
电源频率
定子电流的大小直接影响电磁转矩的大小 。随着电流幅值的增加，电磁转矩将增大 。
电源频率的变化也会影响电磁转矩的大小 。随着频率的升高，旋转磁场的转速增加 ，导致转子电流和电磁转矩的增大。
改变转差率调速
通过改变转差率的大小来调节 电动机的转速，实现有级调速 。
改变极对数调速
通过改变电动机的极对数来调 节转速，实现有级调速。
转子电阻调速
通过改变电动机转子电阻的大 小来调节转速，实现有级调速
。
控制策略与实现
矢量控制
通过控制电动机的励磁和转矩来实现 精确控制，常用在高性能的调速系统 中。
负载转矩
负载转矩的变化对电动机的转速和转矩也有显著 影响，负载增大，转速下降，转矩增大。
电机参数
电机的参数如电阻、电感等也会影响机械特性， 这些参数的变化会导致电动机性能的变化。
机械特性的应用场景
调速控制
通过改变电源电压或频率，可以实现对电动机转速的精确控制， 广泛应用于各种需要调速的场合。
负载匹配
三相异步电动机可以通过直接启 动、降压启动或软启动等方式启

电工技术：三相异步电动机的转矩与机械特性

电工技术：三相异步电动机的转矩与机械特性

二、机械特性
2.人为机械特性
人为地改变电动机地任一个参数（如U1、f1、p、定子回路电阻或电抗、转子 回路电阻或电抗)的机械特性称为人为机械特性。
R2 m1 p U s T 2 R2 ' 2 2f1 ( R1 ) ( X1 X 2 ) s
2 1
二、机械特性
一、电磁转矩
2.参数表达式
Pem T 1
2 m1 I 2
R2 2 R2 m1 pU1 S S 2 2f 1 R2 2 2f 1 R1 ＋ X 1 X 2 p S
T与电源参数（Ｕ1、f1）、结构参数（R、X、m、p）和运行参数（s）有关。 参数表达式用来分析或计算参数的变化对三相异步电动机运行性能的影响。
适用于绕线型异步电动机。
三相异步电动机的人为机械特性很多：
• 降低定子端电压的人为特性； • 改变转子回路的电阻的人为特性；
• 改变定转子回路电抗的人为特性；
• 改变极数后的人为特性； • 改变输入频率的人为特性等 一般重点研究降低定子端电压的人为特性和改变转子回路电阻的人为特性。
二、机械特性
（1） 降ቤተ መጻሕፍቲ ባይዱ时的人为机械特性
一、电磁转矩
3.实用表达式
2Tmax T S Sm Sm S
TN 9.55 PN nN
实用表达式应用于工程计算中。 通过铭牌数据求取电动机转矩的方法。
Tmax
PN mTN 9.55m nN
S m S N m 2 m 1


二、机械特性
电动机电磁转矩与转速之间的关系曲线，称为电动机的机械特性。
电压下降： • 理想空载速度不变； 定子电压 变化

第九章 三相异步电动机的机械特性及各种运转状态 第一节 三相异步电动机机械特性的三种表达式

第九章 三相异步电动机的机械特性及各种运转状态 第一节 三相异步电动机机械特性的三种表达式

U
2 X
(10 17)
R12
(X1
X
' 2
)
2
正号对应于电动机状态，而负号则适用于发电机状态 考虑 R1 << ( X1 + X2') ,可得：
Sm
R2'
X1
X
' 2
(10 18)
Tm
m1U
2 X
20 ( X1
X
' 2
)
(10 19)
可以看出：
4.几点规律
1)当电动机各参数及电源频率不变时， Tm 与 UX2 成正比，sm 因与 UX 无关而保持不变
二.异步电动机机械特性的参数表达式
采用参数表达式可直接建立异步电动机工作时转矩和转速关系并 进行定量分析
E
' 2
2f1W1kW1 m (10 5)
0
2f
p
(10 6)
T
m1 0
E
' 2
I
' 2
c
os
' 2
(10 7)
E
' 2
I
' 2
Z
' 2
(10 8)
R2'
c
os
' 2
PT
3I
2 2
R2 R f s
(10 44)
转子轴上机械功率为
P2 PT (1 s) (10 45)
s > 1，P2 为负值，即电动机由轴上输入机械功率 转子电路的损耗为
DP2 PT (1 s) (10 45)
DP2 数值上等于 PT 与 P2 之和，所以反接制动时能量损耗极大 3)用途 可以用于稳定下放位能性负载

三相异步电动机的转矩与机械特性

三相异步电动机的转矩与机械特性

三相异步电动机的转矩与机械特性电磁转矩是三相异步电动机最重要的物理量之一。

而机械特性是它的主要特性之一。

一、三相异步电动机的转矩三相异步电动机的电磁转矩为：将代入上式则有：二、三相异步电动机的机械特性1、*固有机械特性：异步电动机在额定电压和额定电流下，用规定的接线方式，定子电路和转子电路不串接任何电阻或电抗时的机械特性称为固有机械特性（自然机械特性）。

可用四个特征点来描述固有机械特性：1.当T=0点,即抱负空载点（0，n0 ）其中：n0=60f1/p2.电机额定工作点（TN,nN）其中：TN=9.55PN/nN3.启动点（Tst,0），此时n=0,s=1,所以有：4.极值点（nm,Tmax）有：电机固有机械特性的两个重要指标：(1) 启动力量系数(2) 过载力量系数转矩-转差率特性表达式：2、人为机械特性：转变定子电压、电子电流频率、定子电路串入电阻或电抗、转子电路串入电阻或电抗时的机械特性称为电动机的人为机械特性。

1）降电源电压时的人为机械特性当U降低，n0及Sm不变。

Tmax正比于U2。

即在同一转差率的状况下，人为特性与固有特性的转矩之比等于电压的平方和之比。

因此，异步电动机对电压的波动特别敏感。

此外，电网电压下降，在负载转矩不变的状况下，将使电动机转速下降，转差率S增加，电流增大，引起电机发热或烧坏。

2）定子电路串入电阻或电抗时的人为机械特性与降低电源电压时的人为特性类似，所不同的是定子电路串电阻或电抗的最大转矩比直接降压时的最大转矩大些。

3）定子电路串入电阻或电抗时的人为机械特性与降低电源电压时的人为特性类似，所不同的是定子电路串电阻或电抗的最大转矩比直接降压时的最大转矩大些。

Tmax正比于1/f2，Sm正比与1/f，n0正比与f，Tst正比与1/f。

注：转变频率时要保证最大转矩不变，应使U/f不变，因此变频时要转变电压。

曾成碧、赵莉华《电机学》书号ISBN978-7-111-25251-1ch10

曾成碧、赵莉华《电机学》书号ISBN978-7-111-25251-1ch10

Tmax
m1 pU12 1 = 2π f1 2C1 (r1 + r12 + ( x1 + x2 ) 2 ) ′
r2′ sk = xk

Tmax
m1 pU = 4π f1 xk
2 1
讨论: 讨论 （1）当电源频率和电机参数不变时，最大电磁转 ）当电源频率和电机参数不变时， 矩与电源电压的平方成正比； 矩与电源电压的平方成正比； （2）当电源电压和频率一定时，最大电磁转矩与 ）当电源电压和频率一定时， 短路电抗成反比； 短路电抗成反比； （3）最大电磁转矩与转子电阻无关，但临界转差 ）最大电磁转矩与转子电阻无关， 率与转子电阻有关，转子电阻增大， 率与转子电阻有关，转子电阻增大，临界转差率 增大， 曲线的最大值向 增大方向偏移。 曲线的最大值向s增大方向偏移 增大，T-s曲线的最大值向 增大方向偏移。
pm1 2 T= U1 r2′ 2 2π f1 2 ( ) + xk s
为异步电动机的短路电抗。 ′ xk = x1 + x2 ，为异步电动机的短路电抗。
r2′ s
2.机械特性 机械特性
当异步电动机电源电压恒定， 当异步电动机电源电压恒定，电机参数已知 可根据电磁转矩的参数表达式得到转差率s与 时，可根据电磁转矩的参数表达式得到转差率 与 电磁转矩T之间的关系曲线 之间的关系曲线， 曲线， 电磁转矩 之间的关系曲线，即 T = f (s) 曲线，称 为异步电动机的机械特性曲线。 为异步电动机的机械特性曲线。
Pm = Pem − pCu 2 1− s ′ = 3I 2 ( r2′) s
2
转子铜耗与电磁功率的关系： 转子铜耗与电磁功率的关系：pCu 2 = sPem 总机械功率与电磁功率的关系： 总机械功率与电磁功率的关系： m = (1 − s) Pem P

三相异步电动机的电磁转矩及机械特性

三相异步电动机的电磁转矩及机械特性

电动机起动时有最大转矩，可令sk=1 ，则起动 转矩为最大转矩时转子回路所串的电阻应为：
rs xk r2
16
1、三相绕线式异步电动机转子回路串电阻后，下 列参数将如何变化？ （1）起动电流 （2）起动转矩 （3）最大转矩 （4）临界转差率
减小，增大，不变，增大
17
2、若频率为50HZ的三相异步电动机接在频率为 60Hz的电网上运行，电动机下列参数将如何变化？ （1）起动转矩； （2）最大转矩； （3）起动电流。
最大电磁转矩与电源电压平方成正比；临界转差 率与电源电压无关。
转子回路电阻越大，临界转差率越大；最大电磁 转矩与转子电阻无关。
频率越高，最大电磁转矩和临界转差率越小；漏 抗越大，最大电磁转矩和临界转差率越小。
13
3.最大电磁转矩、起动转矩、额定转矩
Tmax
pm1
1
U12
1 2 xk
注意：
（1）三相异步机的 Tmax和电压的平方成正比，所
（2）最大电磁转矩 Tmax 最大转矩:电机带动最大负载的能力。
TL Tmax，电机因带不动负载而停转。
电磁转矩
r2
T
pm1
2 f1
U12
s ( r2)2
s
xk2
令 dT 0，求出当T最大时的转差率sK。
dS
10
3.最大电磁转矩、起动转矩、额定转矩
（2）最大电磁转矩 Tmax
sk
C1r2 r12 (x1 C1x2 )2
Tmax
m1 pU12
2 f1
2C1(r1
1 r12 (x1 x2 )2 )
sk
r2 xk
C1 1 Tmax
m1 pU12

第二节 三相异步电动机的电磁转矩和机械特性

第二节 三相异步电动机的电磁转矩和机械特性

第二节三相异步电动机的电磁转矩和机械特性三相异步电动机转轴上产生的电磁转矩是决定电动机输出的机械功率大小的一个重要因素，也是电动机的一个重要的性能指标。

一、三相异步电动机的转矩特性1、电磁转矩的物理表达式三相异步电动机的工作原理告诉我们，电磁转矩是旋转磁场与转子绕组中感应电流相互作用产生的，设旋转磁场每极的磁通量用Φ表示，它等于气隙中磁感应强度平均值与每极面积的乘积。

Φ表示了旋转磁场的强度。

设转子电流用I2表示。

根据电磁力定律，电磁转矩T em应与Φ成正比、与I2也成正比，即T em∝Φ·I2。

此外转子绕组是一个感性电路，转子电流I2滞后于感应电动势E2，它们之间的相位差角是。

考虑到电动机的电磁转矩对外做机械功，与有功功率相对应。

因此电磁转矩T em还与转子电路的功率因数cos有关，即与转子电流的有功分量I2cos(与E2同相位的电流分量)成正比。

总结以上分析，可列出异步电动机的电磁转矩方程式中KT是一个与电动机本身结构有关的系数。

该公式是分析异步电动机转矩特性的重要依据。

2、转矩特性电磁转矩与转差率之间的关系T em＝(S)称为电动机的转矩特性。

可以推得式中KT’、转子电阻R2、转子不动时的感抗X20都是常数，且X20远大于R2。

由于上式用电机定、转子绕组中的电阻、电抗等参数反映电磁转矩T em和转差率S之间的关系，所以上式又称之为电磁转矩的参数表达式。

由转矩的表达式(4-5)可知，转差率一定时，电磁转矩与外加电压的平方成正比，即T em∝U12。

因此，电源电压有效值的微小变动，将会引起转矩的很大变化。

当电源电压U1为定值时，电磁转矩T em是转差率S的单值函数。

图4-13画出了异步电动机的转矩特性曲线。

二、三相异步电动机的机械特性当电源电压U1和转子电路参数为定值时，转速n和电磁转矩T的关系n=f（T）称为三相异步电动机的机械特性。

机械特性曲线可直接从转矩特性曲线变换获得。

将图4-15中的转矩特性曲线顺时针转动90°，并将s换成n就可以得到三相异步电动机的机械特性曲线，如图4-16所示。

三相异步电动机的机械特性

三相异步电动机的机械特性

空载时损耗占比例大，效率低；随P2增 加，增加，当负载过大，铜损耗增加快，使 效率下降，如图所示。
2023年8月26日 星期六
§4－5 三相异步电动机的机械特性
效率曲线和功率因数曲线都是在额定负载附近 达到最高，因此合理选用电动机容量时，对电动 机的寿命、功率因数和效率都有很实际的意义。 5、功率因数特性cos1=f(P2)
§4－5 三相异步电动机的机械特性
本节要点： 一、三相异步电动机的工作特性 二、机械特性：n = f ( T ) ㈠固有机械特性曲线分析 ㈡人为机械特性 三、运行性能 1、运行状态 2、启动转矩倍数
3、过载能力 4、异步电动机机械特性的结论
2023年8月26日 星期六
§4－5 三相异步电动机的机械特性
原因：是静止的转子导体与定子旋转磁 场之间的相对切割速度很大（n1）。将 产生很大的I2，使定子电流也增大。但 由于转子绕组的功率因数cosφ2很小， 由于Tst=CTφI2cosφ2，故启动转矩并不 很大。
只有当Tst达到一定值时，电动机才 能启动。
Tst>TL ，将 S = 1代入T公式，即 可得Tst 的表达式。
2023年8月26日 星期六
§4－5 三相异步电动机的机械特性
⑵额定运行点（TN、nN） TN = 9.55 PN/nN
⑶临界工作点（Tm、nm） 当S = Sm 时，电磁转矩达到最大
值。
Sm ∈( 0.04，0.14 ) ⑷同步点（0、n1）
n = n1
2023年8月26日 星期六
§4－5 三相异步电动机的机械特性
2023年8月26日 星期六
§4－5 三相异步电动机的机械特性
2、转矩特性T=f(P2) 空载时P2=0，电磁转矩T等于空载转矩 T0。随着P2的增加，已知T2=9.55P2/n， 如n基本不变，则T2为过原点的直线。 考虑到P2增加时，n稍有降低，故 T2=f(P2)随着P2增加略向上偏离直线。 在T=T0+T2式中。T0很小，且为常数。所 以T=f(P2)将比平行上移T0数值，如图所 示。

三相异步电动机的机械特性

三相异步电动机的机械特性
结论：降低U1后的人为机械特性，仍然通过固有机械 特性的同步点，即：同步点保持不变。
1. 降低定子端电压U1的人为机械特性
2）最大转矩点
横坐标Tm ：
最大转矩Tm与定子端电压U1的 平方成正比，降低U1之后，最 大转矩Tm的值大幅度减小。
纵坐标nm： nm=n1(1-sm) =n1(1-R2/X2)
用平滑曲线连接这三个坐标 点，就得到了降低定子端电 压U1的人为机械特性。
1.降低定子端电压U1的人为机械特性
降低电压U1对电动机运行 性能的影响：
TL1 TL2
1）最大转矩Tm和启动转矩Tst 都大幅度减小，过载能力λ和 启动能力Kst都显著降低。 如果U1降低得太多，可能会因 为Tst<TL而无法启动，也可能 会因为Tm<TL而堵转。
长期欠压过载运行，电动机绕组的温升会超过允许值而损害 绕组的绝缘，甚至会烧毁绕组。
电动机的电气控制电路要设置欠电压保护：
1）电动机通常由接触器控制。接触器在其线圈电压下降到 85%UN时，会自动释放而切断电路，自带欠压保护功能。 2）低压断路器上有失压脱扣器，在低电压时会自动跳闸， 有欠压失压保护功能。 3）有时需要设置专门的欠电压继电器作欠压保护。
TL1 TL2 TL3
TL4
可采取的措施2：
电动机的固有机械特性
√ 换一台启动转矩Tst大于TL3，额定转矩TN与TL3相当的电动
机，带动TL3重新启动。
运行情况：
TN ≈ TL3，电动机会运行在额定状态附近，运行性能好。
★通过固有机械特性判断电机运行情况
参考答案4：
电动机带负载TL4不能启动， 绕组很快就会烧毁。
第1步： 从产品目录中查出电动机的外部参数值，计算出Tm和sm的 值，代入实用表达式，得到T = f ( s )。在转差率s的取值范 围内，计算出电动机若干个运行点的（s，T）坐标值。

三相异步电动机的电磁转矩与机械特性

三相异步电动机的电磁转矩与机械特性

图2-30 U1对机械特性的影响
❖ 阻转矩主要是轴上的机械负载转矩T2，此外，还包 括电动机的机械损耗转矩T0。若忽略很小的T0，则 阻转矩为
❖
TC=T2+T0≈T2
❖ 因此可近似认为，只要电动机的电磁转矩动机就可以等速运 行。
❖ 三个重要的转矩
❖ 1) 启动转矩Tst。电动机接通电源瞬间(n=0)的电磁 转矩Tst称为启动转矩。电动机的启动转矩必须大于 静止时其轴上的负载转矩才能启动。通常用Tst与TN 之比表示异步电动机的启动能力，则启动系数λst表 示为
三相异步电动机的电磁转矩与机械特性
❖ 电磁转矩是三相异步电动机的重要物理量，机械特 性则反映了一台电动机的运行性能。
❖ 1 电磁转矩
❖ 由三相异步电动机的转动原理可知，驱动电动机旋
转的电磁转矩是由转子导条中的电流I2与旋转磁场 每极磁通φ相互作用而产生的。因此，电磁转矩的 大小与I2及φ成正比。由于转子电路既有电阻，也有 感抗存在，故转子电流I2滞后于转子感应电动势E2 一个相位差角φ2，转子电路的功率因数为cosφ2。 因此异步电动机的电磁转矩与φ、I2、cosφ2成正比。
❖ TN=9550×55/1480=354.9 (N·m) ❖ Tst=λSTN=1.3×354.9=461 (N·m) ❖ Tm=λmTN=2.2×354.9=780 (N·m)
图2-28〓转矩特性曲线
❖ 2 机械特性
❖ 如果将图2-28的S坐标换成n坐标，将T轴右移到s=1 处，再将坐标顺时针旋转90°，便得到表示电动机 的转速n和电磁转矩T之间的关系n=f(T)的曲线，称 为电动机的机械特性曲线。如图2-29所示。
图2-29〓机械特性曲线
❖ 由于电动机的电磁转矩与定子相电压U1的平方成正 比，所以机械特性曲线将随U1的改变而变化，图230给出对应不同定子电压U1时的机械特性曲线。图 2-30中，U′1＜U1。由于U1的改变不影响同步转速n0， 所以两条曲线具有相同的n0。电动机的负载是其轴 上的阻转矩。电磁转矩T必须与阻转矩TC相平衡， 即T=TC时，电动机才能等速运行；当T＞TC时，电 动机加速；当T＜TC时，电动机减速。

三相异步电动机的机械特性

三相异步电动机的机械特性

三相异步电动机的机械特性
1.三相异步电动机的电磁转矩
三相异步电动机的转矩:
三相异步电动机的转矩是由旋转磁场的每极磁通Φ与转子电流I2相互作用而生成的。

它与Φ和I2 的乘积成正比，此外，它还与转子电路的功率因素cosφ2 有关。

转矩表达式：
式中，K——与电动机结构参数、电源频率有关的一个常数；
U1，U ——定子绕组相电压，电源相电压；
R2——转子每相绕组的电阻；
X20——电动机不动（n＝0）时转子每相绕组的感抗。

2.三相异步电动机的固有机械特性
固有机械特性：
异步电动机在额定电压和额定频率下，用规定的接线方式，定子和转子电路中的不串联任何电阻或电抗时的机械特性称为固有（自然）机械特性。

电动机的抱负空载转速：
额定转矩及额定转差率：S=(N1-N2)/N1
转矩－转差率特性的有用表达式，即规格化转矩－转差率特性。

3.三相异步电动机的人为机械特性
人为机械特性：
异步电动机的机械特性与电动机的参数有关，也与外加电源电压、电源频率有关，将关系式中的参数人为地加以转变而获得的特性称为异步电动机的人为机械特性。

电压U的变化对抱负空载转速no和临界转差率Sm不发生影响，但最大转矩Tmax与U2成正比，当降低定子电压时，no和Sm不变，而Tmax大大减小。

在同一转差率状况下，人为特性与固有特性的转矩之比等于电压的平方之比。

因此在绘制降低电压的人为特性时，是以固有特性为基础，在不同的S处，取固有特性上对应的转矩乘降低电压与额定电压比值的平方，即可作出人为特性曲线：
在电动机定子电路中外串电阻或电抗后，电动机端电压为电源电压减去定子外串电阻上或电抗上的压降，致使定子绕组相电压降低。

三相异步电动机的机械特性

三相异步电动机的机械特性




起动转矩与额定转矩的比值称为起动转矩倍 数或堵转转矩倍数，用kst表示，则有：

一般异步电动机起动转矩倍数为0.8～1.2。
Tst k st TN
r1sm 2 实用表达式： r 1 T 2 r1sm sm s Tm r22 r2 r22 2 s 2 2r1 2 s r2 s s s sm m

降电压人为机械特性曲线 Tm∝U12；Tst∝U12；n1和sm与电压无关
TL1-恒转矩负载特性、TL2-风机类负载特性
（2）定子回路串入对称电阻的人为机械特性

当定子电阻r1 增大时，同步 转速n1不变， 但临界转矩Tm、 临界转差率sm、 起动转矩Tst都 变小
定子回路串入对称电阻的 接线图和人为机械特性

从产品目录查出该异步电动机的数据PN、nN、 λm应用实用公式就可方便得出机械特性表达 式。
2.固有机械特性


异步电动机的固有机 械特性是指U1=U1N， ƒ1=ƒ1N，定子三相绕 组按规定方式连接， 定子和转子电路中不 外接任何元件时测得 的机械特性n =ƒ（T） 或T=ƒ（s）曲线。 对于同一台异步电动 机有正转（曲线1） 和反转（曲线2）两 条固有机械特性。
机械特性曲线

在电压、频率及绕组参数一定的条件下，电磁转矩T 与转差率s之间的关系可用曲线表示如图所示。
异步电动机机械特性
①最大转矩Tm

最大转矩Tm是T=ƒ（s）的极值点，最大转 矩为： 3 pU 2
Tm 4f1 r1 r12 ( x1 x2 ) 2

1


最大转矩对应的临界转差率为：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二节三相异步电动机的电磁转矩和机械特性
三相异步电动机转轴上产生的电磁转矩是决定电动机输出的机械功率大小的一个重要因素，也是电动机的一个重要的性能指标。

一、三相异步电动机的转矩特性
1、电磁转矩的物理表达式
三相异步电动机的工作原理告诉我们，电磁转矩是旋转磁场与转子绕组中感应电流相互作用产生的，设旋转磁场每极的磁通量用Φ表示，它等于气隙中磁感应强度平均值与每极面积的乘积。

Φ表示了旋转磁场的强度。

设转子电流用I2表示。

根据电磁力定律，电磁转矩T em应与Φ成正比、与I2也成正比，即T em∝Φ·I2。

此外转子绕组是一个感性电路，转子电流I2滞后于感应电动势E2，它们之间的相位差角是。

考虑到电动机的电磁转矩对外做机械功，与有功功率相对应。

因此电磁转矩T em还与转子电路的功率因数cos有关，即与转子电流的有功分量I2cos(与E2同相位的电流分量)成正比。

总结以上分析，可列出异步电动机的电磁转矩方程
式中KT是一个与电动机本身结构有关的系数。

该公式是分析异步电动机转矩特性的重要依据。

2、转矩特性
电磁转矩与转差率之间的关系T em＝(S)称为电动机的转矩特性。

可以推得
式中KT’、转子电阻R2、转子不动时的感抗X20都是常数，且X20远大于R2。

由于上式用电机定、转子绕组中的电阻、电抗等参数反映电磁转矩T em和转差率S之间的关系，所以上式又称之为电磁转矩的参数表达式。

由转矩的表达式(4-5)可知，转差率一定时，电磁转矩与外加电压的平方成正比，即T em∝U12。

因此，电源电压有效值的微小变动，将会引起转矩的很大变化。

当电源电压U1为定值时，电磁转矩T em是转差率S的单值函数。

图4-13画出了异步电动机的转矩特性曲线。

二、三相异步电动机的机械特性
当电源电压U1和转子电路参数为定值时，转速n和电磁转矩T的关系n=f（T）称为三相异步电动机的机械特性。

机械特性曲线可直接从转矩特性曲线变换获得。

将图4-15中的转矩特性曲线顺时针转动90°，并将s换成n就可以得到三相异步电动机的机械特性曲线，如图4-16所示。

1、四个工作点
在机械特性曲线中要抓住以下几个工作点。

●额定工作点C
三相异步电动机额定状态下运行，转速n=nN，s=sN，轴上的输出转矩即为带动轴上的额定机械负载的额定转矩TN，额定转矩TN为与额定功率PN和额定转速nN关系可用下式表示：
式中PN——电动机轴上输出的额定功率（kW）
nN——电动机额定转速（r/min）
TN——电动机上的输出的额定转矩（N?m）
在忽略电动机本身的机械损耗转矩（如轴承摩擦等）的情况下，可以认为电磁转矩TemN
与轴上的输出的额定转矩相等，经推导有
式中P2——电动机轴上输出的机械功率（kW）；
n——电动机转速（r/min）。

2）临界工作点B
从曲线中可以看出，曲线的形状以B点为界，AB段与BC段的变化趋势是完全不同的，B点就是一个临界点，并且B点对应的电磁转矩即为电机的最大转矩Tm，B点对应的转差率sm 为临界转差率。

可以证明，产生最大转矩时的临界转差率Sm为
从上两式可见，
●Tm与电源电压U1的平方成正比。

不同U1时的机械特性曲线如图4-15所示。

由图可见，对于同一负载转矩T2，当电源电压U1下降时，电动机转速也随之下降。

如果电源电压U1继续下降，使负载转矩T2超过电动机的最大转矩Tm时，电动机将停止转动，转速n=0。

这时电动机电流马上升高到额定电流的若干倍，电动机将因过热而烧毁，这种现象称为“闷车”或“堵转”。

●最大转矩Tm与转子电阻R2无关，但临界转差率Sm与转子电阻R2成正比。

改变R2能使Sm随之改变，例如增加R2，n＝( T em)曲线便向下移动(如图4-16)。

（3）为了保证电动机在电源电压发生波动时，仍能够可靠运行，一般规定最大转矩Tm 应为额定转矩TN的数倍，用λm表示，称为过载系数，即
（4-12）
过载系数λm表示了电动机允许的短时过载运行能力，是异步电动机的一个重要指标。

λm越大，电动机适应电源电压波动的能力和短时过载的能力就越强。

一般三相异步电动机的过载系数λm为1.8~2.5。

●起动工作点A
电动机起动瞬间，n= 0，s=1，所对应的电磁转矩Tst称为起动转矩。

Tst与电源电压U1的平方以及转子电阻R2成正比。

显然，只有在Tst大于负载转矩T2时，电动机才能起动。

Tst越大，电动机带负载起动的能力就越强，起动时间也越短。

Tst与TN的比值称为起动系数，用Kst表示，即
（4-13）
一般笼形转子异步电动机的Kst约为0.8~2。

由图4-16可见，改变转子电阻R2，可使起动转矩Tst=Tm，这在生产上具有实际的意义。

例如绕线转子异步电动机起动时，通过在转子电路中串入适当电阻，不仅可以减小转子电流，还可以起到增加起动转矩的作用。

●理想空载转速点D
曲线与纵坐标的交点即为理想空载转速点D，此时对应的n=n1为同步转速，s=0，电磁转矩T em=0。

但实际运行时，由于存在风阻、摩擦等损耗，所以实际转速略低于同步转速n1，故称D点为理想空载转速点。

2、稳定工作区与非稳定工作区
如图4-14所示，机械特性曲线可分为两部分：BD部分(0<S<Sm)称为稳定区，AB部分(S>Sm)称为不稳定区。

电动机稳定运转只限于曲线的BD段。

电动机在0<S<Sm区间运行时,只要负载阻转矩小于最大转矩Tm，当负载发生波动时,电磁转矩总能自动调整到与负载阻转矩相平衡，使转子适应负载的增减以稍低或稍高的转速继续稳定运转。

如果电动机在稳定运行中，负载阻转矩增加超过了最大转矩，电动机的运行状态将沿着机械特性曲线的BD部分下降越过B点而进入不稳定区，导致电动机停止运转。

因此,最大转矩又称崩溃转矩。

由机械曲线可推知：
（1）异步电动机稳定运行的条件是S<Sm，即转差率应低于临界转差率。

（2）如果从空载到满载时转速变化很小，就称该电动机具有硬机械特性。

上述表明，三相异步电动机具有硬机械特性。

（3）需要说明的是，上述负载是不随转速而变化的恒转矩负载，如机床刀架平移机构等，它不能在S〉Sm区域稳定运行；但风机类负载，因其转矩与转速的平方成正比，经分
析，可以在S〉Sm区域稳定运行。