博弈论与信息经济学 第三章 不完全信息静态博弈

海萨尼转换
海萨尼提出的处理不完全信息博弈的方法是，引入一个虚 拟的参与人——“自然”；自然首先行动决定参与人的特 征，参与人知道自己的特征，其他参与人不知道。 N
[p] 不进入 (0,300) 高 进入者 进入 合作 (40,50) 不进入
低
[1-p] 进入 在位者 合作 (30,80) 斗争 (-10,100)
i i的不确定性。我们用 G {A1 ,, An ; 1 ,, n ; p1 ,, pn ; u1 ,, un }
代表这个博弈。
不完全信息和贝叶斯纳什均衡
n 人不完全信息静态博弈的时间顺序为：
⑴自然给定类型向量 θ (1 ,, n ) ，其中， i i ，参与人 i 观 察到 i ，但参与人 j（ i ）只知道 p j (θ j | j ) ，观察不 到 i； ⑵参与人同时选择行动，参与人 i 从可行集 Ai ( i )中选择行 动 a i ，n 人的行动组合为 a (a1 ,, an )； ⑶参与人 i 的支付函数为 ui (ai , a i ; i ) 。 注意，在上面的定义中，虽然参与人 i 的类型是私人信息， 但是，行动空间和效用函数的结构是共同知识。换句话 说，尽管其他参与人并不知道参与人 i 的类型 i ，但是， 他们知道参与人 的行动空间和支付函数是如何依赖于 i i 参与人 的类型的。
ai (ci ) 是从 [c, c] 到{0，1}的一个函数，其中0表示不提供， i 1表示提供。参与人 的支付函数为：
ui (ai , a j , ci ) max(a1 , a2 ) ai ci
贝叶斯均衡是一组战略组合 ，使得对于每一 个 i 和每一个可能的 c i ，战略 ai (.)最大化参与人 i 的期望 效用函数 Ec j ui (ai , a ci , ci )。令 z j Pa j c j 1 为均衡状 j 态下参与人 j 提供的概率。最大化行为意味着，只有当参与 人 i 预期参与人 j 不提供时，参与人 i 才会考虑自己是否提 供。因为参与人 j 不提供的概率是 (1 z j ) ，参与人 i 提供的 i 预期收益是 1 (1 z j ) ，因此只有当 ci 1 z j 时，参与人 才会提供，即如果 ci 1 z j ， ai (ci ) 1 ； 如果 ci 1 z j ，ai (ci ) 0 。
贝叶斯均衡的应用举例
企业1：
L 低成本：q1{1 (q1 q 2 )} 1 H 高成本：q 2 {1 (q1 q 2 )} 1 1 L H E 1 q1{1 (q1 q 2 )} q1{1 (q1 q 2 )} 2 2 1 1 L 1 H 求导得：q1 (1 q 2 q 2 ) 2 2 2 1 L 11 H 5 代入，联合解得： 1 , q 2 q , q2 3 24 24
动有一致的信念，即都知道所有参与人类型的概率分布函 数 p1 ,..., n
。此即“海萨尼公理”。
海萨尼转换
用 θ i (1 ,, i 1 , i 1 ,, n ) 表示除 i 之外的所有参与人的类型组合。这 样， ( ,..., ) ( , ) 。 1 n i i 我们称 pi ( i i ) 为参与人 i 的条件概率，即给定参与人i 属于类型 的条件下，他有关其他参与人属于 θ i 的概率。根据条件概率规则，
1.不完全信息库诺特模型
已知：市场总供给 1 q 2，p a (q1 q 2 ) q 企业1：q1 0 1 q1 , q 2 q1 a (q1 q 2 ) c1 。其中c1 1 企业2：q 2 0 2 q1 , q 2 q 2 a (q1 q 2 ) c 2 。 3 L 低成本 c 2 4 1 有两个类型 概率 5 H 2 高成本 c 2 4 当a为2时，两个企业将如何决 策？
博弈论与信息经济学
——第三章 不完全信息静态博弈
不完全信息博弈
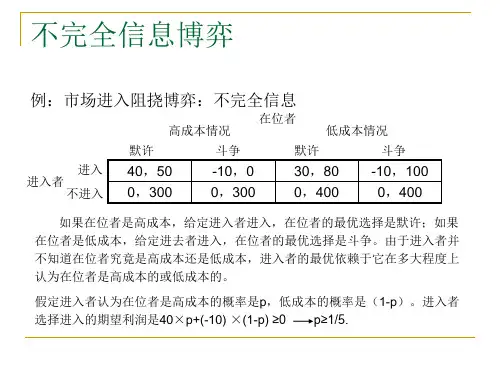
例：市场进入阻挠博弈：不完全信息
高成本情况 默许 进入者 进入 不进入 斗争 在位者 默许 低成本情况 斗争
40，50 0，300
-10，0 0，300
30，80 0，400
-10，100 0，400
如果在位者是高成本，给定进入者进入，在位者的最优选择是默许；如果 在位者是低成本，给定进去者进入，在位者的最优选择是斗争。由于进入者并 不知道在位者究竟是高成本还是低成本，进入者的最优依赖于它在多大程度上 认为在位者是高成本的或低成本的。 假定进入者认为在位者是高成本的概率是p，低成本的概率是（1-p）。进入者 选择进入的期望利润是40×p+(-10) ×(1-p) ≥0 p≥1/5.
在位者(0,400) 斗争 (-10,0)
上例市场进入阻挠博弈就可以转换为如图的完全但不完美信息博弈。 *完美信息博弈：如果博弈树的所有信息集都是为处理不完全信息博弈的标准方法。 将一个参与人所拥有的所有私人信息（即所有不是共同知识 的信息）被称为该参与人的类型。一般地，用 i 表示参 与人 i 的类型，它属于一个可能的类型集 i 。 类型依赖：每一个人的行动都依赖于它的类型。 通过海萨尼转换，博弈开始时，所有参与人对“自然”的行
贝叶斯均衡的应用举例
2.一阶招标拍卖 一级密封价格拍卖（the first-price sealed auction）是许 多拍卖方式中的一种。在这种拍卖中，投标人（bidders） 同时将自己的出价写下来装入一个信封，密封后交给拍卖 人，拍卖人打开信封，出价最高者是赢家(获得拍卖品)， 并按他的出价支付。这里，每个投标人的策略是根据自己 对物品的评价和对其他投标人评价的判断来选择自己的出 价，赢者的支付是他对物品的评价减去他的出价，其他投 标人的支付为零。
贝叶斯均衡的应用举例
首先考虑两个投标人的情况，i 1,2 。令 bi 0 是投标人i 的出价， v i 为拍卖品对投标人 i 的价值。假定 v i 只有 i 自己知道，因而 v i 是投标人 i 的类型，但两个投标人都 知道 v i 独立地取自定义在区间 [0, 1] 上的均匀分布函数。 投标人 i 的支付为

(a1 ., a2 .)
贝叶斯均衡的应用举例
ci 使得只有当 ci [c, ci ] 这就意味着，存在一个分割点 i 才会提供。类似的，存在一个 c j 使得只有当 时，参与人
c j [c, c ] 时，参与人 j 才会提供。 j
c
ci

c

ai (ci ) 1
不完全信息和贝叶斯纳什均衡
定义：在静态贝叶斯G {A1 ,, An ; 1 ,, n ; p1 ,, pn ; u1 ,, un } 博弈中， 纯策略贝叶斯纳什均衡是一个类型依存策略组 合a (θ) (a1 (1 ),, an ( n ))，其中，每个参与人 i 在给定自己的类 型 i 和其他参与人依存策略 a i (θ i ) 的情况下最大化自己的预期效用 函数 E θi ui 。换句话说，策略组合 a (θ) (a1 (1 ),, an ( n ))是一个 贝叶斯纳什均衡，如果对每一参与人i 及 i 的类型集 i 中的每一 i 个 i ，ai ( i ) 满足
i
p( i , i ) pi ( i i ) p( i )
i i
p( i , i ) p( i , i )
p( i )
p 这里， ( i ) 是边缘概率。如果类型的分布是独立的，pi ( i i )
不完全信息和贝叶斯纳什均衡
贝叶斯纳什均衡是完全信息静态博弈纳什均衡概念在不完 全信息静态博弈上的扩展。不完全信息静态博弈又称为静 态贝叶斯博弈。 ◆定义：n人静态贝叶斯博弈的战略式表述包括：参与人的类 型空间 1 ,, n，条件概率 p1 ,..., pn ，类型依存战略空间 A1 1 ,..., An n ，和类型依存支付函数u1 (a1 ,, an ;1 ),...,un (a1 ,, an ; n ) 参与人i知道自己的类型 i i ，条件概率 pi pi ( i i ) 描述 给定自己属于 i 的情况下，参与人i有关其他参与人类型
贝叶斯均衡的应用举例
假设：
1 ci [0,2], F (ci ) ci 2 1 1 2 c i 1 1 c i c i 2 2 3 2 1，ci 3 ai ci 2 0，ci 3
vi bi , 如果bi b j 1 u i (bi , b j ; vi ) 2 (vi bi ) , 如果bi b j 0, 如果bi b j
贝叶斯均衡的应用举例
现假设：bi vi ai ci vi 则：bi b j v j a j c j v j 又 vi [0,1] bi a j bi a j P i b j v j P v j b cj cj bi a j 1 u i (vi bi ) P i b j v j (vi bi ) P i b j v j (vi bi ) b b 2 cj 1 1 求导得：bi vi vi a j 2 2
ai (ci ) 0
ci 1 z j 1 P c j c j 1 F c j
同理：



c
a j (c j ) 1
c j
c j 1 F ci



c
a j (c j ) 0
由上两式可得：
ci 1 F 1 F ci


参与人2 提供 参与人1 提供 不提供 不提供
1-c1,1-c2 1,1-c2
1-c1,1 0,0
假定公共产品的好处（每人1单位）是共同知识，但每人的提供成本只有自己 知道（成本 c i 是参与人 i 的类型）。 c1和 c2 具有相同的、独立的定义在 [c, c] 上的分布函数，且是共同知识。