位置关系的相对性

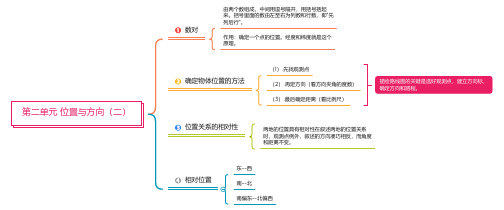
第二单元 位置与方向（二）
数
对 由
两个数组成，中间用逗号隔开，用括号括起
来。

括号里面的数由左至右为列数和行数，即“先
列后行”。

作
用：确定一个点的位置。

经度和纬度就是这个 原理。

确
定物体位置的方法 （1）.先找观测点 （2）.再定方向（看方向夹角的度数） （3）.最后确定距离（看比例尺）
描绘路线图的关键是选好观测点，建立方向标， 确定方向和路程。

位
置关系的相对性 两地的位置具有相对性在叙述两地的位置关系
时，观测点例外，叙述的方向凑巧相反，而角度 和距离不变。

相
对位置 东--西
南--北
南偏东--北偏西。

空间关系知识点总结一、空间概念空间是指周围的环境由物质实体所构成的三维空间。

在这个空间中，物体可以相对移动，相对位置也会发生变化。

在空间中，我们可以观察到物体的位置、形状和大小等属性。

空间关系是指事物在空间中的相对位置关系。

空间关系有三种形式，即相对位置、方位和距离。

1.相对位置：相对位置是指两个物体在空间中的相对位置关系。

当我们描述一个事物所处的位置时，一定要以另一事物为基准来描述，这就是相对位置。

例如，A在B的左边，B在A的右边，这是相对位置的描述。

2.方位：方位是指事物在空间中的朝向关系。

方位由四个基本方向组成，即东、西、南、北。

在地理空间中还有东北、东南、西北、西南等方位。

方位是空间中非常重要的关系，能够帮助我们更准确地描述事物在空间中的位置。

3.距离：距离是指两个事物在空间中的间隔距离。

在空间中，物体可以通过距离来描述物体的相对远近。

距离是空间关系中很重要的一个方面，它可以通过度量直线距离、曲线距离来描述物体之间的相对远近。

二、空间语言描述空间关系可以通过语言来进行描述。

语言描述可以帮助我们更加准确地了解物体在空间中的位置、方位以及距离。

在语言描述中，要注意以下几点：1.使用准确的定位词语：在描述空间关系时，要使用准确的定位词语，如“上、下、左、右、前、后”等。

这些词语可以帮助我们更加准确地描述事物在空间中的位置。

2.使用准确的方向词语：在描述方位时，要使用准确的方向词语，如“东、西、南、北”等。

这些词语可以帮助我们更加准确地描述事物在空间中的朝向关系。

3.使用准确的距离词语：在描述距离时，要使用准确的距离词语，如“远、近、远离、靠近”等。

这些词语可以帮助我们更加准确地描述事物在空间中的相对远近关系。

三、空间关系的认知发展儿童对空间关系的认知发展是一个渐进的过程。

在儿童的认知过程中，从最初的“具体视觉参照”到“图形概念”再到“抽象概念”，儿童对空间关系的认知逐渐升级。

1.具体视觉参照：儿童最开始的认知是基于具体的物体进行的。

六年级数学重点内容及易错题(上册)第一单元分数乘法一、分数乘法(一)分数乘法的意义：1、分数乘整数与整数乘法的意义相同。

都是求几个相同加数的和的简便运算。

例如：65×5表示求5个65的和是多少? 1/3×5表示求5个1/3的和是多少?2、一个数乘分数的意义是求一个数的几分之几是多少。

例如：1/3×4/7表示求1/3的4/7是多少。

4×3/8表示求4的3/8是多少.(二)、分数乘法的计算法则：1、分数与整数相乘：分子与整数相乘的积做分子，分母不变。

(整数和分母约分)2、分数与分数相乘：用分子相乘的积做分子，分母相乘的积做分母。

注意：当带分数进行乘法计算时，要先把带分数化成假分数再进行计算。

3、为了计算简便，能约分的要先约分，再计算。

（尽量约分，不会约分的就不约，常考的质因数有11×11=121；13×13=169；17×17=289；19×19=361）4、小数乘分数，可以先把小数化为分数，也可以把分数化成小数再计算（建议把小数化分数再计算）。

(三)、乘法中比较大小的规律一个数(0除外)乘大于1的数，积大于这个数。

一个数(0除外)乘小于1的数(0除外)，积小于这个数。

一个数(0除外)乘1，积等于这个数。

(四)、分数混合运算的运算顺序和整数的运算顺序相同。

整数乘法的交换律、结合律和分配律，对于分数乘法也同样适用。

乘法交换律： a × b = b × a乘法结合律：( a × b )×c = a × ( b × c )乘法分配律：( a + b )×c = a c + b c二、分数乘法的解决问题(已知单位“1”的量(用乘法)，即求单位“1”的几分之几是多少)1、画线段图：(1)两个量的关系：画两条线段图，先画单位一的量，注意两条线段的左边要对齐。

(2)部分和整体的关系：画一条线段图。

位置与方向相对性《位置的相对性》教学设计教学内容：新课标人教版第四册下第二单元《位置与方向》p22例3、做一做及p24练习四1、2题。

教学目标：知识与技能：使学生在学会确定任意方向的基础上，进一步体会位置关系的相对性过程与方法：并使学生在积极探索与交流的过程中进一步发展空间观念。

情感态度价值观：培养学生勇于探索、实践的学习精神。

教学重点：体会位置关系的相对性教学难点：现实生活中位置关系的相对性教学过程：一、自主学习1、同组同学互相说道：张三在李四的边，李四在张三的边。

教师：为什么同学们相互叙述对方的边线不一样？生：东和西、南和北的位置不是固定不变的，是相对而言的。

【设计意图】通过这一小游戏使学生自己辨认出：观测点出现了发生改变，对边线关系的叙述也随之发生改变了，这样的设计能够训练学生擅于从平时的生活中辨认出问题，并且自己谋求解决问题的方法和途径，培育积极探索精神。

通过游戏，同学们得出了左右相对而言的道理，那么我们这几天一直在研究的物体的位置会是什么样子的呢？2、写作并独立自主顺利完成教材p22基准3及搞一搞(1)上海在北京的南偏东约30°的方向上，距离约1067千米。

北京在上海的约°的方向上，距离约千米。

(2）做一做3、4、问题：（1）我们描述的沈阳和北京两个城市的位置关系和两位同学的位置关系为什么会出现两种不同的方式呢？（2）恳请同学们观测我们记录的两个城市之间的边线关系以及两位同学间的边线关系，你能够辨认出他们在方向、角度和距离上分别存有什么关系？二、交流展示1、小组内交流，合作自学，亲身经历解决问题的过程2、全班交流首先学生汇报自主学习2、3题的学习结果。

然后在些基础上交流第4题的结论。

在交流中引导学生明确：由于所选观测点不同，所在在描述两物体的位置关系时也存在着相对性；两物体的位置关系是“方向相对，偏角相同，距离相等”。

3、检验地图上两个城市之间的边线关系的相对性（1）请同学们，观察测量一下北京和沈阳之间的位置关系，它们之间的位置关系是不是也具有这样的性质？（2）辨认出了两物体之间边线关系的相对性，能够帮忙我们化解什么问题？生：我测量出了其中的一个，例如：北京在上海的北偏西约30°的方向上，利用相对性就得出了上海在北京的南偏东约30°的方向上师：除了谁也就是这么搞的？谁就是两个都测量出的？结果一样吗？三、测评反馈1、课本p24练习四第1题2、（1）小芳家在学校的偏约°的方向上，距离约米。

《位置的相对性》教学设计教学内容：新课标人教版第四册下第二单元《位置与方向》P22例3、做一做及P24练习四1、2题。

教学目标：知识与技能：使学生在学会确定任意方向的基础上，进一步体会位置关系的相对性过程与方法：使学生在探索与交流的过程中进一步发展空间观念。

情感态度价值观：培养学生勇于探索、实践的学习精神。

教学重点：体会位置关系的相对性教学难点：现实生活中位置关系的相对性教学过程：一、自主学习1、同组同学互相说：张三在李四的边，李四在张三的边。

教师：为什么同学们相互描述对方的位置不一样？生：东和西、南和北的位置不是固定不变的，是相对而言的。

【设计意图】通过这一小游戏让学生自己发现：观测点发生了改变，对位置关系的描述也随之改变了，这样的设计能训练学生善于从平常的生活中发现问题，并且自己寻求解决问题的方法和途径，培养探索精神。

通过游戏，同学们得出了左右相对而言的道理，那么我们这几天一直在研究的物体的位置会是什么样子的呢？2、阅读并自主完成教材P22例3及做一做(1)上海在北京的南偏东约30°的方向上，距离约1067千米。

北京在上海的约°的方向上，距离约千米。

(2）做一做3、4、问题：（1）我们描述的沈阳和北京两个城市的位置关系和两位同学的位置关系为什么会出现两种不同的方式呢？（2）请同学们观察我们记录的两个城市之间的位置关系以及两位同学间的位置关系，你能发现他们在方向、角度和距离上分别有什么关系？二、交流展示1、小组内交流，合作学习，亲身经历解决问题的过程2、全班交流首先学生汇报自主学习2、3题的学习结果。

然后在些基础上交流第4题的结论。

在交流中引导学生明确：由于所选观测点不同，所在在描述两物体的位置关系时也存在着相对性；两物体的位置关系是“方向相对，偏角相同，距离相等”。

3、验证地图上两个城市之间的位置关系的相对性（1）请同学们，观察测量一下北京和沈阳之间的位置关系，它们之间的位置关系是不是也具有这样的性质？（2）发现了两物体之间位置关系的相对性，能帮我们解决什么问题？生：我测量出了其中的一个，例如：北京在上海的北偏西约30°的方向上，利用相对性就得出了上海在北京的南偏东约30°的方向上师：还有谁也是这么做的？谁是两个都测量出来的？结果一样吗？三、测评反馈1、课本P24练习四第1题2、（1）小芳家在学校的偏约°的方向上，距离约米。

六年级下册数学知识点总结 基础数学的知识与运⽤是个⼈与团体⽣活中不可或缺的⼀部分.其基本概念的精炼早在古埃及、美索不达⽶亚及古印度内的古代数学⽂本内便可观见。

下⾯店铺整理了⼀些关于六年级下册数学知识点总结，欢迎⼤家参考! 第⼀单元分数乘法 ⼀、分数乘法 (⼀)分数乘法的意义： 1、分数乘整数与整数乘法的意义相同。

都是求⼏个相同加数的和的简便运算。

例如：65×5表⽰求5个65的和是多少? 1/3×5表⽰求5个1/3的和是多少? 2、⼀个数乘分数的意义是求⼀个数的⼏分之⼏是多少。

例如：1/3×4/7表⽰求1/3的4/7是多少。

4×3/8表⽰求4的3/8是多少. (⼆)、分数乘法的计算法则： 1、分数与整数相乘：分⼦与整数相乘的积做分⼦，分母不变。

(整数和分母约分) 2、分数与分数相乘：⽤分⼦相乘的积做分⼦，分母相乘的积做分母。

注意：当带分数进⾏乘法计算时，要先把带分数化成假分数再进⾏计算。

3、为了计算简便，能约分的要先约分，再计算。

(尽量约分，不会约分的就不约，常考的质因数有11×11=121;13×13=169;17×17=289;19×19=361) 4、⼩数乘分数，可以先把⼩数化为分数，也可以把分数化成⼩数再计算(建议把⼩数化分数再计算)。

(三)、乘法中⽐较⼤⼩的规律 ⼀个数(0除外)乘⼤于1的数，积⼤于这个数。

⼀个数(0除外)乘⼩于1的数(0除外)，积⼩于这个数。

⼀个数(0除外)乘1，积等于这个数。

(四)、分数混合运算的运算顺序和整数的运算顺序相同。

整数乘法的交换律、结合律和分配律，对于分数乘法也同样适⽤。

乘法交换律： a × b = b × a 乘法结合律： ( a × b )×c = a × ( b × c ) 乘法分配律： ( a + b )×c = a c + b c ⼆、分数乘法的解决问题(已知单位“1”的量(⽤乘法)，即求单位“1”的⼏分之⼏是多少) 1、画线段图：(1)两个量的关系：画两条线段图，先画单位⼀的量，注意两条线段的左边要对齐。

位置的相对关系学会描述物体的位置关系物体的位置关系是描述物体在空间中相对位置的一种方式，它能够准确传达物体之间的相对位置，为我们理解和描述环境中的事物提供了基础。

掌握位置的相对关系不仅在日常生活中有着广泛的应用，也是科学研究和技术应用的基础。

本文将介绍一些常见的描述物体位置关系的方法和技巧。

一、方位词描述位置关系方位词是描述物体位置关系最常用的工具之一。

方位词可以帮助我们准确地描述物体在空间中的位置，指明它们之间的相对关系。

常见的方位词有：上、下、左、右、前、后、内、外等。

例如，我们可以说：“杯子在桌子上。

”这句话用方位词“上”指明了杯子与桌子的位置关系。

同样，我们可以说：“书放在书架的左边。

”通过方位词“左边”，我们清楚地描述了书与书架之间的位置关系。

二、距离和方向描述位置关系除了方位词，距离和方向也是描述物体位置关系的重要因素。

距离可以用来表示物体之间的远近关系，而方向可以指示物体之间相对位置的朝向。

在描述距离时，我们可以使用数字、单位和比较级词语来量化。

例如，“这两个建筑物相距500米。

”或者“机场离市区比较远。

”在描述方向时，可以使用方位词、指示词和动词短语等。

例如，“从北向南走”或者“朝右边拐”。

三、图形和示意图描述位置关系图形和示意图是更直观地描述物体位置关系的方法。

通过绘制物体的简图或者示意图，我们可以更加清楚地展示物体之间的相对位置。

在图形和示意图上，可以使用箭头、线段和标记等来表示物体的位置和方向。

这种方法常用于地图、平面图、拓扑图等领域。

四、应用举例位置的相对关系在各行各业都有广泛的应用。

以下是一些实际应用举例：1. 导航系统：利用位置的相对关系，导航系统能够准确地指引我们的行进方向，并帮助我们到达目的地。

2. 建筑设计：在建筑设计中，需要准确描述建筑物之间的相对位置和布局，这样才能保证建筑物的合理布局和空间利用。

3. 调度管理：在物流和交通领域，位置的相对关系是调度管理的基础。