平面类问题有限元分析

8.3.4
创建实体模型
拾 取 菜 单 Main Menu → Preprocessor → Modeling → Create → Areas → Circle → By Dimensions。弹出如图 8-8 所示的对话框，在“RAD1” 、 “RAD2” 、 “THETA2”文本框中分 别输入 0.1、0.05 和 90，单击“OK”按钮。 77
第8例
平面问题的求解实例——厚壁圆筒问题
“Item, Comp”两个列表中分别选“Stress” 、 “Y-direction SY” ，单击“OK”按钮。 注意：该路径上各节点 X、Y 方向上的应力即径向应力r 和切向应力t。
图 8-15
映射数据对话框
8.3.12
作路径图
拾取菜单 Main Menu→General Postproc→Path Operations→Plot Path Item→On Graph。弹 出如图 8-16 所示的对话框，在列表中选“SR” 、 “ST” ，单击“OK”按钮。
8.3.6
施加约束
拾取菜单 Main Menu→Solution→Define Loads→Apply→Structural→Displacement→On Lines。弹出拾取窗口，拾取面的水平直线边，单击“OK”按钮，弹出如图 8-11 所示的对话 框，在列表中选择“ UY ” ，单击“ Apply”按钮，再次弹出拾取窗口，拾取面的垂直直线 边，单击“OK”按钮，在图 8-11 所示对话框的列表中选择“UX” ，单击“OK”按钮。
76
第8例
平面问题的求解实例——厚壁圆筒问题
图 8-3 单元类型对话框
图 8-4
单元类型库对话框
图 8-5

* 1 1 * 2 * 3 3
* T
F
T
* * * * * x x y * * y z z xy xy yz yz zx zx
({ } )
T
e T
R
e
(f)
而单元内的应力在虚应变上所做的功为
tdxdy
(g)
这里我们假定单元的厚度t为常量。把（d）式及（4-16） 式代入上式，并将提到积分号的前面，则有
({ } )
e T
B D B
T
e
tdxdy
根据虚位移原理，由（f）和（h）式可得到单元的虚功方程 即 e T e e T e T ({ } ) R ({ } ) B D B tdxdy 注意到虚位移是任意的，所以等式两边与相乘的项应该相等， 即得
R
e
B D Btdxdy
T
e
记
k B D B tdxdy
e T
(4-24) (4-25)
则有
R k
e e
e
上式就是表征单元的节点力和节点位移之间关系的刚 度方程，[k]e就是单元刚度矩阵。如果单元的材料是均质的 ，那么矩阵 [D] 中的元素就是常量，并且对于三角形常应 变单元，[B]矩阵中的元素也是常量。当单元的厚度也是常 量时,因 dxdy ,所以式(4-24)可简写为
1 2 4 7 11 3 5 8 6 9 10 15
12
13
14
图 4-6 a
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 15
2
3
4
5

分析与决策
(1)何种类型？
平面问题中的结构问题，且为静力问题；
平面问题中具有对称性，为减少[K]，简化模型取
1/4；
简化后加约束，（1）在ox面上，位移u是对称的，
位移v是反对称的；在oy面上，位移u是反对称的， 位移v是对称的； （2）在ox面上，载荷对称，在oy 面上，载荷对称；
(1)何种类型？

4.5剖分面（续）
以垂线剖分面。依次单击preprocessor-modelingoperate-booleans-divide-area by line，弹出对话框， 选择对话框中的box单选，用窗口选择两个面元素， 后单击apply,在窗口中选L6-ok,完成面元素剖分。 单击plotctrls菜单中的numbering命令，关闭line numbers –ok; 单击plot菜单中的area命令，用面元素显示模型， 剖分的模型如图所示，由2个面变为4个面，面元素 的编号同时发生变化。
Preprocessor-material
props-material models-弹出define material model behavior 对话框-列表框material models available中， 依次单击structural-linear-elastic-isotropic， 添加弹性模量2.1e+11，泊松比0.3-ok;

操作过程
一、建立新文件
二、类型的选择 Structural-ok；
二、前处理
1、添加单元类型 选择：Quad 4node 42(单元库编号)； 具有厚度：选择 option-plane str w/thk(平面应力有厚度)；
2、设置实常数（Real constants）

Re=
NT
s
Pstds
江西五十铃发动机有限公司
技术中心 12 /33
4、整体分析 整体刚度矩阵 整体刚度矩阵组装的基本步骤：
先求出各个单元的单元刚度矩阵； 将单元刚度矩阵中的每个子块放在整体刚度矩阵中的对应位置上，得到单 元的扩大刚度矩阵； 将全部单元的扩大矩阵相加得到整体刚度矩阵。
不失一般性，仅考虑模型中有四个单元，如图所示，四个单元的整体节点位 移列阵为
τZX z= + t/2 =0
因板很薄，载荷又不沿厚度变化，应力沿板 的厚度方向是连续分布的，可以认为，在整
Z
个板内各点都有
σZ=0 τYZ=0 τZX=0
O
tX
图1 平面应力问题
根据剪应力的互等性、物理方程，可得描述平面应力问题的八个独立的基本变量 为
江西五十铃发动机有限公司
技术中心 4 /33
σ=[σX σY τXY]T ε=[εX εY γXY]T
x2 y2 ɑ1= x 3 y 3
1 y2 b1=- 1 y 3
1 c1= 1
x2 x3
(1,2,3)
上式表示下标轮换，即1 2，2 3，3 1同时更换。
江西五十铃发动机有限公司
技术中心 9 /33
重写位移函数，并以节点位移的形式进行表达，有
uv((xx,,yy))N（x,y）qe
其中形函数矩阵为
Y
江西五十铃发动机有限公司
图2 平面应变问题
技术中心 5 /33
根据几何方程、物理方程可得，描述平面应变问题的独立变量也是八个，且与 平面应力问题的一样。只是弹性矩阵变为
1
D=
E1
1 1 2 1
1

19
4）形函数的性质
形函数是有限单元法中的一个重要函数，它具 有以下性质： 性质1 形函数Ni在节点i上的值等于1，在其它节点 上的值等于0。对于本单元，有
20
Ni ( xi , yi ) 1 Ni ( x j , y j ) 0 Ni ( xm , ym ) 0
（i、j、m）
利用 N i 1 (ai bi x ci y )和ai、bi、ci公式证明 2A
对于一个具体问题进行分析，不管采用什么样的单元， 分析过程与思路是一样的，所不同的只是各种单元的位移模 式和单元刚度矩阵不一样，其他的包括整体刚度矩阵的组装 过程都完全一样，所以我们仅仅对矩形单元位移模式的求取 和单元刚度矩阵的求解加以介绍。
4.7 收敛准则
可以证明，对于一个给定的位移模式，其刚度系统的数 值要比精确值大。所以，在给定载荷的作用下，有限元计算 模型的变形要比实际结构的变形小。因而，当单元网格分得 越来越细时，位移的近似解将由下方收敛于精确解，即得到 真实解的下界。 为了保证解答的收敛性，要求选取的位移模式必须满足 以下三个条件： 1）位移模式必须包含单元的刚体位移 也就是说，当节点位移是某个刚体位移所引起时，弹 性体内将不会产生应变。所以位移模式不但要具有描述单元 本身形变的能力，而且还要具有描述由其他变形而通过节点 位移引起单元刚体位移的能力。例如，三角形三节点位移模 式中，常数项就是用于提供刚体位移的。
Ni(x、y)
1 i(xi，yi) x xi
x xi N i ( x, y ) 1 x j xi
N m ( x, y ) 0
证
N
y j (xj，yj)
m (xm，ym)
xj
x
N i ( x, y )

1 x y x x y 1 E 1 2 1 y x y y x y E 1 E
1 2 x E
xy
2(1 ) xy E
23
位移模式的收敛性分析
（2）位移模式必须包含单元的刚体位移
单元位移一般包括两部分
• 本单元变形引起的位移 • 其他单元变形引起的位移-----刚体位移 刚体位移：指应变分量εx, εy 和γxy=0时的位移
3 3 u 1 2 x 3 y 1 2 x 5 y 5 y 2 2 3 3 v 4 5 x 6 y 4 6 y 5 x 5 x 2 2
换成 1 即可。

E 1 2
返 回 章 节 目 录 ，
1 E (1 u ) D (1 )(1 2 ) 1 0

1 1 0
0 1 2 2(1 ) 0
12
第四章 平面结构问题的有限单元法
其中， 是三角形单元的面积，当三角形单元结 点i、j、m按逆时针次序排列时，则有 1 1 1 ( xi y j x j y m x m y i ) ( x j y i x m y j xi y m ) 2 2 2
19
第四章 平面结构问题的有限单元法
x j ym x m y xm y m 1 yj bi y j ym 1 ym 1 xj ci xm x j 1 xm ai xj yj
22
位移模式的收敛性分析
（1）位移模式必须包含单元的常应变状态

4.1 三角形常应变单元
（1）单元特性分析 1）用面积坐标建立单元位移场——面积坐标的定义
Ai Apjm Aj Apmi Ak Apij
恒等关系：
A Ai Aj Am Aijm
P点位置可由3个比值来确定：
p(Li , Lj , Lm )
其中面积坐标：
Li Ai / A Lj Aj / A Lm Am / A
4)：单元推导。 对单元构造一个适合的近似解，即推导有限单元的列式，其中
包括选择合理的单元坐标系，建立单元试函数，以某种方法给出单元 各状态变量的离散关系，从而形成单元矩阵(结构力学中称刚度阵或 柔度阵)。
对工程应用而言，重要的是应注意每一种单元的解题性能与约
束。 5)总装集成。 将单元总装形成离散域的总矩阵方程(联合方程组)，反映对近似
0
Nm
Ni
I22
单元内任意一点的位移可由节点位移表示为：
N j I22
d
u
v
Nδe
e ui vi u j v j um
Nm I22
T
vm
4.1 三角形常应变单元
（1）单元特性分析
2）单元应变和单元应力
d
u
v
Nδe
代入
ε
x y
u / x v / y
xy
u / y v / x
其中
K rs
BrT DBshA
Eh
4(1 2 ) A
brbs
1
2
crcs
crbs
1
2
brcs
brcs
1
2
crbs
crcs
1
2
brbs
4.1 三角形常应变单元

ANSYS提供了轴对称模型和计算结果旋转扩展功能，使 用户仅仅计算截面结果就可以获得部分或全部模型及其 结果显示。
Utility Menu>Plotctrls>Style>Symmetry Expansion>2D Axis-Symmetric Expansion
5.3 具有对称性结构的分析
几何建模
1. 生成矩形：Main Menu>Preprocessor>Modeling> Create >Areas>Rectangle>By 2 Corners，输入：X=0，Y=0，Width=0.04，Heighth=0.075，单击Apply按钮。再输 入：X=0，Y=0.015，Width=0.025，Heighth=0.012，单击OK按钮。
第5章 平面问题和轴对称问题的有限元法
5.1 平面问题基本知识 5.2 轴对称问题基本知识 5.3 具有对称性结构的分析 5.4 练习题
5.1 平面问题基本知识
• 一、平面应变问题
1. 特点： 1) z向尺寸远大于x，y向尺寸，且与z轴垂直的各个横 截面尺寸都相同。 2) 受有平行于横截面（x、y平面）且不沿z向变化的 外载荷（包括体力x、y，但z=0），约束条件沿z向 也不变。即，所有内在因素和外来作用都不沿长度 变化。 y
P
x
受内压的圆柱管道
长水平巷道等
5.1 平面问题基本知识
• 一、平面应变问题 • 在ANSYS中，总是将几何尺寸很大的方向制定为
总体坐标系的Z方向，模型需要在总体坐标系的 XOY平面内建立模型，这时Z方向的应变为0，但 存在应力；
• 常用结构单元类型有：plane42、 plane82、 plane182、 plane183等，设置单元KEYOPT(3) 为Plane strain.

1
6
P
3
4 5
4
2
位移协调条件：各单元共享节点的位移相等 节点平衡条件：各节点单元内力与节点外力构成平衡力系
最终数学模型： K Q
基本概念
单元（element） 节点 (node)
回顾
单元节点位移 (node displacement)
单元节点内力 (node force)
单元刚度矩阵 (element stiffness matrix)
e
bx u by v
d
S
e p
px u py v dS
代入
u v



N

e
{} [B]{ }e
{ } [S]{ }e
得
内力虚功＝
e x x y y xy xy d
T d
cj
y)v j

(am
bmx

cm y)vm ]
二、平面问题三角形单元分析
三角形单元形函数
形函数
u x,
y

1 2A
[(ai

bi x

ci
y)ui

(a j

bj x

cj
y)u j

(am

bm x

cm
y)um ]
v x,
y

1 2A
[(ai

bi x

ci
y)vi

(a j

插值系数的确定：待定系数法
ui a1 a2 xi a3 yi u j a1 a2 x j a3 y j um a1 a2 xm a3 ym

2.FEM分析的主要步骤：
1.将连续体变换为离散化结构 2.对单元进行分析 位移模式 应变列阵 应力列阵
结点力列阵 等效结点荷载列阵 3.整体分析
§6-3 单元的位移模式与解答的收敛性
e T
位移模式 三角形单元
FEM是取结点位移δi 为基本未知数的。问题是如何求 应变、应力。
( δ 来求出单元 首先,必须解决由单元的结点位移 δ i δ j δ m T d ((, u xy ) v (, xy ) 。 的位移函数 e 该插值公式表示了单 δ 应用插值公式,可由 求出位移 d 。 元中位移的分布形式,因此称为位移模式。 在结点三角形单元中,可以假定位移分量只是坐标的线性 函数,也就是假定：
FEM的分析过程(2) 2.单元分析
求解方法
每个三角形单元仍然假定为连续的、均匀的、各向同 性的完全弹性体。因单元内部仍是连续体，应按弹性力学 方法进行分析。 T 取各结点位移 δ 为基本未知量，然后 ( uv ) ( i 1 , 2 , ) i i i 对每个单元,分别求出各物理量,并均用 δ i 1 ,2 , )来表示。 i( 单元分析的主要内容： (1)应用插值公式, 由单元结点位移
e T δ ( δ δ δ ) i j m 求单元的位移函数
,
T d ((, u xyvxy ) , (, ) ) .
该插值公式称为单元的位移模式,记为 d Νδe .
(2)应用几何方程,由单元的位移函数d,求出单元的应变 ε Bδe .
FEM的分析过程(2) 2.单元分析
单元分析的主要内容： (1)应用插值公式, 由单元结点位移
FEM的分析过程(3) 3.整体分析
求解方法
作用于结点i上的力有：

由以上分析可知，在划分单元时，只需确定单元节点的整 体坐标值，而不必画出等参元的具体形状，因为在计算中实际 使用的只有单元四个节点在整体坐标系下的位移值。
等参元变换的条件为 J ≠ 0 ，因此在有限元网格划分时，要 特别注意这一点。
等参单元等效节点力（4节点）
（1）集中力引起的单元节点载荷
单元内某点受到集中载荷P=[Px Py]T，移置到单元节 点上的等效节点力为：
j
同理 得
dη = ∂x dηi + ∂y dη j
∂η
∂η
∂x dξ
dA =
dξ × dη
=
∂ξ
∂x
dη
∂µ
∂y dξ ∂x
∂ξ
∂y
dη
=
∂ξ
∂x
∂η ∂µ
∂y
∂ξ
∂y
dξdη
∂η
等参单元刚度（4节点）
因为
∂x ∂y
J
=
∂ξ
∂x
∂ξ
∂y
∂η ∂η
雅可比行列式 Jacobi
曲边面积元dA:
dA = J dξdη
8 平面问题有限元分析 等参单元
8.1等参曹单国元华刚度（4节点） 8.2等参单元等效节点力（4节点） 8.3矩形单元（8节点） 8.4等参单元（8节点） 8.5高斯积分法
等参单元刚度（4节点）
4
4
=u ∑= Ni (ξ ,η )ui ,v ∑ Ni (ξ ,η )vi
=i 1 =i 1
4
4
=x ∑= Ni (ξ ,η ) xi , y ∑ Ni (ξ ,η ) yi
i =1
4
y = ∑ Ni (ξ ,η ) yi
i =1

存在的。换句话说，为了使上述等参元能保持较好的精度，整体坐标系下所划分的任意四边形单元必须是
凸四边形，即任意内角都不能大于180°。四边形也不能太歪斜，否则会影响其精度。
利用雅可比的逆矩阵，即可求出整体坐标系下形函数的偏导数：
⎧∂Ni ⎫
⎧∂Ni ⎫
⎪ ⎪ ⎨
∂x
⎪
⎪
⎪ ⎬
=
[J
]−1
⎪ ⎨
∂ξ
⎪ ⎪ ⎬
i=i,j,m,p
为了实现上述结点坐标之间的变换，可利用母元的形函数，得出(ξ,η)和(x,y)之间的坐标变换式。
图形变换具有如下性质: 1. 母元中的坐标线对应于等参元的直线； 2. 四结点正方形母元对应于四个结点可以任意布置的直边四边形等参元； 3. 变换式(2-6-1)能保证相邻等参元的边界位移彼此协调。
《有限元》讲义
2.6 四结点四边形单元
(The four-node quadrilateral element)
前面介绍了四结点的矩形单元 其位移函数:
U = α1 + α 2 x + α3 y + α 4 xy V = α5 + α 6 x + α 7 y + α8 xy
为双线性函数，应力，应变在单元内呈线性变化， 比常应力三角形单元精度高。但它对边界要求严格。本 节介绍的四结点四边形等参元，它不但具有较高的精度，而且其网格划分也不受边界的影响。
对任意四边形单元（图见下面）若仍直接采用前面矩形单元的位移函数，在边界上它便不再是线性 的（因边界不与x,y轴一致），这样会使得相邻两单元在公共边界上的位移可能会出现不连续现象（非协 调元），而使收敛性受到影响。可以验证，利用坐标变换就能解决这个问题，即可以通过坐标变换将整体 坐标中的四边形（图a）变换成在局部坐标系中与四边形方向无关的边长为2的正方形。

其中，
Ni (ai bi x ci y) / 2A。 (i, j, m)
第六章 用有限单元法解平面问题
应变
应用几何方程，求出单元的应变列阵 ：
ε ( u v v u )T x y x y
ui
1 2A
b0i ci
0 ci bi
bj 0 cj
0 cj bj
bm 0 cm
0
vi
cm bm
于单元，称为结点力，以正标向为正。
Fi (Fix Fiy T
－－单元对结点的 作用力，与 Fi 数值 相同,方向相反，作 用于结点。
Fiy vi
Fix i
ui
Fiy
y v j Fjy i
Fix
j
uj
F jx
vm Fmy
um
m Fmx
o
x
第六章 用有限单元法解平面问题
求解方法
（5）将每一单元中的各种外荷载，按虚功 等效原则移置到结点上，化为结点荷 载，表示为
第六章 用有限单元法解平面问题
FEM的概念
§6-2 有限单元法的概念
FEM的概念，可以简述为：采用有限自由度的离 散单元组合体模型去描述实际具有无限自由度的 考察体，是一种在力学模型上进行近似的数值计 算方法，其理论基础是分片插值技术与变分原理。
FEM的分析过程：
1.将连续体变换为离散化结构； 2.单元分析； 3.整体分析。
第六章 用有限单元法解平面问题
FEM
第六章 用有限单元法解平面问题
概述 1.有限元法（Finite Element Method）
简称FEM，是弹性力学的一种近似解法。 首先将连续体变换为离散化结构，然后再利用 分片插值技术与虚功原理或变分方法进行求解。

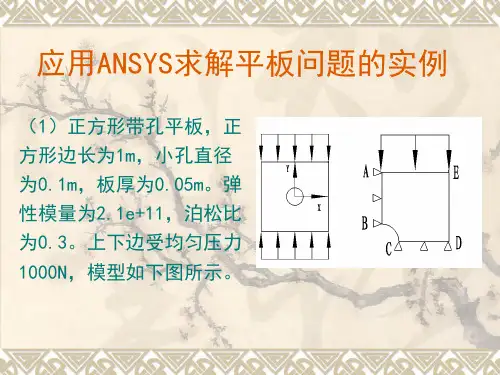
第10章平面和壳问题的有限元分析第1节基本知识严格地说，任何弹性物体都是处在三维受力状态。

因而都是空间问题，但是在一定条件下，许多空间问题可以简化为平面问题，从而使计算工作量大大减少。

典型的平面问题有平面应力问题和平面应变问题。

板壳问题是工程实际中最常遇到的问题之一。

一、平面应力问题平面应力问题是指受力体在z方向上尺寸很小（即呈平板状），外载荷都与z轴垂直，且沿z轴方向没有变化，假设受力体在z方向上的尺寸为h，平分h的平面成为中间平面，简称中面，则在z=±h/2处的外表面上不受任何载荷，如图10-1所示。

在建立模型时，以受力体的中面尺寸建立模型。

图10-1 平面应力问题二、平面应变问题平面应变问题是指受力体在z方向的尺寸很大，所受的载荷又平行于其横截面（垂直于z轴）且不沿长度方向（z方向）变化，即物体的内在因素和外来作用都不沿长度方向变化，如图10-2所示。

对于有些问题，例如挡土墙和水坝的受力问题，虽然其结构不是无限长，而且在靠近两端之处的横截面也往往是变化的，并不符合无限长柱形体的条件，但实践证明，这些问题是很接近于平面应变问题，对于离开两端较远之处，按平面应变问题进行分析计算，得出的结果是可以满足工程实际要求的。

表10-1是常用的平面应力问题和平面应变问题的单元类型和用途。

图10-2 平面应变问题在利用ANSYS进行有限元分析时，将这些单元定义为新的单元后，如平面应力问题，设置单元配置项KEYOPT（3）为Plane stree 或Plane stress with thickness input（考虑板的厚度）；如为平面应变问题，设置单元配置项KEYOPT（3）为Plane strain。

三、壳的问题对于两个曲面所限定的物体，如果曲面之间的距离比物体的其它尺寸小很多，就称之为壳体。

并且这两个曲面称为壳面。

距两壳面等距的点形成的曲面成为中间曲面，简称中面。

对受力体进行有限元分析时，以中面尺寸建立模型。

严格地说，实际的弹性结构都是空间结构，并处于空间受力状 态，属于空间问题，然而，对于某些特定问题，根据其结构和外力 特点可以简化为平面问题来处理。这种近似，可大大减少计算工作 工作量，为有限元分析提供方便。弹性力学平面问题可分为两类：
(1) 平面应变问题： 如图柱形管道和长柱形坝体，具有如下特点：a纵向尺寸远大 于横向尺寸，且各横截面尺寸都相同；b 载荷和约束沿纵向不变， 因此可以认为，沿纵向的位移分量 等于零。
一悬臂梁的力学模型简化和单元划分如图： 在确立了力学模型的基础上，再把原来连续的弹性体离散化， 分为有限个单元，这些单元可以是三结点三角形、四结点任意四边 形、八结点曲边四边形等等。单元之间只在结点处相联结。平面问 题的结点为铰结点。完成单元划分以后，需要对所有单元按次序编 号，就得到了有限元的计算模型。
A
S
U
(
A
*
xx
*
yy
xy
* xy
)
t
dx
dy
上面三个积分的意义为：
W 中的第一个积分表示全部体积力作的虚功；第二个积分表示
自由边界S 上的表面力作的虚功。U 中的积分为
dU
(
x
* x
y
* y
xy
* xy
)
t
dx
dy
它表示单面体四个侧面上的应力在虚应变上作的虚功。
1 力学模型的简化 用有限元法研究实际工程结构的强度与刚度问题，首先要从工 程实际问题中抽象出力学模型，即要对实际问题的边界条件，约束 条件和外载荷进行简化，这种简化应尽可能反映实际情况，使简化 后的弹性力学问题的解答与实际相近，但也不要带来运算上的过分 复杂。 在力学模型简化过程中，必须明确以下几点 ①判断实际结构的问题类型，是 二维问题还是三维 问题；对于 平面问题，是平面应变 问题还是平面应力 问题。 ②结构是否对称 。如果是对称的，要充分利用对称条件，以简 化计算。 ③简化的力学模型必是静定 的或超静定的。

图１２－９ 图１２－８
图１２－１０
(3)设置实常数 对于“Triangle 6node 2”单元，不需要定义实常数 （4）设置材料属性 运行主菜单Main Menu> Preprocessor> Material Props >Material Models（见图１２ －１１），弹出“材料属性” 对话框（见图１２－１２）。 在“材料属性”对话框右侧依 次双击选择Structural > Linear> Elastic> Isotropic，弹 出“弹性模量、泊松比参数设 置”对话框（见图１２－１ ３）。填写数据后，单击 【OK】按扭，完成设置，如 图１２－１４所示。SAVE.
平面问题的有限元案例
——————厚壁圆筒承受压力载 荷
例题：
某厚壁圆筒承受压力载 荷如图1所示，压力 p=10Mpa，圆筒内径 Ri=1400mm圆筒外径 R0=1500mm,材料的弹性 模量E=2.1×105Mpa， 泊松比u=0.3。采用平面 问题的有限元法求解圆 筒沿半径方向的径向应 力和图１２－３０
５.结果分析
（１）位移云图 运行主菜单Main Menu > General Postproc >Read Results >First Set （见图１２－３２），在运行Main Menu > General Postproc >Plot Results >Contour Plot >Nodal Solu（见图１２－３３），弹出 “Contour Nodal Solution Data”对 话框（见图１２－３４）．选择结 点位移，左边框选“DOF solution”， 右边框选“USUM”，即选择总的结 点位移，另选择“Def+undeformed” 复选框．图形窗口出现变形前后的 结构图，并显示位移数值云图（见 图１２－３５）．

第2章 弹性力学平面问题有限单元法2.1 三角形单元(triangular Element)三角形单元是有限元分析中的常见单元形式之一，它的优点是:①对边界形状的适应性较好，②单刚形式及其推导比较简单,故首先介绍之。

一、结点位移和结点力列阵设图为从某一结构中取出的一典型三角形单元。

在平面应力问题中，单元的每个结点上有沿x、y两个方向的力和位移，单元的结点位移列阵规定为： 相应结点力列阵为: (式2-1-1){}⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=m j i m ed d d d m j j i v u v u v u i {}ii j j m X Y X (2-1-1)Y X Y iej m m F F F F ⎧⎫⎪⎪⎪⎪⎧⎫⎪⎪⎪⎪⎪⎪==⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎪⎪⎪⎪⎪⎪⎩⎭二、单元位移函数和形状函数前已述及，有限单元法是一种近似方法，在单元分析中，首先要求假定（构造）一组在单元内有定义的位移函数作为近似计算的基础。

即以结点位移为已知量，假定一个能表示单元内部（包括边界）任意点位移变化规律的函数。

构造位移函数的方法是：以结点(i,j,m)为定点。

以位移(u i ,v i ,…u m v m 3)为定点上的函数值，利用普通的函数插值法构造出一个单元位移函数。

在平面应力问题中，有u,v 两个方向的位移,若假定单元位移函数是线性的,则可表示成:(,)12u u x y x yααα+46y ==+ 5(,)v v x y x ααα+==+ (2-1-2)a式中的6个待定常数α1 ,…, α6 可由已知的6个结点位移分量(3个结点的坐标)确定。

将13个结点坐标(x i,3iy y i ),(x j,y j ),(x m,y m )代入上式得如下两组线性方程: 12i i u x ααα+3=+12j j j x y u αα=+α+3m y (a)12m m u x ααα=++46i y和5i i v x αα=+α+465j j j x y v αα=+α+46m y (b)5m m v x ααα=++利用线性代数中解方程组的克来姆法则,由(a)可解出待定常数1α 、2α 、3α :211A Aα=22A 3A Aα=3Aα=式中行列式:2111i i 1i i i j m j j m m u x y A u x y u x y =j jm mu y A u y u y =3111i i j jm mx u A 2111i i j j m mAx y A x y x y x u x u ===A为△ijm 的面积,只要A不为0,则可由上式解出:112i i j j a u a u ()m m a u A α=++21(2i ij j bu b u )m m b u A α=++ （C）312i i j j c u c u ()m mc u A α=++i j a x y =−j i y x y =−m i j j i y x y 式中:m m j x y a x a x m m i =−y m y y =−m i j y ym i j b y =− b b j i =− （d）3c m i j x x =− j i c m x x =−m j i c x x =−m iy x y =−m为了书写方便，可将上式记为: a xm i j b i jy y =−(,,) i u j m uu u ruuu u r i jc m x x =−(,,)i j m uuu u r uuu u r)m m N x y u N x y u N x y u =++)m x y v 表示按顺序调换下标,即代表采用i,j,m 作轮换的方式便可得到(d)式。