位置关系的相对性

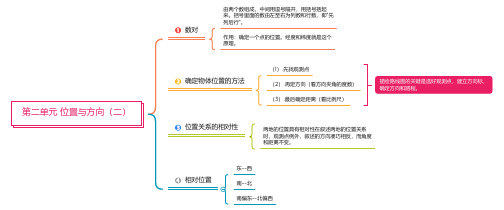
第二单元 位置与方向（二）
数
对 由
两个数组成，中间用逗号隔开，用括号括起
来。

括号里面的数由左至右为列数和行数，即“先
列后行”。

作
用：确定一个点的位置。

经度和纬度就是这个 原理。

确
定物体位置的方法 （1）.先找观测点 （2）.再定方向（看方向夹角的度数） （3）.最后确定距离（看比例尺）
描绘路线图的关键是选好观测点，建立方向标， 确定方向和路程。

位
置关系的相对性 两地的位置具有相对性在叙述两地的位置关系
时，观测点例外，叙述的方向凑巧相反，而角度 和距离不变。

相
对位置 东--西
南--北
南偏东--北偏西。

空间关系知识点总结一、空间概念空间是指周围的环境由物质实体所构成的三维空间。

在这个空间中，物体可以相对移动，相对位置也会发生变化。

在空间中，我们可以观察到物体的位置、形状和大小等属性。

空间关系是指事物在空间中的相对位置关系。

空间关系有三种形式，即相对位置、方位和距离。

1.相对位置：相对位置是指两个物体在空间中的相对位置关系。

当我们描述一个事物所处的位置时，一定要以另一事物为基准来描述，这就是相对位置。

例如，A在B的左边，B在A的右边，这是相对位置的描述。

2.方位：方位是指事物在空间中的朝向关系。

方位由四个基本方向组成，即东、西、南、北。

在地理空间中还有东北、东南、西北、西南等方位。

方位是空间中非常重要的关系，能够帮助我们更准确地描述事物在空间中的位置。

3.距离：距离是指两个事物在空间中的间隔距离。

在空间中，物体可以通过距离来描述物体的相对远近。

距离是空间关系中很重要的一个方面，它可以通过度量直线距离、曲线距离来描述物体之间的相对远近。

二、空间语言描述空间关系可以通过语言来进行描述。

语言描述可以帮助我们更加准确地了解物体在空间中的位置、方位以及距离。

在语言描述中，要注意以下几点：1.使用准确的定位词语：在描述空间关系时，要使用准确的定位词语，如“上、下、左、右、前、后”等。

这些词语可以帮助我们更加准确地描述事物在空间中的位置。

2.使用准确的方向词语：在描述方位时，要使用准确的方向词语，如“东、西、南、北”等。

这些词语可以帮助我们更加准确地描述事物在空间中的朝向关系。

3.使用准确的距离词语：在描述距离时，要使用准确的距离词语，如“远、近、远离、靠近”等。

这些词语可以帮助我们更加准确地描述事物在空间中的相对远近关系。

三、空间关系的认知发展儿童对空间关系的认知发展是一个渐进的过程。

在儿童的认知过程中，从最初的“具体视觉参照”到“图形概念”再到“抽象概念”，儿童对空间关系的认知逐渐升级。

1.具体视觉参照：儿童最开始的认知是基于具体的物体进行的。

六年级下册数学知识点总结 基础数学的知识与运⽤是个⼈与团体⽣活中不可或缺的⼀部分.其基本概念的精炼早在古埃及、美索不达⽶亚及古印度内的古代数学⽂本内便可观见。

下⾯店铺整理了⼀些关于六年级下册数学知识点总结，欢迎⼤家参考! 第⼀单元分数乘法 ⼀、分数乘法 (⼀)分数乘法的意义： 1、分数乘整数与整数乘法的意义相同。

都是求⼏个相同加数的和的简便运算。

例如：65×5表⽰求5个65的和是多少? 1/3×5表⽰求5个1/3的和是多少? 2、⼀个数乘分数的意义是求⼀个数的⼏分之⼏是多少。

例如：1/3×4/7表⽰求1/3的4/7是多少。

4×3/8表⽰求4的3/8是多少. (⼆)、分数乘法的计算法则： 1、分数与整数相乘：分⼦与整数相乘的积做分⼦，分母不变。

(整数和分母约分) 2、分数与分数相乘：⽤分⼦相乘的积做分⼦，分母相乘的积做分母。

注意：当带分数进⾏乘法计算时，要先把带分数化成假分数再进⾏计算。

3、为了计算简便，能约分的要先约分，再计算。

(尽量约分，不会约分的就不约，常考的质因数有11×11=121;13×13=169;17×17=289;19×19=361) 4、⼩数乘分数，可以先把⼩数化为分数，也可以把分数化成⼩数再计算(建议把⼩数化分数再计算)。

(三)、乘法中⽐较⼤⼩的规律 ⼀个数(0除外)乘⼤于1的数，积⼤于这个数。

⼀个数(0除外)乘⼩于1的数(0除外)，积⼩于这个数。

⼀个数(0除外)乘1，积等于这个数。

(四)、分数混合运算的运算顺序和整数的运算顺序相同。

整数乘法的交换律、结合律和分配律，对于分数乘法也同样适⽤。

乘法交换律： a × b = b × a 乘法结合律： ( a × b )×c = a × ( b × c ) 乘法分配律： ( a + b )×c = a c + b c ⼆、分数乘法的解决问题(已知单位“1”的量(⽤乘法)，即求单位“1”的⼏分之⼏是多少) 1、画线段图：(1)两个量的关系：画两条线段图，先画单位⼀的量，注意两条线段的左边要对齐。

知识点一位置关系的相对性1．看图填空。

(1)图书馆在学校()偏()()方向上，距离是()m。

(2)学校在图书馆()偏()()方向上，距离是()m。

(3)学校在少年宫()偏()()方向上，距离是()m。

(4)少年宫在学校()偏()()方向上，距离是()m。

2．选择。

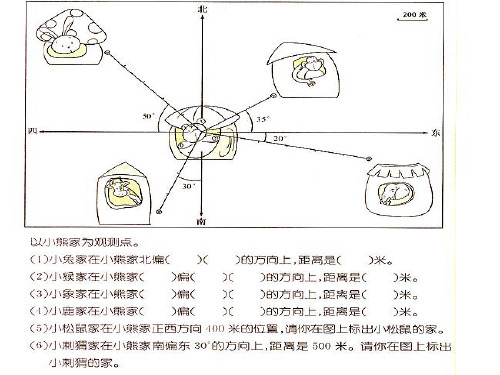
(1)以小猴家为观测点，小松鼠家在()方向。

A．西偏南55°B．南偏西55°C．东偏北55°(2)以小松鼠家为观测点，小猴家在()方向。

A．东偏北35°B．北偏东35°C．南偏西35°知识点二描述并绘制简单的路线图3．一辆汽车从起点站向西偏南35°方向行驶6 km后，又向东偏南30°方向行驶8 km，最后向南行驶4 km到达终点站。

(1)根据上面的描述，把这辆汽车行驶的路线图画完整。

(2)根据路线图，说一说这辆汽车沿原路返回时所行驶的方向和路程。

4．看图回答问题。

(1)根据上面的路线图，填出明明从家去娱乐场和回来时所走的方向和路程。

方向路程时间明明家→体育馆15分钟体育馆→娱乐场7分钟娱乐场→体育馆9分钟体育馆→明明家9分钟全程(2)明明走完全程的平均速度是多少？5．周日，小悦全家开车去“假日旅游度假村”游玩。

从家出发向正西方向行驶10 km，再向西偏南20°方向行驶5 km，最后向南偏东22°方向行驶10 km，就可到达“假日旅游度假村”。

(1)根据上面的描述，画出小悦全家开车去“假日旅游度假村”所行驶的路线图。

(2)根据路线图，说一说小悦全家开车沿原路返回时所行驶的方向和路程。

6．月月家在学校的东偏北45°方向300 m处，东东家在学校的北偏西15°方向300 m 处，如果从月月家去东东家，应向哪个方向走多远才能到达？1．(1)东南45°500(2)西北45°500(3)东北35°350(4)西南35°3502．(1)B(2)A3．(1)略(2)从终点站先向北行驶4 km，再向西偏北30°方向行驶8 km，最后向东偏北35°方向行驶6 km回到起点站。