当前位置：文档之家 › 卷积计算(图解法)

卷积计算(图解法)

  • 格式：ppt
  • 大小：317.50 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

卷积积分及零状态响应的卷积计算法.

卷积积分及零状态响应的卷积计算法.

t
e RC
RCT
T RC t
e RCT 0
RC T RC
(t 0)
u0T T RC
e
t T
t
e RC
ε(t)
➢卷积积分的图解
求f(t)与h(t)的卷积，实质上是求一个新函数
f()h(t)在 由0到t的区间内的定积分。根据定积分的 几何意义，函数在0到t区间内的定积分值，决定于被积 函数f()h(t)的曲线在该区间内与 轴之间所限定的面
§4-6 卷积积分及零状态响 应的卷积计算法
➢ 卷积积分的推导
激励函数的 近似表示
f (t) fa (t) f (0)ε(t) ε(t )
f ( )ε(t ) ε(t 2 )
f (2 )ε(t 2 ) ε(t 3 )
f (n 1) ε(t (n 1) ) ε(t n )
解： [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
1 e t
0
(t 0)
(t 0)
1 1 e t ε(t)
例2 设图示RC串联电路中电压源的电压
t
u(t) u0e T ε(t)
求零状态响应电压uC(t)。
解： 用卷积积分公式求uC(t)，应先求冲激响应
如按
t
r(t) h( ) f (t ) d h(t) f (t)
0
当 0<t <1 时
计算。
r(t ) te ε( )d t e d 1 et
0
0
当 t >1时
r(t ) t e ε( )d t 1
t e d e(t1) et t 1 返回
注意ቤተ መጻሕፍቲ ባይዱ分上、下限

卷积计算(图解法)

卷积计算(图解法)

(1) n<0
x(m) m 0 4 h(n-m) m n-6 n0
y(n) = x(n) ∗ h(n) = 0
x(m) m
(2)在0≤n≤4区间上
0
4 h(n-m) m
n-6 0 n 4
∴ y(n) = ∑ x(m)h(n − m) = ∑1⋅ a
m=0 n m=0
n
n
n−m
=a
n
m=0
∑a
−m
1− a =a −1 1− a
n
−( n+1)
1− a =1− a
1+n
x(m)
(3)在4<n≤6区间上
m 0 4 h(n-m) m n-6 0
1+n
∴ y(n) = ∑x(m)h(n − m)
m=0
4
= ∑1⋅ a
m=0 n
4
n−m
=a
n
m=0
∑a
n−4
4
−m
4 6 n
1− a a −a =a = −1 1− a 1− a
−(1+4)
x(m) m 0 4 h(n-m) m 0 n-6
7
(4)在6<n≤10区间上
∴ y(n) = =
m=n−6
∑x(m)h(n − m)
=a
n m=n−6 −( 4+1)
n
m=n−6
∑1⋅ a
n
n
n−m
∑a
=
4
−m
6
n
10
=a
a
−( n−6)
−a −1 1− a
a
n−4
−a 1− a
综合以上结果， 可归纳如下： 综合以上结果，y(n)可归纳如下： 可归纳如下

04第四章：卷积的计算.ppt

04第四章：卷积的计算.ppt
当t > 0时, ∫ e
0 ∞ 2(t − τ )
u (τ − t )dτ = ∫ e
t
∞
2(t − τ )
1 dτ = 2
2(t − τ )
当t < 0时， e ∫
0
∞
2(t − τ )
u (τ − t )dτ = ∫ e
0
∞
1 2t dτ = e 2
得 所以
∫
∞
e
2(t − τ )
0
1 2t 1 u (τ − t )dτ = e u (−t ) + u (t ) 2 2
4.2卷积的性质 4.2卷积的性质
6.卷积的时移性质 6.卷积的时移性质
若 f 1 (t ) ∗ f 2 (t ) = f (t ) ，则
f1 (t − t1 ) ∗ f 2 (t − t 2 ) = f (t − t1 − t 2 )
利用卷积的时移性可以使时移信号的卷积计算变得大为简单。 利用卷积的时移性可以使时移信号的卷积计算变得大为简单。 4.2例 4.2-5 计算 tu (t ) ∗ u (t − 2) 。 解 由于
f (t ) = f1 (t ) * f 2 (t ) =
∫ f (τ ) f (t − τ )dτ
1 −∞ 2
∞
给定 t 值， f 2 (−τ ) 沿 τ 正轴平移 t ， 的波形， 4.1- （ ； （ 3） 将 得到 f 2 (t − τ ) 的波形， 如图 4.1-2 d） 相乘， （4）将 f1 (τ ) 和 f 2 (t − τ ) 相乘，得到 f1 (τ ) f 2 (t − τ ) ；
f (t ) = tu (t ) ∗ u (t ) =
1 2 t u (t ) ，则 2

电路原理课件-卷积积分

电路原理课件-卷积积分
3
7) t≥7时,
y(t ) 0
注意：积分上下限应由被 积函数存在的时域范围的 上下限确定。
卷积积分在电路分析中的应用
例1、电路如图所示，uS=15e-0.25t(t)V。采用卷积计算uC。
解：以uC为响应，求单位阶跃响应
uC (0 ) uC (0 ) 0
uCf 40 1 0.5V 40 40
t t
t t
t 0
d dt t t
卷积积分上下限分析
t
0
r t h t f t f t h t
卷积符合交换律
δ t f t δ f t dτ τ τ
k 0
f (t ) f a (t )
f ( k ) ( t k ) ( t ( k 1) )
k 0 n 1

k 0 n 1
k 0
n 1
(t k ) (t (k 1) ) f (k )
例2、电路如图，R=10，L=1H，激励uS的波形如图 所示，求零状态响应i(t)。
解：以电流i 为响应，求单位阶跃响应为：
R t 1 g( t ) (1 e L ) ( t ) R 0.1(1 e 10 t ) ( t )
则单位冲激响应为：
dg( t ) h (t ) e 10 t ( t ) dt
40 40 RC 0.05 1s 40 40
uC ( t ) uCf (1 e ) ( t ) 0.5(1 e t ) ( t )V
t
单位阶跃响应为：
g(t ) 0.5(1 e t ) (t )

Z2.14 卷积积分的图解法

Z2.14 卷积积分的图解法

2
Xidian University, ICIE. All Rights Reserved
2.3 卷积积分
第二章 连续系统的时域分析
例1 f (t), h(t) 如图，求yzs(t)= h(t) * f (t) 。 f (-τ ) f ( τt )
解:
h(t)函数形式复杂, 换元为h(τ)； f (t)换元为 f (τ)
2
② 0≤t ≤1时 ③ 1≤t ≤2 时
yzs (t)
t 1 d 1 t2
02
4
yzs (t)
t 1 d 1 t 1
t1 2
24
0 t t-11 tt-1 2 3 t yf (t )
④ 2≤t ≤3时
yzs (t)
2 1 d 1 t2 1 t 3
t1 2
4 24
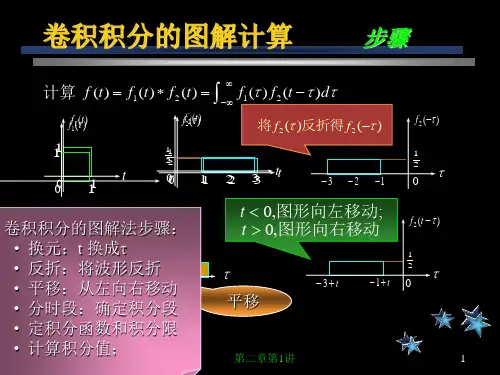
f (τ)反折→ f (-τ)平移t f(t -τ) ① t < 0时 , f (t -τ→)向左移
f ( t -τ) h(τ) = 0，故 yzs(t) = 0 t>0 时, f (t -τ)向右移
f (t -τ ) t-1 t
01
τt
1 h ( tτ ) 2
பைடு நூலகம்
0
2
t-1 t t-1 t 2
τt
h(τ )f (t -τ ) 1
例2 f1(t), f2(t)如图，已知 y(t) = f1(t)* f2(t)，求y(6) =？
解：
y(6)
f1( )
f2 (6
) d
4
Xidian University, ICIE. All Rights Reserved
2.3 卷积积分
y(6)

计算卷积的方法.ppt

计算卷积的方法.ppt
' t
dg ( t ) r ( t ) e ( t ) h ( t ) e ( t ) dt
de (t) *g(t) dt
e ( t ) e ( t ) u ( t )
de ( t ) d ( e ( t ) u ( t ))de ( t ) u ( t ) e ( t ) ( t ) dt dt dt
方法一:

h (t )
t
e( )
0


*
0
h(t ) 非零值下限是－ 卷积分下限是零 u( ) 非零值下限是 0
h(t ) 非零值上限是 t 卷积分上限是 t u( ) 非零值上限是
若两个函数的左边界分别为tl1,tl2,右边界分别为 tr1,tr2,积分的 下限为max[tl1,tl2];积分的上限为min[tr1,tr2].


f f ( ) f ( t ) d 1 2 1 2 f
0 t-2 1
t
3 . if 1 t 2
1
b ab 2 ab 2 t a ( t ) d ( t ) 0 t 0 2 4 4
t
a t-2 0 t 1
ab (2 t 1 ) 4
2.各分段内卷积积分限的确定 。
分解成单位阶跃分量之和
f (t1 )
f( t t ) 1 1 f ( 0)
t1
t1
u ( t ) g ( t ) DaHarma ln tegr
*.Duharmal integral
r(t) e(0 )g(t) e ( )g(t )d 0
1
b ab 2 1 f f a ( t ) d ( t ) 1 2 0 02 4

第二章第3讲 卷积

第二章第3讲 卷积



[ f () * f ()]d f (t) * f ()d f (t) * f ()d
1 2 1 2 2 1
t
t
t
证明：

[ f ( ) * f
1 t 1
t
2
( )]d [ f1 ( ) f 2 ( )d ]d
[ f1 (t )u(t t1 )] [ f 2 (t )u(t t2 )]
信号与系统 同济大学汽车学院 魏学哲 weixzh@
g (t ) f1 ( )u( t1 ) f 2 (t )u(t t2 )d


结合律应用于系统分析,相当于串联系统的冲激响 应,等于串联的各子系统冲激响应的卷积
信号与系统 同济大学汽车学院 魏学哲 weixzh@
卷积的微分与积分
df2 (t ) df1 (t ) d [ f1 (t ) * f 2 (t )] f1 (t ) * f 2 (t ) * dt dt dt

t t2
t1
f1 ( ) f 2 (t )d
t1 t t2
t
积分限是： 例：
f1(t ) 2e u(t )
g (t )

f 2 (t ) u(t ) u(t 2)
求
f1 ( ) f 2 (t )d
信号与系统 同济大学汽车学院 魏学哲 weixzh@
f1( ) 1 f2(1-) 2
f1( ) 1 f2(2-) 2
f1( )
f2(3-)
2
c
c
c
c
-1
0

f1() f2(-)

信号与系统-卷积积分

信号与系统-卷积积分
信号与系统
§2.6 卷积
信号与系统
§2.6.1 卷积定义
定义： 设有两个 函数 f1(t) f2 (t) ，积分
f (t) f1( ) f2(t )d
称为 f1(t) f2 (t) 的卷积积分，简称卷积，记为 f (t) f1(t) f2(t) 或 f (t) f1(t) f2(t)
t 0 , f2 ( ) 未移动 t 0 , f2 ( ) 右移 f2 (t ) t 0 , f2 ( ) 左移 f2 (t )
3
f2(t )
2
1 O 1 t3
t
下限
上限
f2(t )
t-3
t
f1( ) f2 (t ) -1
1
当
t
从
到
变化时，3对应的 2
f2(t )
从左向右移动。
f (t) f1( ) f2 (t )d
对τ延时t，
－(τ- t)= t- τ
积分结果为t 的函数
1.
积分变量改为
2.
f2(t)
f2 ( ) 反折
时延
f2( )
f2(t
)
3.相乘 f1( ) f2 (t )
4.乘积的积分 f1( ). f2 (t )d
信号与系统
§2.6.3 卷积图解过程
例 ：f1 (t )
f1
(Gt )2
(t
),
f2 (t )
t [u(t) 2
u(t
3)]
f1( )
1
1 O 1 t
f2(t )
3 2
t
t
1
1 O
f
1(
2
)
3
2
O

卷积

卷积

1 1 2
1 (t ) d 2
t2 t 1 4 4 16
h(t ) 1
1 2
(c ) 1 t
3 2
1
0
t 1
3 2

(c ) 1 t
1 e(t ) * h(t ) 1 1 (t )d 2 2 3 3 t 4 16
X
第 12 页
第 14 页
X
。
• 练习
已知
1 f1 ( t ) 0 t 1 t 1 t f 2 (t ) 2 ( 0 t 3)
第 15 页
求卷积。
解：
t t 1 4 2 4 t g( t ) 2 t t 2 4 2 0
2
g (t )
1 2
1
0(a) t Nhomakorabeat
1 (a) t 2
1
e(t ) * h(t ) 0
X
第 11 页
h(t )
1 2
e( )
1
1 (b) t 1 2

e(t ) * h(t )
1t (b) t 1 2
e( )
0
1

t

§2.６卷积
•卷积
•利用卷积积分求系统的零状态响应
•卷积图解说明
•卷积积分的几点认识
第
一．卷积（Convolution）
设有两个 函数
2 页
f1 (t ) f 2 (t ) ，积分
f (t ) f1 ( ) f 2 (t ) d


称为
f1 (t ) f 2 (t ) 的卷积积分，简称卷积，记为

第二章卷积图解计算

第二章卷积图解计算
卷积积分的图解计算
计算 f (t) = f1(t) ∗ f2 (t) = ∫−∞ f1(τ ) f2 (t −τ )dτ
( ff1τt)) 1(
() ff22(τt)
1 1 2 2
步骤
∞
将f2 (τ )反 得f2 (− ) 折 τ
f2 (−τ)
1 2
1 1
0 0
1 1
t
f1(τ )
0 τ 0
1 1
2 2
1Байду номын сангаас
0
1 +t −3
−1+ t
τ
−1+ t
f2 (t −τ )
1 2
0
τ
平移
第二章第1讲
1
例
1
计算 f (t) = f1(t) ∗ f2 (t) = ∫−∞ f1(τ ) f2 (t −τ )dτ
当 −1+ t < 0 即 t < 1 时： f 2 (t −τ ) 和 f1 (τ ) 没有公共的重叠部分， 1 2 故卷积 f (t) = f1 (t) ∗ f2 (t) = 0 t 0 1 2 3
1 1 1× dτ = (4 − t) −3+t 2 2
1
即为重叠部分的面积。 当 −3+t ≥1 即 t ≥ 4 时： f 2 (t −τ ) 和 f1 (τ ) 没有公共的重叠部分， 故卷积 f (t) = f1 (t) ∗ f2 (t) = 0
第二章第1讲 3
f 2 (t −τ ) f1(τ)
4
f (t)
∞
f 2 (t −τ ) f1(τ)
1
−3 + t −1+ t 0
1

卷积图解法

卷积图解法
b
* 0 -1 1 1 b f1 a[u(t ) u(t 1)]t t f 2 (t 1)[u (t 1) u (t 1)] j 2 2 2 f 2 f1 f 2 ( ) f1 (t ) du (t ti t j )
i 1 j 1 ti
p q i 1 i
j 1

i 1 j 1
f (t )h (t )[u( t )u(t t
j i
j
)]d
由以上讨论可知:
得出卷积积分的上下限和定义域如下:
f h

i 1 j 1
p
q
t t j
f i ( ) h j (t ) du (t t i t j )


u ( 1)u (t 2)d u ( 1)u (t 3)d
t 2


d d (t 2 1) (t 3 1) 1
1
t 2
t 3
1

du (t 2 1) du (t 3 1)
e ( ) g (t )d
'
t
0

预习§2.7 作业 p85 2-19
(a),(b),(f)
1 1
t 3
(t 3)u (t 3) (t 4)u (t 4)
*. *.快速定限表 若参与卷积的两个函数fs(t)和fl(t)都是只有一个定义段,它 们的时限长度分别为TS和TL,并且TS< TL,长函数fl(t)的左 右时限分别为LL和RL,而短函数fs(t)的的左右时限分别为LS 和RS,并规定积分号内括号统一只表示 f s ( ) f l (t ) 即只反 转时限长的函数. rs

计算卷积的方法

计算卷积的方法

.某复合系统如图所示 ,两个子系统的冲激响应 分别为 h1 (t ) u (t ), h2 (t ) u (t 1) u (t 2) 1. 求该系统的冲激响应 h(t). 2. 当系统的输入 f(t) ' (t )时,求该复合系统的零状态 响应y zs (t ).

f(t)
tj0tj1f1f21快速定限表若参与卷积的两个函数fst和flt都是只有一个定义段它们的时限长度分别为ts和tl并且tstl长函数flt的左右时限分别为ll和rl而短函数fst的的左右时限分别为lsrs并规定积分号内括号统一只表示即只反转时限长的函数
*计算卷积的方法
1.用图解法计算卷积
分段时限
2.用函数式计算卷积 3.利用性质计算卷积
b
* 0 -1 1 1 b f 2 (t 1)[ u (t 1) u (t 1)] f1 a[u(t ) u(t 1)] t t j 2 2 2 f 2 f1 f 2 ( ) f1 (t ) du (t ti t j )
i 1 j 1 ti
t
b
0
f2(t)
解:1. t 0
0
2
t-2 0 1 t a t-2 0 1
重合面积为零:f1(t)*f2(t)=0
2.if 0 t 1


f1 f 2 f1 ( ) f 2 (t )d
0 t-2 1
t
3.if 1 t 2
1
b ab a (t )d (t ) 2 0 2 4
e(t )
h2 (t )
h1 (t )
h3 (t )

r (t )

信号与系统计算卷积积分的图示解析法

信号与系统计算卷积积分的图示解析法

h( t )
y( t ) t 3
t 1 2 t 1 2
t 1 2
y( t ) 2
t 1 2
y( t ) 3 t
t 1 2
t 1 2 t 1 2
y( t ) [u( t 2) u( t 2)] [u( t 1) u( t 1)]
y( t )
0
BC 2BC ( t )d (t 1) 3 3
t30 t3 2
x ( )
h( t )
t3
2
t
BC BC 2 y( t ) ( t )d ( t +4t +5) (3 t 5) 3 6 t 3
x ( )
假定参与卷积的两个函数都只有一个定 义段，即：
fl ( t ) ()u( t Ll ) u( t Rl )
f s ( t ) ()u( t Ls ) u( t Rs )
其中，l、s分别表示长短，L、R分别表 示左右，则时限长度分别为：
Tl Rl Ll，Ts Rs Ls
h( )
t0
x ( )
t3
t
y( t ) 0
(t 0)
h( t )
x ( )
t0 t2
t3
t
y( t )
0
t
BC BC 2 ( t )d t 3 6
(0 t 2)
h( t )
x ( )
t2 t30
t3
2
t
(2 t 3)
y( t )
例
x ( t ) C [u( t ) u( t 2)],
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a
n4
a 1 a
综合以上结果，y(n)可归纳如下：
0, 1 n 1 a , 1 a n 4 1 n a a y ( n) , 1 a a n4 a 7 , 1 a 0 ,
n0 0n4 4n6 6 n 10 10 n
x( m )
(4)在6<n≤10区间上
m n 6
m 0 4 h(n-m) m
m
y ( n)
x ( m) h( n m)
a
n m n 6 ( 4 1)
n
m n 6
1 a
n
n
nm
a

4
0 n-6
7
6
n
10
a
a
( n 6)
a 1 1 a
解 参看图，分段考虑如下：
h(m)
x(m)
n
n
0
0
6 h(n-m)
m
4
n-6
(1)对于n<0； (2)对于0≤n≤4； (3)对于n>4，且n-6≤0，即4<n≤6； (4)对于n>6，且n-6≤4，即6<n≤10； (5)对于(n-6)>4，即n>10。
n
(1) n<0
x(m) m
0
y ( n) x ( n) h( n) 0
卷积计算——图解法
y ( n)
m
x(m)h(n m) x(n) h(n)

计算步骤如下：
(1) 翻褶：先在坐标轴 m 上画出 x(m) 和 h(m) ， 将h(m)以纵坐标为对称轴折叠成 h(-m)。
(2) 移位：将 h(-m) 移位 n ，得 h(n-m) 。当 n 为 正数时，右移n；当n为负数时，左移n。 (3)相乘：将h(n-m)和x(m)的对应序列值相乘。
(4)相加：把所有的乘积累加起来，即得y(n)。
计算卷积时，一般要分几个区间分别加以 考虑，下面举例说明。 例 已知x(n)和h(n)分别为：
1, 0 n 4 x ( n) 其它 0,
和
a n , 0 n 6 h( n) 其它 0,
a为常数，且1<a，试求x(n)和h(n)的卷积。
4
h(n-m) m
n-6
n0
x(m) m 0 4 h(n-m) m n-6 0 n 4
(2)在0≤n≤4区间上
y ( n) x ( m) h( n m) 1 a
m 0 n m 0
n
n
nm
a
n
m 0
a
m
1 a a 1 a 1
nห้องสมุดไป่ตู้
( n 1)
1 a 1 a
1 n
x(m)
(3)在4<n≤6区间上
4
m 0 4 h(n-m)
y ( n) x ( m) h ( n m)
m 0
1 a
m 0 n
4
nm
a
n
m 0 (1 4 )
a
n4
4
m
m
n-6 0
1 n
4 6 n
1 a a a a 1 1 a 1 a