当前位置：文档之家 › 卷积计算(图解法)

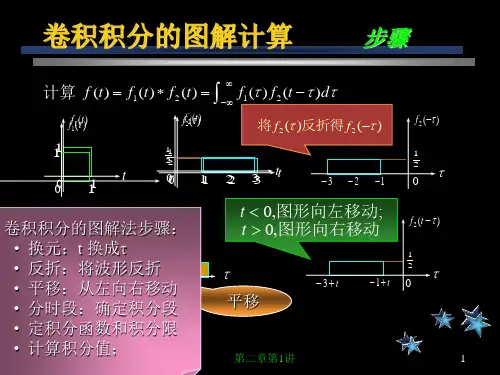
卷积计算(图解法)

  • 格式：ppt
  • 大小：323.00 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

04第四章：卷积的计算.ppt

04第四章：卷积的计算.ppt
当t > 0时, ∫ e
0 ∞ 2(t − τ )
u (τ − t )dτ = ∫ e
t
∞
2(t − τ )
1 dτ = 2
2(t − τ )
当t < 0时， e ∫
0
∞
2(t − τ )
u (τ − t )dτ = ∫ e
0
∞
1 2t dτ = e 2
得 所以
∫
∞
e
2(t − τ )
0
1 2t 1 u (τ − t )dτ = e u (−t ) + u (t ) 2 2
4.2卷积的性质 4.2卷积的性质
6.卷积的时移性质 6.卷积的时移性质
若 f 1 (t ) ∗ f 2 (t ) = f (t ) ，则
f1 (t − t1 ) ∗ f 2 (t − t 2 ) = f (t − t1 − t 2 )
利用卷积的时移性可以使时移信号的卷积计算变得大为简单。 利用卷积的时移性可以使时移信号的卷积计算变得大为简单。 4.2例 4.2-5 计算 tu (t ) ∗ u (t − 2) 。 解 由于
f (t ) = f1 (t ) * f 2 (t ) =
∫ f (τ ) f (t − τ )dτ
1 −∞ 2
∞
给定 t 值， f 2 (−τ ) 沿 τ 正轴平移 t ， 的波形， 4.1- （ ； （ 3） 将 得到 f 2 (t − τ ) 的波形， 如图 4.1-2 d） 相乘， （4）将 f1 (τ ) 和 f 2 (t − τ ) 相乘，得到 f1 (τ ) f 2 (t − τ ) ；
f (t ) = tu (t ) ∗ u (t ) =
1 2 t u (t ) ，则 2

电路原理课件-卷积积分

电路原理课件-卷积积分
3
7) t≥7时,
y(t ) 0
注意：积分上下限应由被 积函数存在的时域范围的 上下限确定。
卷积积分在电路分析中的应用
例1、电路如图所示，uS=15e-0.25t(t)V。采用卷积计算uC。
解：以uC为响应，求单位阶跃响应
uC (0 ) uC (0 ) 0
uCf 40 1 0.5V 40 40
t t
t t
t 0
d dt t t
卷积积分上下限分析
t
0
r t h t f t f t h t
卷积符合交换律
δ t f t δ f t dτ τ τ
k 0
f (t ) f a (t )
f ( k ) ( t k ) ( t ( k 1) )
k 0 n 1

k 0 n 1
k 0
n 1
(t k ) (t (k 1) ) f (k )
例2、电路如图，R=10，L=1H，激励uS的波形如图 所示，求零状态响应i(t)。
解：以电流i 为响应，求单位阶跃响应为：
R t 1 g( t ) (1 e L ) ( t ) R 0.1(1 e 10 t ) ( t )
则单位冲激响应为：
dg( t ) h (t ) e 10 t ( t ) dt
40 40 RC 0.05 1s 40 40
uC ( t ) uCf (1 e ) ( t ) 0.5(1 e t ) ( t )V
t
单位阶跃响应为：
g(t ) 0.5(1 e t ) (t )

常用卷积公式(二)

常用卷积公式(二)

常用卷积公式(二)常用卷积公式1. 一维离散卷积公式：卷积是信号处理中一种常见的运算方法，用于将两个信号合并成一个新的信号。

一维离散卷积公式如下：y[n] = x[n] * h[n] = ∑(k=-∞到∞) x[k] * h[n-k]其中，x[n]表示输入信号，h[n]表示卷积核，y[n]表示输出信号，∑表示求和运算。

例子：假设有两个一维信号x[n] = {1, 2, 3, 4, 5}和h[n] = {1, 1, 1}, 根据卷积公式计算得到输出信号y[n]如下：y[0] = 1*1 = 1y[1] = 1*2 + 1*1 = 3y[2] = 1*3 + 1*2 + 1*1 = 6y[3] = 1*4 + 1*3 + 1*2 + 1*1 = 10y[4] = 1*5 + 1*4 + 1*3 + 1*2 = 14所以，输出信号y[n] = {1, 3, 6, 10, 14}。

2. 二维离散卷积公式：在图像处理领域，经常使用二维卷积来处理图像。

二维离散卷积公式如下：Y[i, j] = ∑(m=-∞到∞)∑(n=-∞到∞) X[i-m, j-n] * H[m, n]其中，X[i, j]表示输入图像的像素，H[m, n]表示卷积核的值，Y[i, j]表示输出图像的像素，∑表示求和运算。

例子：假设有一个3x3的输入图像X和一个2x2的卷积核H，如下：X = | 1 2 3 || 4 5 6 || 7 8 9 |H = | 1 1 || 1 1 |根据卷积公式计算得到输出图像Y如下：Y[0, 0] = 1*1 + 2*1 + 4*1 + 5*1 = 12Y[0, 1] = 1*2 + 2*1 + 3*1 + 4*1 = 12Y[0, 2] = 2*2 + 3*1 + 5*1 + 6*1 = 21Y[1, 0] = 4*1 + 5*1 + 7*1 + 8*1 = 27Y[1, 1] = 4*2 + 5*2 + 6*1 + 7*1 + 8*1 + 9*1 = 45Y[1, 2] = 5*2 + 6*2 + 8*1 + 9*1 = 46Y[2, 0] = 7*1 + 8*1 + 7*1 + 8*1 = 30Y[2, 1] = 7*2 + 8*2 + 9*1 + 7*1 + 8*1 + 9*1 = 57Y[2, 2] = 8*2 + 9*2 + 8*1 + 9*1 = 59所以，输出图像Y为：Y = | 12 12 21 || 27 45 46 || 30 57 59 |3. 一维连续卷积公式：一维连续卷积公式可以用于信号的模拟处理。

卷积计算(图解法)

卷积计算(图解法)
Байду номын сангаас
an4 a7
1 a
,
6 n 10
2021/3/11
0,
10 n 8
(4)相加：把所有的乘积累加起来，即得y(n)。
2021/3/11
1
计算卷积时，一般要分几个区间分别加以 考虑，下面举例说明。
例 已知x(n)和h(n)分别为：
1, 0 n 4 x(n) 0, 其它
an , 0 n 6
和 h(n)
0,
其它
a为常数，且1<a，试求x(n)和h(n)的卷积。
2021/3/11
5
x(m)
(3)在4<n≤6区间上
4
y(n) x(m)h(n m)
m0
m 04
h(n-m)
4
4
1 anm an am
m0
m0
m
n-6 0
46 n
an 1 a(14) an4 a1n
1 a1
1 a
2021/3/11
6
x(m)
(4)在6<n≤10区间上
n
y(n) x(m)h(n m)
2021/3/11
2
解 参看图，分段考虑如下：
x(m)
n 04
h(m)
n 06
h(n-m)
(1)对于n<0；
n-6 n
(2)对于0≤n≤4；
(3)对于n>4，且n-6≤0，即4<n≤6；
(4)对于n>6，且n-6≤4，即6<n≤10；
(5)对于(n-6)>4，即n>10。
2021/3/11
m
3
(1) n<0

计算卷积的方法.ppt

计算卷积的方法.ppt
' t
dg ( t ) r ( t ) e ( t ) h ( t ) e ( t ) dt
de (t) *g(t) dt
e ( t ) e ( t ) u ( t )
de ( t ) d ( e ( t ) u ( t ))de ( t ) u ( t ) e ( t ) ( t ) dt dt dt
方法一:

h (t )
t
e( )
0


*
0
h(t ) 非零值下限是－ 卷积分下限是零 u( ) 非零值下限是 0
h(t ) 非零值上限是 t 卷积分上限是 t u( ) 非零值上限是
若两个函数的左边界分别为tl1,tl2,右边界分别为 tr1,tr2,积分的 下限为max[tl1,tl2];积分的上限为min[tr1,tr2].


f f ( ) f ( t ) d 1 2 1 2 f
0 t-2 1
t
3 . if 1 t 2
1
b ab 2 ab 2 t a ( t ) d ( t ) 0 t 0 2 4 4
t
a t-2 0 t 1
ab (2 t 1 ) 4
2.各分段内卷积积分限的确定 。
分解成单位阶跃分量之和
f (t1 )
f( t t ) 1 1 f ( 0)
t1
t1
u ( t ) g ( t ) DaHarma ln tegr
*.Duharmal integral
r(t) e(0 )g(t) e ( )g(t )d 0
1
b ab 2 1 f f a ( t ) d ( t ) 1 2 0 02 4

Z2.14 卷积积分的图解法

Z2.14 卷积积分的图解法
2.3 卷积积分
知识点Z2.14
第二章 连续系统的时域分析
卷积积分的图解法ห้องสมุดไป่ตู้
主要内容：
1. 图解法步骤 2. 图解法作用
基本要求：
1. 掌握图解法 2. 会用图解法求某一点的卷积结果
1
Xidian University, ICIE. All Rights Reserved
2.3 卷积积分 Z2.14 卷积积分的图解法
f (τ)反折→ f (-τ)平移t f(t -τ) ① t < 0时 , f (t -τ→)向左移
f ( t -τ) h(τ) = 0，故 yzs(t) = 0 t>0 时, f (t -τ)向右移
f (t -τ ) t-1 t
01
τt
1 h ( tτ ) 2
0
2
t-1 t t-1 t 2
τt
h(τ )f (t -τ ) 1
2
② 0≤t ≤1时 ③ 1≤t ≤2 时
yzs (t)
t 1 d 1 t2
02
4
yzs (t)
t 1 d 1 t 1
t1 2
24
0 t t-11 tt-1 2 3 t yf (t )
④ 2≤t ≤3时
yzs (t)
2 1 d 1 t2 1 t 3
t1 2
4 24
第二章 连续系统的时域分析
f1(t) * f2 (t)
f1 (
)
f2
(t
)d
卷积过程可分解为四步：
(1)换元： t 换为τ→得 f1(τ)， f2(τ) (2)反转平移：由 f2(τ)反转→ f2(–τ)右移t → f2(t-τ) (3)乘积： f1(τ) f2(t-τ) (4)积分： τ从 –∞到∞对乘积项积分。 注意：t为参变量。

第二章卷积图解计算

第二章卷积图解计算
卷积积分的图解计算
计算 f (t) = f1(t) ∗ f2 (t) = ∫−∞ f1(τ ) f2 (t −τ )dτ
( ff1τt)) 1(
() ff22(τt)
1 1 2 2
步骤
∞
将f2 (τ )反 得f2 (− ) 折 τ
f2 (−τ)
1 2
1 1
0 0
1 1
t
f1(τ )
0 τ 0
1 1
2 2
1Байду номын сангаас
0
1 +t −3
−1+ t
τ
−1+ t
f2 (t −τ )
1 2
0
τ
平移
第二章第1讲
1
例
1
计算 f (t) = f1(t) ∗ f2 (t) = ∫−∞ f1(τ ) f2 (t −τ )dτ
当 −1+ t < 0 即 t < 1 时： f 2 (t −τ ) 和 f1 (τ ) 没有公共的重叠部分， 1 2 故卷积 f (t) = f1 (t) ∗ f2 (t) = 0 t 0 1 2 3
1 1 1× dτ = (4 − t) −3+t 2 2
1
即为重叠部分的面积。 当 −3+t ≥1 即 t ≥ 4 时： f 2 (t −τ ) 和 f1 (τ ) 没有公共的重叠部分， 故卷积 f (t) = f1 (t) ∗ f2 (t) = 0
第二章第1讲 3
f 2 (t −τ ) f1(τ)
4
f (t)
∞
f 2 (t −τ ) f1(τ)
1
−3 + t −1+ t 0
1

卷积图解法

卷积图解法
t ll
rs
0
.d
.d
ls
ls
t rl
.d
0 t
定义域和卷积结果
例: 1.求出关于 的不定积分
2
f(t)
h(t)
1
4 5 1 3

f s ( )hl (t )d 2 1d 2
2.将两函数的时限值两两相加,得出定义域 1+4=5; 1+5=6; 3+4=7; 3+5=8 3.确定积分限


u ( 1)u (t 2)d u ( 1)u (t 3)d
t 2


d d (t 2 1) (t 3 1) 1
1
t 2
t 3
1

du (t 2 1) du (t 3 1)
0.25ab
0 1 2 3
结语:若f1(t)与f2(t)为有限宽度的脉冲,f1*f2的面积为f1和 f2面 积之积, f1*f2的宽度为f1和 f2宽度之和. Gtk [(t t j ) t i ] 方法二.利用门函数直接计算卷积分
Gtk [(t t j ) t i ] u ( t i )u (t t j )
4...if ...2 t 3
b f1 f 2 a (t )d t 2 2 ab ab 2 1 (t ) 1t 2 (3 2t t 2 ) 4 4
1
ab (2t 1) 4
t-2
0
1 t
0 t-2 1
t
5...if ...3 t .......... f1 f 2 0

卷积优秀课件

卷积优秀课件
t2 2 1 t2 1 t 3
4 24
8
r(t) e(t) h(t) e( )h(t )d
e( )
h(t )
t
(4) 3 t 3 2
e(t) h(t) 1 t 2 1 t 3 4 24
(5) 3 t e(t) h(t) 0
9
r(t) e(t) h(t) e( )h(t )d
[
f1
(t
)
f2 (t)]
f1
(t
)
d dt
f2 (t)
Hale Waihona Puke d dtf1(t)
f2 (t)
t
t
[ f1() f2 ()]d f1(t) f2 ()d
t
f2 (t) f1()d
14
卷积旳微分和积分性质旳推论
f (t) f1(t) f2 (t)
f (i) (t)
f1( j) (t)
y(t) y(t) (t) y(t t0 ) y(t) (t t0 ) f1(t) f2 (t) (t t0 )
f1(t) f2 (t t0 ) f1(t t0 ) f2 (t)
20
P84 2 14(1) f (t) u(t) u(t 1),求s1(t) f (t) f (t)
f1 f2 t d
3
1
2
r(t) e(t) h(t) e( )h(t )d
e(t)或e( )
h(t)或h( )
1
2
t或
t或
h( )
h(t )
1 t
2
t
4
r(t) e(t) h(t) e( )h(t )d
e(t)或e( )
(1) t 1 2

计算卷积的方法

计算卷积的方法

.某复合系统如图所示 ,两个子系统的冲激响应 分别为 h1 (t ) u (t ), h2 (t ) u (t 1) u (t 2) 1. 求该系统的冲激响应 h(t). 2. 当系统的输入 f(t) ' (t )时,求该复合系统的零状态 响应y zs (t ).

f(t)
tj0tj1f1f21快速定限表若参与卷积的两个函数fst和flt都是只有一个定义段它们的时限长度分别为ts和tl并且tstl长函数flt的左右时限分别为ll和rl而短函数fst的的左右时限分别为lsrs并规定积分号内括号统一只表示即只反转时限长的函数
*计算卷积的方法
1.用图解法计算卷积
分段时限
2.用函数式计算卷积 3.利用性质计算卷积
b
* 0 -1 1 1 b f 2 (t 1)[ u (t 1) u (t 1)] f1 a[u(t ) u(t 1)] t t j 2 2 2 f 2 f1 f 2 ( ) f1 (t ) du (t ti t j )
i 1 j 1 ti
t
b
0
f2(t)
解:1. t 0
0
2
t-2 0 1 t a t-2 0 1
重合面积为零:f1(t)*f2(t)=0
2.if 0 t 1


f1 f 2 f1 ( ) f 2 (t )d
0 t-2 1
t
3.if 1 t 2
1
b ab a (t )d (t ) 2 0 2 4
e(t )
h2 (t )
h1 (t )
h3 (t )

r (t )

信号与系统计算卷积积分的图示解析法

信号与系统计算卷积积分的图示解析法

h( t )
y( t ) t 3
t 1 2 t 1 2
t 1 2
y( t ) 2
t 1 2
y( t ) 3 t
t 1 2
t 1 2 t 1 2
y( t ) [u( t 2) u( t 2)] [u( t 1) u( t 1)]
y( t )
0
BC 2BC ( t )d (t 1) 3 3
t30 t3 2
x ( )
h( t )
t3
2
t
BC BC 2 y( t ) ( t )d ( t +4t +5) (3 t 5) 3 6 t 3
x ( )
假定参与卷积的两个函数都只有一个定 义段，即：
fl ( t ) ()u( t Ll ) u( t Rl )
f s ( t ) ()u( t Ls ) u( t Rs )
其中，l、s分别表示长短，L、R分别表 示左右，则时限长度分别为：
Tl Rl Ll，Ts Rs Ls
h( )
t0
x ( )
t3
t
y( t ) 0
(t 0)
h( t )
x ( )
t0 t2
t3
t
y( t )
0
t
BC BC 2 ( t )d t 3 6
(0 t 2)
h( t )
x ( )
t2 t30
t3
2
t
(2 t 3)
y( t )
例
x ( t ) C [u( t ) u( t 2)],
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(1) n<0
x(m) m 0 4 h(n-m) m n-6 n0
y(n) = x(n) ∗ h(n) = 0
x(m) m
(2)在0≤n≤4区间上
0
4 h(n-m) m
n-6 0 n 4
∴ y(n) = ∑ x(m)h(n − m) = ∑1⋅ a
m=0 n m=0
n
n
n−m
=a
n
m=0
∑a
−m
1− a =a −1 1− a
n
−( n+1)
1− a =1− a
1+n
x(m)
(3)在4<n≤6区间上
m 0 4 h(n-m) m n-6 0
1+n
∴ y(n) = ∑x(m)h(n − m)
m=0
4
= ∑1⋅ a
m=0 n
4
n−m
=a
n
m=0
∑a
n−4
4
−m
4 6 n
1− a a −a =a = −1 1− a 1− a
−(1+4)
x(m) m 0 4 h(n-m) m 0 n-6
7
(4)在6<n≤10区间上
∴ y(n) = =
m=n−6
∑x(m)h(n − m)
=a
n m=n−6 −( 4+1)
n
m=n−6
∑1⋅ a
n
n
n−m
∑a
=
4
−m
6
n
10
=a
a
−( n−6)
−a −1 1− a
a
n−4
−a 1− a
综合以上结果， 可归纳如下： 综合以上结果，y(n)可归纳如下： 可归纳如下
0, 1+n 1− a , 1− a n−4 1+n a − a y(n) = , 1− a an−4 − a7 , 1− a 0,
n<0 0≤n≤4 4<n≤6 6 < n ≤ 10 10 < n
计算卷积时， 计算卷积时，一般要分几个区间分别加以 考虑，下面举例说明。 考虑，下面举例说明。 已知x(n)和h(n)分别为： 分别为： 例 已知 和 分别为
1, 0 ≤ n ≤ 4 x(n) = 其它 0,
和
an , 0 ≤ n ≤ 6 h(n) = 其它 0,
a为常数，且1<a，试求 为常数， 的卷积。 为常数 ，试求x(n)和h(n)的卷积。 和 的卷积
参看图 分段考虑如下： 解 参看图，分段考虑如下：
h(m) x(m) n n 0 4 n-6 0 6 h(n-m) m n
(1)对于 对于n<0； 对于 ； (2)对于 对于0≤n≤4； 对于 ； (3)对于 对于n>4，且n-6≤0，即4<n≤6； 对于 ， ， ； (4)对于 对于n>6，且n-6≤4，即6<n≤10； ， ， ； 对于 (5)对于 对于(n-6)>4，即n>10。 对于 ， 。
卷积计算——图解法
y(n) =
m=−∞
∑x(m)h(n − m) = x(n) ∗ h(n)
∞
计算步骤如下： 计算步骤如下： (1) 翻褶 ： 先在坐标轴 m 上画出 x(m) 和 h(m) ， 翻褶： 先在坐标轴m 上画出x(m) h(m)， x(m)和 h(m)以纵坐标为对称轴折叠成 h(-m)。 将h(m)以纵坐标为对称轴折叠成 h(-m)。 移位： h(-m)移位 移位n h(n-m)。 (2) 移位 ： 将 h(-m) 移位 n ， 得 h(n-m) 。 当 n 为 正数时，右移n 为负数时，左移n 正数时，右移n；当n为负数时，左移n。 相乘： h(n-m)和x(m)的对应序列值相乘 的对应序列值相乘。 (3)相乘：将h(n-m)和x(m)的对应序列值相乘。 相加：把所有的乘积累加起来，即得y(n) y(n)。 (4)相加：把所有的乘积累加起来，即得y(n)。