当前位置：文档之家 › 卷积计算图解法

卷积计算图解法

  • 格式：ppt
  • 大小：176.50 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

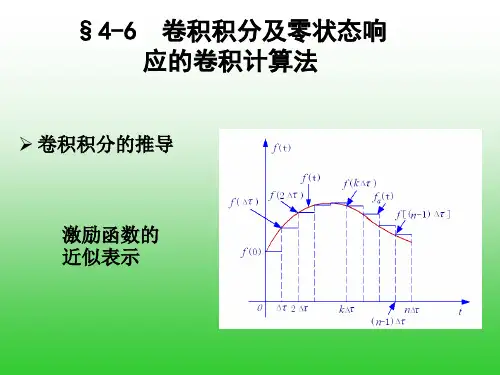
卷积积分及零状态响应的卷积计算法.

卷积积分及零状态响应的卷积计算法.

t
e RC
RCT
T RC t
e RCT 0
RC T RC
(t 0)
u0T T RC
e
t T
t
e RC
ε(t)
➢卷积积分的图解
求f(t)与h(t)的卷积，实质上是求一个新函数
f()h(t)在 由0到t的区间内的定积分。根据定积分的 几何意义，函数在0到t区间内的定积分值，决定于被积 函数f()h(t)的曲线在该区间内与 轴之间所限定的面
§4-6 卷积积分及零状态响 应的卷积计算法
➢ 卷积积分的推导
激励函数的 近似表示
f (t) fa (t) f (0)ε(t) ε(t )
f ( )ε(t ) ε(t 2 )
f (2 )ε(t 2 ) ε(t 3 )
f (n 1) ε(t (n 1) ) ε(t n )
解： [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
1 e t
0
(t 0)
(t 0)
1 1 e t ε(t)
例2 设图示RC串联电路中电压源的电压
t
u(t) u0e T ε(t)
求零状态响应电压uC(t)。
解： 用卷积积分公式求uC(t)，应先求冲激响应
如按
t
r(t) h( ) f (t ) d h(t) f (t)
0
当 0<t <1 时
计算。
r(t ) te ε( )d t e d 1 et
0
0
当 t >1时
r(t ) t e ε( )d t 1
t e d e(t1) et t 1 返回
注意ቤተ መጻሕፍቲ ባይዱ分上、下限

卷积计算(图解法)

卷积计算(图解法)

(1) n<0
x(m) m 0 4 h(n-m) m n-6 n0
y(n) = x(n) ∗ h(n) = 0
x(m) m
(2)在0≤n≤4区间上
0
4 h(n-m) m
n-6 0 n 4
∴ y(n) = ∑ x(m)h(n − m) = ∑1⋅ a
m=0 n m=0
n
n
n−m
=a
n
m=0
∑a
−m
1− a =a −1 1− a
n
−( n+1)
1− a =1− a
1+n
x(m)
(3)在4<n≤6区间上
m 0 4 h(n-m) m n-6 0
1+n
∴ y(n) = ∑x(m)h(n − m)
m=0
4
= ∑1⋅ a
m=0 n
4
n−m
=a
n
m=0
∑a
n−4
4
−m
4 6 n
1− a a −a =a = −1 1− a 1− a
−(1+4)
x(m) m 0 4 h(n-m) m 0 n-6
7
(4)在6<n≤10区间上
∴ y(n) = =
m=n−6
∑x(m)h(n − m)
=a
n m=n−6 −( 4+1)
n
m=n−6
∑1⋅ a
n
n
n−m
∑a
=
4
−m
6
n
10
=a
a
−( n−6)
−a −1 1− a
a
n−4
−a 1− a
综合以上结果， 可归纳如下： 综合以上结果，y(n)可归纳如下： 可归纳如下

§7.6 离散卷积(卷积和)

§7.6 离散卷积(卷积和)
X
第
y(n)的元素个数 的元素个数? 的元素个数
x(n) nA
d
6 页
h(n)
y(n)
nB
nC = nA + nB − 1
若：
x(n)序列
h(n)序列
n1 ≤ n ≤ n2，
n3 ≤ n ≤ n4
则y(n)序列
(n1 + n3 ) ≤ n ≤ (n2 + n4 )
4个元素 5个元素 8 个元素
X
例如： 例如：
x(n)： 0 ≤ n ≤ 3 h(n)： 0 ≤ n ≤ 4 y(n)： 0 ≤ n < 7
§7.6 卷积（卷积和） 卷积（卷积和）
卷积和定义 离散卷积的性质 卷积计算
第
一．卷积和的定义
状态响应： 回顾连续时间系统的零 状态响应： r(t ) = ∫ e(τ ) ⋅ h(t −τ )dτ
−∞ ∞
2 页
推导
= e(t ) ∗ h(t )
离散时间信号的分解： 离散时间信号的分解：
x : 任意序列 (n)表示为 (n)的加权移位之线性组合 δ
x(n) =
m=−∞
∑x(m)δ (n − m)
x(n) δ (n) h(n) y(n) h(n)
X
∞
问题：输出y(n)=？ 问题：输出 ？
第 3 页
时不变 均匀性 可加性 则输出： 则输出：
δ (n − m) →h(n − m)
x(m)δ (n − m) → x(m)h(n − m)
x(n) = y(n) =
X
第
三．卷积计算
x(n) ∗ h(n) =
∞ m=−∞
d
5 页
∑x(m)h(n − m)

卷积计算(图解法)

卷积计算(图解法)

m0
m0
n
an am
m0
an
1 a (n1) 1 a1
1 a1n 1 a
2021/3/11
5
x(m)
(3)在4<n≤6区间上
4
y(n) x(m)h(n m)
m0
m 04
h(n-m)
4
4
1 anm an am
m0
m0
m
n-6 0
46 n
an 1 a(14) an4 a1n
和 h(n)
0,
其它
a为常数，且1<a，试求x(n)和h(n)的卷积。
2021/3/11
2
解 参看图，分段考虑如下：
x(m)
n 04
h(m)
n 06
h(n-m)
(1)对于n<0；
n-6 n
(2)对于0≤n≤4；
(3)对于n>4，且n-6≤0，即4<n≤6；
(4)对于n>6，且n-6≤4，即6<n≤10；
1 a1
1 a
2021/3/11
6
x(m)
(4)在6<n≤10区间上
n
y(n) x(m)h(n m)
mn6
n
4
1 anm an am
mn6
mn6
an
a a (n6)
( 4 1)
1 a1
an4 a7 1 a
m 04
h(n-m)
m 0 6 10 n-6 n
2021/3/11
7
综合以上结果，y(n)可归纳如下：
正数时，右移n；当n为负数时，左移n。
(3)相乘：将h(n-m)和x(m)的对应序列值相乘。

计算卷积的方法.ppt

计算卷积的方法.ppt
' t
dg ( t ) r ( t ) e ( t ) h ( t ) e ( t ) dt
de (t) *g(t) dt
e ( t ) e ( t ) u ( t )
de ( t ) d ( e ( t ) u ( t ))de ( t ) u ( t ) e ( t ) ( t ) dt dt dt
方法一:

h (t )
t
e( )
0


*
0
h(t ) 非零值下限是－ 卷积分下限是零 u( ) 非零值下限是 0
h(t ) 非零值上限是 t 卷积分上限是 t u( ) 非零值上限是
若两个函数的左边界分别为tl1,tl2,右边界分别为 tr1,tr2,积分的 下限为max[tl1,tl2];积分的上限为min[tr1,tr2].


f f ( ) f ( t ) d 1 2 1 2 f
0 t-2 1
t
3 . if 1 t 2
1
b ab 2 ab 2 t a ( t ) d ( t ) 0 t 0 2 4 4
t
a t-2 0 t 1
ab (2 t 1 ) 4
2.各分段内卷积积分限的确定 。
分解成单位阶跃分量之和
f (t1 )
f( t t ) 1 1 f ( 0)
t1
t1
u ( t ) g ( t ) DaHarma ln tegr
*.Duharmal integral
r(t) e(0 )g(t) e ( )g(t )d 0
1
b ab 2 1 f f a ( t ) d ( t ) 1 2 0 02 4

第二章第3讲 卷积

第二章第3讲 卷积



[ f () * f ()]d f (t) * f ()d f (t) * f ()d
1 2 1 2 2 1
t
t
t
证明：

[ f ( ) * f
1 t 1
t
2
( )]d [ f1 ( ) f 2 ( )d ]d
[ f1 (t )u(t t1 )] [ f 2 (t )u(t t2 )]
信号与系统 同济大学汽车学院 魏学哲 weixzh@
g (t ) f1 ( )u( t1 ) f 2 (t )u(t t2 )d


结合律应用于系统分析,相当于串联系统的冲激响 应,等于串联的各子系统冲激响应的卷积
信号与系统 同济大学汽车学院 魏学哲 weixzh@
卷积的微分与积分
df2 (t ) df1 (t ) d [ f1 (t ) * f 2 (t )] f1 (t ) * f 2 (t ) * dt dt dt

t t2
t1
f1 ( ) f 2 (t )d
t1 t t2
t
积分限是： 例：
f1(t ) 2e u(t )
g (t )

f 2 (t ) u(t ) u(t 2)
求
f1 ( ) f 2 (t )d
信号与系统 同济大学汽车学院 魏学哲 weixzh@
f1( ) 1 f2(1-) 2
f1( ) 1 f2(2-) 2
f1( )
f2(3-)
2
c
c
c
c
-1
0

f1() f2(-)

信号第二章3卷积

信号第二章3卷积


若将此信号作用到冲激信号为h(t)的线性时不 变系统，则系统的响应为
r (t ) H [e(t )] H [ e( ) (t )d ]


e( ) H [ (t )]d


e( )h(t )d

零状态响应：rzs (t ) e( )h(t )d h(t ) e(t )
def
2.算子符号基本规则
(1)算子多项式可以进行因式分解 ( p 2)( p 3) p 2 5 p 6 例如： (2)等式两端的算子符合因式不能相消 ( p 2) r (t ) ( p 1) e(t ) ( p 2)( p 3) r (t ) ( p 2 4 p 3) e(t ) 不能简化为： (3)算子的乘除顺序不能随意颠倒
（3）结合律： f1(t) f2 (t) f3 (t) f1(t) f2 (t) f3 (t)
e(t)
h1(t)
h2(t)
r(t)
串联系统 r (t ) e(t ) h1 (t ) h2 (t )
2.卷积的微分与积分
d f1 (t ) f 2 (t ) df 2 (t ) （4）微分性： f1 (t ) dt dt df1 (t ) (适于高阶微分） f 2 (t ) dt

r (t ) e( )h(t )d


1 (a) t 2
e(t ) * h(t ) 0
h(t )
e( )
1
1 2
t 2
(b)
0
1 t 1 2
相乘
t
1
1 t 1 2 t 1 e(t ) * h(t ) 1 1 (t )d 2 2 t2 t 1 4 4 16 (b)

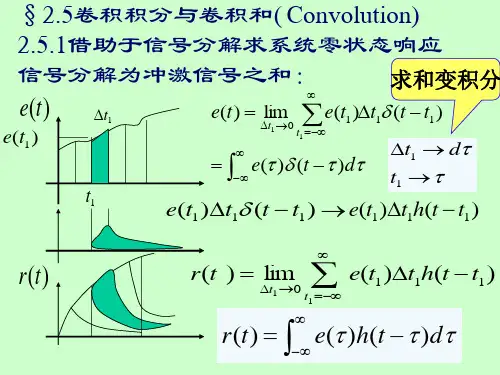
与冲激函数或阶跃函数的卷积

与冲激函数或阶跃函数的卷积


表明：LTI系统对任意激励信号e(n)的零状态响 应r(n)等于e(n)与单位样值响应的卷积和。
（1）对因果序列
r (n) e(n) * h(n)
k
e(k )h(n k )
0 k n

k 0, e(k ) n k 0 k n, h(n k ) 0
f1 (t t1 ) * f 2 (t t2 ) s(t t1 t2 )
3.3 卷积和定义
r ( n) e( n) * h( n)
3.4 图解法、列表法、解析法
k
e(k )h(n k )
•L=L1+L2-1

作业：1-9, 2-1(1) ,2-3, 2-15(2),2-16(1) 作业：2-4(1) (3)
r ( n)

k n
e(k )u(k )h(n k )u(n k )
k 0
e( k ) h ( n k )
(2)任意两个序列的卷积和
f (n) f1 (n) f 2 (n)
k
f (k ) f
1

2
(n k )
满足交换律、分配率、结合律
f1 (t ) * f 2 (t ) * (t t1 ) * (t t2 ) s(t ) * (t t1 t2 ) s(t t1 t2 )
（2）与冲激偶‘（t）的卷 积
卷积的微分性质
f (t ) * ' (t )
f ' (t ) * (t ) f ' (t )
t1 0
t1
e(t )t (t t )

卷积积分的步骤

卷积积分的步骤

卷积积分的步骤
卷积积分图解法的步骤依次为:1.换元；2.翻转；3.平移；4.相乘；5.积分。

卷积积分图示法的五个步骤：
1、公式如下：卷积积分公式是（f *g）∧（x）=(x)·(x)，卷积是分析数学中一种重要的运算。

2、设f（x），g（x）是R1上的两个可积函数，作积分，可以证明，关于几乎所有的x∈（－∞，∞），上述积分是存在的。

3、这样，随着x的不同取值，这个积分就定义了一个新函数h(x)，称为f与g的卷积，记为h（x）=（f *g）（x）。

4、容易验证，（f *g）（x）=（g *f）（x），并且（f *g）（x）仍为可积函数。

卷积与傅里叶变换有着密切的关系。

6、以(x) ，(x)表示L1（R）1中f和g的傅里叶变换，那么有如下的关系成立：（f *g）∧（x）=(x)·(x)，即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换。

7、这个关系，使傅里叶分析中许多问题的处理得到简化。

8、由卷积得到的函数（f *g）（x），一般要比f，g都光滑。

9、特别当g为具有紧支集的光滑函数，f 为局部可积时，它们的卷积（f *g）（x）也是光滑函数。

10、利用这一性质，对于任意的可积函数，都可以简单地构造出一列逼近于f 的光滑函数列fs（x），这种方法称为函数的光滑化或正则化。

11、卷积的概念还可以推广到数列、测度以及广义函数上去。

卷积积分介绍

卷积积分介绍

h(t)
(1) 1
O
(1) t
g(t)
1
O12 1
g(t)f(1)(t)h(1)(t)
t 3 2t
t 3
0t 1 1t 2 2t 3
3 t
注意
28
注意
当f1(t)
t df1(t)dt时, dt
f 1 ( t) f 2 ( t) f 1 ( t) f 2 ( 1 )( t)
例 sg t： n t
系统并联运算
3．结合律
f ( t ) f 1 ( t ) f 2 ( t ) f ( t ) [ f 1 ( t ) f 2 ( t )]
系统级联运算
22
系统并联
f 1 ( t ) [ f 2 ( t ) f 3 ( t ) f ] 1 ( t ) f 2 ( t ) f 1 ( t ) f 3 ( t ) 系统并联，框图表示：
一般数学表示： g(t) f1()f2(t)d 信号无起因时： g(t) f()h(t)d
(4)卷积是数学方法，也可运用于其他学科 。
(5)积分限由 f1(t),f2(t)存在的区间决定，即由
f1()f2(t)0的范围决定。
20
总结
求解响应的方法： 时域经典法： 完全解=齐次解 + 特解 双零法：
: 信号作用的时刻，积分变量
从因果关系看，必定有 t
(2)分析信号是手段，卷积中没有冲激形式，但有其内容；
f() 是h(t-)的加权，求和
即d f() 是h(t-)的加权，积分
(t-)的响应
19
(3)卷积是系统分析中的重要方法，通过冲激响应h(t)建 立了响应r(t)与激励e(t)之间的关系。
零输入响应：解齐次方程，用初（起）始条件求系数；

卷积

卷积

1 1 2
1 (t ) d 2
t2 t 1 4 4 16
h(t ) 1
1 2
(c ) 1 t
3 2
1
0
t 1
3 2

(c ) 1 t
1 e(t ) * h(t ) 1 1 (t )d 2 2 3 3 t 4 16
X
第 12 页
第 14 页
X
。
• 练习
已知
1 f1 ( t ) 0 t 1 t 1 t f 2 (t ) 2 ( 0 t 3)
第 15 页
求卷积。
解：
t t 1 4 2 4 t g( t ) 2 t t 2 4 2 0
2
g (t )
1 2
1
0(a) t Nhomakorabeat
1 (a) t 2
1
e(t ) * h(t ) 0
X
第 11 页
h(t )
1 2
e( )
1
1 (b) t 1 2

e(t ) * h(t )
1t (b) t 1 2
e( )
0
1

t

§2.６卷积
•卷积
•利用卷积积分求系统的零状态响应
•卷积图解说明
•卷积积分的几点认识
第
一．卷积（Convolution）
设有两个 函数
2 页
f1 (t ) f 2 (t ) ，积分
f (t ) f1 ( ) f 2 (t ) d


称为
f1 (t ) f 2 (t ) 的卷积积分，简称卷积，记为

第二章卷积图解计算

第二章卷积图解计算
卷积积分的图解计算
计算 f (t) = f1(t) ∗ f2 (t) = ∫−∞ f1(τ ) f2 (t −τ )dτ
( ff1τt)) 1(
() ff22(τt)
1 1 2 2
步骤
∞
将f2 (τ )反 得f2 (− ) 折 τ
f2 (−τ)
1 2
1 1
0 0
1 1
t
f1(τ )
0 τ 0
1 1
2 2
1Байду номын сангаас
0
1 +t −3
−1+ t
τ
−1+ t
f2 (t −τ )
1 2
0
τ
平移
第二章第1讲
1
例
1
计算 f (t) = f1(t) ∗ f2 (t) = ∫−∞ f1(τ ) f2 (t −τ )dτ
当 −1+ t < 0 即 t < 1 时： f 2 (t −τ ) 和 f1 (τ ) 没有公共的重叠部分， 1 2 故卷积 f (t) = f1 (t) ∗ f2 (t) = 0 t 0 1 2 3
1 1 1× dτ = (4 − t) −3+t 2 2
1
即为重叠部分的面积。 当 −3+t ≥1 即 t ≥ 4 时： f 2 (t −τ ) 和 f1 (τ ) 没有公共的重叠部分， 故卷积 f (t) = f1 (t) ∗ f2 (t) = 0
第二章第1讲 3
f 2 (t −τ ) f1(τ)
4
f (t)
∞
f 2 (t −τ ) f1(τ)
1
−3 + t −1+ t 0
1

卷积图解法

卷积图解法
b
* 0 -1 1 1 b f1 a[u(t ) u(t 1)]t t f 2 (t 1)[u (t 1) u (t 1)] j 2 2 2 f 2 f1 f 2 ( ) f1 (t ) du (t ti t j )
i 1 j 1 ti
p q i 1 i
j 1

i 1 j 1
f (t )h (t )[u( t )u(t t
j i
j
)]d
由以上讨论可知:
得出卷积积分的上下限和定义域如下:
f h

i 1 j 1
p
q
t t j
f i ( ) h j (t ) du (t t i t j )


u ( 1)u (t 2)d u ( 1)u (t 3)d
t 2


d d (t 2 1) (t 3 1) 1
1
t 2
t 3
1

du (t 2 1) du (t 3 1)
e ( ) g (t )d
'
t
0

预习§2.7 作业 p85 2-19
(a),(b),(f)
1 1
t 3
(t 3)u (t 3) (t 4)u (t 4)
*. *.快速定限表 若参与卷积的两个函数fs(t)和fl(t)都是只有一个定义段,它 们的时限长度分别为TS和TL,并且TS< TL,长函数fl(t)的左 右时限分别为LL和RL,而短函数fs(t)的的左右时限分别为LS 和RS,并规定积分号内括号统一只表示 f s ( ) f l (t ) 即只反 转时限长的函数. rs

信号与系统第二章(3)卷积积分

信号与系统第二章(3)卷积积分

y(t) 1 f1(τ ) f2( t - ) τ y(3)
0 (e) t >3
3
t
τ
0 (f )
3
t
例2 求下图所示函数 f1(t )和 f2 (t )的卷积积 分.
2
f1 (t ) f 2 (t )
3 4
2
0 2
2
f1 (τ )
t
0
2
f 2 ( τ )
3 4
t
解(1) )
2
0
2
τ -2
0
τ
(2) )
由前面分析知: 由前面分析知:
y zs (t ) = ∫ f (τ )h(t τ )dτ
0
tHale Waihona Puke = f (t ) h(t )
这是求解零状态响 应的另一种方法. 应的另一种方法
二,卷积的图示法
第一步, 波形,将波形图中的t轴 第一步,画出 f 1 ( t ) 与 f 2 ( t ) 波形,将波形图中的 轴 ) 改换成τ轴 的波形. 改换成 轴,分别得到 f1 ( τ) f 2 ( τ的波形. 和 第二步, 波形以纵轴为中心轴翻转180° 第二步,将 f 2 (τ)波形以纵轴为中心轴翻转180°, 波形. 得到 f 2 ( τ)波形. 第三步,给定一个t值 波形沿τ轴平移 轴平移|t|. 第三步,给定一个 值,将 f 2 ( τ) 波形沿 轴平移 . 在t<0时, 波形往左移;在t>0时,波形 时 波形往左移; 时 往右移. 的波形. 往右移.这样就得到了 f 2 ( t τ) 的波形.
2
2
-1
0
t
f2 (t )
1
-1
0
1

卷积积分介绍

卷积积分介绍

h(t)
(1) 1
O
(1) t
g(t)
1
O12 1
g(t)f(1)(t)h(1)(t)
t 3 2t
t 3
0t 1 1t 2 2t 3
3 t
注意
28
注意
当f1(t)
t df1(t)dt时, dt
f 1 ( t) f 2 ( t) f 1 ( t) f 2 ( 1 )( t)
例 s g t： n t
波形
e t
1
e2t u(t)u(t2)
ht
1
et u(t )
O
2t
it
O
2
O
t
分段表示：
i(t) 2(e2t et ), 2e(t1) et ,
0t 2 t 2
t
7
卷积的图解说明
用图解法直观，尤其是函数式复杂时，用图形分段求
出定积分限尤为方便准确，用解析式作容易出错，最好将
两种方法结合起来。
f(t)k(t)fk(t)
f( t)k ( t t0 ) fk ( t t0 )
27
例2-7-1 已 f t ,h t 知 ， g t f 求 t h t 。
f (t) 1
h(t) 1
O 12 t 1
f 1(t) 1
O 12 t
f (1)()
h(tt1)1
tO 1
1
2
O 1t
一般规律： f1t
下限 [A,B]
f1t -1 1
f2t [C,D]
+ f2t 0 3
gt [A+C,B+D]
gt 1 4
当 f1t或 为f2非t连续函数时，卷积需分段，积分限分段定。

计算卷积的方法

计算卷积的方法

.某复合系统如图所示 ,两个子系统的冲激响应 分别为 h1 (t ) u (t ), h2 (t ) u (t 1) u (t 2) 1. 求该系统的冲激响应 h(t). 2. 当系统的输入 f(t) ' (t )时,求该复合系统的零状态 响应y zs (t ).

f(t)
tj0tj1f1f21快速定限表若参与卷积的两个函数fst和flt都是只有一个定义段它们的时限长度分别为ts和tl并且tstl长函数flt的左右时限分别为ll和rl而短函数fst的的左右时限分别为lsrs并规定积分号内括号统一只表示即只反转时限长的函数
*计算卷积的方法
1.用图解法计算卷积
分段时限
2.用函数式计算卷积 3.利用性质计算卷积
b
* 0 -1 1 1 b f 2 (t 1)[ u (t 1) u (t 1)] f1 a[u(t ) u(t 1)] t t j 2 2 2 f 2 f1 f 2 ( ) f1 (t ) du (t ti t j )
i 1 j 1 ti
t
b
0
f2(t)
解:1. t 0
0
2
t-2 0 1 t a t-2 0 1
重合面积为零:f1(t)*f2(t)=0
2.if 0 t 1


f1 f 2 f1 ( ) f 2 (t )d
0 t-2 1
t
3.if 1 t 2
1
b ab a (t )d (t ) 2 0 2 4
e(t )
h2 (t )
h1 (t )
h3 (t )

r (t )

卷积积分及零状态响应的卷积计算法.

卷积积分及零状态响应的卷积计算法.

如按式
t
r(t)
f (t) h(t) 0
f ( )h(t ) d
计算。
如按式
t
r(t) 0 h( ) f (t ) d h(t) f (t)
计算。
例3 图示某电路的激励函数与冲激响应。求电路的零状态响应。
如按
t
r(t) f (t) h(t) 0 f ( )h(t ) d
δt
f
t
t
0
δ
f
t
d
0δ f 0
t d
f
t
δt f t f t
f tδt f t
δt
t0
f
t
t
0
δ
t 0
f
t
d
δ t0
t0
t0
f
t
d
f t t0
例1 求卷积 [e tε(t)] ε(t)
解： [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
f ( )ε(t ) ε(t 2 )
f (2 )ε(t 2 ) ε(t 3 )
f (n 1) ε(t (n 1) ) ε(t n )
n1
f (k )ε(t k ) ε(t (k 1) ) k0
f (t) fa(t)
n1 k0
f
(k )ε(t
k )
1 e t
0
(t 0)
(t 0)
1 1 e t ε(t)
ቤተ መጻሕፍቲ ባይዱ
例2 设图示RC串联电路中电压源的电压
t
u(t) u0e T ε(t)
求零状态响应电压uC(t)。
解： 用卷积积分公式求uC(t)，应先求冲激响应
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

m 04
h(n-m)
m
n-6 0 n 4
n
n
y(n) x(m)h(nm) 1anm
m0
m0
anmn0aman1 1a a( n11)
1a1n 1a
x(m)
(3)在4<n≤6区间上
m
4
y(n) x(m)h(n m) m0
04 h(n-m)
4
4
1 anm an am
m0
m0
m
n-6 0
卷积计算——图解法
y(n) x(m )h(nm )x(n)h(n) m
计算步骤如下： (1)翻褶：先在坐标轴m上画出x(m)和h(m)，
将h(m)以纵坐标为对称轴折叠成 h(-m)。 (2)移位：将h(-m)移位n，得h(n-m)。当n为
正数时，右移n；当n为负数时，左移n。 (3)相乘：将h(n-m)和x(m)的对应序列值相乘。 (4)相加：把所有的乘积累加起来，即得y(n)。
综合以上结果，y(n)可归纳如下：
0,
1
a 1 n
,
1 a
y(n)
a
n4 a 1n 1 a
,
a n4 a7
1 a
,
0 ,
n0 0n4 4n6 6 n 10 10 n
n-6 n
(2)对于0≤n≤4；
(3)对于n>4，且n-6≤0，即4<n≤6；
(4)对于n>6，且n-6≤4，即6<n≤10；
(5)对于(n-6)>4，即n>10。
(1) n<0
x(m)
y(n )x(n ) h (n ) 0 0 4
m
h(n-m)
m n-6 n 0
x(m)
(2)在0≤n≤4区间上
46 n
an 1 a(14) an4 a1n
1 a1
1 a
x(m)
(4)在6<n≤10区间上
m 04
n
y(n) x(m)h(n m)
h(n-m)
mn6
n
4
1 a nm a n a m
m 0 6 10 n-6 n
mn6
mn6ห้องสมุดไป่ตู้
an
a (n6) a (41) 1 a 1
an4 a7 1 a
计算卷积时，一般要分几个区间分别加以 考虑，下面举例说明。
例 已知x(n)和h(n)分别为：
1, 0n4 x(n)0, 其它
和
an, 0n6 h(n)0, 其它
a为常数，且1<a，试求x(n)和h(n)的卷积。
解 参看图，分段考虑如下：
x(m)
n 04
h(m)
n 06
h(n-m)
m
(1)对于n<0；