下载文档原格式
杆件的基本变形形式
杆件的基本变形形式有以下几种：
1. 拉伸和压缩：当杆件受到沿其轴向的力时，杆件会发生拉伸或压缩变形。
拉伸时杆件长度增加，压缩时杆件长度减小。
2. 剪切：当杆件受到垂直于其轴向的力时，杆件会发生剪切变形。
剪切变形表现为杆件的横截面发生相对错动。
3. 扭转：当杆件受到绕其轴线的力矩时，杆件会发生扭转变形。
扭转变形使得杆件的横截面绕轴线旋转。
4. 弯曲：当杆件受到垂直于其轴线的横向力时，杆件会发生弯曲变形。
弯曲变形导致杆件的轴线发生弯曲。
这些基本变形形式是杆件在不同加载条件下的主要响应方式。
在工程和力学领域中，了解杆件的基本变形形式对于设计和分析结构非常重要。
通过对这些变形形式的研究，可以确定杆件在负载下的应力、应变分布以及可能的破坏模式。
需要注意的是，实际工程结构中的杆件可能同时受到多种变形形式的组合作用。
例如，在一个梁的设计中，可能同时存在弯曲和剪切变形。
因此，在分析杆件的变形和应力时，需要综合考虑各种变形形式的影响。
希望这些信息对你有所帮助！如果你有其他问题，请随时提问。
第2章 杆件的拉伸与压缩提要：轴向拉压是构件的基本受力形式之一，要对其进行分析，首先需要计算内力，在本章介绍了计算内力的基本方法——截面法。
为了判断材料是否会发生破坏，还必须了解内力在截面上的分布状况，即应力。
由试验观察得到的现象做出平面假设，进而得出横截面上的正应力计算公式。
根据有些构件受轴力作用后破坏形式是沿斜截面断裂，进一步讨论斜截面上的应力计算公式。
为了保证构件的安全工作，需要满足强度条件，根据强度条件可以进行强度校核，也可以选择截面尺寸或者计算容许荷载。
本章还研究了轴向拉压杆的变形计算，一个目的是分析拉压杆的刚度问题，另一个目的就是为解决超静定问题做准备，因为超静定结构必须借助于结构的变形协调关系所建立的补充方程，才能求出全部未知力。
在超静定问题中还介绍了温度应力和装配应力的概念及计算。
不同的材料具有不同的力学性能，本章介绍了塑性材料和脆性材料的典型代表低碳钢和铸铁在拉伸和压缩时的力学性能。
2.1 轴向拉伸和压缩的概念在实际工程中，承受轴向拉伸或压缩的构件是相当多的，例如起吊重物的钢索、桁架第2章 杆件的拉伸与压缩 ·9··9·2.2 拉(压)杆的内力计算2.2.1 轴力的概念为了进行拉(压)杆的强度计算，必须首先研究杆件横截面上的内力，然后分析横截面上的应力。
下面讨论杆件横截面上内力的计算。
取一直杆，在它两端施加一对大小相等、方向相反、作用线与直杆轴线相重合的外力，使其产生轴向拉伸变形，如图2.2(a)所示。
为了显示拉杆横截面上的内力，取横截面把m m −拉杆分成两段。
杆件横截面上的内力是一个分布力系，其合力为N F ，如图2.2(b)和2.2(c)所示。
由于外力P 的作用线与杆轴线相重合，所以N F 的作用线也与杆轴线相重合，故称N F 为轴力(axial force)。
由左段的静力平衡条件0X =∑有：()0+−=N F P ，得=N F P 。
简述杆件变形的四种基本形式杆件变形是指在外力作用下，杆件的长度、形状或尺寸发生改变的现象。
在工程学中，杆件变形是一个重要的研究内容，主要用于结构分析、设计和优化。
杆件变形的四种基本形式可以分为以下几类：1.延伸变形：延伸变形是指杆件在受到拉力作用时，其长度发生变化的形式。
在受到拉力作用时，杆件会发生“伸长”的现象。
延伸变形可以通过胡克定律来描述，即拉力与伸长量成正比。
具体而言，如果拉力作用于杆件上，则杆件产生的伸长量与拉力的比例为常数，该比例常数称为弹性模量。
延伸变形的产生原因主要有杆件被拉伸、受到温度变化引起的热应变和径向引力等。
2.压缩变形：压缩变形是指杆件在受到压力作用时，其长度发生变化的形式。
与延伸变形类似，杆件在受到压力作用时会发生“缩短”的现象。
压缩变形可以通过胡克定律来描述，即压力与压缩量成正比。
压缩变形的原因主要有杆件被压缩、受到温度变化引起的热应变和径向引力等。
3.弯曲变形：弯曲变形是指杆件在受到弯矩作用时，沿长度方向发生弯曲的形式。
当外力作用在杆件的中部时，中部会发生弯矩，使得杆件在这一区域产生弯曲变形。
弯曲变形可以通过伯努利梁理论来描述，该理论基于假设杆件在变形过程中横截面的变形很小，可以近似为平面内曲线的弯曲变形。
弯曲变形的产生原因主要有集中载荷、均匀分布载荷和温度变化引起的热应变等。
4.扭转变形：扭转变形是指杆件在受到扭矩作用时，沿长度方向发生扭转的形式。
当外力作用在杆件的两端时，两端产生扭矩，使得杆件在这一区域产生扭转变形。
扭转变形可以通过剪切应力与剪切变形之间的关系来描述。
扭转变形的产生原因主要有转矩、剪切力和温度变化引起的热应变等。
除了以上四种基本形式外，杆件还可能发生复杂的组合变形，如弯曲-延伸变形、扭转-延伸变形等。
不同形式的杆件变形在工程设计中都需要进行准确的分析与计算，以确保结构的稳定性和安全性。
材料力学基本概念及计算公式杆件的拉伸与压缩部分1、拉伸与压缩的受力特点：作用于杆件两端的力大小相等，方向相反，作用线与杆件的轴线重合。
2、拉伸与压缩的变形特点：杆件沿轴线方向伸长或缩短。
3、拉伸与压缩变形的内力：称为轴力，用符号N F 表示。
杆件在外力作用下，其内部的一部分对另一部分的作用。
4、求内力的方法：截面法。
截开→代替→平衡（截→代→平）5、横截面上的应力正应力：与横截面垂直，用符号σ表示，计算公式为AF N =σ，正应力的单位为2/m N N F 为该横截面上的内力，单位为N ，A 为横截面的截面积,单位为2m 。
Pa m N 1/12=，MPa m N 1/10126=⨯,GPa m N 1/10129=⨯ 正应力σ符号规定与轴力相同，拉应力为正，压应力为负。
切应力：在横截面内，与正应力垂直，用符号τ表示，单位为2/m N 。
6、拉压变形与胡克定律绝对变形：表示杆沿轴向伸长（或缩短）的量，用L ∆表示。
相对变形：表示单位原长杆件变形的程度，用ε表示，也称线应变。
LL ∆=ε 胡克定律：表明杆件拉伸与压缩时，变形和应力之间的关系。
胡克定律的内容：当杆件内的轴力N F 不超过某一限度时，杆的绝对变形量L ∆与轴力N F及杆长L 成正比，与杆的截面积A 成反比。
AE LF L N ⨯⨯=∆ E ；表示材料的弹性模量，表示材料抵抗拉压变形能力的一个系数。
EA ：表示杆件的抗拉压刚度，表示材料抵抗拉压变形能力的大小。
7、许用应力和安全系数许用应力：危险应力0σ除以大于1的系数n 表示，用符号][σ表示，计算公式为n 0][σσ=脆性材料：b bn σσ=][，塑性材料：s s n σσ=][s σ表示塑性材料的屈服点应力值，b σ表示脆性材料的强度极限应力值。
安全系数：大于1的系数，用n 表示。
s n 表示塑性材料的安全系数值，b n 表示脆性材料的安全系数值。
8、拉伸与压缩的强度计算 强度计算公式：][σσ≤=AF N 可以解决三类问题：（1）强度校核：][σσ≤=A F N （2）选择截面尺寸：][σN F A ≥ （3）确定许用载荷：A F N ⨯≤][σ材料力学基本概念及计算公式剪切与挤压部分1、 剪切的受力特点：作用在构件两侧面上的外力的合力大小相等，方向相反，作用线平行且相距很近。
第2章杆件的拉伸与压缩杆件的拉伸与压缩是杆件的基本变形形式之一,也是最简单的一种变形形式。
本章主要通过对于拉伸与压缩的研究,我们将对杆件变形与内力的关系以及材料基本力学性质的研究建立初步的概念。
因此,对拉伸与压缩的研究具有重要的意义。
本章将建立拉压杆内力的概念和应力、应变的概念,讨论截面法在求解拉压杆内力中的具体应用,研究应变与应力的关系及材料拉伸压缩时的力学性能,建立强度计算的基本概念,并对超静定问题的求解作初步的了解。
§2.1引言在实际工程中,我们经常会遇到承受轴向拉伸和轴向压缩的等直杆件。
例如组成起重机塔架的杆件(图 2.l),房屋的屋盖珩架中的杆件(图 2.2)等。
如图 2.2(a)所示的房屋的屋盖椅架,是由很多等直杆件绞接而成的。
现取出拉杆和压杆来进行分析。
拉杆的计算简图如图 2.2(c),它是一根受拉的等直杆,由节点处传来的合力 P, 作用在杆件的两端,与杆的轴线重合,并且大小相等方向相反,它们使杆件产生轴向的伸长变形,我们称之为轴向拉伸;作用在压杆图 2.2(b)两端的力 P使杆产生轴向压缩变形,称为轴向压缩。
图 2.l 图 2.2 (a) 图2.2(c)(b) 拉杆和压杆通过上述实例得知轴向拉伸和压缩具有如下特点：受力特点: 作用于杆件两端的外力大小相等，方向相反，作用线与杆件轴线重合，即称轴向力。
变形特点: 杆件变形是沿轴线方向的伸长或缩。
§2.2 用截面法计算拉(压)杆的内力一、拉(压)杆内力的概念内力的概念:杆件在受到轴向拉力作用时,会产生变形而伸长,同时,在杆件内任何截面处,截面两侧相连部分之间产生相互作用力,它的存在保证了截面两侧部分不被分开,这种作用力就是杆件的拉伸内力。
类似地,杆件在受到轴向压力作用时,杆件内部会产生压缩内力。
二、用截面法求轴力根据 1.5 节所介绍计算杆件内力的方法即截面法的原理和一般步骤,现在研究拉(压)杆的内力计算方法。
图 2.3(a)所示拉杆,两端各作用一轴向外力P,内力的计算步骤如下:(1)在该杆任一横截面 m-m 处将其假想地切开,取其左半部分(或右半部分)为脱离体。
（2)对所取脱离体作受力分析,画出受力图。
该脱离体除原来受到的外力 P 之外,在横截面 m-m 处还受到右半部分对它的作用力。
我们已经指出,这种作用力本来是分布在整个截面上的连续分布力,在计算内力时,只考虑它们的合力。
设其合力为 N,并设其方向为背离截面方向,即设其为拉力。
则脱离体的受力分析如 图 2.3(b )的所示。
(3) 对所取脱离体列出平衡方程 由平衡条件得，由于（拉力），则，如图 2.3(b)所示。
对B 段也有:，'N =P ，'N =N 如图 2.3(c) 所示这样,即解得截面 m-m 处的内力。
上述方法也同样适用于如图 2.4 所示的受压杆的内力计算,此时将求得 N=-P,负号表明N 的实际方向与所设方向相反。
显然,为了保证脱离体的平衡,N 的作用线必然与P 的作用线重合,也就是说,内力N 是沿杆件轴线作用的。
因此我们把轴向拉 (压)杆的内力称为轴力。
轴力的符号规定:规定拉力为正的轴力,而压力则为负的轴力。
在用截面法计算轴力时,为图 2.3'N x(c)(b)(a)了避免符号上的混乱,一般总是设轴力为拉力,如果计算结果为正值,表明实际轴力为拉力,与所设相同; 如计算结果为负值,则表明实际轴力为压力。
三、轴力图1、轴力图轴向拉 (压)杆上各部分的轴力将依所受荷载而变化 , 可以用图形来直观地表明杆件上各截面处轴力的变化情况,这种图形叫做 “ 轴力图 ”。
该图一般以杆轴线为横坐标表示截面位置，纵轴表示轴力大小，以下通过一个例子来说明轴力图的作法。
2、举例图 2.5（a ）所示杆承受三个轴向外力。
由于在截面 B 处作用有外力,当在B 截面以左或以右用截面截开杆件,截取的脱离体受力情况是不同的。
也就是说,B 截面以左和以右的杆段轴力是不同的,因而需要分段研究。
用截面法先计算AB 段的轴力。
在 AB 段的任一横截面 1-1 处将杆切开,并选左段脱离体为研究对象,其受力情况如图 2.5(b) 所示。
由平衡方程图 2.4(b)(a)m0201==P N X -∑，由得, AB 段的轴力为 N 1=2P.对于 BC 段,仍用截面法,在任一横截面2-2 处将其切开,仍选左段研究其平衡,如图 2.5(c)所示,有0202=+=P P NX -,∑ , P N =2.实际上往往不需要先列平衡方程再求解，可直接求BC 段上的轴力,P P P N ==-22.若取2-2截面以右为脱离体,仍可得P N =2,可见整个杆上各截面处轴力不同.结论:杆任一横截面上的轴力值等于该截面任一侧的杆上所有轴向外力的代数和,与内力(方向假定)方向相反的外力为正,相同的外力为负,即iii P N ∑= 绘制轴力图: 为表达截面位置选x 轴为横坐标，相应截面上的轴力为纵坐标，根据适当比例，绘出轴力图,如图 2.5(e),由图可知 AB 段的轴力值最大，N max =2P .[例2.1] 绘制下图阶梯杆的轴力.[解] 截面顺序从右往左排列,取截面以右的各段为隔离体.1()a()b()c （d)（e)图 2.5)(---max 在第一段P N P P P P N P P P N P N 3234233321==+==-==说明: 绘轴力图时,中间直线和坐标箭头可以去掉.四、应力的概念前面已指出,轴力是截面上分布内力的合力。
为了研究拉(压)杆横截面、斜截面上内力分布规律,需要引进应力的概念。
点的应力的概念：在外力作用下,杆件内力在截面上某点分布内力的集度称为该点的应力。
平均应力：如图2.7所示,在截面 m-m 上任取一点（K ）的周围取一微小面积A ∆, 设在∆A 上的分布内力的合力为∆P, 则∆P 与A ∆的比值AP∆∆代表A ∆内的分布内力的平均集度,称之为A ∆内的平均应力。
当A ∆趋向于零时这个平均应力的极值就是 K 处的应力p ，即dA dP A PA p ==∆∆→∆lim 0(2.1)图 2.6的极限方向；是一个矢量，方向是P p ∆.,,:aaaMP kP m N P p ）（的单位2-⋅五、横截面上的应力要确定拉(压)杆横截面上的内力分布规律,即确定横截面上各点的应力,仅靠平衡条件是不能解决的。
杆件在外力作用下不仅产生内力,而且引起变形,内力和变形之间总是相互关联的。
要研究应力分布问题 , 除应利用平衡条件外,还应考虑杆件的变形,并利用内力和变形间的关系建立必要的补充条件。
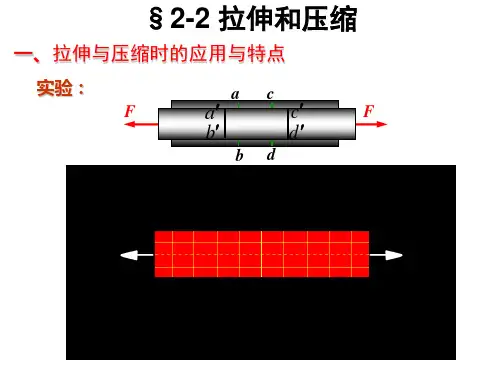
现通过试验观察拉(压)杆的变形情况:图2.8(a) 为一等截面直杆,试验前,在杆件表面等问距地画上与杆轴平行的纵线以及与杆轴垂直的横线, 然后,在杆件两端施加轴向外力P 。
由图2.8(b)可见,在施加外力之后,各纵、横线仍为直线,并分别平行和垂直于杆轴,只是横线间的距离增加,所有的原纵横线形成的正方形网格均变成大小相同的长方形。
1、 平面假设根据上述现象,对轴向拉(压)杆内部的变形作如下假设: 变形后,横截面仍保持为平面, 并且仍垂直于杆轴,只是各横截面沿杆轴作相对平移,此假设称为平面假设。
如果将杆件设想成由元数根纵向“ 纤维 ”所组成,则由平面假设可知,任意两横截面间的所有纤维的变形均相同。
由于已经假定材料是均匀的,各纵向纤维变形相同,意味着受力也相同,由此可见 ,横截面上各点处的应力相等,其方向均垂直于横截面[图2.8(c)]。
垂直于横截面的应力称为正应力或法向应力,用σ表示。
若拉(压)杆横截面积为 A, 轴力为 N, 则正应力为AN=σ (2.2)图2.7由公式(2.2)可知,正应力的符号随轴力的符号而定， 即拉应力为正 , 压应力为负。
2、由静力平衡条件确定的大小由于，所以积分得则上式中：-横截面上的正应力，-横截面上的轴力，-横截面面积。
正应力的正负号规定为：拉应力为正，压应力为负。
[例2.2] 求右图中应力的最大值，设杆件的截面积为 A=400mm 2。
[解]AN maxmax σ=由公式： 又由内力图可知，kN N 50=maxkN55kN40kN25kN50σ(c)图 2.8(b)(a)所以a a P MP 662310125125101041050⨯==⨯⨯⨯=maxσ六、斜截面上的应力1. 斜截面上的总应力现在研究杆的任意斜截面上的应力。
如图 2.9(a) 所示, 用一个与横截面成α角的斜截面走假想地将杆截分为二 , 并研究左段杆图 2.9(b)的平衡。
于是得到此斜截面上的内力Pa 为:αααA p P P ==αp 为k-k 斜截面上的总应力，由平面假设(拉伸时斜截面αp 平行移动)知,斜截面上的应力也是均匀分布的,故αααA P p =而，所以AP=0σ 为拉杆横截面上的正应力。
2、斜截面上的正应力和剪应力ατPαPPαA αp (a)(b)(c)图 2.9αp将斜截面上全应力分解成正应力和剪应力，有()⎪⎪⎩⎪⎪⎨⎧===+===).(αsin σαsin αcos σαsin τ.αcos σαcos σαcos σαααα4222132212100020p p ）（3、正负号规定-自x 轴逆时针转向斜截面外法线n ，为正；反之为负；-拉应力为正，压应力为负；-取保留截面内任一点为矩心，当对矩心顺时针转动时为正，反之为负4、最大应力和最小应力 1）当时，横截面，()AP==0σσmax α，2）当045±=α时，斜截面⎪⎪⎪⎩⎪⎪⎪⎨⎧===︒⨯===︒︒.σ-ττσsin στ)τ(σσ-minαmax αα045004502124522121）（3）当时，纵向截面，。
结论: 对于轴向拉（压）杆，()0σσmax α=发生在横截面上；()20/σmax α=τ发生在沿顺时针转45°角的斜截面上。
同样大小的剪应力也发生在的斜面上。
对于轴向受拉杆,可能沿横截面被拉断破坏,也可能沿450的斜截面被剪切而破坏。
5、一点处的应力状态因α,ατ,σαα有关与不同,对应的是不同方位的截面上的应力,过一点所作的各截面上的全部应力即称为该点的应力状态。
对轴向拉压杆 ， 0ααστσ可由、 (横截面上的正应力)完全确定,称为单向应力状态。
四、应力集中的概念图2.10 图2.11进一步的研究表明,对于轴向拉压的杆件,只有在离力的作用点较远处截面上的应力才是均匀分布的。
而且,在实际工程中 ,不少杆件截面尺寸会有突然的改变(如连接杆件上有哪钉孔的地方, 机械零件上有小缺 口、小孔、螺纹等的地方) 。
由于截面的突然改变,使得这些截面上的应力已不再是均匀分布,而是在孔口或缺口附近局部区域处急剧地增大,但稍稍离开这个区域后应力又趋于平均,如图2.10及图 2.11 所示。
