1-数轴上的距离公式与中点公式

初一动点问题的解题公式口诀
1、数轴上两点之间的距离。

可用绝对值来表示，即两点所表示的数差的绝对值。

如，数轴上点A，B所表示的数是a，b，则AB=|a-b|或｜b-a|。

2、数轴上一个动点用字母来表示。

用有理数的加法或减法即可解决，就是起点所表示的数加上或减去动点运动的距离，向正方向用加，负方向用减。

如，数轴上点A对应的数为－1，点P从A出发，以每秒2个单位长度的速度向右运动，设运动的时间是t，则点P所表示的数是－1+2t。

3、数轴上任意两点间的线段的中点。

两点所表示的数相加的和除以2，如数轴上的点所表示的数是a，b，则线段AB的中点所表示的数是（a+b)/2。

七上数学动点问题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（七上数学动点问题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为七上数学动点问题的全部内容。

动点问题（1）数轴上两点之间的距离公式：|a —b|(2）数轴上两点之间的中点公式：1。

已知A 、B 分别为数轴上两点，A 点对应的数是-20，B 点对应的数为100(1）求AB 中点M 对应的数；（2）若电子蚂蚁P 从B 出发，以6个单位/秒向左运动，电子蚂蚁Q 从A 出发，以4个单位/秒向左运动，电子蚂蚁R 从A 出发，以7个单位/秒向右运动。

当t 为多少的时候，蚂蚁R 恰好位于P 和Q 的中点？2。

如图,已知数轴上有三点A 、B 、C,AB=AC ，点C 对应的数是200（1）若BC=300，求A 点对应的数；（2）在（1）的条件下，动点P 、Q 分别从A 、C 两点同时出发向左运动，同时动点R 从A 点出发向右运动,当P 、Q 、R 的速度分别为每秒10单位长度、每秒5单位长度、每秒2单位长度，点M 为PR 中点，点N 为线段RQ 中点，多少秒恰好满足MR=4RN?3.已知数轴上两点A 、B 对应的数分别为-1、3，点P 为数轴上一动点。

当点P 以每分钟1个单位长度的速度从O 点向左运动时,点A 以每分钟5个单位长度向左运动，点B 以每分钟20个单位长度向左运动，若他们同时出发，那么多少分钟后P 点到点A 、点B 的距离相等？4。

如图，若点A 在数轴上对应的数为a ，点B 在数轴上对应的数为b ，且a 、b 满足：|a+2|+（b —1）2=0（1）求线段AB 的长；(2)若点P 是A 左侧的一点，PA 的中点为M ，PB 的中点为N ，当点P 在A 点左侧运动时，有两个结论： ①PM+PN 的值不变②PN—PM 的值不变其中只有一个结论正确，请判断正确结论,并求出其值.5。

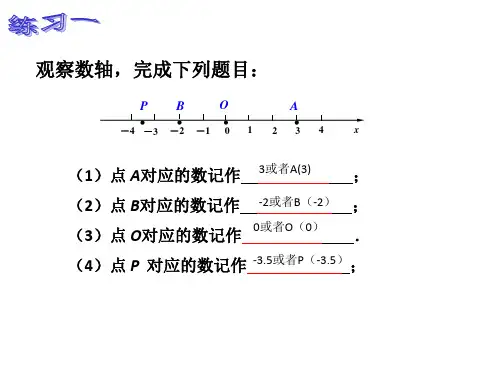
数轴上的距离公式与中点公式考点解析及例题讲解1. 数轴上点的坐标在数轴上，如果点P 与x 对应，则称点P 的坐标为x ，记作P (x )．练习一观察数轴，完成下列题目：（1）点P 与－3.5对应，则点P 的坐标是 ，记作 ；（2）点A 的坐标是 ，记作 ；（3）点B 的坐标是 ，记作 ；（4）点O 的坐标是 ，记作 ．2. 数轴上的距离公式探究一如图，填空：（1）图中点A 的坐标是 ，B 的坐标是 ，C 的坐标是 ，点D 的坐标是 ；（2）点A 与B 之间的距离|AB |=，点C 与A 之间的距离|CA |=，点B 与C 之间的距离|BC |=；（3）你能找出数轴上两点间距离与两个点坐标之间的关系吗？ 一般地，如果A (x 1)，B (x 2)，则这两点的距离公式为|AB |=|x 2－x 1|．探究二在以上例子中，我们遇到的数轴都是水平放置的，如果数轴不是水平放置的(如下图所示)，数轴上的距离公式成立吗？x ● xP ● ● ● B A O ● x● ● C ● ● 1 2 4 12 34B试求两个图中点A 与B 之间的距离．3. 数轴上的中点公式探究三根据下图回答问题：（1）点A (－1)，C (－3)的中点坐标是多少？中点坐标与A ，C 两点的坐标有怎样的关系？（2）点A (－1)，D (1)的中点坐标是多少？中点坐标与A ，D 两点的坐标有怎样的关系？一般地，在数轴上，A (x 1)，B (x 2)的中点坐标x 满足关系式x ＝ x 1＋x 22．4. 应用例 已知点A (－3)，B (5)，求：（1）|AB |；（2）A ，B 两点的中点坐标．解 （1）|AB |＝|5－(－3)|＝8；（2）设点M (x )是A ，B 两点的中点，则x ＝ －3＋52＝1．即A ，B 的中点坐标为1．平面直角坐标系中的距离公式和中点公式1. 距离公式探究一如图，设A (x 1，y 1)，B (x 2，y 2)．y 轴作垂线AA 1，AA 2和BB 1，BB 2，垂足分别为A 1，A 2，B 1，B 2，其中直线BB 1和AA 2相交于点C ．两点的距离公式|AB |＝(x 2－x 1)2＋(y 2－y 1)2．x● ● C A D ●探究二求两点之间的距离的计算步骤：S1 给两点的坐标赋值x 1＝？，y 1＝？，x 2＝？，y 2＝？S2 计算两个坐标的差，并赋值给另外两个变量，即d x ＝x 2－x 1，d y ＝y 2－y 1；S3 计算d ＝d 2x ＋d 2y ； S4 给出两点的距离d ．例1 已知A (2，－4)，B (－2，3)，求|AB |．解 因为x 1＝2，x 2＝－2，y 1＝－4，y 2＝3，所以dx ＝x 2－x 1＝－2－2＝－4，d y ＝y 2－y 1＝3－(－4)＝7．因此|AB |＝d 2x ＋d 2y ＝(－4)2＋72 ＝65．练习一求两点之间的距离：（1）A (6，2)，B (－2，5)；（2）C (2，－4)，D (7，2)．2. 中点公式探究三如图所示，若已知A (x 1，y 1)，B (x 2，y 2)，那么怎么求它们的对称中心的坐标？设M (x ，y )是A ，B 的对称中心，即线段AB 的中点．过A ，B ，M 分别向x 轴，y 轴作垂线，AA 1，AA 2，BB 1，BB 2，MM 1，MM 2，垂足分别是A 1，A 2，B 1，B 2，M 1，M 2．在平面直角坐标系内，两点A (x 1，y 1)，B (x 2，y 2)的中点M (x ，y )的坐标满足x ＝x 1+x 22，y ＝y 1+y 22．例2 求证：任意一点P (x ，y )与点P '(－x ，－y )关于坐标原点成中心对称． 证明 设P 与P '的对称中心为(x 0，y 0)，则x 0＝x +(－x )2＝0，y 0＝y +(－y )2＝0．所以坐标原点为P 与P ′的对称中心．练习二求下列各点关于坐标原点的对称点：A (2，3)，B (－3，5)，C (－2，－4)，D (3，－5)．例3 已知坐标平面内的任意一点P (a ，b )，分别求它关于x 轴的对称点P ′，关于y 轴的对称点P ′′的坐标．练习三求下列点关于x 轴和y 轴的对称点坐标：A (2，3)，B (－3，5)，C (－2，－4)，D (3，－5)．例4 已知平行四边形ABCD 的三个顶点A (－3，0)，B (2，－2)，C (5，2)，求顶点D 的坐标．解 因为平行四边形的两条对角线的中点相同，所以它们的坐标也相同．设点D 的坐标为(x ，y )，则⎩⎪⎨⎪⎧x +22＝－3+52＝1y －22＝0＋22＝1解得⎩⎪⎨⎪⎧x ＝0y ＝4所以顶点D 的坐标为(0，4)．。

数轴上两点间中点公式
（a+b）/2。

如果这两点的坐标分别为a和b，中点坐标是：（a+b）/2。

在数学中，可以用一条直线上的点表示数，这条直线叫做数轴，在数学中有着广泛的运用。

两根互相垂直且有同一原点的数轴可以构成平面直角坐标系；三根互相垂直且有同一原点的数轴可以构成空间直角坐标系，以确定物体的位置。

具体如下：
数轴上两点的中点公式
中点表示的数值：(a+b)/2
简单证明:如图，设A>B，P点是AB的中点对应的数是x。

则PB的距离是x-b；则PA的距离是a-x；根据P是中点所以PB=PA。

即x-b=a-x 解得x=(a+b)/2
当A<B时，也可以得到x=(a+b)/2；A=B时也成立。

所以无论a，b为何值这个中点公式都成立，非常方便(不用分情况讨论)。

我们还可以把它变形成：a + (b-a)/2
(a+b)/2=a/2 + b/2=a- a/2 + b/2=a + (b-a)/2
这个变形公式可以清晰的看出中点和A点（x与a）的关系。

还有其它一些变形，例如a+b=2x，a=2x-b等等也是经常用到。

平面直角坐标系(概念，距离公式，中点公式)今天我们学习平面直角坐标系相关的一些基础概念和平面直角坐标的特点，距离公式，中点公式等。

在平面内，两条互相垂直且有公共原点的数轴组成平面直角坐标系。

水平的数轴称为x轴或横轴，取向右为正方向。

竖直的数轴称为y轴或纵轴，取向上方向为正方向。

两坐标轴的交点为平面直角坐标系的原点。

有序数对：我们把(a，b)这种有顺序的两个数a与b组成的数对，叫做有序数对。

例如直角坐标系中有一点P，过点P作x轴，y轴的垂线，它在x轴对应的数是a，在y轴对应的数是b，那么(a，b)叫做点P的坐标。

利用平面直角坐标系，可以把组成几何图形的点和满足方程的每一组数联系起来，代数和几何合二为一。

象限(坐标轴上的点不属于任何象限)两条坐标轴把坐标平面分成四个部分(从右上部分开始逆时针方向分为1，2，3，4象限)右上方叫第一象限：x>0，y>0左上方叫第二象限：x<0，y>0左下方叫第三象限：x<0，y<0右下方叫第四象限：x>0，y<0横坐标轴上的点：(x，0)；纵坐标轴上的点：(0，y)。

距离问题：点(a，b)距x轴的距离为b的绝对值，距y轴的距离为a的绝对值。

坐标轴上两点间距离：点A(a1，0)与点B(a2，0)的距离AB为a1-a2的绝对值。

点A(0，b1)与点B(0，b2)的距离AB为b1-b2的绝对值。

根据勾股定理，可以计算出点(a，b)与原点的距离，以及任意两点(a，b)(c，d)间距离。

平行于坐标轴的直线平行于x轴(或横轴)的直线上的点的纵坐标相同；平行于y轴(或纵轴)的直线上的点的横坐标相同。

角平分线若点(x，y)在一、三象限角平分线上，则x=y。

若点(x，y)在二、四象限角平分线上，则x=-y。

与坐标轴、原点对称关于x轴对称的点的横坐标相同，纵坐标互为相反数。

关于y轴对称的点的纵坐标相同，横坐标互为相反数。

关于原点对称的点的横坐标、纵坐标都互为相反数。

数轴两点间中点公式在我们学习数学的旅程中，有一个小小的但非常实用的知识点，那就是数轴两点间中点公式。

这玩意儿看起来可能有点不起眼，但是在解决很多数学问题的时候，那可是大显身手啊！咱先来说说啥是数轴。

想象一下，有一条直直的线，上面标着好多数字，从负数一直到正数，就像一条数字的跑道。

而在这条跑道上的两个点，比如说点 A 和点 B，它们之间就存在着一个神奇的中点。

那这个中点咋算呢？公式就是：中点坐标等于两点坐标之和的一半。

比如说，点 A 的坐标是 x1，点 B 的坐标是 x2，那中点的坐标 M 就是（x1 + x2）/ 2 。

我记得有一次给学生们讲这个知识点的时候，有个小同学瞪着大眼睛一脸懵地问我：“老师，这有啥用啊？”我笑了笑，给他举了个例子。

假设我们要在一条笔直的公路上找一个中间的位置来建一个休息站，已知公路的起点坐标是 10 公里处，终点坐标是 50 公里处。

那这个休息站应该建在多少公里的地方呢？咱们用中点公式一算，（10 + 50）/2 = 30 公里，是不是一下子就找到答案啦！这个公式在很多实际问题中都能派上用场。

比如说，测量一段距离，要找中间点标记；或者在设计图纸上，确定两个关键点之间的中心位置。

再深入一点，咱们把这个公式拓展到平面直角坐标系中。

如果有两个点 A（x1, y1）和 B（x2, y2），那它们的中点坐标就是（(x1 + x2)/ 2，(y1 + y2)/ 2）。

这就像是在一个大地图上找两个地方的中心一样。

做数学题的时候，这个中点公式也能帮我们节省不少时间。

比如有些几何题，告诉你两个顶点的坐标，让你求中线的方程，这时候中点公式就能轻松搞定第一步，找到中点坐标。

在生活中，我们也经常会不自觉地用到这个概念。

就像分蛋糕，要把蛋糕平均分成两份，其实就是在找中点嘛！总之，数轴两点间中点公式虽然看起来简单，但是用处可大着呢！它就像是我们数学工具包里的一把小锤子，遇到问题的时候敲一敲，说不定就能打开解决问题的大门。