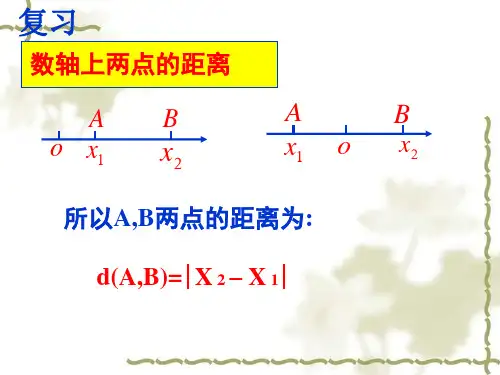
数轴上任意两点间的距离公式

数轴上两点间的距离公式好嘞，以下是为您生成的文章：在咱们学习数学的漫漫长路中，有一个小知识点就像一颗璀璨的星星，那就是数轴上两点间的距离公式。

这玩意儿听起来好像挺复杂，其实啊，搞懂了就会发现它超级简单又实用！我还记得有一次给学生们讲这个知识点的时候，有个小家伙瞪着大眼睛，一脸迷茫地问我：“老师，这数轴上的点跑来跑去的，距离咋算啊？”看着他那可爱又困惑的模样，我就知道得好好给他讲讲啦。

咱们先来说说数轴是啥。

想象一下，有一条直直的线，上面标着好多数字，从左到右越来越大，这就是数轴啦。

而数轴上的点呢，就像是一个个站在线上的小士兵，它们都有自己的位置。

那两点间的距离公式到底是啥呢？其实就是用右边点表示的数减去左边点表示的数。

比如说，数轴上有两个点，一个是 2，另一个是 5，那它们之间的距离就是 5 - 2 = 3。

咱们再举个例子，假如有两个点分别是 -3 和 1，那距离就是 1 - (-3) = 4 。

是不是挺简单的？但这还不够，咱们得知道为啥是这样算。

想象一下，你从一个点走到另一个点，走的路程不就是终点的位置减去起点的位置嘛。

而且这个距离公式在解决好多数学问题的时候都特别有用。

比如说，告诉你两个点的坐标，让你算它们的距离，这时候用上公式，一下子就能得出答案。

我之前碰到过一道题，说数轴上有 A、B 两点，A 点表示的数是 -5，B 点表示的数是 7，问 A、B 两点的距离是多少。

这时候，直接用距离公式 7 - (-5) = 12 ，答案就出来啦。

还有的时候，会反过来考你。

告诉你两点的距离和其中一个点的位置，让你求另一个点的位置。

这时候也别怕，根据距离公式慢慢推导就能算出来。

在实际生活中，这个距离公式也能派上用场呢。

比如说，你在地图上标记两个地点的位置，把地图想象成一个数轴，也能算出它们之间的“距离”。

总之啊，数轴上两点间的距离公式虽然看起来不起眼，但真的是数学世界里的一个好帮手。

只要咱们好好掌握它，就能在数学的海洋里畅游得更欢快！希望同学们以后遇到相关的问题，都能轻松搞定，加油哦！。

动点问题（1）数轴上两点之间的距离公式：|a-b|（2）数轴上两点之间的中点公式：1.已知A、B分别为数轴上两点，A点对应的数是-20，B点对应的数为100（1）求AB中点M对应的数；（2）若电子蚂蚁P从B出发，以6个单位/秒向左运动，电子蚂蚁Q从A出发，以4个单位/秒向左运动，电子蚂蚁R从A出发，以7个单位/秒向右运动。

当t为多少的时候，蚂蚁R恰好位于P和Q的中点？2.如图，已知数轴上有三点A、B、C，AB=AC，点C对应的数是200（1）若BC=300，求A点对应的数；（2）在（1）的条件下，动点P、Q分别从A、C两点同时出发向左运动，同时动点R从A 点出发向右运动，当P、Q、R的速度分别为每秒10单位长度、每秒5单位长度、每秒2单位长度，点M为PR中点，点N为线段RQ中点，多少秒恰好满足MR=4RN？A B C3.已知数轴上两点A、B对应的数分别为-1、3，点P为数轴上一动点。

当点P以每分钟1个单位长度的速度从O点向左运动时，点A以每分钟5个单位长度向左运动，点B以每分钟20个单位长度向左运动，若他们同时出发，那么多少分钟后P点到点A、点B的距离相等？4.如图，若点A在数轴上对应的数为a，点B在数轴上对应的数为b，且a、b满足：|a+2|+（b-1）2=0（1）求线段AB的长；（2）若点P是A左侧的一点，PA的中点为M，PB的中点为N，当点P在A点左侧运动时，有两个结论：①PM+PN的值不变②PN-PM的值不变其中只有一个结论正确，请判断正确结论，并求出其值。

5.已知数轴上三点M，O，N对应的数分别为-3，0, 1，点P为数轴上任意一点，其对应的数为x.（1）如果点P到点M，点N的距离相等，那么x的值是_____；（2）数轴上是否存在点P，使点P到点M，点N的距离之和是3？若存在，请直接写出x 的值；若不存在请说明理由；（3）如果点P以每分钟3个单位长度的速度从点O向左运动，点M和点N分别以每分钟1个单位长度和每分钟4个单位长度的速度也向左运动，且三点同时出发，那么几分钟时点P 到点M，点N的距离相等？6.如图，A、B两点在数轴上，点A表示的数为-10，OB=4OA，点M以每秒2个单位长度的速度从点A开始向左运动，点N以每秒3个单位长度的速度从点B开始向左运动（M、N 同时出发）（1）数轴上点B对应的数是____，线段AB中点C对应的数是______。

h f o一、与数轴上的动点问题相关的基本概念数轴上的动点问题离不开数轴上两点之间的距离。

主要涉及以下几个概念：1．数轴上两点间的距离，即为这两点所对应的坐标差的绝对值d=|a-b|也即用右边的数减去左边的数的差。

即数轴上两点间的距离=右边点表示的数—左边点表示的数。

两点中点公式：线段AB中点坐标=（a+b)÷22．点在数轴上运动时，由于数轴向右的方向为正方向，因此向右运动的速度看作正速度，而向作运动的速度看作负速度。

这样在起点的基础上加上点的运动路程就可以直接得到运动后点的坐标。

即一个点表示的数为a，向左运动b个单位后表示的数为a—b；向右运动b个单位后所表示的数为a+b。

3．数轴是数形结合的产物，分析数轴上点的运动要结合图形进行分析，点在数轴上运动形成的路径可看作数轴上线段的和差关系。

二、数轴上的动点问题基本解题思路和方法：1、表示出题目中动点运动后的坐标（一般用含有时间t的式子表示）。

2、根据两点间的距离公式表示出题目中相关线段长度（一般用含有时间t的式子表示）。

3、根据题目问题中线段的等量关系（一般是和、差关系）列绝对值方程。

4、解绝对值方程并根据实际问题验算结果。

（解绝对值方程通常用0点分类讨论方法）已知：b是最小的正整数，且a、b满足（c-5）2+|a+b|=0，请回答问题（1）请直接写出a、b、c的值．a=________，b=________，c=________（2）a、b、c所对应的点分别为A、B、C，点P为易动点，其对应的数为x，点P在0到2之间运动时（即0≤x≤2时），请化简式子：|x+1|-|x-1|+2|x+5|（3）（3）在（1）（2）的条件下，点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和p个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB．请问：BC-AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．r二、典例分析例1．已知数轴上有A、B、C三点，分别代表—24，—10，10，两只电子蚂蚁甲、乙分别从A、C两点同时相向而行，甲的速度为4个单位/秒。

动点问题万能公式是什么？
动点公式是(a+b)÷2，数轴上两点间的距离，即为这两点所对应的坐标差的绝对值，也即用右边的数减去左边的数的差，分析数轴上点的运动要结合图形进行分析。

点在数轴上运动时，由于数轴向右的方向为正方向，因此向右运动的速度看作正速度，而向作运动的速度看作负速度。

动点问题解题技巧：
1、数轴上两点间的距离，即为这两点所对应的坐标差的绝对值，也即用右边的数减去左边的数的差。

即数轴上两点间的距离=右边点表示的数-左边点表示的数。

2、点在数轴上运动时，由于数轴向右的方向为正方向，因此向右运动的速度看作正速度，而向作运动的速度看作负速度。

这样在起点的基础上加上点的运
动路程就可以直接得到运动后点的坐标。

即一个点表示的数为a，向左运动b 个单位后表示的数为a-b；向右运动b个单位后所表示的数为a+b。

3、数轴是数形结合的产物，分析数轴上点的运动要结合图形进行分析，点在数轴上运动形成的路径可看作数轴上线段的和差关系。

1．数轴（1）数轴的概念：规定了原点、正方向、单位长度的直线叫做数轴．数轴的三要素：原点，单位长度，正方向．（2）数轴上的点：所有的有理数都可以用数轴上的点表示，但数轴上的点不都表示有理数．（一般取右方向为正方向，数轴上的点对应任意实数，包括无理数．）（3）用数轴比较大小：一般来说，当数轴方向朝右时，右边的数总比左边的数大．✮（4）数轴上两点间的距离公式：AB=X B-X A (即：右端点减左端点）(即：中点等于两端点相加除以2）✮（5）数轴上中点数公式：X M=X A+X B2例题精讲【例1】.如图，点A在数轴上表示的数为﹣3，点B表示的数为2，点P在数轴上表示的是整数，点P不与A、B重合，且P A+PB＝5，则满足条件的P点表示的整数有___________.➢变式训练【变式1-1】．如图，点O为原点，A、B为数轴上两点，AB＝15，且OA＝2OB，点P从点B开始以每秒4个单位的速度向右运动，当点P开始运动时，点A、B分别以每秒5个单位和每秒2个单位的速度同时向右运动，设运动时间为t秒，若3AP+2OP﹣mBP的值在某段时间内不随着t的变化而变化，则m ＝．【变式1-2】．已知数轴上两点A、B对应的数分别是6，﹣8，M、N、P为数轴上三个动点，点M从A点出发，速度为每秒2个单位，点N从点B出发，速度为M点的3倍，点P从原点出发，速度为每秒1个单位．（1）若点M向右运动，同时点N向左运动，求多长时间点M与点N相距46个单位？（2）若点M、N、P同时都向右运动，求多长时间点P到点M，N的距离相等？（3）当时间t满足t1＜t≤t2时，M、N两点之间，N、P两点之间，M、P两点之间分别有47个、37个、10个整数点，请直接写出t1，t2的值．【例2】．如图，周长为6个单位长度的圆上的六等分点分别为A，B，C，D，E，F，点A落在2的位置，将圆在数轴上沿负方向滚动，那么落在数轴上﹣2023的点是．➢变式训练【变式2-1】．在数轴上，点A，O，B分别表示﹣15，0，9，点P，Q分别从点A，B同时开始沿数轴正方向运动，点P的速度是每秒4个单位，点Q的速度是每秒1个单位，运动时间为t秒．若点P，Q，O 三点在运动过程中，其中一个点恰好是另外两点为端点的线段的一个中点，则运动时间为秒．【变式2-2】．如图：在数轴上A点表示数﹣3，B点示数1，C点表示数9．（1）若将数轴折叠，使得A点与C点重合，则点B与数表示的点重合；（2）若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动．①若t秒钟过后，A，B，C三点中恰有一点为另外两点的中点，求t值；②当点C在B点右侧时，是否存在常数m，使mBC﹣2AB的值为定值，若存在，求m的值，若不存在，请说明理由．1．如图，将一刻度尺放在数轴上（数轴的单位长度是1cm），刻度尺上表示“0cm”“8cm”的刻度分别对应数轴上的是﹣3和x所表示的点，那么x等于（）A．5B．6C．7D．82．等边△ABC在数轴上的位置如图所示，点A、C对应的数分别为0和﹣1，若△ABC绕顶点沿顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1，则连续翻转2021次后，点B（）A．对应的数是2019B．对应的数是2020C．对应的数是2021D．不对应任何数3．在解决数学实际问题时，常常用到数形结合思想，比如：|x+1|的几何意义是数轴上表示数x的点与表示数﹣1的点的距离，|x﹣2|的几何意义是数轴上表示数x的点与表示数2的点的距离．结合以上知识，下列说法中正确的个数是（）①若|x﹣2022|＝1，则x＝2021或2023；②若|x﹣1|＝|x+3|，则x＝﹣1；③若x＞y，则|x﹣2|＞|y﹣2|；④关于x的方程|x+1|+|x﹣2|＝3有无数个解．A．1B．2C．3D．44．数轴上点A表示的数是﹣3，把点A向右移动5个单位，再向左移动7个单位到A′，则A′表示的数是．5．数轴上点A表示﹣8，点B表示6，点C表示12，点D表示18．如图，将数轴在原点O和点B，C处各折一下，得到一条“折线数轴”．在“折线数轴”上，动点M从点A出发，以4个单位/秒的速度沿着折线数轴的正方向运动，从点O运动到点C期间速度变为原来的一半，过点C后继续以原来的速度向终点D运动；点M从点A出发的同时，点N从点D出发，一直以3个单位/秒的速度沿着“折线数轴”负方向向终点A运动．其中一点到达终点时，两点都停止运动．设运动的时间为t秒，t时，M、N两点相遇（结果化为小数）．6．如图，在一条不完整的数轴上，从左到右的点A、B、C把数轴分成①②③④四部分，点A、B、C对应的数分别是a、b、c，且ab＜0．（1）原点在第部分（填序号）；（2）化简式子：|a﹣b|﹣|c﹣a|﹣|a|；（3）若|c﹣5|+（a+1）2＝0，且BC＝2AB，求点B表示的数．7．已知b是最小的正整数，且（c﹣5）2与|a+b|互为相反数．（1）填空：a＝，b＝，c＝；（2）若P为一动点，其对应的数为x，点P在0和2表示的点之间运动，即0≤x≤2时，化简：|x+1|﹣|x﹣1|+2|x+5|（请写出化简过程）；（3）如图，a，b，c在数轴上所对应的点分别为A，B，C，在（1）的条件下，若点A以1个单位长度/s的速度向左运动，同时，点B和点C分别以2个单位长度/s和5个单位长度/s的速度向右运动．ts后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB．请问：BC﹣AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．8．数轴上有A、B、C三点，如图1，点A、B表示的数分别为m、n（m＜n），点C在点B的右侧，AC﹣AB＝2．（1）若m＝﹣8，n＝2，点D是AC的中点．①则点D表示的数为﹣2．②如图2，线段EF＝a（E在F的左侧，a＞0），线段EF从A点出发，以1个单位每秒的速度向B点运动（点F不与B点重合），点M是EC的中点，N是BF的中点，在EF运动过程中，MN的长度始终为1，求a的值；（2）若n﹣m＞2，点D是AC的中点，若AD+3BD＝4，试求线段AB的长．9．如图，数轴上点A，B分别表示数a，b，其中a＜0，b＞0．（1）若a＝﹣7，b＝3，求线段AB的长度及线段AB的中点C表示的数c；（2）该数轴上有另一点D表示数d．①若d＝2，点D在点B的左侧，且AB＝5BD．求整式2a+8b+2023的值；②若d＝﹣2，且AB＝5BD，能否求整式2a+8b+2023的值？若能，求出该值；若不能，说明理由．10．先阅读，后探究相关的问题【阅读】|5﹣2|表示5与2差的绝对值，也可理解为5与2两数在数轴上所对应的两点之间的距离；|5+2|可以看做|5﹣（﹣2）|，表示5与﹣2的差的绝对值，也可理解为5与﹣2两数在数轴上所对应的两点之间的距离．（1）如图，先在数轴上画出表示点4.5的相反数的点B，再把点A向左移动1.5个单位，得到点C，则点B和点C表示的数分别为和，B，C两点间的距离是；（2）若点A表示的整数为x，则当x为﹣2时，|x+6|与|x﹣2|的值相等；（3）要使代数式|x+1|+|x﹣2|取最小值时，相应的x的取值范围是．11．如图，已知点O为数轴的原点，点A、B、C、D在数轴上，其中A、B两点对应的数分别为﹣1、3．（1）填空：线段AB的长度AB＝；（2）若点A是BC的中点，点D在点A的右侧，且OD＝AC，点P在线段CD上运动．问：该数轴上是否存在一条线段，当P点在这条线段上运动时，P A+PB的值随着点P的运动而没有发生变化？（3）若点P以1个单位/秒的速度从点O向右运动，同时点E从点A以5个单位/秒的速度向左运动、点F从点B以20个单位/秒的速度向右运动，M、N分点别是PE、OF的中点．点P、E、F的运动过程中，的值是否发生变化？请说明理由．12．如图，在数轴上，点O表示原点，点A表示的数为﹣1，对于数轴上任意一点P（不与点A点O重合），线段PO与线段P A的长度之比记作k（p），即，我们称k（p）为点P的特征值，例如：点P表示的数为1，因为PO＝1，P A＝2，所以．（1）当点P为AO的中点时，则k（p）＝；（2）若k（p）＝2，求点P表示的数；（3）若点P表示的数为p，且满足p＝2n﹣1，（其中n为正整数，且1≤n≤7），求所有满足条件的k（p）的和．13．把一根小木排放在数轴上，木棒左端点与点A重合，右端点与点B重合，数轴的单位长度为1cm，如图所示．（1）若将木棒沿数轴向右移动，当木棒的左端点移动到点B处时、它的右端点在数轴上对应的数为20；若将木棒沿数轴向左移动时，当它的右端点移动到点A处时，木棒左端点在数轴上对应的数为5，由此可得木棒的长为5cm；我们把这个模型记为“木捧摸型”；（2）在（1）的条件下，已知点C表示的数为﹣2．若木棒在移动过程中，当木棒的左端点与点C相距3cm时，求木棒的右端点与点A的距离；（3）请根据（1）的“木棒模型”解决下列问题．某一天，小字问爷爷的年龄，爷爷说：“我若是你现在那么大，你还要41年才出生；你若是我现在这么大，我就有124岁了，世界级老寿星了，哈哈！”请你画出“木棒模型”示意图，求出爷爷现在的年龄．14．对于数轴上的A，B，C三点，给出如下定义：若其中一个点与其它两个点的距离恰好满足2倍的数量关系，则称该点是其它两个点的“联盟点”．例如：数轴上点A，B，C所表示的数分别为1，3，4，此时点B是点A，C的“联盟点”．（1）若点A表示数﹣1，点B表示的数2，下列各数：，0，1，4，5所对应的点分别为C1，C2，C3，C4，C5，其中是点A，B的“联盟点”的是；（2）点A表示的数是﹣1，点B表示的数是3，P是数轴上的一个动点：①若点P在线段AB上，且点P是点A，B的“联盟点”，求此时点P表示的数；②若点P在点A的左侧，点P、A、B中有一个点恰好是其它两个点的“联盟点”，求出此时点P表示的数．15．如图，点A，O，B，D在同一条直线l上，点B在点A的右侧，AB＝6，OB＝2，点C是AB的中点，如图画数轴．（1）若点O是数轴的原点，则点B表示的数是，点C表示的数是；（2）若点O是数轴的原点时，D点表示的数为x，且AD＝5，求x；（3）若点D是数轴的原点，点D在点A的左侧，点A表示的数为m，且A，B，C，O所表示的数之和等于21，求m；（4）当O是数轴的原点，动点E，F分别从A，B出发，相向而行，点E的运动速度是每秒2个单位长度，点F的运动速度是每秒1个单位长度，当EF＝3时，求点A，B，E，F表示的数之和．16．如图，在数轴上点A表示数a，点B表示数b，点C表示数c，a，c满足|a+4|+（c﹣2）2＝0，b是最大的负整数．（1）a＝，b＝，c＝．（2）若将数轴折叠，使得点A与点C重合，则点B与数表示的点重合；（3）点A，B，C开始在数轴上运动，若点A和点B分别以每秒0.4个单位长度和0.3个单位长度的速度向左运动，同时点C以每秒0.2个单位长度的速度向左运动，点C到达原点后立即以原速度向右运动，运动时间为t秒，若点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，请问：5AB ﹣BC的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求出5AB﹣BC的值．17．定义：对于数轴上的三点，若其中一个点与其他两个点的距离恰好满足2倍的数量关系．如下图，数轴上点A，B，C所表示的数分别为1，3，4，此时点B就是点A，C的一个“关联点”．（1）写出点A，C的其他三个“关联点”所表示的数：、、．（2）若点M表示数﹣2，点N表示数4，数﹣8，﹣6，0，2，10所对应的点分别是C1，C2，C3，C4，C5，其中不是点M，N的“关联点”是点．（3）若点M表示的数是﹣3，点N表示的数是10，点P为数轴上的一个动点．①若点P在点N左侧，且点P是点M，N的“关联点”，求此时点P表示的数．②若点P在点N右侧，且点P，M，N中，有一个点恰好是另外两个点的“关联点”，求此时点P表示的数．18．[知识背景]：数轴上，点A，点B表示的数为a，b，则A，B两点的距离表示为AB＝|a﹣b|．线段AB 的中点P表示的数为．[知识运用]：已知数轴上A，B两点对应的数分别为a和b，且（a﹣4）2+|b﹣2|＝0，P为数轴上一动点，对应的数为x．（1）a＝，b＝；（2）若点P为线段AB的中点，则P点对应的数x为，若点B为线段AP的中点，则P点对应的数x为；（3）若点A、点B同时从图中位置在数轴上向左运动，点A的速度为每秒1个单位长度，点B的速度为每秒3个单位长度，则经过秒点B追上点A；（4）若点A、点B同时从图中位置在数轴上向左运动，它们的速度都为每秒1个单位长度，与此同时点P从表示﹣16的点处以每秒2个单位长度的速度在数轴上向右运动．经过多长时间后，点A、点B、点P 三点中，其中一点是另外两点组成的线段的中点？19．结合数轴与绝对值的知识回答下列问题：（1）探究：①数轴上表示5和3的两点之间的距离是．②数轴上表示﹣1和﹣4的两点之间的距离是．③数轴上表示﹣3和5的两点之间的距离是．（2）归纳：一般的，数轴上表示数a和数b的两点之间的距离等于．（3）应用：①若数轴上表示数a的点位于﹣4与3之间，则|a+4|+|a﹣3|的值＝．②若a表示数轴上的一个有理数，且|a﹣1|＝|a+3|，则a＝．③若a表示数轴上的一个有理数，|a﹣1|+|a+2|的最小值是．④若a表示数轴上的一个有理数，且|a+3|+|a﹣5|＞8，则有理数a的取值范围是．（4）拓展：已知，如图2，A、B分别为数轴上的两点，A点对应的数为﹣20，B点对应的数为100．若当电子蚂蚁P 从A点出发，以4个单位/秒的速度向右运动，同时另一只电子蚂蚁Q恰好从B点出发，以3单位/秒的速度向左运动，求经过多长时间两只电子蚂蚁在数轴上相距20个单位长度，并写出此时点P所表示的数．20．将一条数轴在原点O和点B处各折一下，得到如图所示的“折线数轴”，图中点A表示﹣10，点B表示10，点C表示18．我们称点A和点C在数轴上的“友好函数”为28个单位长度．动点P从点A出发，以2单位长度/秒的速度沿着“折线数轴”向其正方向运动．当运动到点O与点B之间时速度变为原来的一半．经过点B后立刻恢复原速；同时，动点Q从点C出发，以1单位长度/秒的速度沿着“折线数轴”向其负方向运动，当运动到点B与点O之间时速度变为原来的两倍，经过O后也立刻恢复原速．设运动的时间为t秒．（1）动点P从点A运动至点C需要秒，动点Q从点C运动至点A需要秒；（2）P，Q两点相遇时，求出相遇点M在“折线数轴”上所对应的数；（3）是否存在t值，使得点P和点Q任“折线数轴”上的“友好距离”等于点A和点B在“折线数轴”上的“友好距离”？若存在，求出t的值；若不存在，请说明理由．21．在数轴上，点M，N对应的数分别是m，n（m≠n，mn≠0），P为线段MN的中点，同时给出如下定义：如果＝10，那么称M是N的“努力点”．例如：m＝1，n＝，M是N的“努力点”．（1）若|m﹣10|+（n+90）2＝0则m＝，n＝；（2）在（1）的条件下，下列说法正确的是（填序号）；①M是P的“努力点”；②M是N的“努力点”③N是M的“努力点”；④N是P的“努力点”（3）若mn＜0，且P是M，N其中一点的“努力点”，求值？22．在数轴上，O为原点，点A，B对应的数分别是a，b（a≠b，ab≠0），M为线段AB的中点．给出如下定义：若OA÷OB＝4，则称A是B的“正比点”；若OA×OB＝4，则称A是B的“反比点”．例如a＝2，时，A是B的“正比点”；a＝2，b＝﹣2时，A是B的“反比点”．（1）若|a+2|+（b﹣4）2＝0，则M对应的数为，下列说法正确的是（填序号）．①A是M的“正比点”；②A是M的“反比点”；③B是M的“正比点”；④B是M的“反比点”；（2）若ab＞0，且M是A的“正比点”，求的值；（3）若ab＜0，且M既是A，B其中一点的“正比点”，又是另一点的“反比点”，直接写出的值．23．在数轴上，把原点记作点O，表示数1的点记作点A．对于数轴上任意一点P（不与点O，点A重合），将线段PO与线段P A的长度之比定义为点P的特征值，记作，即＝，例如：当点P是线段OA 的中点时，因为PO＝P A，所以＝1．（1）如图，点P1，P2，P3为数轴上三个点，点P1表示的数是﹣，点P2与P1关于原点对称．①＝；②比较，，的大小（用“＜”连接）；（2）数轴上的点M满足OM＝OA，求；（3）数轴上的点P表示有理数p，已知＜100且为整数，则所有满足条件的p的倒数之和为．24．阅读下列材料：我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离；即|x|＝|x﹣0|；这个结论可以推广为|x1﹣x2|表示在数轴上数x1，x2对应点之间的距离．绝对值的几何意义在解题中有着广泛的应用：例1：解方程|x|＝4．容易得出，在数轴上与原点距离为4的点对应的数为±4，即该方程的x＝±4；例2：解方程|x+1|+|x﹣2|＝5．由绝对值的几何意义可知，该方程表示求在数轴上与﹣1和2的距离之和为5的点对应的x的值．在数轴上，﹣1和2的距离为3，满足方程的x对应的点在2的右边或在﹣1的左边．若x对应的点在2的右边，如图1可以看出x＝3；同理，若x对应点在﹣1的左边，可得x＝﹣2．所以原方程的解是x＝3或x ＝﹣2．例3：解不等式|x﹣1|＞3．在数轴上找出|x﹣1|＝3的解，即到1的距离为3的点对应的数为﹣2，4，如图2，在﹣2的左边或在4的右边的x值就满足|x﹣1|＞3，所以|x﹣1|＞3的解为x＜﹣2或x＞4．参考阅读材料，解答下列问题：（1）方程|x+3|＝5的解为；（2）方程|x﹣2020|+|x+1|＝2023的解为；（3）若|x+4|+|x﹣3|≥11，求x的取值范围．。

七年级数学数轴上的动点问题数轴上的线段与动点问题一、与数轴上的动点问题相关的基本概念数轴上的动点问题离不开数轴上两点之间的距离.主要涉及以下几个概念：1．数轴上两点间的距离，即为这两点所对应的坐标差的绝对值d=|a-b|,也即用右边的数减去左边的数的差.即数轴上两点间的距离=右边点表示的数—左边点表示的数.2.两点中点公式：线段AB中点坐标=（a+b）÷2.3.点在数轴上运动时，由于数轴向右的方向为正方向，因此向右运动的速度看作正速度，而向左运动的速度看作负速度.这样在起点的基础上加上点的运动路程就可以直接得到运动后点的坐标.即一个点表示的数为a，向左运动b个单位后表示的数为a—b；向右运动b个单位后所表示的数为a+b.4.数轴是数形结合的产物，分析数轴上点的运动要结合图形进行分析，点在数轴上运动形成的路径可看作数轴上线段的和差关系.二、数轴不动点问题求解的基本思路和方法：1.标明题目中动点的坐标(一般用含时间t的公式表示)。

2.根据两点间的距离公式，表示问题中相关线段的长度(一般用含时间t的公式表示)。

3.根据题中线段的等价关系(一般是和差关系)列出绝对值方程。

4、解绝对值方程并根据实际问题验算结果.注：数轴上线段的动点问题方法类似1.已知数轴上点a和b对应的数是-2和4，p是数轴上的动点，对应的数是x.A B－2－1 0 1 2 3 4(1)若P为AB线段的三等分点，求P对应的数；（2）数轴上是否存在P，使P到A点、B点距离和为10，若存在，求出x；若不存在，说明理由.(3)如果a点、b点和p点(p点在原点)同时向左移动，它们的速度分别为1、2和1。

个长度单位/分，则第几分钟时，P为AB的中点？2、已知：b是最小的正整数，且a、b、c满足（c-5）2+|a+b|=0，请回答问题（1）请直接写出a、b、c的值．a=________，b=________，c=________（2）a、b、c所对应的点分别为A、B、C，点P为一动点，其对应的数为x，点P在到2之间运动时（即0≤x≤2时），请化简式子：|x+1|-|x-1|+2|x+5|.（3）若点A、点C分别以每秒1个单位和2个单位长度的速度向左运动，请问几秒时，A，C之间的距离为1个单位长度？(4)点a、b、c开始在数轴上移动。