导热微分方程

导热微分方程柱坐标系的推导引言导热微分方程是描述物质内部热传导过程的重要方程。

在研究导热现象时，我们常常需要在不同的坐标系下推导导热微分方程。

本文将详细介绍如何在柱坐标系下推导导热微分方程，并给出相应的推导过程。

导热微分方程的一般形式在三维空间中，导热微分方程的一般形式可以表示为：∂u/∂t = α(∂^2u/∂x^2 + ∂^2u/∂y^2 + ∂^2u/∂z^2)其中，u表示温度场的变化，t表示时间，x、y和z分别表示空间的三个坐标轴方向。

α为热扩散系数，与物质的热导率有关。

柱坐标系下的导热微分方程柱坐标系是一种常用的坐标系，特点是以距离r、角度θ和高度z作为坐标轴。

在柱坐标系下，可以将导热微分方程表示为：∂u/∂t = α(1/r * ∂/∂r(r∂u/∂r) + 1/r^2 * ∂^2u/∂θ^2 + ∂^2u/∂z^2)其中，r表示距离，θ表示角度，z表示高度，u仍表示温度场的变化，t为时间，α为热扩散系数。

推导过程为了推导柱坐标系下的导热微分方程，我们需要使用二阶导数的链式法则和柱坐标系下的坐标变换关系。

首先，我们分别对r、θ和z求偏导：∂u/∂r = (∂u/∂x) * (∂x/∂r) + (∂u/∂y) * (∂y/∂r) + (∂u/∂z) * (∂z/∂r)∂u/∂θ = (∂u/∂x) * (∂x/∂θ) + (∂u/∂y) * (∂y/∂θ) + (∂u/∂z) * (∂z/∂θ)∂u/∂z = (∂u/∂x) * (∂x/∂z) + (∂u/∂y) * (∂y/∂z) + (∂u/∂z) * (∂z/∂z)根据柱坐标系的坐标变换关系：x = r * cos(θ)y = r * sin(θ)z = z可以得到：∂x/∂r = cos(θ)∂y/∂r = sin(θ)∂z/∂r = 0∂x/∂θ = -r * sin(θ)∂y/∂θ = r * cos(θ)∂z/∂θ = 0∂x/∂z = 0∂y/∂z = 0∂z/∂z = 1代入前面的式子，可以得到：∂u/∂r = (∂u/∂x) * cos(θ) + (∂u/∂y) * sin(θ)∂u/∂θ = -r * sin(θ) * (∂u/∂x) + r * cos(θ) * (∂u/∂y)∂u/∂z = (∂u/∂z)然后，我们可以对这些偏导数再次求偏导：∂^2u/∂r^2 = (∂/∂r(∂u/∂r)) = (∂/∂r((∂u/∂x) * cos(θ) + (∂u/∂y) * sin (θ)))∂^2u/∂θ^2 = (∂/∂θ(∂u/∂θ)) = (∂/∂θ(-r * sin(θ) * (∂u/∂x) + r * cos(θ) * (∂u/∂y)))∂^2u/∂z^2 = (∂/∂z(∂u/∂z))最后，将这些结果代入柱坐标系下的导热微分方程的一般形式中，即可得到柱坐标系下的导热微分方程：∂u/∂t = α(1/r * (∂/∂r(r * ((∂u/∂x) * cos(θ) + (∂u/∂y) * sin(θ)))) + 1/r^2 * (∂/∂θ(-r * sin(θ) * (∂u/∂x) + r * cos(θ) * (∂u/∂y))) + (∂^2u/∂z ^2))总结导热微分方程是描述物质内部热传导过程的重要方程。

在直角坐标系中，导热微分方程是描述热量在空间中传播和分布的数学模型。

它是研究热传导过程中温度分布变化的重要工具，对于工程、物理学和生物学等领域都具有重要的应用价值。

导热微分方程的一般表达式是一个复杂但十分重要的数学问题，下面我将从简单到复杂，由浅入深地探讨这一主题。

我们需要了解什么是导热微分方程。

导热微分方程是描述物质内部温度分布随时间演变的方程，它是热传导方程的数学表达形式。

在直角坐标系中，导热微分方程可以用偏微分方程来表示。

通常情况下，导热微分方程可以写成如下形式：\[ \frac{\partial T}{\partial t} = k \left( \frac{\partial^2 T}{\partialx^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2T}{\partial z^2} \right) \]其中，\( T \) 代表温度，\( t \) 代表时间，\( x,y,z \) 分别代表空间直角坐标系中的坐标，\( k \) 是介质的热导率。

这个方程描述了温度随时间和空间坐标的变化规律，是具有深刻物理意义的方程。

接下来，我们可以进一步讨论这个方程的物理意义。

其中，\( \frac{\partial T}{\partial t} \) 表示温度随时间的变化率，\( \frac{\partial^2 T}{\partial x^2}, \frac{\partial^2 T}{\partialy^2}, \frac{\partial^2 T}{\partial z^2} \) 分别表示温度在 x、y、z方向上的曲率，而 \( k \) 则是介质的热导率。

这意味着方程右边的每一项都代表了热量在空间中传播时的一部分，它们的和则描述了整个空间内温度分布的变化。

在应用导热微分方程时，我们通常需要结合特定的边界条件和初值条件，才能够得到具体的温度分布。

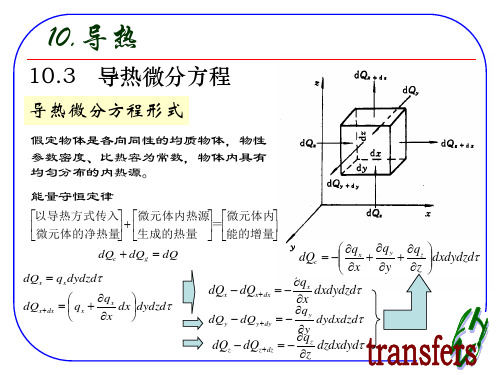
方程推导1.导热微分方程x 方向导入微元体的热流量为dydz xT x ∂∂-=λφ x+dx 方向导出微元体的热流量为： dx dydz xT x dx x x x x dx x )(∂∂-∂∂+=∂∂+=+λφφφφ 同理可得y 、z 方向的导入、导出热流量。

根据能量守恒：导入微元体的总热流量+微元体内的生成热=导出微元体的总热流量+微元体内能的增加 微元体内能的增加：dxdydz T cdU ∂τ∂ρ= 微元体内的生成热：dxdydz q ⋅ 经整理有：⋅+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=q z T z y T y x T x T c ∂∂λ∂∂∂∂λ∂∂∂∂λ∂∂∂τ∂ρ 该式可在（1）导热系数为常数；（2）导热系数为常数，无内热源（3）导热系数为常数、稳态（4）导热系数为常数、无内热源、稳态等情况下简化 圆柱坐标系：⋅+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=q z T z T r r T r r r T c ∂∂λ∂∂∂φ∂λ∂φ∂∂∂λ∂∂∂τ∂ρ211 球坐标系：⋅+⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=q T r T r r T r r r T c ∂φ∂λ∂φ∂θ∂θ∂θλ∂φ∂θ∂∂λ∂∂∂τ∂ρ22222sin 1sin sin 11 2.连续性方程 对于微平行六面体，从左边流入的质量为：τρρdydzd dx x u u dx x x x )2)(2(∂∂-∂∂-，从右边流出的质量为τρρdydzd dx x u u dx x x x )2)(2(∂∂+∂∂+，二者的净质量差为：τρdxdydzd x u x ∂∂-)( 同理可得y 、z 方向的质量变化，而经过d τ时间，微元体的质量变化为ττρdxdydzd ∂∂，因此可得平衡关系，经整理，有()()()0=∂∂+∂∂+∂∂+∂∂z w y v x u ρρρτρ，此方程可以在有关条件下简化。

导热微分方程是描述温度场满足的重要微分方程之一。

它在热传导、传热、能量传递等方面都有着重要的应用。

本文将从导热微分方程的定义、导出过程、物理意义和应用领域等方面进行介绍。

希望通过本文的阐述，读者能够对导热微分方程有一个更加全面深入的了解。

一、导热微分方程的定义导热微分方程是描述物体内部温度分布随时间变化的微分方程。

通常情况下，导热微分方程可以写成下面的形式：\[ \frac{\partial u}{\partial t} = k\Delta u \]其中，u代表温度场，t代表时间，k代表热传导系数，∆代表拉普拉斯算子。

这个方程描述的是温度场随时间t变化的规律，即温度场的时间变化率等于热传导系数和温度场的拉普拉斯算子的乘积。

二、导热微分方程的导出导热微分方程的导出过程涉及到热传导定律和能量守恒定律。

在导出过程中，我们首先根据热传导定律得到热传导方程，然后再利用能量守恒定律得到导热微分方程。

1. 热传导定律热传导定律是描述物体内部热量传递规律的定律，通常可以表示为：\[ q = -kA\frac{dT}{dx} \]其中，q代表热量传递速率，k代表热传导系数，A代表传热截面积，dT/dx表示温度梯度。

这个定律说明了热量会从高温区传递到低温区，热传导的速率与温度梯度成正比。

2. 能量守恒定律能量守恒定律说明了热能在空间中的传递与积累规律，它可以表示为：\[ \frac{\partial u}{\partial t} + \nabla \cdot q = 0 \]其中，u代表单位质量的内能，t代表时间，q代表单位面积上的热量通量。

这个定律说明了热能在空间中的传递与积累总是满足能量守恒的原则。

通过热传导定律和能量守恒定律的联立，可以得到导热微分方程的导出过程。

三、导热微分方程的物理意义导热微分方程描述了温度场随时间的变化规律，具有重要的物理意义。

它可以帮助我们理解物体内部温度分布随时间的演化情况，从而预测物体的温度变化趋势。