第九讲 植树问题

《植树问题》课件xx年xx月xx日•植树问题的概述•植树问题的基本公式•植树问题的求解方法•植树问题的应用案例目•植树问题的扩展知识录01植树问题的概述植树问题是一种经典的组合优化问题，涉及到在一条线段上放置若干个点（树），以及在每两个点之间连接一条线（树与树之间的连线），目标是使得所有点的连通性最好。

植树问题定义植树问题的复杂度较高，需要运用图论、组合优化等知识进行求解。

问题复杂度什么是植树问题1植树问题的分类23在一条线段上等距离放置若干个点，求最优连通性方案。

普通植树问题在一条线段上随机放置若干个点，其中部分点有障碍不能放置树，求最优连通性方案。

障碍植树问题在一条线段上放置若干个点，每个点可以分支为两个子点，求最优连通性方案。

分支植树问题03交通路网规划交通路网规划中需要考虑到道路连通性、交通流量等因素，可以运用植树问题的思想进行优化。

植树问题的应用场景01网络路由优化网络路由优化可以看作是在网络拓扑结构中求解最优连通性方案，与植树问题类似。

02城市绿化规划城市绿化规划中需要考虑到街道、公园等区域的绿化，可以运用植树问题的思想进行规划。

02植树问题的基本公式公式法根据线性植树问题的基本公式，求出每株树木之间的距离，用公式表示为：d = g / (n - 1)变量法用变量表示树木之间的距离，用n表示树木的数量，用d表示每株树木之间的距离，则线性植树问题的基本公式为：d = g / (n - 1)线性植树问题的基本公式公式法根据环形植树问题的基本公式，求出每株树木之间的距离，用公式表示为：d = g / n变量法用变量表示树木之间的距离，用n表示树木的数量，用d表示每株树木之间的距离，则环形植树问题的基本公式为：d = g / n环形植树问题的基本公式根据区域植树问题的基本公式，求出每个区域之间的距离，用公式表示为：d = g / (n - 1)公式法用变量表示区域之间的距离，用n表示区域的数量，用d表示每个区域之间的距离，则区域植树问题的基本公式为：d = g / (n - 1)变量法区域植树问题的基本公式03植树问题的求解方法根据植树问题的已知条件，列出关于距离、数量等变量的方程。

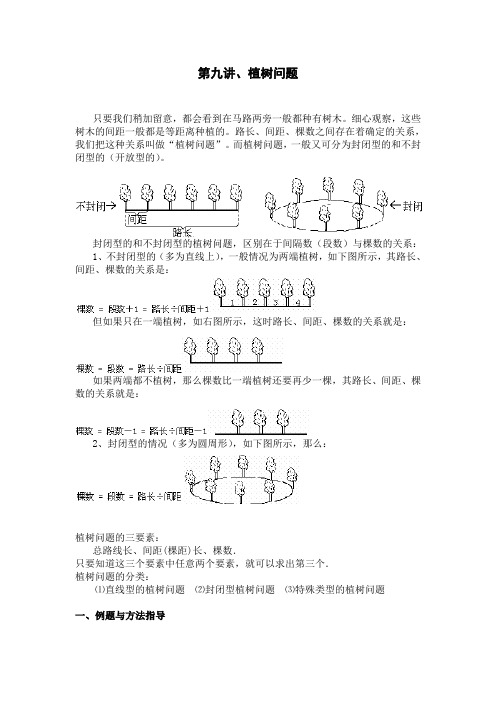
第九讲、植树问题只要我们稍加留意，都会看到在马路两旁一般都种有树木。

细心观察，这些树木的间距一般都是等距离种植的。

路长、间距、棵数之间存在着确定的关系，我们把这种关系叫做“植树问题”。

而植树问题，一般又可分为封闭型的和不封闭型的（开放型的）。

封闭型的和不封闭型的植树问题，区别在于间隔数（段数）与棵数的关系：1、不封闭型的（多为直线上），一般情况为两端植树，如下图所示，其路长、间距、棵数的关系是：但如果只在一端植树，如右图所示，这时路长、间距、棵数的关系就是：如果两端都不植树，那么棵数比一端植树还要再少一棵，其路长、间距、棵数的关系就是：2、封闭型的情况（多为圆周形），如下图所示，那么：植树问题的三要素：总路线长、间距(棵距)长、棵数．只要知道这三个要素中任意两个要素，就可以求出第三个．植树问题的分类：⑴直线型的植树问题⑵封闭型植树问题⑶特殊类型的植树问题一、例题与方法指导例1 有一条公路长1000米，在公路的一侧每隔5米栽一棵垂柳，可种植垂柳多少棵?思路导航：每隔5米栽一棵垂柳，即以两棵垂柳之间的距离5米为一段。

公路的全长1000米，分成5米一段，那么里包含有1000÷5=200段。

由于公路的两端都要求种树，所以要种植的棵数比分成的段数多1，所以，可种植垂柳200+1=201棵。

例2 某一淡水湖的周长1350米，在湖边每隔9米种柳树一株，在两株柳树中间种植2株夹枝桃，可栽柳树多少株?可栽夹枝桃多少株?两株夹枝桃之间相距多少米?思路导航：在圆周上植树时，由于可栽的株数等于分成的段数，所以，可栽柳树=1350÷9=150株；由于两株柳树之间等距离地栽株夹枝桃，而间隔数（段数）为150，所以栽夹枝桃的株数=2×150=300株；每隔9米种柳树一株，在两株夹枝桃之间等距地栽2株夹枝桃，这就变成两端都不植树的情形，即2株等距离栽在9米的直线上，不含两端，所以，每两株之间的距离=9÷(2+1)=3(米)。

81251000⨯=425100⨯= 小数乘除巧算一、【名师解析】1、乘法凑整运算性质。

思想核心：先把能凑成整十、整百、整千的几个乘数结合在一起，最后再与前面的数相乘，使得运算简便。

例如1025=⨯ 理论依据：乘法交换律：a ×b=b ×a乘法结合律：(a ×b) ×c=a ×(b ×c)乘法分配律：(a+b) ×c=a ×c+b ×c积不变规律：a ×b=(a ×c) ×(b ÷c)=(a ÷c) ×(b ×c)小数四则混合运算的运算顺序与整数四则混合运算的顺序相同。

整数的运算定律在小数运算中仍然适用。

2、小数乘、除法计算方法（1）小数乘法：计算小数乘法，先按照整数乘示的法则算出积，再看乘数中一共有几位小数，就从积的右边起数出几位，点上小数点。

乘数与积的位数关系：乘数中一共有几位小数，积中就有几位小数。

注意：①要数清楚两个乘数中小数的位数，弄清楚应补上几个0。

②确定积的小数点位置时，应先点上小数点，然后再把小数末尾的0划掉。

（2）小数除法：①除数是整数的小数除法：小数除法的意义与整数除法的意义相同，是已知两个乘数的积与其中的一个乘数，求另一个乘数的运算。

（被除数与商的小数点对齐）②整数除以整数，商是小数的小数除法的计算方法：先按照整数除法的法则去做，如果除到被除数的末尾仍有余数，就在后面填上0继续除。

③除数是小数：A.商不变的规律：被除数和除数同时扩大或缩小相同的倍数（0除外），商不变。

b.除数是小数的小数除法的计算方法：要把被除数和除数扩大相同的倍数，使除数变成整数，再按照小数除以整数的方法进行计算。

（3）把一个数的小数点向左（右）每移一位，这个数就缩小（扩大）10倍。

二、【例题精讲】例1.计算：0.125×0.25×0.5×64 80×25×2×1.25×0.5×0.4练习：计算（1）1.31×12.5×8×2 （2）1.25×32×0.25 （3）1.25×88（4）20×12.5×0.8×0.5 （5）64×12.5×0.25×0.05例 2.计算：（1）0.125÷（3.6÷80）×0.18 （2）47.85÷6.38×0.638（3）（0.6× 1.38）÷（13.8×4.8）（4）4.92÷0.25÷0.4练习：计算（1）36.363÷（1.2121×4）（2）36÷0.15÷0.12（3）7.68÷2.5÷0.4 （4）1.1÷（1.1÷1.2）÷（1.2÷1.3）÷（1.3÷1.4）例3.计算：（1）1.25×1.08 （2）7.5×9.9练习：计算（1）0.56×9.8 （2）2.5×10.4（3）3.8×0.99 （4）76.5×10.2 例4.计算：312.5×12.3－312.5×6.9＋312.5练习：计算（1）9.56×4.18－7.3×4.18－0.26×4.18（2）3.14×6.5+4.5×3.14-3.14例5.计算：（1）2000×199.9－1999×199.8（2）4.56×0.27＋483×0.0456＋1.9×4.56＋0.456×30练习：计算（1）200.9×20.08-200.8×20.07（2）1999×3.14+199.9×31.4+19.99×314例6.计算：1240×3.8+124×51+1.24×1400+760×9.6+0.76×700练习：计算15.6×78-15.6×14-64× 5.6 2.55⨯33.9+33.9⨯4.75+7.3⨯66.1【选讲】计算： 12.9÷0.72＋43.5÷3.6练习：计算： 117.8÷2.3－4.88÷0.23三、【综合精炼】一、计算下列各题：（1）8.376÷0.4÷2.5 （2）35÷0.125÷0.8（3）0.36÷[(6.1-4.6) 0.8] （4）（4.8×7.5×8.1）÷（2.4×2.5×2.7）（5）64×12.5×0.25×0.05 （6）8.7×10.1-0.87（7）47.5×99+47.5 （8）3.34×28.9+33.4×7.11（9）36×0.78+3.6×2.2 （10）17.48×37—174.8×1.9+1748×0.82 （11）199.9×19.98-199.8×19.97 （12）2.009×43+20.09×2.9+200.9×0.28二、计算下列各题：（1）3.75×4.8＋62.5×0.48 （2）20.09×31.5+2.009×317+200.9×3.68 （3）0.24 ×0.125÷0.3 （4）1250×0.037＋0.125×160＋12.5×2.7（5）16.46×15.1＋8.54×15.1－25×14.7 （6）75×4.67+5.99×25 （7）1.56×6.8+2.4×1.56+9.2×0.44 （8）6.3×27+1.9×21【挑战竞赛】 73÷3.6+105÷3.6+146÷3.6植树问题【名师解析】一、总路长、棵数、段数三者之间的关系：棵数×段数＝总路线长总路线长÷段数＝棵数总路线长÷棵数＝段数二、植树问题通常分为两类，封闭路线和不封闭路线：1．线段上的植树问题可以分为以下三种情形：（1）如果植树线路的两端都要植树，那么植树的棵数应比要分的段数多1，即：棵数=段数＋1；（2）如果一端植树，另一端不植树，那么棵数与段数相等，即：棵数=段数；（3）如果两端都不植树，那么棵数应比段数少1，即：棵数=段数－1。

植树问题的公式知识点：一、植树问题分两种情况，不封闭与封闭路线。

不封闭的植树路线.①若题目中要求在植树的线路两端都植树，则棵数比段数多1.全长、棵数、株距三者之间的关系是：棵数=段数1+=全长÷株距1+全长=株距⨯(棵数1-)株距=全长÷(棵数1-)②如果题目中要求在路线的一端植树，则棵数就比在两端植树时的棵数少1，即棵数与段数相等.全长、棵数、株距之间的关系就为：全长=株距⨯棵数；棵数=段数=全长÷株距；株距=全长÷棵数.③如果植树路线的两端都不植树，则棵数就比②中还少1棵.棵数=段数1-=全长÷株距1-.株距=全长÷(棵数1+).全长=株距⨯(棵数+1)封闭的植树路线.在圆、正方形、长方形、闭合曲线等上面植树，因为头尾两端重合在一起，所以种树的棵数等于分成的段数.棵数=段数=周长÷株距.二、解植树问题的三要素解决植树问题，首先要牢记三要素：总路线长、间距（棵距）长、棵数．只要知道这三个要素中任意两个要素，就可以求出第三个．三、方阵问题明确空心方阵和实心方阵的概念及区别.每边的个数＝总数÷41 ”；每向里一层每边棋子数减少2；掌握计算层数、每层个数、总个数的方法，及每层个数的变化规律。

板块一、非封闭的植树问题【例 1】大头儿子的学校旁边的一条路长400米，在路的一边从头到尾每隔4米种一棵树，一共能种几棵树？从图上可以看出，每隔4米种一棵树，如果20米长的路的一边共种了6棵树，这是因为我们首先要在这条路的一端种上一棵，就是说种树的棵树要比间距的个数多1，所以列式为：400÷4+1=101（棵）.【例 2】从小熊家到小猪家有一条小路，每隔45米种一棵树，加上两端共53棵；现在改成每隔60米种一棵树．求可余下多少棵树?【解析】该题含植树问题、相差关系两组数量关系.从小熊家到小猪家的距离是：45×(53-1)=2340(米)，间隔距离变化后，两地之间种树：2340÷60+1=40(棵)，所以可余下树： 53-40=13(棵) ，综合算式为：53-[45×(53-1)÷60+1]=13(棵).【例 3】马路的一边，相隔8米有一棵杨树，小强乘汽车从学校回家，从看到第一棵树到第153棵树共花了4分钟，小强从家到学校共坐了半小时的汽车，问：小强的家距离学校多远？【解析】第一棵树到第153棵树中间共有153-1=152（个）间隔，每个间隔长8米，所以第一棵树到第153棵树的距离是：152×8=1216（米），汽车经过1216米用了4分钟，1分钟汽车经过：1216÷4=304（米）,半小时汽车经过：304×30=9120（米），即小明的家距离学校9120米.【例 4】一位老爷爷以匀速散步，从家门口走到第11棵树用了11分钟，这位老爷爷如果走24分钟，应走到第几棵树？（家门口没有树）【解析】从家门口走到第11棵树是走了11个间隔，走一个间隔所用时间是：11÷11=1（分钟），那么走24分钟应该走了：24÷1=24（个）间隔，所以老爷爷应该走到了第24棵树.【例 5】晶晶上楼，从第一层走到第三层需要走36级台阶．如果从第一层走到第六层需要走多少级台阶?(各层楼之间的台阶数相同)【解析】题意的实质反映的是一线段上的点数与间隔数之间的关系．线段示意图如下：解：①每相邻两层楼之间有多少级台阶?÷-=(级)36(31)18②从第一层走到第六层共多少级台阶?⨯-=(级)18(61)90【例 6】元宵节到了，实验中学学校大门上挂了红绿两种颜色的彩灯，从头到尾一共挂了21只，每隔30分米挂一只红灯，相邻的2只红灯之间挂了一只绿灯，问实验中学学校的大门有多宽？【解析】一共挂了21只彩灯说明彩灯中间的间距有：21-1=20（个），每隔30分米挂一只红灯，相邻的2只红灯之间挂了一只绿灯，说明每个间距的长是：30÷2=15（分米），所以学而思学校的大门宽度为：15×20=300（分米）【例 7】有一个报时钟，每敲响一下，声音可持续3秒．如果敲响6下，那么从敲响第一下到最后一下持续声音结束，一共需要43秒．现在敲响12下，从敲响第一下到最后一下持续声音结束，一共需要多长时间？【解析】每次敲完以后，声音持续3秒，那么从敲完第一下到敲完第6下，一共经历的时间是43340-=（个）间隔，-=（秒），而这之间只有615所以每个间隔时间是4058÷=（秒），现在要敲响12下，所以一共经历的时间是11个间隔和3秒的持续时间，一共需要时间是：118391⨯+=（秒）．【例 8】小明家的小狗喝水时间很规律，每隔5分钟喝一次水，第一次喝水的时间是8点整，当小狗第20次喝水时，时间是多少？【解析】第20次喝水与第1次喝水之间有20119-=(个)间隔，因为小狗每隔5分钟喝一次，所以到第20次喝水中间间隔的时间是：19595⨯=(分钟)，也就是1个小时35分钟，所以小狗第20次喝水时时间是：9时35分．【例 9】裁缝有一段16米长的呢子，每天剪去2米，第几天剪去最后一段？【解析】如果呢子有2米，不需要剪；如果呢子有4米，第一天就可以剪去最后一段，4米里有2个2米，只用1天；如果呢子有6米，第一天剪去2米，还剩4米，第二天就可以剪去最后一段，6米里有3个2米，只用2天；如果呢子有8米，第一天剪去2米，还剩6米，第二天再剪2米，还剩4米，这样第三天即可剪去最后一段，8米里有4个2米，用3天，……我们可以从中发现规律：所用的天数比2米的个数少1．因此，只要看16米里有几个2米，问题就可以解决了．16米中包含2米的个数：1628÷=（个）剪去最后一段所用的天数：817-=（天），所以裁缝第7天剪去最后一段．【例 10】有一根180厘米长的绳子，从一端开始每3厘米作一记号，每4厘米也作一记号，然后将标有记号的地方剪断，绳子共被剪成了多少段？【解析】⑴每3厘米作一记号，共有记号：1803159÷-=（个）⑵每4厘米作一记号，共有记号：1804144÷-=（个）⑶其中重复的共有： 18012114÷-=（个）⑷所以记号共有：59441489+-=（个）⑸绳子共被剪成了： 89190+=（段）．【例 11】在一根长100厘米的木棍上，自左至右每隔6厘米染一个红色点，同时自右向左每隔5厘米也染一个红点，然后沿红点将木棍逐级锯开，那么长度是4厘米的短木棍有多少根？【解析】由于100是5的倍数，所以自右向左每隔5厘米染一个红点相当于自左向右每隔5厘米染一个红点．而每隔30厘米可得到2个4厘米的短木棍．最后10030310-⨯=（厘米）也可以得一个短木棍，故共有⨯+=（个）4厘米的短棍．2317【例 12】同学们做操，小林站在左起第5列，右起第3列；从前数前面有4个同学，从后数后面有6个同学．每行每列的人数同样多，做操的同学一共有多少人？【解析】带领学生画图求解．一共有几行？列式：4+6+1=11（行）一共有几列？列式：5317+-=（列）一共有多少人？列式：11777⨯=（人）【例 13】北京市国庆节参加游行的总人数有60000人，这些人平均分为25队，每队又以12人为一排列队前进．排与排之间的距离为1米，队与队之间的距离是4米，游行队伍全长多少米？【解析】这道题仍是植树问题的逆解题，它与植树问题中已知树的棵数，树间的距离，求树列的全长相当．逆解时要注意段数比树的棵数少1．所以，⑴每队的人数是：60000252400÷=(人)⑵每队可以分成的排数是：240012200÷=(排)⑶200排的全长米数是：1(2001)199⨯-=(米)⑷25个队的全长米数是：199254975⨯=(米)⑸25个队之间的距离总米数是：4(251)96⨯-=(米)⑹游行队伍的全长是：4975965071+=(米)【例 14】学而思学校三年级运动员参加校运动会入场式，组成66⨯的方块队(即每行每列都是6人)，前后每行间隔为2米．他们以每分钟40米的速度，通过长30米的主席台，需要多少分钟？【解析】通过下表理清解题思路．方块队通过主席台需要多少分钟？通过的路程总长÷方块队行进的速度(40米／分钟)方块队长+主席台长(30米)？运用植树问题的逆解思路，即前后每行间隔长×间隔数=方块队长．方块队长：2(61)10⨯-= (米)，方块队通过主席台行进路程总长：103040+=(米)，方块队通过主席台需要：40401÷=(分钟)，综合算式：[2(61)30]401⨯-+÷=(分钟)．【巩固】 1一条公路的一旁连两端在内共植树91棵，每两棵之间的距离是5米，求公路长是多少米？【解析】 根据植树问题得到：()9115450-⨯=（米）【巩固】 2从甲地到乙地每隔40米安装一根电线杆，加上两端共51根；现在改成每隔60米安装一根电线杆．求还需要多少根电线杆?【解析】 该题含植树问题、相差关系两组数量关系.解：①从甲地到乙地距离多少米?40(511)2000⨯-=(米)②间隔距离变化后，甲乙两地之间安装多少根电线杆?+=（根）200020100÷=(根)，1001101③还需要下多少根电线杆?-=(根)1015150综合算式：[40(511)201]5150⨯-÷+-=(根)【巩固】3马路的一边每相隔9米栽有一棵柳树.张军乘汽车5分钟共看到501棵树.问汽车每小时走多少千米？【解析】张军5分钟看到501棵树意味着在马路的两端都植树了；只要求出这段路的长度就容易求出汽车速度.解：5分钟汽车共走了：⨯-=(米)，9(5011)4500汽车每分钟走：45005900÷=(米)，汽车每小时走：=(千米)9006054000⨯=(米)54列综合式：⨯-÷⨯÷=(千米)9(5011)560100054【巩固】5丁丁和爸爸两个人比赛跑楼梯，从一层开始比赛，丁丁到四层时，爸爸到三层，如此算来，丁丁到16层时，爸爸跑到了几层？【解析】丁丁实际跑了三层的距离，爸爸跑了两层的距离，到16层需要跑15层的距离，所以丁丁跑了1535÷=（个）三层的距离，爸爸同时跑了5个两层的距离．所以爸爸跑到了52111⨯+=（层）．【巩固】7有一个挂钟，每小时敲一次钟，几点钟就敲几下，六点时，5秒钟敲完，那么十二点时，几秒钟才能敲完？【解析】六点时敲6下，中间共有5个间隔，所以每个时间间隔是551÷=（秒），十二点要敲12下，中间有11个时间间隔，所以十二点要用：11111⨯=（秒）才能敲完．【巩固】8科学家进行一项试验，每隔5小时做一次记录，做第12次记录时，挂钟时针恰好指向9，问做第一次记录时，时针指向几？【解析】我们先要弄清楚从第一次记录到第十二次记录中间经过的时间是多少．第1次到第12次有11个间隔：51155⨯=（小时）．然后我们要知道55小时，时针发生了怎样的变化．时针每过12小时就会转一圈回到原来的状态，所以时针转了4圈以后，又经过了7个小时．551247÷=L L（小时）而这时时针指向9点，所以原来时针指向2点．【巩固】9一根木料在24秒内被锯成了4段，用同样的速度锯成5段，需要多少秒？【解析】锯的次数总比锯的段数少1．因此，在24秒内锯了4段，实际只锯了3次，这样我们就可以求出锯一次所用的时间了，又由于用同样的速度锯成5段；实际上锯了4次，这样锯成5段所用的时间就可以求出来了．所以锯一次所用的时间：24(41)8÷-=（秒），锯5段所用的时间：⨯-=（）（秒）．85132【巩固】11一群小猴排成整齐的队伍做操，长颈鹿站在队伍旁边，一下子看到了他的好朋友金丝猴．长颈鹿数了数，金丝猴的左边有4只猴，右边也有4只猴，前面有5只猴，后面也有5只猴．小朋友，你能算出有多少只猴子在做操吗？【解析】一共有多少行？列式：5+5+1=11（行）【解析】一共有多少列？列式：4+4+1=9（列）【巩固】12一次检阅，接受检阅的一列彩车车队共30辆，每辆车长4米，前后每辆车相隔5米。

2019-2020学年度小学三年级数学奥数培优第九讲植树和年龄问题9.1植树问题[同步巩固演练]1、校园里有一段长80米的路，在路的一侧栽松树，第隔5米栽一棵，一共可以栽多少棵？2、“五一”节在一座桥的栏杆上插彩旗，从头到尾一共插了8面，第两面彩旗之间都相距8米，这座桥长多少米？3、一根木料截成3段要用10分钟，如果每截一段的时间相同，那么截成9段需要多长时间？4、学校教学楼从一层到四层共有45级台阶。

如果每层楼的台阶级数相等，那么从四层到十层一共有多少级台阶？5、马路上的每边相隔7米有一棵国槐，小军乘无轨电车3分看到马路的一边有国槐151棵，无轨电车每分钟行多少千米？6、一个花园周长200米，沿四周每隔5米栽一棵柳树，花园周围一共栽柳树多少棵？7、在正方形鱼塘四周种上树，四个顶点都种有一棵，这样每边都有22棵，四周共种多少棵？8、四年级三个班的同学在河堤上种了一排树，共80棵，从左往右数，第58棵起往右都是一班种的；从右往左数，第63棵起往左都是三班种的；那么三班种了多少棵？9、从新江到都市相距60千米，沿公路两旁植树，棵距20米，需树多少棵？若棵距15米，又需多少棵？10、一运动员参加马拉松赛跑，从看见第1个茶水站到看见第3个茶水站，共花了50分钟，已知从起点到终点每两个茶水站间隔为5千米，他跑完全长共花了3小时，问马拉松赛程是多少千米？11、某市计划在一条长30千米的马路上，由起点至终点每隔2千米设立一个车站，问不包括起点站与终点在这条马路上共有多少个车站？[能力拓展平台]1、一个木工锯一根长13米的木条，他先把一头损坏部分锯下1米，然后锯了5次，锯成许多一样长的短木条，求每根短木条长多少米？2、一个老人以等速在公路上散，从第一根电线杆走到第12根用了11分钟，这个老人如果走24分钟，应走到第几根电线杆？3、有一根长180厘米的绳子，从一端开始每3厘米作一记号，每4厘米也作一记号，然后将标有记号的地方剪断，绳子共被剪成多少段？4、在一个边长是60米的正方形池塘中间，沿对边中点修了两条堤坝（如图所示）。

植树问题知识点、重点、难点概念：以植树为内容,研究植树的棵树、棵与棵之间的距离(间隔数或棵距)和需要植树的总长度(总长)等数量间关系的问题,称为植树问题. 植树问题就是反应总长，间隔数和棵数这三个数量关系之间的关系。

植树问题在生活中很有实际运用价值,其基本数量关系和解题的要点是:1. 植树问题的基本数量关系:每段距离×段数=总距离.2. 在直线上植树要根据以下几种情况,弄清棵数与段数之间的关系:（1）在一段距离中,两端都植树,棵数=段数+1;(2)在一段距离中,两端都不植树,棵数=段数-1;(3)在一段距离中,一端不植树,棵数=段数.(4)在封闭曲线上植树,棵数=段数.第一种：一、先分析题意，再尝试解答:1、同学们在全长10 米的小路一边植树，每间隔5米栽一棵。

（两端要栽）一共要栽多少棵？间隔数是：树的棵树是：线段图：列式:2. 同学们在全长12 米的小路一边植树，每间隔3米栽一棵。

（两端要栽）一共要栽多少棵？间隔数是：树的棵树是：线段图：列式:3.同学们在全长20 米的小路一边植树，每间隔4米栽一棵（两端要栽）。

一共要栽多少棵？间隔数是：树的棵树是：线段图：列式:总结：棵数=段数（或间隔数）+1; 也就是：棵数=总长÷每段距离+1;二、根据数量关系式，列式解答：1、同学们在全长375米的小路一边植树，每间隔5 米栽一棵，（两端要栽）一共要栽多少棵？2、为了美化环境，学校准备在操场边上的一条100米长的小路一边植树，每隔5米栽一棵（两端要栽），需要准备多少棵树苗呢？3、有一条长1000米的公路,在公路的一侧从头到尾每隔25米栽一棵树苗,一共需要准备多少棵树苗?4、公路的一旁每隔40米有木电杆一根(两端都有).共121根.这条公路全长为多少米？第二种：一、先分析题意，再尝试解答:1、同学们在全长10 米的小路一边植树，每间隔5米栽一棵。

（两端不栽）一共要栽多少棵？间隔数是：树的棵树是：线段图：列式:2、同学们在全长10 米的小路一边植树，每间隔2米栽一棵。