《自动控制原理》第二版课后习题答案

自动控制原理第二版课后答案孟华【篇一：自动控制原理_孟华_习题答案】t>第二章2.1 试分别写出图2.68中各无源电路的输入ur(t)与输出uc(t)之间的微分方程。

图2.68 习题2.1图解：(a)ur?ucu?r?u?c)?i2，i1?i2?c?i1，c(ur1r2，r1r2rrr2?c?uc?12cu?r?cuurr1?r2r1?r2r1?r2(b)?r?u?c)?i1，c1(uur?u1?1，uc?i1r2?u1， ?i2，i1?i2?c2ur1??c?(r1c1?r1c2?r2c1)u?c?uc?r1r2c1c2u??r?(r1c1?r2c1)u?r?u r r1r2c1c2u(c)uur?uc?i1，c1(ur?u1)?i2，i1?i2?1r1r2，uc?1i1dt?u1， ?c2??c?(rc????r1r2c1c2u12?r2c2?r2c1)uc?uc?r1r2c1c2ur?(r2c2?r2c1)ur?ur2.2 试证明图2.69(a)所示电路与图2.69(b)所示的机械系统具有相同的微分方程。

图2.69(b)中xr(t)为输入，xc(t)为输出，均是位移量。

(a)(b)图2.69 习题2.2图(a)1ur?uc?r?u?c)?i2，i1?i2?i，uc??i1，c1(uidt?ir2，r1c2???c?(r1c1?r1c2?r2c2)u?c?uc?r1r2c1c2u??r?(r1c1?r2c2)u?r?u r r1r2c1c2u(b)?c?x?1)?k2x1，b1(x?r?x?c)?k1(xr?xc)?b2(x?c?x?1)， b2(xb1b2bbbbbbb??c?(1?2?2)x?c?xc?12??r?(1?2)x?r?xrxxk1k2k1k2k1k1k2k1k22.3 试分别求出图2.70中各有源电路的输入ur(t)与输出uc(t)之间的微分方程。

(a) (b)(c)图2.70 习题2.3图解：(a)uur?r??c?cur1r2，uc?r???r2cur2ur r1(b)uurr?c，r2cu?c?uc??2ur ??c?cur1r2r1uc??ur1u?c??r2cu?r?ur r2??rdt，r1cur1cr1(c)2.4 某弹簧的力-位移特性曲线如图2.71所示。

自动控制原理第二版课后答案1. 什么是自动控制原理？自动控制原理是一门研究如何设计、分析和实现自动控制系统的学科。

它涉及到信号处理、系统建模、控制算法设计等多个领域，是现代工程技术中的重要组成部分。

自动控制系统广泛应用于工业生产、交通运输、航空航天等领域，对提高生产效率、降低能耗、改善产品质量等方面起到了重要作用。

2. 为什么需要学习自动控制原理？学习自动控制原理可以帮助我们理解和掌握如何设计和优化控制系统，从而更好地解决实际工程问题。

掌握自动控制原理知识可以提高工程师的工作效率，同时也为未来的科研和创新打下坚实的基础。

3. 自动控制原理的基本概念。

自动控制系统由输入、输出、控制器和被控对象组成。

输入是系统的控制信号，输出是系统的反馈信号，控制器根据输入信号和输出信号进行计算，然后控制被控对象的行为。

自动控制系统的目标是使系统的输出信号尽可能接近期望值，从而实现对系统的精确控制。

4. 自动控制原理的数学模型。

自动控制系统可以用数学模型来描述，常见的数学模型包括微分方程、差分方程、状态空间方程等。

通过建立系统的数学模型，可以对系统进行分析和设计，从而实现对系统的控制。

5. 自动控制原理的控制算法。

控制算法是自动控制系统的核心部分，常见的控制算法包括比例控制、积分控制、微分控制、模糊控制、神经网络控制等。

不同的控制算法适用于不同的系统，可以根据实际情况选择合适的控制算法来实现对系统的控制。

6. 自动控制原理的应用。

自动控制原理在工业生产、交通运输、航空航天等领域有着广泛的应用。

例如，在工业生产中，自动控制系统可以实现对生产过程的精确控制，提高生产效率和产品质量；在交通运输领域，自动控制系统可以实现对交通信号、车辆行驶等方面的控制，提高交通运输效率和安全性。

7. 自动控制原理的发展趋势。

随着科学技术的不断发展，自动控制原理也在不断地发展和完善。

未来，自动控制系统将更加智能化、自适应化，能够更好地适应复杂多变的环境，实现对系统的更加精确和高效的控制。

自动控制原理及其应用第二版课后答案【篇一：《自动控制原理》黄坚课后习题答案】ss=txt>uo-u+o(a)解：i1=i-i2u1=ui-uouuu-ui=i1==211dud(u-u)i2=c=c(b)解：(u-u)i=i1+i2i=udui1=i2=c2duu1-uo=21u-uud(u-u)-c=12dudur2(ui-uo )=r1u0-cr1r2(-)duducr1r2+r1uo+r2u0=cr1r2+r2uidud2uuuduu--21112=2+cud2udu+(c+=12+(1+2)uo12duu+c2duo+22-2 求下列函数的拉氏变换。

(1) f(t)=sin4t+cos4t(2) f(t)=t3+e4t434t解：l[t+e](3) f(t)=tneat解：l[tneat]=(4) f(t)=(t-1)2e2t解：l[(t-1)2e2t]=e-(s-2)2-3求下列函数的拉氏反变换。

(1) f(s)=aa解：a1=(s+2)=-1a2=2 -f(t)=2e-3t-e-2t(2) f(s)=aaa解：a1=(s+1)=-1a2[=2a3s=-2=-2f(t)=-2e-2t-te-t+2e-t(3) f(s)=2as+aa解：f(s)(s2=a1s+a2j=a1s+aj-2-5j+1=ja1+a2-5j-1=-a1+ja2a1=1a2=-5a3=f(s)s=1++f(t)=1+cost-5sint(4) f(s)=解：=a+a+a+aa1a3a4a2ad[2]s=-1f(t)=e-t-e-t++e-3t(2-4)求解下列微分方程。

a2=5 a3=-4y(t)=1+5e-2t-4e-3t并求传递函数。

2-5试画题图所示电路的动态结构图，c+sc)r2r+rrscu(s)==c1+(+sc)r212121(2)cl1=-r2 /lsl2=-/lcs2l3=-1/scr1l1l3=r2/lcr1s2c112122-8 设有一个初始条件为零的系统，系统的输入、输出曲线如图，求g(s)。

自动控制原理_胡寿松_第二版_答案全解第二章控制系统数学模型练习及参考答案自动控制原理胡守松第二版课后解答2-2由牛顿第二运动定律，不管重力如何，都可以得到组织上述公式的拉普拉斯变换是通过注意运动从静止开始，即初始条件都为零而获得的所以传递函数是(2)取上弹簧和阻尼器之间的辅助点a，将点a的位移设定为x，方向向下；在作品的下半部分。

导出点作为辅助点B。

根据弹簧力和阻尼力平衡的原则，从点A和点B可分别列出下列原始方程:通过消除中间变量x，可以得到系统的微分方程。

对上述公式进行拉普拉斯变换，并考虑零的初始条件，系统传递函数为(3)以引出点为辅助点，根据力平衡原理，可列出以下原始方程:按项移位排序的系统微分方程对上述公式进行拉普拉斯变换，注意运动从静止开始，即那么系统传递函数是2-3(b)取k1和f1之间的辅助点A，设定点A的位移为X，方向向下；根据力平衡原理，可以列出以下原始方程:因此2-6解决方案:2-7解决方案:2-8解决方案:2-9解决方案:2-10解决方案:系统结构图如下:系统的传递函数是:2-11解决方案:(a)(b)(c)(d)(e)(f)2-12解决方案:第三章线性系统的时域分析练习和参考答案3-1解决方案:3-2溶液:3-3溶液:3-4解决方案:3-5解决方案:3-6解决方案:3-7解决方案:3-8解决方案:3-9解决方案:勒鲁斯的表格如下: 系统不稳定性3-10解决方案:(略) 3-11解决方案:系统的特征方程为: 简化；勒鲁斯的表格如下:。

自动控制原理孟华第二版课后答案【篇一：自动控制原理_孟华_习题答案大连理工】t>第一章（略）第二章2.1 试分别写出图2.68中各无源电路的输入ur(t)与输出uc(t)之间的微分方程。

图2.68 习题2.1图解：(a)ur?ucurrrrr2?c?uc?12cu?r??r?u?c)?i2，i1?i2?c，12cu?i1，c(uurr1r2r1?r2r1?r2r1?r2(b)?r?u?c)?i1，c1(uur?u1?1，uc?i1r2?u1， ?i2，i1?i2?c2ur1??c?(r1c1?r1c2?r2c1)u?c?uc?r1r2c1c2u??r?(r1c1?r2c1)u?r?u r r1r2c1c2u(c)u1ur?uc?i1，c1(ur?u1)?i2，i1?i2?1，uc?i1dt?u1， r1r2c2???c?(rc????r1r2c1c2u12?r2c2?r2c1)uc?uc?r1r2c1c2ur?(r2c2?r2c1)ur?ur2.2 试证明图2.69(a)所示电路与图2.69(b)所示的机械系统具有相同的微分方程。

图2.69(b)中xr(t)为输入，xc(t)为输出，均是位移量。

(a)(b)图2.69 习题2.2图解：(a)1ur?uc?r?u?c)?i2，i1?i2?i，uc??i1，c1(uidt?ir2，r1c2???c?(r1c1?r1c2?r2c2)u?c?uc?r1r2c1c2u??r?(r1c1?r2c2)u?r?u r r1r2c1c2u(b)?c?x?1)?k2x1，b1(x?r?x?c)?k1(xr?xc)?b2(x?c?x?1)， b2(x b1b2bbbbbbb??c?(1?2?2)x?c?xc?12??r?(1?2)x?r?xrxxk1k2k1k2k1k1k2k1k22.3 试分别求出图2.70中各有源电路的输入ur(t)与输出uc(t)之间的微分方程。

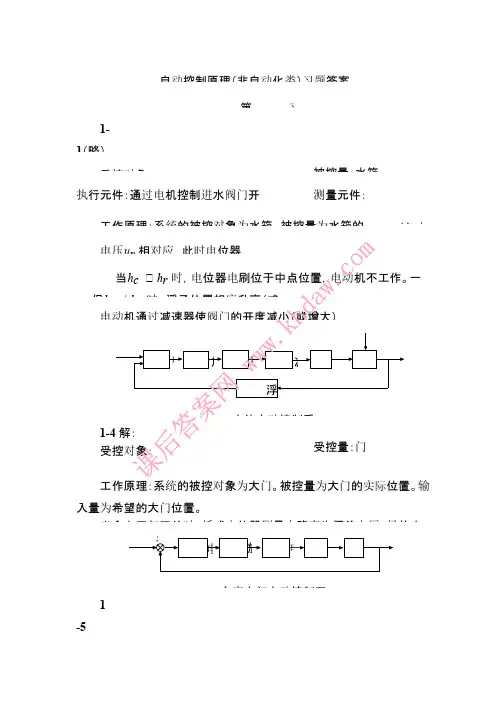
自动控制原理（非自动化类）习题答案第一章习题1-1（略）1-2（略）1-3解：受控对象：水箱液面。

被控量：水箱的实际水位h c 执行元件：通过电机控制进水阀门开度，控制进水流量。

比较计算元件：电位器。

测量元件：浮子，杠杆。

放大元件：放大器。

工作原理：系统的被控对象为水箱。

被控量为水箱的实际水位h 。

给定值为希望水位h （与电位器设定c r 电压u r 相对应，此时电位器电刷位于中点位置）。

当h c =h r 时，电位器电刷位于中点位置，电动机不工作。

一但h c ≠h r 时，浮子位置相应升高（或电动机通过减速器使阀门的开度减小（或增大），以使水箱水位达到希望值h r 。

出水h rh c水位自动控制系统的职能方框图1-4解：受控对象：门。

执行元件：电动机，绞盘。

放大元件：放大器。

受控量：门的位置测量比较元件：电位计工作原理：系统的被控对象为大门。

被控量为大门的实际位置。

输入量为希望的大门位置。

当合上开门开关时，桥式电位器测量电路产生偏差电压，经放大器放大后，驱动电动机带动绞盘转动，使大门向上提起。

同时，与大门连在一起的电位器电刷上移，直到桥式电位器达到平衡，电动机停转，开门开关自动断开。

反之，当合上关门开关时，电动机带动绞盘反转，使大门关闭。

开(闭)门的位置门实际仓库大门自动控制开（闭）的职能方框图1-5解：系统的输出量：电炉炉温给定输入量：加热器电压被控对象：电炉_大门位置绞盘电动机放大器电位器_浮子杠杆水箱阀门减速器电动机放大器电位器放大元件：电压放大器，功率放大器，减速器比较元件：电位计测量元件：热电偶职能方框图：给定炉温炉温—第二章习题2-1解：对微分方程做拉氏变换：⎧X 1(s )=R (s )−C (s )+N 1(s )⎪⎪X 2(s )=K 1X 1(s )⎪X 3(s )=X 2(s )−X 5(s )⎨⎪TsX 4(s )=X 3(s )⎪X 5(s )=X 4(s )−K 2N 2(s )⎪⎪K X (s )=s 2C (s )+sC (s )⎩35绘制上式各子方程的方块图如下图所示：N 1(s)R(s)+X 1(s)X 2(s)X 3(s)X 1(s)X 2(s)--C(s)X 5(s)N 2(s)X 3(s)X 4(s)X 5(s)C(s)X 4(s)-X 5(s)将方块图连接起来，得出系统的动态结构图：N 2(s)N 1(s)+X 1(s)_C(s)R(s)X 2(s)X 3(s)X 4(s)X 5(s)K 1K 3C (s )/R (s )=，Ts 3+(T +1)s 2+s +K K 13--K 3K 11s 2+s1TsK 2K 31Ts1s 2+sK 2K 1热电偶电炉加热器电机功率放大电压放大电位器C (s )/N 1(s )=C (s )/R (s )，K 2K 3TsC (s )/N (s )=−2Ts 3+(T +1)s 2+s +K K 132-2解：对微分方程做拉氏变换⎧X 1(s )=K [R (s )−C (s )]⎪⎪X 2(s )=⎜sR (s )⎪(s +1)X 3(s )=X 1(s )+X 2(s )⎨⎪(Ts +1)X 4(s )=X 3(s )+X5(s )⎪C (s )=X (s )−N (s )4⎪⎪⎩X 5(s )=(Ts +1)N (s )绘制上式各子方程的方块如下图：X 2(s)R(s)X 1(s)R(s)X 2(s)X 1(s)X 3(s)-C(s)X 5(s)N(s)N(s)X 5(s)—X 3(s)X 4(s)X 4(s)C(s)将方块图连接得出系统的动态结构图：N(s)X 2(s)X 5(s)—C(s)R(s)X 1(s)X 3(s)X 4(s)⎜s K+K +⎜s =(s +1)(Ts +1)(s +1)(Ts +1)=C (s )R (s )k Ts 2+(T +1)s +(K +1)1+(s +1)(Ts +1)C (s )N (s )=02-3解：（过程略）C (s )1C (s )=G 1+G 2(a)=R (s )ms 2+fs +K(b)R (s )1+G G −G G +G G −G G 13142324-K1Ts +11s +1τsTs+1Ts1Ts +1τsK1s +1C (s )=G 2+G 1G 2C (s )=G 1−G 2(c)(d)R (s )1+G 1+G 2G 1R (s )1−G 2G 3C (s )=G 1G 2G 3G 4(e)R (s )1+G 1G 2+G 2G 3+G 3G 4+G 1G 2G 3G 42-4解：（1）求C/R ，令N=0G (s )=K 1K 2K 3s (Ts +1)K 1K 2K 3G (s )C (s )/R (s )==1+G (s )Ts 2+s +K K K 123求C/N ，令R=0，向后移动单位反馈的比较点K 3K 2)Ts +1=K n K 3s −K 1K 2K 3G n C (s )/N (s )=(K −G K n n 1K K Ts 2+s +K K K s 1+32K 1231Ts +1s（2）要消除干扰对系统的影响C (s )/N (s )=K n K 3s −K 1K 2K 3G n=0Ts 2+s +K K K 123K n s G (s )=n K 1K 22-5解：（a ）（1）系统的反馈回路有三个，所以有3∑La=L 1+L 2+L 3=−G 1G 2G 5−G 2G 3G 4+G 4G 2G 5a =1三个回路两两接触，可得⊗=1−∑La=1+G 1G 2G 5+G 2G 3G 4−G 4G 2G 5（2）有两条前向通道，且与两条回路均有接触，所以P 1=G 1G 2G 3,⊗1=1P 2=1,⊗2=1（3）闭环传递函数C/R 为C =G 1G 2G 3+1R 1+G 1G 2G 5+G 2G 3G 4−G 4G 2G 5（b ）（1）系统的反馈回路有三个，所以有3∑La=L 1+L 2+L 3=−G 1G 2−G 1−G 1a =1三个回路均接触，可得⊗=1−∑L a=1+G 1G 2+（2）有四条前向通道，且与三条回路均有接触，所以P 1=G 1G 2,⊗1=1P 2=G 1,⊗2=1P 3=G 2,⊗3=1P 4=−G 1,⊗4=1（3）闭环传递函数C/R 为C =G 1G 2+G 1+G 2−G 1=G 1G 2+G 2R 1+G 1G 2+2G 11+G 1G 2+2G 12-6解：用梅逊公式求，有两个回路，且接触，可得⊗=1−∑La=1+G 1G 2G 3+G 2，可得C (s )=G 1G 2G 3+G 2G 3C (s )=C (s )/R (s )R (s )1+G 1G 2G 3+G 2N 1(s )(1+G 2)G 3C (s )=−1⋅(1+G 1G 2G 3+G 2)=−1C (s )=N 2(s )1+G 1G 2G 3+G 21+G 1G 2G 3+G 2N 3(s )E (s )=1+G 2−G 2G 3E (s )=−C (s )=−G 2G 3−G 1G 2G 3R (s )1+G 1G 2G 3+G 2N 1(s )N 1(s )1+G 1G 2G 3+G 2E (s )=−C (s )−(1+G 2)G 3E (s )=−C (s )==1N 2(s )N 2(s )1+G 1G 2G 3+G 2N 3(s )N 3(s )第三章习题103-1解：（原书改为G (s )=）0.2s +1采用K 0,K H 负反馈方法的闭环传递函数为10K 0⎫(s )=C (s )=K G (s )1+10K H =R (s )01+G (s )K 0.2s +1H1+10K H要使过渡时间减小到原来的0.1倍，要保证总的放大系数不变，则：（原放大系数为10，时间常数为0.2）10K 0⎧=10⎧K =10⎪0⎨1+10K ⇒⎨H⎩K =0.9⎪H 1+10K =10⎩H3-2解：系统为欠阻尼二阶系统（书上改为“单位负反馈……”，“已知系统开环传递函数”）⎛%=e −⎩/1−⎩⋅100%=1.3−1⋅100%21t p ==0.11−⎩2⎤n解得：⎤=33.71n⎩=0.358所以，开环传递函数为：113647.1G(s)==s(s+24.1)s(0.041s+1) 3-3解：（1）K=10s−1时：100G(s)=s2+10s⎤2=100n2⎩⎤=10n解得：⎤n=10,⎩=0.5,⎛%=16.3%,t p=0.363（2）K=20s−1时：200G(s)=s2+10s⎤2=200n2⎩⎤=10n解得：⎤n=14.14,⎩=0.354,⎛%=30%,t p=0.238结论，K增大，超调增加，峰值时间减小。

第二章控制系统的数学模型习题及参考答案自动控制原理胡寿松第二版课后答案2-2 由牛顿第二运动定律，在不计重力时，可得整理得将上式拉氏变换，并注意到运动由静止开始，即初始条件全部为零，可得于是传递函数为②其上半部弹簧与阻尼器之间，取辅助点A，并设A点位移为x，方向朝下；而在其下半部工。

引出点处取为辅助点B。

则由弹簧力与阻尼力平衡的原则，从A和B两点可以分别列出如下原始方程：消去中间变量x，可得系统微分方程对上式取拉氏变换，并计及初始条件为零，得系统传递函数为③以引出点作为辅助点，根据力的平衡原则，可列出如下原始方程：移项整理得系统微分方程对上式进行拉氏变换，并注意到运动由静止开始，即则系统传递函数为2-3(b)以k1和f1之间取辅助点A，并设A点位移为x，方向朝下；根据力的平衡原则，可列出如下原始方程：所以2-6解：2-7 解：2-8 解：2-9解：2-10 解：系统的结构图如下：系统的传递函数为：2-11 解：(a)(b)(c)(d)(e)(f)2-12 解：第三章线性系统的时域分析习题及参考答案自动控制原理胡寿松第二版课后答案3-1解：3-2 解：3-3 解：3-4 解：3-5 解：3-6 解：3-7 解：3-8 解：3-9 解：列劳斯表如下：系统不稳定3-10 解：（略）3-11 解：系统的特征方程为：化简得;列劳斯表如下：0<k<1.73-12 解：系统的开环传递函数为：特征方程为：列劳斯表如下：所以τ>03-13 解：（1）、（2）（3）3-14 解：（1）（2）（3）3-15 解：（1）系统的开环传递函数为：而（2）系统的开环传递函数为：而（3）系统的开环传递函数为：而同时作用下的系统误差为：第四章线性系统的根轨迹法习题及参考答案自动控制原理胡寿松第二版课后答案4-1 解：系统的开环传递函数为根轨迹如图所示4-2 解：4-3 解：（1）系统的开环传递函数为概略的根轨迹如下图所示：（2）系统的开环传递函数为根轨迹如下图所示4-4 解：（1）系统的开环传递函数为（2）系统的开环传递函数为有三个极点一个零点：（-20，j0）。

第一章习题参考答案B1.1分析比较开环控制系统,闭环控制系统的优缺点及其应用场合,并指出下列系统中哪些属于开环控制系统,哪些属于闭环控制系统?①家用空调机-------------------------------------------闭环②家用洗衣机-------------------------------------------开环③抽水马桶----------------------------------------------闭环④电饭煲-------------------------------------------------闭环⑤高楼水箱----------------------------------------------闭环⑥调光台灯----------------------------------------------开环⑦自动报时电子钟-------------------------------------开环⑧普通车床----------------------------------------------开环⑨母子钟系统-------------------------------------------开环B1.2 图B1.2为热水电加热器示意图，它向用户提供热水并向水箱补充冷水。

为了保持热水的期望温度，由温控开关接通或断开电加热器的电源。

试说明系统的工作原理并绘制其方块图。

期望温度实际温度温控开关电加热器水箱-测温元件B1.7 下列各式是描述系统的微分方程，其中ｙ(t)为输出量，u(t)为输入量。

试判断各系统属于何种类型(线性系统或非线性系统，定常系统或时变系统)，并说明其理由。

统。

（6）为非线性定常系。

（7）为线性时变系统（4）（5）（2）常系统。

（1）（3）为线性定线性增量系统。