自动控制原理C作业第二章答案

格式：doc
大小：1.05 MB
文档页数：20

下载文档原格式

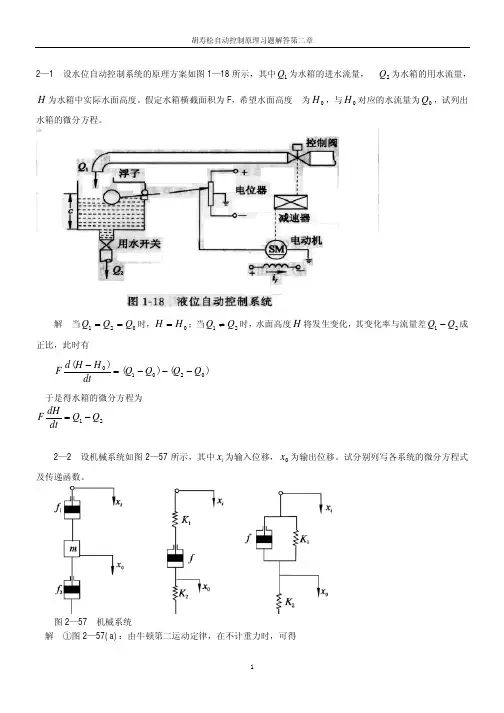
自动控制原理胡寿松主编课后习题答案详解-胡寿松第六版自控答案

6 dc(t) + 10c(t) = 20e(t) dt
20 db(t) + 5b(t) = 10c(t) dt
且初始条件均为零，试求传递函数 C(s) / R(s) 及 E(s) / R(s)
解：系统结构图及微分方程得：
G(s) = 20
H (s) = 10
6s + 10
20s + 5
20
C(s) = 10G(s) =
方程。解：
设正常工作点为 A，这时 Q0 = K P0
在该点附近用泰勒级数展开近似为：
y
=
f
(
x0
)
+
df (x) dx
x0
(
x
−
x0
)
即 Q − Q0 = K1 (P − P0 )
其中 K1
= dQ dP P=P0
=
1K 2
1 P0
2-7 设弹簧特性由下式描述：
F = 12.65 y1.1
2-3 试证明图2-58(ａ)的电网络与(b)的机械系统有相同的数学模型。
2
胡寿松自动控制原理习题解答第二章
图 2-58 电网络与机械系统
1
解：（a）：利用运算阻抗法得： Z1
=
R1
//
1 C1s
=
R1 C1s
R1
+
1 C1s
=
R1 = R1 R1C1s + 1 T1s + 1
Z2=Βιβλιοθήκη R2+1 C2s
运动模态 e −0.5t
−1t
所以： x(t) = t − 2(1 − e 2 )
(２) &x&(t) + x&(t) + x(t) = δ (t）。

自动控制原理-第2章习题解答精选全文完整版

第2章控制系统的数学模型习题及解答2-1 已知质量-弹簧系统如题2-1图所示，图中标明了质量和弹簧的弹性系数。

当外力F (t )作用时，系统产生运动，如果在不计摩擦的情况下，以质量m 2的位移y (t )为输出，外力F (t )为输入，试列写系统的运动方程。

解：设质量m 1的位移量为x (t ),根据牛顿第二定律有y k y x k dt yd m 21222-)(−= ①)(1221y x k F dtxd m −−= ②①式可以写作y k k x k dtyd m )(211222+−= ③由①式也可以得到y k dtyd m y x k 22221)(+=− ④③式两端同时求二阶导数，可得2221221442)(dty d k k dt x d k dt yd m +−= ⑤将②、③式代入⑤式中，整理可得F m k y m k k dty d m k m k m m dt y d m 1112122122121442)(=−++++ 2-2 求题2-2图中由质量-弹簧-阻尼器组成的机械系统，建立系统的运动方程。

其中，x (t )为基底相对于惯性空间的位移，y (t )为质量相对于惯性空间的位移。

z (t )= y (t )- x (t )为基底和质量之间的相对位移，z (t )由记录得到， x (t )和z (t )分别为输入量和输出量。

解：应用牛顿第二定律可得dtt dz f kz dt y d m )(22−−= 将z (t )= y (t )- x (t )代入上式，整理可得2222dtx d m kz dt dz f dt z d m −=++题2-2图题2-1图解：（a ）引入中间变量u c (t)表示电容器两端的电压。

根据基尔霍夫电流定律有o c c u R u R dt du C2111=+ 根据基尔霍夫电压定律有o i c u u u −=联立消去中间变量，可得描述输入量u i (t )和输出量u o (t )之间关系的微分方程为i i o o u R dt du C u R R R R dt du C121211+=++ （b ）引入回路电流i (t )和电容器两端的电压u c (t)作为中间变量，根据基尔霍夫电压定律有i o u u i R =+1 另有电容元件的元件约束关系方程dtdu Ci c =和i R u u o c 2−=联立求解，消去中间变量可得i i o o u R dt du C u R R R R dt du C121211+=++（c ）设电容器C 2两端的电压为u c 2(t)，根据基尔霍夫电流定律有dtduC u u R dt u u d C c o i o i 2211)(1)(=−+− ①求导可得22221221)(1)(dtu d C dt u u d R dt u u d C c o i o i =−+− ② 另有输出支路电压方程o c c u u dtdu C R =+2222 等式两边求导有dtdu dt du dt u d C R oc c =+222222 ③将①、②代入③式，整理可得i ii ooo u C R dt du C R C R C R dt u d C R u C R dt du C R C R C R C R dt u d C R 2121221121221212122112121122+++=++++2-4 试求题2-4图所示有源RC 电路的微分方程，其中u i (t )为输入量，u o (t )为输出量。

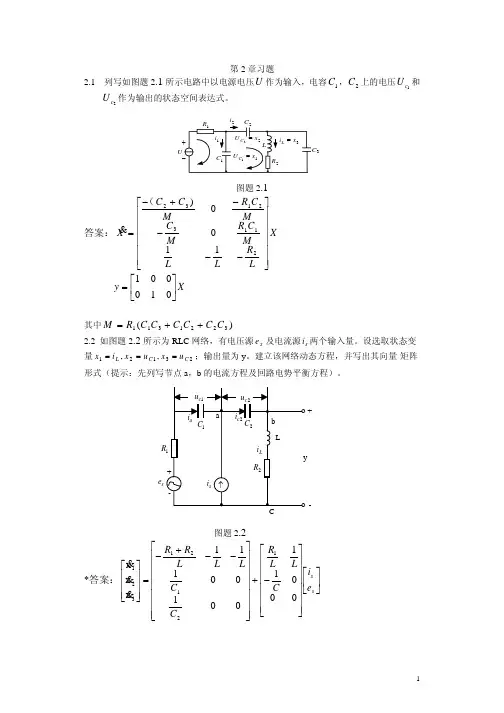
自动控制原理_王万良(课后答案2

第2章习题2.1 列写如图题2.1所示电路中以电源电压U 作为输入，电容1C ，2C 上的电压1c U 和2c U 作为输出的状态空间表达式。

图题2.1答案：X L R LL M C R M C M C R M C C X ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−−−−+−=211321321100)（& X y ⎥⎦⎤⎢⎣⎡=010001其中)(3221311C C C C C C R M ++=2.2 如图题2.2所示为RLC 网络，有电压源s e 及电流源s i 两个输入量。

设选取状态变量23121,,C C L u x u x i x ===；输出量为y 。

建立该网络动态方程，并写出其向量-矩阵形式（提示：先列写节点a ，b 的电流方程及回路电势平衡方程）。

图题2.2*答案：⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−+⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡−−+−=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡s s e i C L L R C C L L L RR 0001100100111x x x 12121321&&&U 3+-se[]111−−−=R y ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321x x x +[]⎥⎦⎤⎢⎣⎡s s e i R 11 2.3 列写图题2.3所示RLC 网络的微分方程。

其中，r u 为输入变量，c u 为输出变量图题2.3答案：r c cc u u dt du RC dtu d LC =++22 2.4 列写图题2.4所示RLC 网络的微分方程，其中r u 为输入变量，c u 为输出变量。

图题2.4答案：r c cc uu dt du R L dtu d LC =++22 2.5 图题2.5所示为一弹簧—质量—阻尼器系统，列写外力)(t F 与质量块位移)(t y 之间)(t图题2.5答案：)()()()(22t f t ky dt t dy f dtt y d m =++ 2.6 列写图题2.6所示电路的微分方程，并确定系统的传递函数，其中r u 为输入变量,cu 为输出变量。

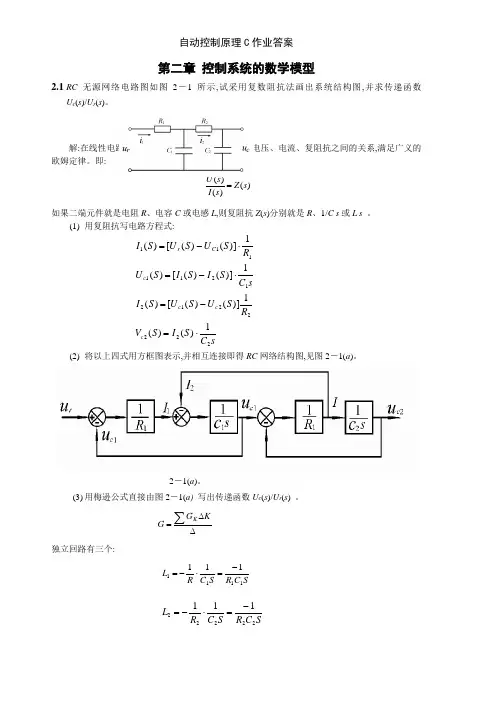
自动控制原理C作业答案

第二章控制系统的数学模型2.1RC无源网络电路图如图2－1所示,试采用复数阻抗法画出系统结构图,并求传递函数U c(s)/U r(s)。

图2－1解:在线性电路的计算中,引入了复阻抗的概念,则电压、电流、复阻抗之间的关系,满足广义的欧姆定律。

即:)()()(sZsIsU=如果二端元件就是电阻R、电容C或电感L,则复阻抗Z(s)分别就是R、1/C s或L s。

(1)用复阻抗写电路方程式:sCSISVRSUSUSIsCSISISURSUSUSIccccCr222221212111111)()(1)]()([)(1)]()([)(1)]()([)(⋅=-=⋅-=⋅-=(2)将以上四式用方框图表示,并相互连接即得RC网络结构图,见图2－1(a)。

2－1(a)。

(3)用梅逊公式直接由图2－1(a)写出传递函数U c(s)/U r(s) 。

∆∆=∑KGG K独立回路有三个:SCRSCRL1111111-=⋅-=SCRSCRL22222111-=⋅-=回路相互不接触的情况只有L 1与L 2两个回路。

则2221121121S C R C R L L L == 由上式可写出特征式为:222111222112132111111)(1S C R C R S C R S C R S C R L L L L L ++++=+++-=∆通向前路只有一条221212*********SC C R R S C R S C R G =⋅⋅⋅=由于G 1与所有回路L 1,L 2, L 3都有公共支路,属于相互有接触,则余子式为Δ1=1代入梅逊公式得传递函数1)(111111121221122121222111222112221111++++=++++=∆∆=s C R C R C R s C C R R s C R C R s C R s C R s C R s C R C R G G 2-2 已知系统结构图如图2-2所示,试用化简法求传递函数C (s )/R (s )。

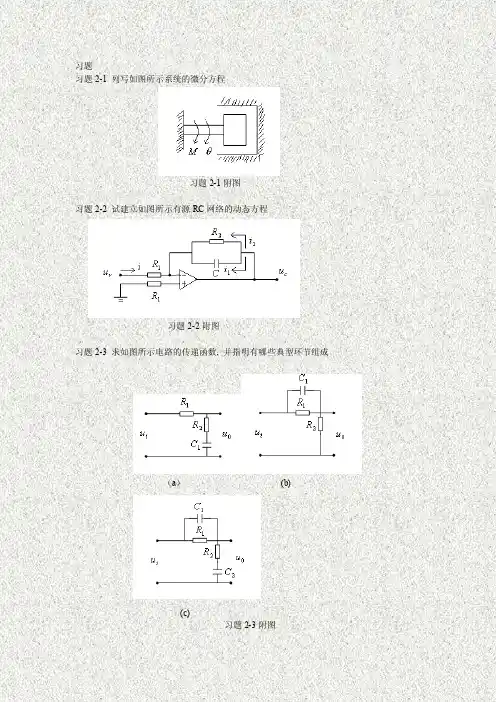
自动控制原理第二章习题答案详解

习题习题2-1 列写如图所示系统的微分方程习题2-1附图习题2-2 试建立如图所示有源RC网络的动态方程习题2-2附图习题2-3 求如图所示电路的传递函数, 并指明有哪些典型环节组成（a）(b)(c)习题2-3附图习题2-4 简化如图所示方块图, 并求出系统传递函数习题2-4附图习题2-5 绘制如下方块图的等效信号流图, 并求传递函数图（a）图(b)习题2-5附图习题2-6 系统微分方程组如下, 试建立对应信号流图, 并求传递函数。

),(d )(d )(),(d )(d ),()()()(),()(),(d )(d )(),()()(54435553422311121t y tt y T t x k t x k tt x t y k t x t x t x t x k t x t x k tt x t x t y t r t x +==--==+=-=τ习题2-7 利用梅逊公式直接求传递函数。

习题2-7附图习题2-8 求如图所示闭环传递函数, 并求(b)中)(s H x 的表达式, 使其与(a)等效。

图（a ）图（b）习题2-8附图习题2-9 求如下各图的传递函数（a）(b)(c)习题2-9附图习题2-10 已知某些系统信号流图如图所示, 求对应方块图（a ）(b)(c)(d)习题2-10附图习题答案习题2-1答案：解:设外加转矩M 为输入量,转角θ为输出量,转动惯量J 代表惯性负载,根据牛顿定律可得:θθθ1122d d d d k t f M tJ --=式中,1,1,k f 分别为粘性阻尼系数和扭转弹性系数,整理得:M k t f tJ =++θθθ1122d d d d习题2-2答案：解: 设r u 为输入量,c u 为输出量,,,,21i i i 为中间变量,根据运算放大器原理可得:1221d d R u i R u i t u c i r c c ===消去中间变量可得: r c c u R Ru t u C R 122d d -=+ 习题2-3答案：解: (a)11111111221212211121121120++=+++=+++=+++=Ts Ts s R R R C R s C R R sC R sC R sC sC R R sC R u u i β其中:221121,R R R C R T +==β, 一阶微分环节，惯性环节.(b)21121212111221122011//1R R s C R R R s C R R R sC R R R sC R R u u i+++=++=+= 11111111212121221121111++=+∙++∙+=+++=Ts Ts s C R R R R s C R R R R R R s C R R s C R αα其中 α=+=21211,R R R T C R , 一阶微分环节，惯性环节.(c)s C R s C R s C R s C R s C R sC R R sC sC R u u i 21221122112211220)1)(1()1)(1(1//11+++++=+++= 由微分环节，二阶振荡环节组成。

《自动控制原理》---丁红主编---第二章习题答案

2－1（1）a.微分方程（2）a.线性定常2-2.方框、信号线、综合点、引出点2-3.变换变量关系保持不变。

2-4. 222222121)(nn n s s s T s T s G ωζωωζ++=++= 2-5. 输入信号)t (r 和输出信号)t (c 及其各阶导数在0t =时的值均为零。

2-6解：取分离体分析受力如图3－1－3所示。

依据牛顿定律可得()()()22)(dt t y d m a m t f t f t f K B =⋅=-- (1) 式中 K f ── 弹簧力；()t f B ── 阻尼力。

弹簧力与物体位移成正比，即)(t y K f K ⋅= (2)式中 K ── 弹簧刚度阻尼力与运动速度成正比，与运动方向相反，即()dtt dy B f B = (3) 式中 B ── 阻尼系数将式（2）和（3）代入（1）中，可得该系统的微分方程式：()()()()t f t Ky dt t dy B dt t y d m =++22 (4) 若令 K B T B ＝──时间常数；Km T m =──时间常数。

则（4）式可写成： ()()()()()t f K t f K t y dt t dy T dt t y d T a B m==++1222 式中 KK a 1=2-7. 解：（a ）；；；（b ）2-8．543432143221432)1()()()(K K K K K K K s K K K s K s K K K s R s C +++++=τττ 2-9. (a ) 2423241321121413211)()(H G H G G G G G G G H G G G G G G G s R s C ++++++= (b ) HG G G G G G s R s C 2132211)()(++= 2-10． 22121211)()(H G H G G G G s R s C -+= 221212121)()(H G H G G G G G G s N s C c -+-=2-11．4232121213211)()(G H G G H G H G G G G G s R s C ++++= 2-12．(a ) bhdifjdifj bhfj bhdi bcdefk fj di bh abcdefg s R s C -++++++-=)()(1)()( (b ) 3431324321343136543211)1()()(H G G H G H G G G G H G G H G G G G G G G s R s C ++++++= 2-13解：前向通道：3211G G G P =， 412G G P =；回路增益：1211H G G L -=， 2322H G G L -=，243H G L -=， 3214G G G L -=，415G G L -=；特征式：41321242321211G G G G G H G H G G H G G +++++=∆，11=∆，12=∆； 4132124232121413211)(G G G G G H G H G G H G G G G G G G s ++++++=Φ 2-14 解：前向通道：3211G G G P =，342G G P =；回路增益：213211H H G G G L -=，112H G L -=，233H G L -=，互不接触回路L2和L3特征式：2131112321321H H G G H G H G H H G G G 1++++=∆，11=∆，112H G 1+=∆；21311123213211143321H H G G H G H G H H G G G 1)H G 1(G G G G G )s (++++++=Φ2-15解：先将系统结构图化简为如下形式回路增益：33211H G G G L -=，222H G L -=，113H G L -=，特征式：112233211H G H G H G G G +++=∆ C(s)/R(s):前向通道：3211G G G P =，11=∆, M(s)/N(s): 前向通道：22G P =，12=∆ E(s)/R(s): 前向通道：13=P ，112231H G H G ++=∆ 112233213211H G H G H G G G G G G )s (C R +++=Φ 1122332121H G H G H G G G G )s (N M +++=Φ 11223321112211H G H G H G G G H G H G )s (ER +++++=Φ。

自控原理习题解答(第二章)

[答2 （ 31 ） 1 ） ] (t) x(t) (t) Tx T sx(s) x (s) 1 1 1 T x (s) 1 T s 1 s T 1 t 1 T 1 1 T x ( t ) L x (s) L e 1 s T T
答2 4(c)
e y (s) e x (s) C2 1 1 I(s) R 1 R2 C1s C 2s R 2 C 1 C 2 s 2 C 1s 1 R 2 C1 C 2 s C1 2 (R1 R 2 )C1C 2 s C 2 s C1s (R1 R 2 )C1C 2 s C 2 C1 R 2 C1 C 2 s C1 (R1 R 2 )C1C 2 s C 2 C1 (R1 R 2 )C1C 2 s C 2 C1 R 2 C1 C 2 C1 s K d Td s C 2 C1 C 2 C1 K (R1 R 2 )C1C 2 s (R1 R 2 )C1C 2 s Td s 1 T s 1 1 1 C 2 C1 C 2 C1 为实际微分环节惯性环节 1 I(s) （R 2 ) C 2s
X(s) G1 G1 H3 H2 H1
-
Y(s) G2
G3
G4 X(s)
G1
-
-
G2 H3
-
Y(s) G3 G4
-
H2
G4 H3
1 2e 2t e t cos 3t 3s2 2s 8 8 A s 1 2 s(s 2)(s 2s 4) s 0 2 4 3s2 2s 8 B (s 2) 2 2 s(s 2)(s 2s 4) s 2

自动控制原理第二章课后习题答案（免费）

⾃动控制原理第⼆章课后习题答案（免费）⾃动控制原理第⼆章课后习题答案（免费）离散系统作业注明：*为选做题2-1 试求下列函数的Z 变换（1）()E z L =();n e t a = 解：01()[()]1k k k z E z L e t a z z z aa∞-=====--∑ （2） ();at e t e -= 解：12211()[()][]1...1atakT k aT aT aTaT k z E z L e t L ee z e z e z z e e z∞----------=====+++==--∑2-2 试求下列函数的终值：（1）112();(1)Tz E z z --=-解： 11111()(1)()1lim lim lim t z z Tz f t z E z z---→∞→→=-==∞- （2）2()(0.8)(0.1)z E z z z =--。

解：211(1)()(1)()0(0.8)(0.1)lim lim lim t z z z z f t z E z z z →∞→→-=-==--2-3* 已知()(())E z L e t =,试证明下列关系成⽴：（1）[()][];n z L a e t E a=证明：()()nn E z e nT z∞-==∑00()()()()[()]n n n n n n z z E e nT e nT a z L a e t a a ∞∞--=====∑∑ （2）()[()];dE z L te t TzT dz=-为采样周期。

证明：11100[()]()()()()()()()()()nn n n n n n n n n L te t nT e nT zTz ne nT z dE z de nT z dz dz e nT n zne nT z ∞∞---==∞-=∞∞----======-=-∑∑∑∑∑所以：()[()]dE z L te t Tzdz=- 2-4 试求下图闭环离散系统的脉冲传递函数()z Φ或输出z 变换()C z 。

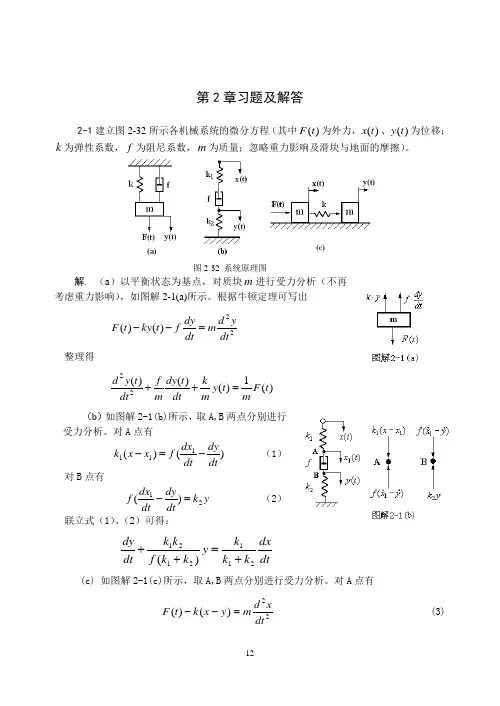
自动控制原理第2章课后习题及解答

+
1 C2R2
uc
=
du
2 r
dt 2
+
2 CR
dur dt
+
1 C2R2
ur
(c) 由图解 2-2（c）可写出
Ur (= s) R1 [I1(s) + I2 (s)] + (Ls + R2 )I2 (s) (6)
1 Cs
I1
(s)
=
(Ls
+
R2
)I2
(s)
(7)
U c (s) = R2 I 2 (s)
第 2 章习题及解答
2-1 建立图 2-32 所示各机械系统的微分方程（其中 F (t) 为外力，x(t) 、y(t) 为位移； k 为弹性系数， f 为阻尼系数， m 为质量；忽略重力影响及滑块与地面的摩擦）。
图 2-32 系统原理图
解. （a）以平衡状态为基点，对质块 m 进行受力分析（不再
考虑重力影响），如图解 2-1(a)所示。根据牛顿定理可写出
2
2
X (s=)
e−s s2
(s
+
1) 2
−
e−3s s2
(2s
+
1) 2
（c） x(t) = a + (b − a)(t − t1 ) − (b − c)(t − t2 ) − c(t − t3 ) X (s) = 1 [a + (b − a)e−t1s − (b − c)e−t2s − ce−t3s ] s
k1k 2
k1 k2 k1
图解 2-3(a)
(b) 由图可写出
Uc (s) =
Ur (s)
R2

自动控制原理第二版课后答案第二章精选全文完整版

x kx ，简记为
y kx 。
若非线性函数有两个自变量，如 z f (x, y) ，则在
平衡点处可展成（忽略高次项）
f
f
z xv
|( x0 , y0 )
x y |(x0 , y0 )
y
经过上述线性化后，就把非线性关系变成了线性关系，从而使问题大大简化。但对于如图（d）所示的强非线性，只能采用第七章的非线性理论来分析。对于线性系统，可采用叠加原理来分析系统。
Eb (s) Kbsm (s)
Js2 m(s) Mm fsm(s)
c
(s)
1
i
m
(s)
45
系统各元部件的动态结构图
传递函数是在零初始条件下建立的，因此，它只是系统的零状态模型，有一定的局限性，但它有现实意义，而且容易实现。
26
三、典型元器件的传递函数
1. 电位器
1 2
max
E
Θs
U s
K
U
K E
max
27
2. 电位器电桥
1
2
E
K1p1
K1 p 2
U
Θ 1
s
Θ
K1 p
Θ 2
s
U s
28
3.齿轮
传动比 i N2 N1
G2(s)
两个或两个以上的方框，具有同一个输入信号，并以各方框输出信号的代数和作为输出信号，这种形
式的连接称为并联连接。
41
3. 反馈连接
R(s)
－
C(s) G(s)
H(s)
一个方框的输出信号输入到另一个方框后，得到的输出再返回到这个方框的输入端，构成输入信号的一部分。这种连接形式称为反馈连接。

自动控制原理_孟华_习题答案

自动控制原理课后习题答案第二章2.1 试分别写出图2.68中各无源电路的输入u r(t)与输出u c(t)之间的微分方程。

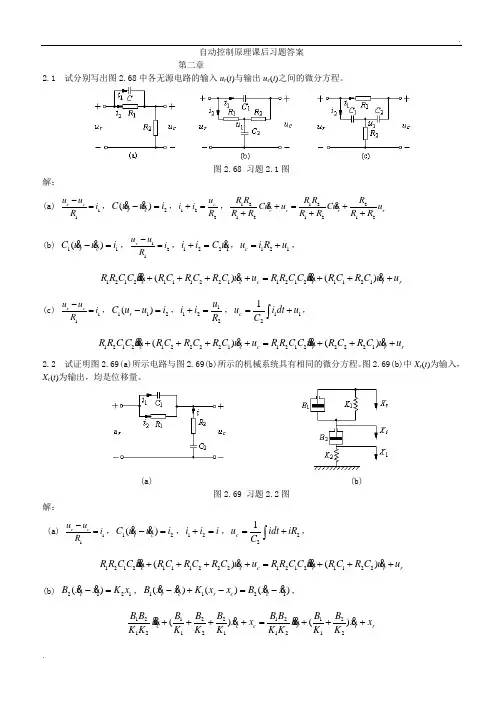
图2.68 习题2.1图解：(a)11r cu uiR-=，2()r cC u u i-=&&，122cui iR+=，12122121212c c r rR R R R RCu u Cu uR R R R R R+=++++&&(b)11()r cC u u i-=&&，121ru uiR-=，1221i i C u+=&，121cu i R u=+，121211122112121121()()c c c r r rR R C C u R C R C R C u u R R C C u R C R C u u++++=+++&&&&&&(c)11r cu uiR-=，112()rC u u i-=，1122ui iR+=，1121cu i dt uC=+⎰，121212222112122221()()c c c r r rR R C C u R C R C R C u u R R C C u R C R C u u++++=+++&&&&&&2.2 试证明图2.69(a)所示电路与图2.69(b)所示的机械系统具有相同的微分方程。

图2.69(b)中X r(t)为输入，X c(t)为输出，均是位移量。

(a) (b)图2.69 习题2.2图解：(a)11r cu uiR-=，12()r cC u u i-=&&，12i i i+=，221cu idt iRC=+⎰，121211122212121122()()c c c r r rR R C C u R C R C R C u u R R C C u R C R C u u++++=+++&&&&&&(b)2121()cB x x K x-=&&，1121()()()r c r c cB x x K x x B x x-+-=-&&&&，121221212121211212()()c c c r r rB B B B B B B B Bx x x x x xK K K K K K K K K++++=+++&&&&&&2.3 试分别求出图2.70中各有源电路的输入u r (t )与输出u c (t )之间的微分方程。

自动控制原理课后答案第2章

2
最大优点是通过梅逊增益公式可以很方便快捷地求出系统的传递函数。使用这种方法的关键在于对系统回环的判断是否正确。
表 2-1 系统结构图等效变换基本规则
3
原方框图
R
等效方框图
C
说明
C
串联等效
G1 ( s)
G2 (s )
R
G1 (s )G2 ( s )
C ( s) G1 ( s)G2 ( s) R( s )
G (s )
C
E ( s ) R ( s) H ( s )C ( s)

H (s ) H (s )
1
R( s ) H (s ) (1)C ( s )
4. 结构图与信号流图控制系统的结构图和信号流图，都是描述系统中各种信号传递关系的数学图形。应用结构图和信号流图，可以简化复杂的控制系统的分析和设计。但是，信号流图只适用于线性系统。（1）结构图系统结构图是系统中各个环节的函数功能和信号流向的图形表示，由环节（方框）、信号线、引出点和比较点组成。系统结构图可以按如下步骤绘出： ① 考虑负载效应，建立控制系统各元部件的微分方程； ② 对各元部件的微分方程进行拉氏变换，写出其传递函数并画出相应的环节单元和比较点单元； ③ 从与系统输入量有关的比较点开始，依据信号流向，把各元部件的结构图连接起来，置系统输出量于右端，便得到系统结构图。（2）信号流图信号流图是一种表达线性代数方程组结构的信号传递网络，由节点和支路组成，其与结构图本质一样，只是形式不同。为了便于描述信号流图的特征，常用的名词术语有： ① 源节点：只有输出支路的节点； ② 汇节点：只有输入支路的节点； ③ 混合节点：既有输入支路，又有输出支路的节点； ④ 前向通道：从源节点到汇接点之间，与每个节点仅相交一次的通路； ⑤ 回路：起于并终于同一节点，且与其他任何节点相交不多于一次的闭合通路； ⑥ 不接触回路：相互之间无公共节点的回路。信号流图的绘制可以根据系统微分方程绘制，也可以从系统的结构图按照一定的对应关

自动控制原理课后习题答案第二章资料讲解

第二章2-3试证明图2-5(ａ)的电网络与(b)的机械系统有相同的数学模型。

分析首先需要对两个不同的系统分别求解各自的微分表达式，然后两者进行对比，找出两者之间系数的对应关系。

对于电网络，在求微分方程时，关键就是将元件利用复阻抗表示，然后利用电压、电阻和电流之间的关系推导系统的传递函数，然后变换成微分方程的形式，对于机械系统，关键就是系统的力学分析，然后利用牛顿定律列出系统的方程，最后联立求微分方程。

证明：(a)根据复阻抗概念可得：2221212112212211212112212122111()1()111oiR u C s R R C C s R C R C R C s R u R R C C s R C R C R C C sR C s R C s+++++==+++++++即220012121122121212112222()()i i o id u du d u duR R C C R C R C R C u R R C C R C R C u dt dt dt dt++++=+++取A 、B 两点进行受力分析，可得：o 112()()()i o i o dx dx dx dx f K x x f dt dt dt dt -+-=- o 22()dx dxf K x dt dt -= 整理可得：2212111221121212211222()()o o i i o id x dx d x dx f f f K f K f K K K x f f f K f K K K x dt dt dt dt ++++=+++经比较可以看出，电网络（a ）和机械系统（b ）两者参数的相似关系为1112221211,,,K f R K f R C C ::::2-5 设初始条件均为零，试用拉氏变换法求解下列微分方程式，并概略绘制x(t)曲线，指出各方程式的模态。

(1) ;)()(2t t x t x =+&(２)）。

自动控制原理参考答案-第2章

H1
La ⎧ ⎪Tl = R a ⎪ JRa ⎪ ⎪Tm = C C e m ⎪ ⎨ ⎪ K = 2k1 H 0 ⎪ 1 k2 ⎪ 2F H 0 ⎪ ⎪T1 = k2 ⎩
题 2-8：试用动态结构图简化方法求解题 2-8 图所示两系统的传递函数。
u2
L R ia
+
u i(t)
+
u d (t)
+
Ea
M m(t)
J1
f1 r 1 f2
-
-
-
ω1 r2
M c(t)
+ if 题 2-5 图
ω2
J2
电枢控制直流电动机拖动开环系统
(1) ud (t ) = 2.34U 2 {0.82 − 0.57[ K1ui (t ) − 35o ]} = 2.34U 2 {1.168 − 0.57 K1ui (t )} (2) 参照教材 38 页图 2-24 (3) 参照教材式(2-4)、(2-5)、(2-6)、(2-17) 2.73U 2 ⎧ ′ ( s) = M c ( s) / i ⎧M c − 1.34 K1U 2U i ( s) ⎪U d ( s ) = s ⎪ ⎪ ⎪i = r2 / r1 ⎪ LsI ( s ) + RI ( s ) + C Ω ( s ) = U ( s ) 其中， ⎨ a e 1 d ⎨ a 2 ⎪ J = J1 + J 2 / i ⎪ M ( s ) = Cm I a ( s ) ⎪ f = f + f / i2 ⎪ 1 2 ⎩ ′ ( s) ⎪ ⎩ JsΩ1 ( s ) + f Ω1 ( s ) = M ( s ) − M c
⇒
[iJLs 3 + (iJR + ifL) s 2 + (ifR + iCmCe ) s ]Ω1 ( s ) = 2.73CmU 2 − 1.34 K1CmU 2 sU i ( s ) − ( Ls + R ) M c ( s )

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

于就是,得特征式为
从输入R到输出C的前向通路共有4条,其前向通路总增益以及余因子式分别为
因此,传递函数为
2-5试简化图2-5中的系统结构图,并求传递函数C(s)/R(s )与C(s)/N(s)。
图2-5
解:仅考虑输入R(S)作用系统时,单独回路2个,即
两个互不接触的回路没有,于就是,得特征式为
从输入R到输出C的前向通路共有1条,其前向通路总增益以及余因子式分别为
第二章控制系统的数学模型
2.1RC无源网络电路图如图2－1所示,试采用复数阻抗法画出系统结构图,并求传递函数Uc(s)/Ur(s)。
图2－1
解:在线性电路的计算中,引入了复阻抗的概念,则电压、电流、复阻抗之间的关系,满足广义的欧姆定律。即:
如果二端元件就是电阻R、电容C或电感L,则复阻抗Z(s)分别就是R、1/Cs或Ls。
低频段 ,斜率-20db/dec,延长线过1,2log10点,过 =0、2后,斜率为-40db/dec,过 =10后,斜率为-60db/dec
确定系统的截止频率 C与相角裕度。
确定系统的截止频率 C:
通过作图可以瞧出截止频率在1与2之间,在通过试根的方法确定稍精确的值为1、4
确定系统的相角裕度:
=1800+ =1800-900-arctan5 -arctan0、1 =900-81、880-7、970=0、150
5、4某位置控制系统的结构如图1。试绘制系统开环的伯德图,并确定系统的相位稳定裕量。
, =4, =10
低频段 ,斜率-20db/dec,过1,2log10点,过 =4后,斜率为-40db/dec,过 =10后,斜率为-60db/dec
终点: ,
(2)求幅相曲线与负实轴的交点
,
P=0,N-=1, N+=0,R=2(N+-N-)=-2,Z=P-2N=2
由奈氏判据知,闭环系统就是不稳定的。
5、3已知一单位负反馈系统开环传递函数
作系统开环对数幅频L(),有简要的计算说明画图过程,并确定系统的截止频率 C与相角裕度。
, =0、2, =10
两个互不接触的回路,于就是,得特征式为
从输入R到输出C的前向通路共有1条,其前向通路总增益以及余因子式分别为
因此,传递函数为
E(s)/R(s):单独回路3个,即
两个互不接触的回路,于就是,得特征式为
从输入R到输出E的前向通路共有2条,其前向通路总增益以及余因子式分别为
因此,传递函为
第三章线性系统的时域分析法
解:
(1)确定起点与终点
,故初始相角为-90,
终点: ,
(2)求幅相曲线与负实轴的交点
,
P=0,N-=1, N+=0,R=2(N+-N-)=-2,Z=P-2N=2
由奈氏判据知,闭环系统就是不稳定的。
5、2已知系统的开环传函用奈氏判据(画出奈氏曲线)判别闭环系统的稳定性。
解:
(1)确定起点与终点
,故初始相角为-180,
解本例就是应用劳斯判据判断系统稳定性的一种特殊情况。如果在劳斯行列表中某一行的第一列项等于零,但其余各项不等于零或没有,这时可用一个很小的正数ε来代替为零的一项,从而可使劳斯行列表继续算下去。
劳斯行列式为
由劳斯行列表可见,第三行第一列系数为零,可用一个很小的正数ε来代替;第四行第一列系数为(2ε+2/ε,当ε趋于零时为正数;第五行第一列系数为(－4ε－4－5ε2)/(2ε+2),当ε趋于零时为。由于第一列变号两次,故有两个根在右半s平面,所以系统就是不稳定的。
因此,传递函数为
仅考虑输入N(S)作用系统时,单独回路2个,即
两个互不接触的回路没有,于就是,得特征式为
从输入N到输出C的前向通路共有2条,其前向通路总增益以及余因子式分别为
因此,传递函数为
2-6用梅逊增益公式求传递函数C(s)/R(s)与E(s)/R(s)。
图2-6
解:C(s)/R(s):单独回路3个,即
3-1设二阶控制系统的单位阶跃响应曲线如图3-1所示。试确定系统的传递函数。
图3-1二阶控制系统的单位阶跃响应
解在单位阶跃作用下响应的稳态值为3,故此系统的增益不就是1,而就是3。系统模型为
然后由响应的、及相应公式,即可换算出、。
(s)
由公式得
换算求解得: 、
3-2设系统如图3-2所示。如果要求系统的超调量等于 ,峰值时间等于0、8s,试确定增益K1与速度反馈系数Kt。同时,确定在此K1与Kt数值下系统的延迟时间、上升时间与调节时间。
图3-2
解由图示得闭环特征方程为
即
,
由已知条件
解得
于就是
3-3已知系统特征方程式为试用劳斯判据判断系统的稳定情况。
解劳斯表为
1 18
8 16
由于特征方程式中所有系数均为正值,且劳斯行列表左端第一列的所有项均具有正号,满足系统稳定的充分与必要条件,所以系统就是稳定的。
3-4已知系统特征方程为试判断系统稳定性。
(1)用复阻抗写电路方程式:
(2)将以上四式用方框图表示,并相互连接即得RC网络结构图,见图2－1(a)。
2－1(a)。
(3)用梅逊公式直接由图2－1(a)写出传递函数Uc(s)/Ur(s)。
独立回路有三个:
回路相互不接触的情况只有L1与L2两个回路。则
由上式可写出特征式为:
通向前路只有一条
由于G1与所有回路L1,L2,L3都有公共支路,属于相互有接触,则余子式为
Δ1=1
代入梅逊公式得传递函数
2-2已知系统结构图如图2-2所示,试用化简法求传递函数C(s)/R(s)。
图2－2
解:(1)首先将含有G2的前向通路上的分支点前移,移到下面的回环之外。如图2-2(a)所示。
(2)将反馈环与并连部分用代数方法化简,得图2-2(b)。
(3)最后将两个方框串联相乘得图2-2(c)。
图2-2系统结构图的简化
2、3化简动态结构图,求C(s)/R(s)
图2－3
解:单独回路1个,即
两个互不接触的回路没有
于就是,得特征式为
从输入R到输出C的前向通路共有2条,其前向通路传递函数以及余因子式分别为
因此,传递函数为
2、4用梅森公式求系统传递函数。
图2－4
解:单独回路5个,即
两个互不接触的回路没有
3、5
解;在求解系统的稳态误差前必须判定系统就是否稳定;
系统特征方程为由劳斯判据判断
劳斯行列式为
由于特征方程式中所有系数均为正值,且劳斯行列表左端第一列的所有项均具有正号,满足系统稳定的充分与必要条件,所以系统就是稳定的。
可知v=1,K=10
当,
当
第五章线性系统的频域分析法
5、1已知系统的开环传函 ,用奈氏判据(画出奈氏曲线)判别闭环系统的稳定性。