导数与函数放缩问题之切线法放缩

导数中放缩法(切线放缩、对数均值不等式)导数证明中的常用放缩在导数证明中，常用的放缩方法有切线放缩、对数放缩、指数放缩、指对放缩和三角函数放缩等。

其中，常用的放缩公式包括对数放缩和指数放缩。

一、常用放缩公式1.对数放缩对数放缩常常可以将一个函数放缩成一次函数或双撇函数，常用的对数放缩公式包括：lnx≤x-1，lnx<x，ln(1+x)≤xlnxx-1/x，x>1lnxx/2，0<x<1lnx≤x^2-x，ln(1+x)≤x-x^2/2，-1<x<∞ln(1+x)≥x/(1+x)，ln(1+x)>x/2，x>02.指数放缩指数放缩常常可以将一个函数放缩成一次函数或二次函数，常用的指数放缩公式包括：ex≥x+1，ex>x，ex≥ex，x≤0ex<1-x，ex<1-x+x^2/2，x<0ex≥1+x+x^2，ex≥1+x+x^2+x^3，x>03.指对放缩指对放缩常常可以将一个函数的导数放缩成一个常数，常用的指对放缩公式包括：ex-lnx≥(x+1)-(x-1)/2，x>04.三角函数放缩三角函数放缩常常可以将一个函数放缩成一个三角函数或二次函数，常用的三角函数放缩公式包括：XXX<x<tanx，sinx≥x-x^2，-1≤x≤1cosx≤1-sin^2x，-1≤x≤1二、经典例题以函数f(x)=lnx+ax^2+(2a+1)x为例，讨论其单调性和当a<0时的最大值。

1) 解f(x)的定义域为(0,∞)，求导得f'(x)=1/x+2ax+2a+1.当a≥-1/2时，f'(x)>0，因此f(x)在(0,∞)上单调递增；当a<-1/2时，f'(x)<0，因此f(x)在(0,∞)上单调递减。

2) 当a0，因此g(x)在(0,∞)上单调递增，且有g(x)≤g(1)=ln1-2/3=-2/3.又因为f(x)可以表示为f(x)=g(x)+(2a+1)x+ax^2+2/3x，因此有f(x)≤g(1)+(2a+1)x+ax^2+2/3x=-2/3+(2a+1)x+ax^2+2/3x=2/3x+ax^2+(2a+1)x-2/3.当2/3x+ax^2+(2a+1)x-2/3取到最大值时，有x=-(2a+1)/(2a),此时f(x)的最大值为-2/3+(2a+1)^2/(4a)-a(2a+1)^2/(4a)=-3/4a。

切线放缩的原理
切线放缩的原理是基于函数的二阶导数。

如果函数在某点处的二阶导数大于0，则函数在该点处向上凸；如果二阶导数小于0，则函数在该点处向下凸；如果二阶导数为0，则该点可能是函数的拐点。

切线放缩是优化算法中的一种方法，通过限制函数的一些特定性质来确定函数的最小值或最大值。

例如，对于函数f(x) = x^2 + 3x - 5，我们可以使用切线放缩法来寻找其在定义域[-2,2]上的最小值。

由于函数在定义域内处处向上凸，我们可以选择一个切线使其与函数图像相切，然后将这个切线向左右两边移动，直到它与函数图像的交点构成的区间完全包含在定义域内，从而找到函数的最小值或最大值。

函数与导数—导数中的放缩问题专题综述放缩法是解决函数不等式问题的利器，导数压轴题中的函数往往是指数、对数与其他函数综合，或者指对数并存的超越函数，有时直接构造出的函数难以直接求出最值，需要借助放缩解决.利用导数判断函数单调性、解决函数零点问题、不等式证明等问题中都会用到放缩法，使问题难度降低.常用的放缩方式有：①常用不等式放缩：指数放缩、对数放缩、三角放缩；②利用已知题目信息放缩；③根据已知参数范围或常识，减少变量，适当放缩；③利用单调性放缩；④利用基本不等式放缩： 若0a b >>，则211ln ln 2a b a bb ab a b a b-+<<<<-+；⑤由数值大小关系直接放缩，做题时灵活运用.本专题就前3种，重点探究.专题探究探究1：利用不等式放缩函数中有指数、对数、三角函数时，直接求导，导数不等式无法解出，根据函数结构，选择不等式进行放缩，使函数简单化. 常用不等式有：（1）三角函数放缩：①0,,sin tan 2x x x x π⎛⎫∀∈<< ⎪⎝⎭；②21sin 2x x x ≥-；③22111cos 1sin 22x x x -≤≤-（2）指数放缩：①1x e x ≥+；②x e ex ≥（1,y x y ex =+=为函数x y e =图象的两条切线）；③()101xe x x ≤≤-；④()10x e x x≤-< （3）对数放缩：①11ln 1x x x -≤≤-；②ln x x e ≤；③1ln x ex ≥-；（1,xy x y e =-=为函数ln y x =图象的两条切线）（4）指对放缩：()()ln 112xe x x x ->+--=(2021安徽省合肥市联考) 已知函数()(ln ),.xe f x a x x a R x=--∈（1）当0a >时，讨论函数()f x 的单调性；（2）当1a =-时，函数1()()()x g x f x x e mx x =+++满足：对任意(0,)x ∈+∞，都有()1g x 恒成立，求实数m 的取值范围．【审题视点】第（2）问显化函数()g x ，恒成立问题回顾常用的方法（专题1.3.7）：分离参数、含参讨论单调性等方法，由解析式的具体结构确定方法与细节.【思维引导】分离参数以后，函数中有指、对结构，若直接通过求导判断单调性求最值，方法较困难，利用不等关系1x e x ≥+，得ln ln 1x x e x x +≥++，使难度大大降低.【规范解析】解：（1）()f x 的定义域是(0,)+∞，22()(1)()x x x a xe e ax e x f x a x x x -+-'=--=，当0a >，0x >时，令()0f x '>，则1x <∴()f x 在(0,1)上单调递增，在(1,)+∞上单调递减；（2）当1a =-时，1()()()ln (1)x x g x f x x e mx xe x m x x=+++=-++，()()0,,1x g x ∀∈+∞≥即ln 1ln 1ln 11x x x x xe x e m x x++-+--=-，1.恒成立问题求参：分离参数构造函数求最值；2.构造的函数中有ln x 、ln x x e +，通过求导判断单调性求最值较困难，通过常用不等关系1xe x ≥+，进行放缩,是函数简单化.设()1x F x e x =--，则()1x F x e '=-，令()0F x '>，则0x >∴()f x 在()0,+∞上单调递增，在(),0-∞上单调递减∴()(0)0F x F =，即1(x e x +当且仅当0x =时“=”成立)，故ln ln 1(x x e x x +++当且仅当ln 0x x +=时“=”成立)， ()ln G x x x =+在(0,)+∞上是增函数，且11()10G e e=-<，(1)10G =>，故存在01(,1)x e∈使得ln 0x x +=成立，故ln 1ln 1ln (ln 1)112x x x e x x x x x++-+-++--=-（当且仅当0x x =时“=”成立），∴2m -，即m 的取值范围是[2,).-+∞【探究总结】常见的不等关系要灵活运用，解题时函数结构复杂，可考虑运用上述不等式进行放缩，使问题简答化.但不等式1,,ln 1,ln xxx e x e ex x x x e≥+≥≤-≤，从图象的角度看，是以直代曲，放缩的程度大，容易出现误差，在使用时要注意.另外若是求参数取值范围问题，要考虑不等式中的等号能否取到.(2021山东省泰安市一模) 已知函数()()ln 2xf x e x k -=-，（k 为常数， 2.718e =⋅⋅⋅是自然对数的底数），曲线()y f x =在点()()1,1f 处的切线与y 轴垂直.（1）求()f x 的单调区间；（2）设()()1ln 1xx x g x e-+=,对任意0x >，证明：()()21x x x g x e e -+<+. 探究2：利用已证结论放缩1.对使用过得不等关系，构造函数证明成立；2.利用不等关系进行替换.恒成立求取值范围的问题，放缩以后，要确保不等式中等号能否取到解答题的上一问中证明的不等式，或者推导过程中证明出的结论，为后续的证明提供放缩的依据.需证明的不等式为关于n 的多项式的和或不等式结构复杂，利用已证结论，进行放缩，使不等式化繁为简，便于构造函数求最值.(2021湖南省郴州市模拟) 已知函数()e (1)ln(1) 1.x f x x x =-++-（1）当0x >时，证明：()0f x >；（2）已知数列{}n a 的通项公式为1e 1nn n na n -=+，证明：12ln (1).n a a a n ++⋅⋅⋅+>+ 【审题视点】第（2）问，出现数列的前n 项和，且不能用常规的求和方法求和，借助第一问的结论对n a 的通项公式进行放缩，便于求和.【思维引导】对第一问的不等式进行变形，观察n a 的结构，进行放缩，能够用已知方法求和.【规范解析】解：（1）由题意得 ()()ln(1)10x f x e x x '=-+->， 设()ln(1)1x g x e x =-+-，则1(1)1()11x xe x g x e x x +-'=-=++， 当0x >时， 1x e >，11x +>，则(1)1x e x +>则(1)1()01x e x g x x +-'=>+， ()g x ∴在()0,+∞上单调递增，故()()00g x g >=，即()0f x '> ()f x ∴在()0,+∞上单调递增，∴当0x >时，()(0)0f x f >=，即()0f x >（2）由（1）知：当0x >时，()(1)ln(1)10x f x e x x =-++->，即1ln(1)1x e x x ->++ 令1x n=，则11ln()1nne n n n n -+>+，12231ln ln ln12n n a a a n++++>+++ 231ln()ln(1)12n n n+=⨯⨯⨯=+ ∴12ln (1)n a a a n ++⋅⋅⋅+>+【探究总结】函数中证明与n 有关的求和问题，或不等式证明问题，要仔细观察不等式结构特点，往往会利用前一问的结论，或者解题过程中的结论.利用已证结论，进行放缩，化繁为简，证明不等式的成立.(2021广东省东莞市联考) 已知函数()ln (1),(0)f x x a x a =-->（ 2.718e ≈即自然对数的底数）.（1）若函数()f x 在()1,+∞上是单调减函数，求实数a 的取值范围； （2）在（1）的条件下，当n N +∈时，证明：2311111111.2222n e ⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭探究3：利用已知参数范围或常识放缩函数解析中含有参数，且已知参数范围，证明不等式成立，可以从参数的范围入手，使参数取确定的值或利用单调性、其它不等关系，对不等式进行放缩，减少变量，使函数结构简单，易于判断单调性.(2021河北省石家庄联考) 已知函数()(2).x f x e k x =-+（1）讨论函数()f x 的单调性；（2）证明：当0k e <<时，()(1ln )0.f x k x x ++->【审题视点】已知参数范围，证明不等式成立，且函数指对结构都有，若含参讨论难度大，可能要借助放缩，化繁为简.【思维引导】1.对已证不等式进行变形，变形为与n a 通项公式相似的结构；2.对自变量进行替换，得出新的不等式.利用不等式性质进行求和，实现放缩，证明结论.第（2）问不等式的证明，函数中有x e ，ln x ，构造函数求导，含参讨论解导数不等式较困难，可巧妙利用参数的范围，参数取确定的值，进行放缩，求不含参函数的最值较为简单.【规范解析】解：（1）由题意得 ()e .x f x k '=- ①当0k 时，()e 0x f x k '=->，∴函数()f x 在(,)-∞+∞上单调递增；②当0k >时，令()e 0x f x k '=-> 得ln x k >，则()g x '在(0,)+∞上单调递增，且(1)0g '= 当(0,1)x ∈时，()0g x '< 当(1,)x ∈+∞时，()0g x '>)0，10⎫->⎪⎭∴当0k e <<时，()(1ln )0.f x k x x ++->【探究总结】不等式的证明问题中含有参数，若直接构造函数含参讨论，难以解决的情况下，为避开讨论，可以在参数给定的范围内，结合不等式的结构进行第一步的放缩，达到消参的目的，转化为证明不含参的不等式.若不等式的结构依然复杂，在利用常用不等关系、已证结论等方法进一步放缩.(2021湖北省荆州市高三模拟) 已知函数()ln(2).x m f x e x -=-（1）设1x =是函数()f x 的极值点，求m 的值并讨论()f x 的单调性； （2）当2m 时，证明：()ln 2.f x >-专题升华导数解答题中函数多以xe 、ln x 型的函数与其他函数结合的形式出现，考查零点问题、不等式证明问题、恒成立问题等方向时，如果利用常规方法处理时，因函数结构复杂求导判断单调性难度较大，通过放缩将难以处理的函数转化为较为简单的函数进行处理.放缩法较为灵活，要根据不等式的结构、形式等特征，使条件与结论建立联系，选择适当的方法是关键. 1.积累常见的不等结论：如探究1中提及的不等式，解题时需构造函数，证明其正确性，再进行放缩.利用不等式进行放缩，体现了数学中的化归与转化思想，也体现了处理数学问题时以直代曲、以曲代曲的方法.2.巧用已证不等式，顺水推舟：利用已证不等式(或结论) “服务”于后续问题的求解，这类题目最明显的“暗示”，即为证明一个类似于数列求和的不等式，需利用已证不等式进行逐项替换放缩.若题目的第一问证明不等式，在后续解题时，留意是否会利用已证结论.3.已知参数范围：含参不等式的证明时，若因为参数的存在使函数讨论非常复杂，可考虑结合参数范围及其它结论进行放缩.4.其他放缩方法：除了上述三种难度较大的放缩方法以外，单调性、已知结论、基本不等式等.如利用基本不等式进行放缩，化曲为直，()202x x +=≥；和积互化等.不仅仅应用于简化不等式，在解题过程中，也可能用放缩证明代数式的值.长干行·其一[唐]李白妾发初覆额，折花门前剧。

割线放缩的原理割线放缩是一种常用的数学方法，用于求解函数的极限和导数。

它的原理是通过逐渐缩小自变量的取值范围，从而逼近函数的极限值或导数值。

在本文中，我将详细介绍割线放缩的原理及其应用。

割线放缩的基本思想是利用函数的局部性质来逼近全局性质。

首先，我们选取函数上两个点，这两个点分别位于自变量取值范围的两个极限点，我们称之为割线的两个端点。

然后，通过连接这两个点，得到一条割线。

接下来，我们将自变量的取值范围逐渐缩小，并计算割线与函数曲线的交点。

通过不断缩小取值范围，我们可以逼近函数曲线上的某一点，从而求得函数的极限值或导数值。

割线放缩的原理可以用以下步骤表示：步骤一：选择割线的两个端点。

这两个点应该分别位于自变量取值范围的两个极限点，并且函数在这两个点上有定义。

步骤二：计算割线的斜率。

割线的斜率可以通过两个端点的坐标计算得到。

步骤三：通过割线的斜率和某一端点的坐标，得到割线的方程。

步骤四：计算割线与函数曲线的交点。

将割线的方程代入函数的方程，解方程得到交点的坐标。

步骤五：根据需要，继续缩小自变量的取值范围，重复步骤二至步骤四，直到达到所需的精度。

割线放缩在求解函数的极限和导数时有广泛的应用。

在求解函数的极限时，我们可以通过选取两个趋近于极限点的端点，来逼近极限值。

在求解函数的导数时，我们可以通过选取两个极限点附近的端点，来逼近导数值。

举个例子来说明割线放缩的应用。

假设我们要求解函数f(x) = x^2 在点 x = 2 处的导数。

我们可以选取两个端点分别为 x = 1 和 x = 3，然后计算割线的斜率。

假设割线的斜率为k，那么割线的方程可以表示为 y = kx + b，其中 b 是一个常数。

接下来，我们将割线的方程代入函数的方程，得到方程 kx + b = x^2。

通过解这个方程，我们可以得到割线与函数曲线的交点坐标。

最后，我们可以通过不断缩小自变量的取值范围，重复上述过程，来逼近导数值。

割线放缩是一种简单而有效的数学方法，可以用于求解函数的极限和导数。

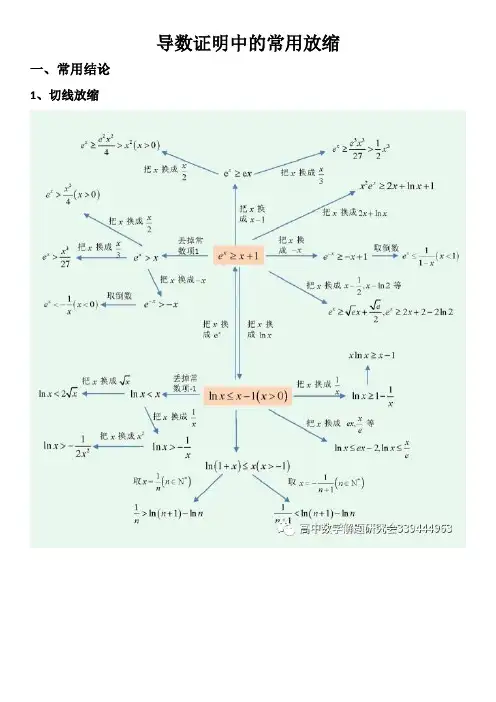
导数证明中的常用放缩一、常用结论1、切线放缩2、其它对数放缩（对数均值不等式）3、常用放缩公式：（考试时需给出证明过程）第一组：对数放缩（放缩成一次函数）ln 1x x ≤-，ln x x <，()ln 1x x +≤ （放缩成双撇函数）()11ln 12x x x x ⎛⎫<-> ⎪⎝⎭，()11ln 012x x x x ⎛⎫>-<< ⎪⎝⎭， )ln 1x x<>，)ln 01x x ><<， （放缩成二次函数）2ln x x x ≤-，()()21ln 1102x x x x +≤--<<，()()21ln 102x x x x +≥-> （放缩成类反比例函数）1ln 1x x≥-，()()21ln 11x x x x ->>+，()()21ln 011x x x x -<<<+，()ln 11x x x +≥+，()()2ln 101x x x x +>>+，()()2ln 101x x x x+<<+ 第二组：指数放缩（放缩成一次函数）1x e x ≥+，x e x >，x e ex ≥， （放缩成类反比例函数）()101x e x x ≤≤-，()10x e x x<-<， （放缩成二次函数）()21102x e x x x ≥++>，2311126x e x x x ≥+++， 第三组：指对放缩()()ln 112x e x x x -≥+--=第四组：三角函数放缩()sin tan 0x x x x <<>，21sin 2x x x ≥-，22111cos 1sin 22x x x -≤≤-. 第五组：以直线1y x =-为切线的函数ln y x =，11x y e -=-，2y x x =-，11y x=-，ln y x x =.二、基础练习：练习题组一练习题组二：二、经典例题：母题 (2017·全国Ⅲ)已知函数f (x )＝ln x ＋ax 2＋(2a ＋1)x .(1)讨论f (x )的单调性；(2)当a <0时，证明f (x )≤－34a－2.(1)解 f (x )的定义域为(0，＋∞)，f ′(x )＝1x ＋2ax ＋2a ＋1＝(x ＋1)(2ax ＋1)x. 若a ≥0，则当x ∈(0，＋∞)时，f ′(x )>0，故f (x )在(0，＋∞)上单调递增．若a <0，则当x ∈⎝⎛⎭⎫0，－12a 时，f ′(x )>0； 当x ∈⎝⎛⎭⎫－12a ，＋∞时，f ′(x )<0. 故f (x )在⎝⎛⎭⎫0，－12a 上单调递增，在⎝⎛⎭⎫－12a ，＋∞上单调递减． (2)证明 由(1)知，当a <0时，f (x )在x ＝－12a 处取得最大值，最大值为f ⎝⎛⎭⎫－12a ＝ln ⎝⎛⎭⎫－12a －1－14a， 所以f (x )≤－34a －2等价于ln ⎝⎛⎭⎫－12a －1－14a ≤－34a－2， 即ln ⎝⎛⎭⎫－12a ＋12a＋1≤0. 设g (x )＝ln x －x ＋1，则g ′(x )＝1x－1. 当x ∈(0,1)时，g ′(x )>0；当x ∈(1，＋∞)时，g ′(x )<0.所以g (x )在(0,1)上单调递增，在(1，＋∞)上单调递减．故当x ＝1时，g (x )取得最大值，最大值为g (1)＝0.所以当x >0时，g (x )≤0.从而当a <0时，ln ⎝⎛⎭⎫－12a ＋12a ＋1≤0，即f (x )≤－34a－2. [子题1] 设函数f (x )＝ln x －x ＋1.证明：当x ∈(1，＋∞)时，1<x －1ln x<x . 证明 f ′(x )＝1x －1＝1－x x，x >0， 当x >1时，f ′(x )<0，f (x )单调递减，当0<x <1时，f ′(x )>0，f (x )单调递增，∴f (x )＝ln x －x ＋1≤f (1)＝0，∴ln x ≤x －1，∴当x >1时，ln x <x －1，①且ln 1x <1x－1，② 由①得，1<x －1ln x ，由②得，－ln x <1－x x， ∴ln x >x －1x ，∴x >x －1ln x， 综上所述，当x >1时，1<x －1ln x<x . [子题2] 已知函数f (x )＝e x －x 2.求证：当x >0时，e x ＋(2－e )x －1x≥ln x ＋1. 证明 设g (x )＝f (x )－(e －2)x －1＝e x －x 2－(e －2)x －1(x >0)，则g ′(x )＝e x －2x －(e －2)，设m (x )＝e x －2x －(e －2)(x >0)，则m ′(x )＝e x －2，易得g ′(x )在(0，ln 2)上单调递减，在(ln 2，＋∞)上单调递增，又g ′(0)＝3－e>0，g ′(1)＝0，由0<ln 2<1，则g ′(ln 2)<0，所以存在x 0∈(0，ln 2)，使得g ′(x 0)＝0，所以当x ∈(0，x 0)∪(1，＋∞)时，g ′(x )>0；当x ∈(x 0,1)时，g ′(x )<0.故g (x )在(0，x 0)上单调递增，在(x 0,1)上单调递减，在(1，＋∞)上单调递增，又g (0)＝g (1)＝0，所以g (x )＝e x －x 2－(e －2)x －1≥0，故当x >0时，e x ＋(2－e )x －1x≥x . 又由母题可得ln x ≤x －1，即x ≥ln x ＋1，故e x ＋(2－e )x －1x≥ln x ＋1. 规律方法 利用导数证明不等式f (x )>g (x )的基本方法(1)若f (x )与g (x )的最值易求出，可直接转化为证明f (x )min >g (x )max .(2)若f (x )与g (x )的最值不易求出，可构造函数h (x )＝f (x )－g (x )，然后根据函数h (x )的单调性或最值，证明h (x )>0.(3)通过题目中已有的或常用的不等式进行证明．(4)利用赋值法证明与正整数有关的不等式.跟踪演练1．(2018·全国Ⅰ)已知函数f (x )＝a e x －ln x －1.(1)设x ＝2是f (x )的极值点，求a ，并求f (x )的单调区间；(2)证明：当a ≥1e时，f (x )≥0. (1)解 f (x )的定义域为(0，＋∞)，f ′(x )＝a e x －1x. 由题设知，f ′(2)＝0，所以a ＝12e 2. 从而f (x )＝12e 2e x －ln x －1，f ′(x )＝12e 2e x －1x. 当0<x <2时，f ′(x )<0；当x >2时，f ′(x )>0.所以f (x )的单调递增区间为(2，＋∞)，单调递减区间为(0,2)．(2)证明 当a ≥1e 时，f (x )≥e x e－ln x －1. 设g (x )＝e x e－ln x －1(x ∈(0，＋∞))， 则g ′(x )＝e x e －1x. 当0<x <1时，g ′(x )<0；当x >1时，g ′(x )>0.所以x ＝1是g (x )的最小值点．故当x >0时，g (x )≥g (1)＝0.因此，当a ≥1e时，f (x )≥0. 2．(2020·北京市陈经纶中学模拟)已知函数f (x )＝ln x －1x－ax .若1<a <2，求证：f (x )<－1. 证明 f (x )的定义域为(0，＋∞)，为了证明f (x )<－1，即ln x －1x－ax <－1， 只需证明ln x －1－ax 2<－x ，即ln x <ax 2－x ＋1，令m (x )＝ln x －x ＋1(x >0)，则m ′(x )＝1x－1， 令m ′(x )>0，得0<x <1；令m ′(x )<0，得x >1，所以m (x )在(0,1)上单调递增，在(1，＋∞)上单调递减，所以m (x )max ＝m (1)＝0，即ln x －x ＋1≤0，则ln x ≤x －1.令n (x )＝ax 2－2x ＋2，因为1<a <2，所以Δ＝4－8a <0，所以n (x )>0恒成立，即ax 2－2x ＋2>0，所以ax 2－x ＋1>x －1.综上所述，ln x <ax 2－x ＋1，即当1<a <2时，f (x )<－1.（2017年全国新课标1·理·21）已知()()22x x f x ae a e x =+--.（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围.解析：（1）()()()()2'221211x x x x f x ae a e e ae =+--=+-若0a ≤，则()'0f x <恒成立，所以()f x 在R 上递减；若0a >，令()'0f x =，得11,ln x e x a a ==. 当1ln x a <时，()'0f x <，所以()f x 在1,ln a ⎛⎫-∞ ⎪⎝⎭上递减； 当1lnx a >时，()'0f x >，所以()f x 在1ln ,a ⎛⎫+∞ ⎪⎝⎭上递增. 综上，当0a ≤时，()f x 在R 上递减；当0a >时，()f x 在1,ln a ⎛⎫-∞ ⎪⎝⎭上递减，在1ln ,a ⎛⎫+∞ ⎪⎝⎭上递增. （2）()f x 有两个零点，必须满足()min 0f x <，即0a >，且()min 111ln1ln 0f x f a a a ⎛⎫==--< ⎪⎝⎭. 构造函数()1ln g x x x =--，0x >. 易得()1'10g x x =--<，所以()1ln g x x x =--单调递减. 又因为()10g =，所以()11111ln 01101g g a a a a a ⎛⎫--<⇔<⇔>⇔<< ⎪⎝⎭. 下面只要证明当01a <<时，()f x 有两个零点即可，为此我们先证明当0x >时，ln x x >. 事实上，构造函数()ln h x x x =-，易得()1'1h x x=-，∴()()min 11h x h ==，所以()0h x >，即ln x x >. 当01a <<时，()()22222110a ea e a a f e e e++---=++=>， ()2333333ln 121ln 11ln 10a f a a a a a a a a -⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+----=---> ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭， 其中11ln a -<，31ln ln a a a ->，所以()f x 在11,ln a ⎛⎫- ⎪⎝⎭和13ln ,ln a a a -⎛⎫ ⎪⎝⎭上各有一个零点. 故a 的取值范围是()0,1.注意：取点过程用到了常用放缩技巧。

For personal use only in study and research; not forcommercial use(高手必备）高考导数大题中最常用的放缩大法相信不少读者在做高考导数解答题时都有这样的感悟，将复杂的函数求导，再对导函数求导，再求导，然后就没有然后了......如果懂得了最常见的放缩，如：人教版课本中常用的结论⑴sin ,(0,)x x x π<∈，变形即为sin 1x x<，其几何意义为sin ,(0,)y x x π=∈上的的点与原点连线斜率小于1.⑵1x e x >+⑶ln(1)x x >+⑷ln ,0x x x e x <<>.将这些不等式简单变形如下： exx ex e x e x x x x x 1ln ,,1,1ln 11-≥≥+≥-≤≤-那么很多问题将迎刃而解。

例析：（2018年广州一模）x e x x f x x ax x f 2)(,0,1ln )(⋅≤>++=若对任意的设恒成立，求a 的取值范围。

放缩法：由可得：1+≥x e x 2)1(ln 1ln 2)1(ln )1(ln 1ln ln 22=+-++≥+-=+-=+-+x x x x x x e x x xe x x e x x x x高考中最常见的放缩法可总结如下，供大家参考。

第一组：对数放缩（放缩成一次函数）ln 1x x ≤-，ln x x <，()ln 1x x +≤ （放缩成双撇函数）()11ln 12x x x x ⎛⎫<-> ⎪⎝⎭，()11ln 012x x x x ⎛⎫>-<< ⎪⎝⎭， )ln 1x x<>，)ln 01x x ><<， （放缩成二次函数）2ln x x x ≤-，()()21ln 1102x x x x +≤--<<，()()21ln 102x x x x +≥->（放缩成类反比例函数）1ln 1x x ≥-，()()21ln 11x x x x ->>+，()()21ln 011x x x x -<<<+， ()ln 11x x x +≥+，()()2ln 101x x x x +>>+，()()2ln 101x x x x +<<+第二组：指数放缩（放缩成一次函数）1x e x ≥+，x e x >，x e ex ≥， （放缩成类反比例函数）()101x e x x ≤≤-，()10x e x x<-<， （放缩成二次函数）()21102x e x x x ≥++>，2311126x e x x x ≥+++， 第三组：指对放缩()()ln 112x e x x x -≥+--=第四组：三角函数放缩()sin tan 0x x x x <<>，21sin 2x x x ≥-，22111cos 1sin 22x x x -≤≤-. 第五组：以直线1y x =-为切线的函数ln y x =，11x y e -=-，2y x x =-，11y x =-，ln y x x =. 拓展阅读：为何高考中总是考这些超越函数呢？和x e x ln 因为高考命题专家是大学老师，他们站在高观点下看高中数学，一览无遗。

切线放缩公式大全切线放缩公式是数学中一个重要的工具，用于对函数进行线性近似。

它在微积分、几何以及物理等领域都有广泛的应用。

以下是一些常见的切线放缩公式的相关内容。

1. 切线方程的一般形式：设函数f(x)在点x=a处可导，则该点处的切线方程可以表示为：y=f(a)+f'(a)(x-a)，其中f'(a)表示函数在点x=a处的导数。

2. 切线拟合：当函数f(x)在点x=a处不可导时，我们可以使用切线拟合方法来近似函数的斜率。

具体做法是取一个足够靠近a的点x=a+h，然后利用该点和x=a处的函数值来计算斜率。

拟合的切线方程可以表示为：y=f(a)+f(a+h)-f(a)/h(x-a)。

3. 切线放缩与局部线性化：切线放缩方法是一种常用的近似方法，可以将函数在某一点附近的行为近似为一条直线。

切线放缩经常用于求函数的上下界、极值、渐近行为等问题。

将函数在点x=a处的切线方程表示为：y=f(a)+f'(a)(x-a)，即可得到切线放缩公式。

4. 切线放缩与泰勒展开：泰勒展开是将一个函数在某一点展开为无限项的幂级数，可以用来近似函数的行为。

切线放缩可以看作是泰勒展开的一种特殊情况，即取展开项为一阶导数。

切线放缩公式可以表示为：f(x)≈f(a)+f'(a)(x-a)，其中f'(a)为函数f(x)在点x=a处的导数。

5. 切线放缩与微分：微分是求函数在某一点的导数，也可以看作是切线的斜率。

切线放缩可以通过求导数来近似函数的行为。

利用导数来近似函数的最大值和最小值是切线放缩方法的一个重要应用。

综上所述，切线放缩公式是一个重要的数学工具，用于近似函数的行为。

它可以通过切线方程的一般形式、切线拟合、切线放缩与局部线性化、切线放缩与泰勒展开以及切线放缩与微分等方法来求得。

切线放缩方法在数学建模、优化问题以及物理学和工程学等领域都有广泛的应用。

补上一课 ,导函数的“隐零点”、e x ≥x ＋1、ln x ≤x －1及,“极值点偏移”问题1．利用导数解决函数问题常与函数单调性的判断有关，而函数的单调性与其导函数的零点有着紧密的联系，按导函数零点能否求精确解可以分为两类：一类是数值上能精确求解的，称之为“显零点”；另一类是能够判断其存在但无法直接表示的，称之为“隐零点”．对于隐零点问题，由于涉及灵活的代数变形、整体代换、构造函数、不等式应用等技巧，对学生综合能力的要求较高，成为考查的难点． 2．极值点“偏移”图示(1)(左右对称，无偏移，如二次函数；若f (x 1)＝f (x 2)，则x 1＋x 2＝2x 0)(2)(左陡右缓，极值点向左偏移；若f (x 1)＝f (x 2)，则x 1＋x 2＞2x 0)(3)(左缓右陡，极值点向右偏移；若f (x 1)＝f (x 2)，则x 1＋x 2＜2x 0)3．极值点偏移问题的结论不一定总是x 1＋x 2＞(＜)2x 0，也可能是x 1x 2＞(＜)x 20.题型一 函数最值中的“隐零点”【例1】 (2021·杭州市高级中学仿真考试)已知函数f (x )＝(x －a )e x (a ∈R )． (1)讨论f (x )的单调性；(2)当a ＝2时，设函数g (x )＝f (x )＋ln x －x －b ，b ∈Z ，若g (x )≤0对任意的x ∈⎝ ⎛⎭⎪⎫13，1恒成立，求b 的最小值．解 (1)由题意，函数f (x )＝(x －a )e x (a ∈R )， 可得f ′(x )＝(x －a ＋1)e x ， 当x ∈(－∞，a －1)时，f ′(x )<0； 当x ∈(a －1，＋∞)时，f ′(x )>0， 故函数f (x )在(－∞，a －1)上单调递减， 在(a －1，＋∞)上单调递增．(2)由函数g (x )＝f (x )＋ln x －x －b ＝(x －2)e x ＋ln x －x －b (b ∈Z )， 因为g (x )≤0对任意的x ∈⎝ ⎛⎭⎪⎫13，1恒成立．即b ≥(x －2)e x＋ln x －x 对任意的x ∈⎝ ⎛⎭⎪⎫13，1恒成立，令函数h (x )＝(x －2)e x ＋ln x －x ， 则h ′(x )＝(x －1)e x ＋1x －1＝(x －1)⎝ ⎛⎭⎪⎫e x －1x ，因为x ∈⎝ ⎛⎭⎪⎫13，1，所以x －1<0.再令函数t (x )＝e x －1x ，可得t ′(x )＝e x ＋1x 2>0， 所以函数t (x )单调递增．因为t ⎝ ⎛⎭⎪⎫12＝e 12－2<0，t (1)＝e －1>0，所以一定存在唯一的x 0∈⎝ ⎛⎭⎪⎫12，1，使得t (x 0)＝0，即e x 0＝1x 0，即x 0＝－ln x 0，所以h (x )在⎝ ⎛⎭⎪⎫13，x 0上单调递增，在(x 0，1)上单调递减，所以h (x )max ＝h (x 0)＝(x 0－2)e x 0＋ln x 0－x 0＝ 1－2⎝ ⎛⎭⎪⎫x 0＋1x 0∈(－4，－3)．因为b ∈Z ，所以b 的最小值为－3.感悟升华 解决函数最值中的隐零点问题关键在于灵活应用“隐零点”的等式进行代换使问题得以解决．【训练1】 设函数f (x )＝e 2x －a ln x (a 为大于零的常数)，已知f ′(x )＝0有唯一零点，求f (x )的最小值．解 f (x )的定义域为(0，＋∞)，f ′(x )＝2e 2x －ax (x ＞0)． 当a ＞0时，设u (x )＝e 2x ，v (x )＝－ax ，因为u (x )＝e 2x在(0，＋∞)上单调递增，v (x )＝－ax 在(0，＋∞)上单调递增，所以f ′(x )在(0，＋∞)上单调递增． 设f ′(x )在(0，＋∞)上的唯一零点为x 0，当x ∈(0，x 0)时，f ′(x )＜0； 当x ∈(x 0，＋∞)时，f ′(x )＞0.故f (x )在(0，x 0)上单调递减，在(x 0，＋∞)上单调递增， 所以当x ＝x 0时，f (x )取得最小值，最小值为f (x 0)． 由于2e 2x 0－ax 0＝0，所以f (x 0)＝a 2x 0＋2ax 0＋a ln 2a ≥2a ＋a ln 2a .故当a ＞0时，f (x )≥2a ＋a ln 2a .故f (x )的最小值为2a ＋a ln 2a .题型二 不等式证明中的“隐零点”【例2】 (2021·杭州统检)已知函数f (x )＝e x －a －ln (x ＋a )(x ≥0)，其中a >0. (1)若a ＝1，求证：f (x )>0；(2)若不等式f (x )≥2x ＋a ＋1－1－ln 2对x ≥0恒成立，试求a 的取值范围． (1)证明 由a ＝1，得f (x )＝e x －1－ln(x ＋1)，x ≥0，所以有f ′(x )＝e x －1－1x ＋1， 所以f ′(x )在[0，＋∞)上单调递增，且f ′(0)＝1e －1<0，f ′(1)＝12>0， 所以存在x 0∈(0，1)，使f ′(x 0)＝0， 所以当x ∈(0，x 0)时，f ′(x )<0， 当x ∈(x 0，＋∞)时，f ′(x )>0，所以f (x )min ＝f (x 0)＝e x 0－1－ln(x 0＋1)，(*) 且e x 0－1－1x 0＋1＝0，即e x 0－1＝1x 0＋1， 两边取对数，得ln(x 0＋1)＝1－x 0，代入(*)，有f(x)min＝f(x0)＝1x0＋1＋x0－1＝x20x0＋1>0恒成立，所以f(x)>0.(2)解由题意得e x－a－ln(x＋a)≥2x＋a＋1－1－ln 2对x≥0恒成立，①必要性将x＝1代入上述不等式，得e1－a－ln(1＋a)≥a＋3－1－ln 2，即ln(1＋a)＋a＋3－e1－a－1－ln 2≤0，令函数g(a)＝ln(1＋a)＋a＋3－e1－a－1－ln 2，易知g(a)在(0，＋∞)上单调递增，且g(1)＝0，所以0<a≤1.②下证当0<a≤1时，e x－a－ln(x＋a)≥2x＋a＋1－1－ln 2对x≥0恒成立，即证ln(x＋a)＋2x＋a＋1－e x－a≤1＋ln 2.因为0<a≤1，所以ln(x＋a)＋2x＋a＋1－e x－a≤ln(x＋1)＋2x＋2－e x－1. 设函数h(x)＝ln(x＋1)＋2x＋2－e x－1，则h′(x)＝1x＋1＋12x＋2－e x－1，显然h′(x)在[0，＋∞)上单调递减，且h′(1)＝0，所以h(x)在[0，1)上单调递增，在[1，＋∞)上单调递减，故h(x)≤h(1)＝1＋ln 2，不等式得证．由①和②可知0<a≤1，即a的取值范围为(0，1]．感悟升华把“隐零点”等式代入最值式是证明不等式的常用技巧．【训练2】(2021·杭州质检)设函数f(x)＝e x＋ax，a∈R.(1)若f(x)有两个零点，求a的取值范围；(2)若对任意的x∈[0，＋∞)均有2f(x)＋3≥x2＋a2，求a的取值范围．解(1)由题意得f′(x)＝e x＋a，当a≥0时，f′(x)>0，此时函数f(x)在R上单调递增，不符合题意；当a<0时，令f′(x)＝0，得x＝ln(－a)，函数f(x)在(－∞，ln(－a))上单调递减，在(ln(－a)，＋∞)上单调递增，则f(ln(－a))为f(x)的极小值，要使函数f(x)有两个零点，则f(ln(－a))<0，解得a<－e，所以a的取值范围为(－∞，－e)．(2)令g(x)＝2f(x)＋3－x2－a2＝2e x－(x－a)2＋3，x≥0，则g′(x)＝2(e x－x＋a)．设h(x)＝2(e x－x＋a)，则h′(x)＝2(e x－1)≥0.所以h(x)在[0，＋∞)上单调递增，且h(0)＝2(a＋1)．①当a＋1≥0，即a≥－1时，g′(x)≥0恒成立，即函数g(x)在[0，＋∞)上单调递增，所以g(0)＝5－a2≥0，解得－5≤a≤ 5.又a≥－1，所以－1≤a≤ 5.②当a＋1<0，即a<－1时，则存在x0>0，使h(x0)＝0且当x∈(0，x0)时，h(x)<0，即g′(x)<0，函数g(x)在(0，x0)上单调递减；当x∈(x0，＋∞)时，h(x)>0，即g′(x)>0，函数g(x)在(x0，＋∞)上单调递增，所以g(x)min＝g(x0)＝2e x0－(x0－a)2＋3.又h(x0)＝2(e x0－x0＋a)＝0，从而g(x)min＝g(x0)＝2e x0－x20＋2ax0－a2＋3＝2x0－2a－x20＋2ax0－a2＋3＝－x20＋2(a＋1)x0－(a＋3)(a－1)＝(－x0＋a＋3)(x0－a＋1)≥0，即a－1≤x0≤a＋3.由于x0是单调增函数h(x)＝2(e x－x＋a)在[0，＋∞)上的唯一零点，要使得a－1≤x0≤a＋3(a<－1)，则只需0≤x0≤a＋3，故只需保证g′(a＋3)＝2[e a＋3－2(a＋3)＋2a]≥0，即e a＋3≥3，故实数，ln 3－3≤a<－1.综上所述，a的取值范围为[ln 3－3，5]．题型三导函数中“二次函数”的“设而不求”技巧【例3】 (2018·全国Ⅰ卷)已知函数f (x )＝1x －x ＋a ln x . (1)讨论f (x )的单调性；(2)若f (x )存在两个极值点x 1，x 2，证明：f （x 1）－f （x 2）x 1－x 2<a －2.(1)解 f (x )的定义域为(0，＋∞)， f ′(x )＝－1x 2－1＋ax ＝－x 2－ax ＋1x 2.①若a ≤2，则f ′(x )≤0，当且仅当a ＝2，x ＝1时f ′(x )＝0， 所以f (x )在(0，＋∞)上单调递减． ②若a >2，令f ′(x )＝0得， x ＝a －a 2－42或x ＝a ＋a 2－42.当x ∈⎝ ⎛⎭⎪⎫0，a －a 2－42∪⎝ ⎛⎭⎪⎫a ＋a 2－42，＋∞时，f ′(x )<0； 当x ∈⎝ ⎛⎭⎪⎫a －a 2－42，a ＋a 2－42时，f ′(x )>0. 所以f (x )在⎝ ⎛⎭⎪⎫0，a －a 2－42，⎝ ⎛⎭⎪⎫a ＋a 2－42，＋∞上单调递减，在⎝ ⎛⎭⎪⎫a －a 2－42，a ＋a 2－42上单调递增． (2)证明 由(1)知，f (x )存在两个极值点时，当且仅当a >2. 由于f (x )的两个极值点x 1，x 2满足x 2－ax ＋1＝0， 所以x 1x 2＝1，不妨设x 1<x 2，则x 2>1.由于 f （x 1）－f （x 2）x 1－x 2＝－1x 1x 2－1＋a ln x 1－ln x 2x 1－x 2＝－2＋aln x 1－ln x 2x 1－x 2＝－2＋a －2ln x 21x 2－x 2，所以f （x 1）－f （x 2）x 1－x 2<a －2等价于1x 2－x 2＋2ln x 2<0.设函数g(x)＝1x－x＋2ln x，由(1)知，g(x)在(0，＋∞)上单调递减，又g(1)＝0，从而当x∈(1，＋∞)时，g(x)<0.所以1x2－x2＋2ln x2<0，即f（x1）－f（x2）x1－x2<a－2.【训练3】已知函数f(x)＝x2＋a ln(x＋2)，a∈R，存在两个极值点x1，x2，求f(x1)＋f(x2)的取值范围．解函数f(x)的定义域为(－2，＋∞)，且f′(x)＝2x＋ax＋2＝2x2＋4x＋ax＋2，由于f(x)有两个极值点，则二次函数g(x)＝2x2＋4x＋a在(－2，＋∞)上有两个相异实根x1，x2，由于g(x)的对称轴为x＝－1，由二次函数的图象可知，只需Δ＝16－8a>0且g(－2)＝a>0，即0<a<2. 考虑到x1，x2是方程2x2＋4x＋a＝0的两根．从而x1＋x2＝－2，x1x2＝a 2，从而f(x1)＋f(x2)＝x21＋a ln(x1＋2)＋x22＋a ln(x2＋2)＝(x1＋x2)2－2x1x2＋a ln[2(x1＋x2)＋x1x2＋4]＝4－a＋a ln a 2，其中0<a<2.令h(a)＝4－a＋a ln a2，a∈(0，2)，则h′(a)＝－1＋ln a2＋1＝lna2<0，从而h(a)在(0，2)上单调递减，又当x→0(x>0)，h(a)→4，a→2，h(a)→2，所以h(a)的值域为(2，4)．综上所述f(x1)＋f(x2)的取值范围是(2，4)．题型四不等式e x≥x＋1、ln x≤x－1的应用【例4】 (2020·七彩阳光联盟适考)函数f (x )＝ln(x ＋1)－ax ，g (x )＝1－e x . (1)讨论函数f (x )的单调性；(2)若f (x )≥g (x )在x ∈[0，＋∞)上恒成立，求实数a 的取值范围． 解 (1)函数f (x )的定义域为x ∈(－1，＋∞)， f ′(x )＝1x ＋1－a ＝－ax ＋1－a x ＋1. (ⅰ)当a ＝0时，f ′(x )>0，f (x )在(－1，＋∞)上单调递增；(ⅱ)当a ≠0时，令f ′(x )＝0得x ＝1－a a ＝1a －1，若a <0，则1a －1<－1，若a >0，则1a －1>－1.①当a <0时，f ′(x )＝1x ＋1－a >0，函数f (x )在(－1，＋∞)上单调递增；当a >0时，f ′(x )＝－a ⎝⎛⎭⎪⎫x －1－a a x ＋1，所以当x ∈⎝⎛⎭⎪⎫－1，1－a a 时，f ′(x )>0，f (x )单调递增， 当x ∈⎝ ⎛⎭⎪⎫1－a a ，＋∞时，f ′(x )<0，f (x )单调递减，综上可得，当a ≤0时，f (x )在(－1，＋∞)上单调递增； 当a >0时，f (x )在⎝⎛⎭⎪⎫－1，1－a a 上单调递增， 在⎝ ⎛⎭⎪⎫1－a a ，＋∞上单调递减． (2)设函数h (x )＝f (x )－g (x )＝ln(x ＋1)＋e x －ax －1，x ≥0， 则h ′(x )＝1x ＋1＋e x －a ， 当a ≤2时，由e x ≥x ＋1得 h ′(x )＝1x ＋1＋e x －a ≥1x ＋1＋x ＋1－a ≥0， 于是，h (x )在[0，＋∞)上单调递增， 所以h (x )≥h (0)＝0恒成立，符合题意； 当a >2时 ，由于x ≥0，h (0)＝0， 令函数m (x )＝h ′(x )，则m′(x)＝－1（x＋1）2＋e x(x≥0)．所以m′(x)≥0，故h′(x)在[0，＋∞)上单调递增，而h′(0)＝2－a<0.则存在一个x0>0，使得h′(x0)＝0，所以当x∈[0，x0)时，h(x)单调递减，故h(x0)<h(0)＝0，不符合题意．综上，实数a的取值范围为(－∞，2]．感悟升华在函数、导函数不等式中，对于出现e x，ln x时，要注意应用结论e x≥x ＋1，x－1≥ln x，e x≥e x.【训练4】(2020·山东卷)已知函数f(x)＝a e x－1－ln x＋ln a.(1)当a＝e时，求曲线y＝f(x)在点(1，f(1))处的切线与两坐标轴围成的三角形的面积；(2)若f(x)≥1，求a的取值范围．解f(x)的定义域为(0，＋∞)，f′(x)＝a e x－1－1 x.(1)当a＝e时，f(x)＝e x－ln x＋1，f′(1)＝e－1，曲线y＝f(x)在点(1，f(1))处的切线方程为y－(e＋1)＝(e－1)(x－1)，即y＝(e－1)x＋2.直线y＝(e－1)x＋2在x轴、y轴上的截距分别为－2e－1，2.因此所求三角形的面积为2e－1.(2)当0<a<1时，f(1)＝a＋ln a<1.当a＝1时，f(x)＝e x－1－ln x，f′(x)＝e x－1－1 x.当x∈(0，1)时，f′(x)<0；当x∈(1，＋∞)时，f′(x)>0. 所以当x＝1时，f(x)取得最小值，最小值为f(1)＝1，从而f(x)≥1.当a>1时，f(x)＝a e x－1－ln x＋ln a>e x－1－ln x≥1.综上，a的取值范围是[1，＋∞)．题型五 “极值点”的偏移【例5】 已知函数f (x )＝x e －x . (1)求函数f (x )的单调区间和极值；(2)已知函数g (x )的图象与f (x )的图象关于直线x ＝1对称，证明：当x ＞1时，f (x )＞g (x )；(3)如果x 1≠x 2，且f (x 1)＝f (x 2)，证明：x 1＋x 2＞2.(1)解 f ′(x )＝e －x (1－x )，得f (x )在(－∞，1)上递增，在(1，＋∞)上递减，f (x )有极大值f (1)＝1e ，无极小值．(2)证明 由g (x )的图象与f (x )的图象关于直线x ＝1对称，得g (x )的解析式为y ＝f (2－x )，构造辅助函数F (x )＝f (x )－g (x )＝f (x )－f (2－x )，x ∈(1，＋∞)， 求导得F ′(x )＝f ′(x )－[f (2－x )]′＝e －x (1－x )＋e x －2(x －1)＝(x －1)(e x －2－e －x )，当x ＞1时，x －1＞0，e x －2－e －x ＞0，则F ′(x )＞0，得F (x )在(1，＋∞)上单增，有F (x )＞F (1)＝0，即f (x )＞g (x )．(3)证明 由f (x 1)＝f (x 2)，结合f (x )的单调性可设x 1＜1＜x 2，将x 2代入(2)中不等式得f (x 2)＞f (2－x 2)，又f (x 1)＝f (x 2)，故f (x 1)＞f (2－x 2)，又x 1＜1，2－x 2＜1，f (x )在(－∞，1)上单增，故x 1＞2－x 2，x 1＋x 2＞2.感悟升华 用对称化构造的方法解决极值点偏移问题分为以下三步：(1)求导，获得f (x )的单调性，极值情况，作出f (x )的图象，由f (x 1)＝f (x 2)得x 1，x 2的取值范围(数形结合)；(2)构造辅助函数，对结论x 1＋x 2＞(＜)2x 0，构造F (x )＝f (x )－f (2x 0－x )；对结论x 1x 2＞(＜)x 20，构造F (x )＝f (x )－f ⎝ ⎛⎭⎪⎫x 20x ，求导，限定范围(x 1或x 2的范围)，判定符号，获得不等式；(3)代入x 1(或x 2)，利用f (x 1)＝f (x 2)及f (x )的单调性证明最终结论．【训练6】 已知函数f (x )＝(x －2)e x ＋a (x －1)2有两个零点(a ＞0)．设x 1，x 2是f (x )的两个零点，证明：x 1＋x 2<2.证明 由f ′(x )＝(x －1)e x ＋2a (x －1)＝(x －1)(e x ＋2a )，知f (x )在(－∞，1)上递减，在(1，＋∞)上递增，f (1)＝－e ，由f (x 1)＝f (x 2)＝0，可设x 1＜1＜x 2.构造辅助函数F (x )＝f (x )－f (2－x )，求导得F ′(x )＝f ′(x )－[f (2－x )]′＝(x －1)(e x ＋2a )－(x －1)(e 2－x ＋2a )＝(x －1)(e x －e 2－x )，当x ＜1时，x －1＜0，e x －e 2－x ＜0，则F ′(x )＞0，得F (x )在(－∞，1)上单增，又F (1)＝0，故F (x )＜0(x ＜1)，即f (x )＜f (2－x )(x ＜1)．将x 1代入上述不等式中，得f (x 1)＝f (x 2)＜f (2－x 1)，又x 2＞1，2－x 1＞1，f (x )在(1，＋∞)递增，故x 2＜2－x 1，x 1＋x 2＜2.1．证明：e x －ln x >2.证明 设f (x )＝e x －ln x (x >0)，则f ′(x )＝e x－1x ，令φ(x )＝e x －1x ，则φ′(x )＝e x ＋1x 2>0在(0，＋∞)恒成立， 所以φ(x )在(0，＋∞)单调递增，即f ′(x )＝e x －1x 在(0，＋∞)上是增函数，又f ′(1)＝e －1>0，f ′⎝ ⎛⎭⎪⎫12＝e －2<0， ∴f ′(x )＝e x －1x 在⎝ ⎛⎭⎪⎫12，1内有唯一的零点． 不妨设f ′(x 0)＝0，则e x 0＝1x 0，从而x 0＝ln 1x 0＝－ln x 0， 所以当x >x 0时，f ′(x )>0；当0<x <x 0时，f ′(x )<0.∴f (x )＝e x －ln x 在x ＝x 0处有极小值，也是最小值．∴f (x )min ＝f (x 0)＝e x 0－ln x 0＝1x 0＋x 0>2，x 0∈⎝ ⎛⎭⎪⎫12，1. 故e x －ln x >2.2．已知函数f (x )＝(x －1)e x －ax 的图象在x ＝0处的切线方程是x ＋y ＋b ＝0.(1)求a ，b 的值；(2)求证函数f (x )有唯一的极值点x 0，且f (x 0)>－32.(1)解 因为f ′(x )＝x e x －a ，由f ′(0)＝－1得a ＝1，又当x ＝0时，f (x )＝－1，所以切线方程为y －(－1)＝－1(x －0)，即x ＋y ＋1＝0，所以b ＝1.(2)证明 令g (x )＝f ′(x )＝x e x －1，则g ′(x )＝(x ＋1)e x ，所以当x <－1时，g (x )单调递减，且此时g (x )<0，则g (x )在(－∞，－1)内无零点；当x ≥－1时，g (x )单调递增，且g (－1)<0，g (1)＝e －1>0，所以g (x )＝0有唯一解x 0，f (x )有唯一的极值点x 0.由x 0e x 0＝1⇒e x 0＝1x 0， f (x 0)＝x 0－1x 0－x 0＝1－⎝ ⎛⎭⎪⎫1x 0＋x 0， 又g ⎝ ⎛⎭⎪⎫12＝e 2－1<0， g (1)＝e －1>0⇒12<x 0<1⇒2<1x 0＋x 0<52， 所以f (x 0)>－32.3．已知f (x )＝ax ＋x ln x (a ∈R )，y ＝f (x )在点(1，f (1))处的切线的斜率为2.若2f (x )－(k ＋1)x ＋k >0(k ∈Z )对任意x >1都成立，求整数k 的最大值．解 由题设知f ′(x )＝a ＋1＋ln x ，由f ′(1)＝2，解得a ＝1，所以f (x )＝x ＋x ln x .当x >1时，不等式2f (x )－(k ＋1)x ＋k >0(k ∈Z )化为k <x ＋2x ln x x －1，记g (x )＝x ＋2x ln x x －1(x >1)，则g ′(x )＝2x －2ln x －3（x －1）2， 再设h (x )＝2x －2ln x －3，则h ′(x )＝2（x －1）x >0， 所以h (x )在(1，＋∞)上单调递增，又h (2)＝1－2ln 2<0，h ⎝ ⎛⎭⎪⎫52＝2⎝ ⎛⎭⎪⎫1－ln 52>0， 故h (x )在⎝ ⎛⎭⎪⎫2，52上存在唯一零点x 0， 使h (x 0)＝2x 0－2ln x 0－3＝0，且当1<x <x 0时，g ′(x )<0；当x >x 0时，g ′(x )>0.即g (x )在(1，x 0)单调递减，在(x 0，＋∞)单调递增，所以g (x )min ＝g (x 0)＝x 0＋2x 0ln x 0x 0－1， 由2x 0－2ln x 0－3＝0得2ln x 0＝2x 0－3，则g (x )min ＝x 0＋x 0（2x 0－3）x 0－1＝2x 0∈(4，5)， 又k <x ＋2x ln x x －1恒成立， 故整数k 的最大值为4.4．已知函数f (x )＝e x －a .(1)若函数f (x )的图象与直线l ：y ＝x －1相切，求a 的值；(2)若f (x )－ln x >0恒成立，求整数a 的最大值．解 (1)f ′(x )＝e x ，因为函数f (x )的图象与直线y ＝x －1相切，所以令f ′(x )＝1，即e x ＝1，得x ＝0，∴切点坐标为(0，－1)，则f (0)＝1－a ＝－1，∴a ＝2.(2)先证明e x ≥x ＋1，设F (x )＝e x －x －1，则F ′(x )＝e x －1，令F ′(x )＝0，则x ＝0，当x ∈(0，＋∞)时，F ′(x )>0；当x ∈(－∞，0)时，F ′(x )<0.所以F (x )在(0，＋∞)上单调递增，在(－∞，0)上单调递减，所以F (x )min ＝F (0)＝0，即F (x )≥0恒成立．∴e x ≥x ＋1，从而e x －2≥x －1(x ＝0时取等号)．以ln x 代换x 得ln x ≤x －1(当x ＝1时，等号成立)，所以e x －2>ln x .当a ≤2时，ln x <e x －2≤e x －a ，则当a ≤2时，f (x )－ln x >0恒成立．当a ≥3时，存在x ，使e x －a <ln x ，即e x －a >ln x 不恒成立．综上，整数a 的最大值为2.5．已知函数f (x )＝x ln x －x ，两相异正实数x 1，x 2满足f (x 1)＝f (x 2)．求证：x 1＋x 2＞2.证明 f ′(x )＝ln x ，当x ∈(0，1)时，f (x )单减，当x ＞1时，f (x )单增，且f (1)＝－1，如图所示，不妨设x 1＜1＜x 2，要证x 1＋x 2＞2，即证x 2＞2－x 1，只需要证f (2－x 1)＜f (x 2)，又f (x 1)＝f (x 2)，所以只需证f (2－x 1)＜f (x 1)，设g (x )＝f (x )－f (2－x )(x ∈(0，1))，则g ′(x )＝f ′(x )－[f (2－x )]′＝ln x ＋ln(2－x )，0＜x ＜1，符号不易判断，再设h (x )＝ln x ＋ln(2－x )，0＜x ＜1，则h ′(x )＝1x －12－x ＝2－2x x （2－x ）＞0，∴h (x )在(0，1)上单增，∴h (x )＜h (1)＝0，∴g (x )在(0，1)上单减，∴g (x )＞g (1)＝0， ∴f (x )－f (2－x )＞0；0＜x ＜1，∴f (x 1)＞f (2－x 1)成立，∴x 1＋x 2＞2.6．(2017·全国Ⅲ卷)已知函数f (x )＝x －1－a ln x .(1)若f (x )≥0，求a 的值；(2)设m 为整数，且对于任意正整数n ，⎝ ⎛⎭⎪⎫1＋12⎝ ⎛⎭⎪⎫1＋122·…·⎝ ⎛⎭⎪⎫1＋12n <m ，求m 的最小值．解 (1)f (x )的定义域为(0，＋∞)，①若a ≤0，因为f ⎝ ⎛⎭⎪⎫12＝－12＋a ln 2<0，所以不满足题意． ②若a >0，由f ′(x )＝1－a x ＝x －a x 知，当x ∈(0，a )时，f ′(x )<0；当x ∈(a ，＋∞)时，f ′(x )>0；所以f (x )在(0，a )单调递减，在(a ，＋∞)单调递增，故x ＝a 是f (x )在(0，＋∞)的唯一最小值点．因为f (1)＝0，所以当且仅当a ＝1时，f (x )≥0，故a ＝1.(2)由(1)知当x ∈(1，＋∞)时，x －1－ln x >0，令x ＝1＋12n ，得ln ⎝ ⎛⎭⎪⎫1＋12n <12n. 从而ln ⎝ ⎛⎭⎪⎫1＋12＋ln ⎝ ⎛⎭⎪⎫1＋122＋…＋ln ⎝ ⎛⎭⎪⎫1＋12n <12＋122＋…＋12n ＝1－12n <1. 故⎝ ⎛⎭⎪⎫1＋12⎝ ⎛⎭⎪⎫1＋122·…·⎝ ⎛⎭⎪⎫1＋12n <e ， 又⎝ ⎛⎭⎪⎫1＋12⎝ ⎛⎭⎪⎫1＋122⎝ ⎛⎭⎪⎫1＋123＝13564>2， 从而m 的最小正整数是m ＝3.7．(2021·台州评估测试)已知函数f (x )＝e x －x 2，g (x )＝ax .(1)求证：存在唯一的实数a ，使得直线y ＝g (x )与曲线y ＝f (x )相切；(2)若a ∈[1，2]，x ∈[0，2]，求证：|f (x )－g (x )|≤e 2－6.(注：e ＝2.718 28…为自然对数的底数)证明 (1)由f ′(x )＝e x －2x 知，函数f (x )在点(t ，f (t ))处的切线方程为y －(e t －t 2)＝(e t －2t )(x －t )，当该直线为y ＝ax 时，可得⎩⎨⎧a ＝e t －2t ，e t －t 2＝t （e t －2t ），所以(t －1)e t －t 2＝0，所以t >1.令函数h (t )＝(t －1)e t －t 2，则当t >1时，h ′(t )＝t (e t －2)>0，所以函数h (t )在(1，＋∞)上单调递增，而h (1)＝－1<0，h (2)＝e 2－4>0，所以存在唯一的实数t 0∈(1，2)，使得h (t 0)＝0，相应的a ＝e t －2t 也是唯一的，即存在唯一的实数a ，使得直线y ＝g (x )与曲线y ＝f (x )相切．(2)要证|f (x )－g (x )|≤e 2－6，即证6－e 2≤e x －x 2－ax ≤e 2－6.令函数F (a )＝e x －x 2－ax ，对于确定的x ，F (a )是一次函数，只要证明⎩⎨⎧6－e 2≤F （1）≤e 2－6，6－e 2≤F （2）≤e 2－6，注意到对于同一x ∈[0，2]，F (1)≥F (2)，所以只要证明⎩⎨⎧F （1）≤e 2－6，①F （2）≥6－e 2.②先证明①：记函数G (x )＝F (1)＝e x －x 2－x ，则G ′(x )＝e x －2x －1，令y ＝e x －2x －1，因为y ′＝e x －2，令y ′>0⇒x >ln 2，由此可知G ′(x )在[0，ln 2]上单调递减，在[ln 2，2]上单调递增．又因为G ′(0)＝0，G ′(ln 2)＝e ln 2－2ln 2－1<0，G ′(2)＝e 2－5>0，所以在[ln 2，2]上存在唯一实数x 0，使得G ′(x 0)＝0，故在[0，x 0]上G (x )单调递减，在[x 0，2]上G (x )单调递增．所以G (x )max ＝max{G (0)，G (2)}＝e 2－6，即F (1)≤e 2－6，①得证；再证明②：记函数H (x )＝F (2)＝e x －x 2－2x ，当x ∈[0，1]时，利用不等式e x ≥x ＋1得H (x )≥(x ＋1)－x 2－2x ＝－x 2－x ＋1≥1－1－1＝－1>6－e 2；当x ∈[1，2]时，利用不等式e x≥x 22＋x ＋1(x ≥0)得e·e x －1≥e·⎣⎢⎡⎦⎥⎤（x －1）22＋（x －1）＋1＝e 2x 2＋e 2. 于是H (x )≥⎝ ⎛⎭⎪⎫e 2x 2＋e 2＋(－2x －x 2)＝⎝ ⎛⎭⎪⎫e 2－1x 2－2x ＋e 2. 其中二次函数φ(x )＝⎝ ⎛⎭⎪⎫e 2－1x 2－2x ＋e 2开口向上，对称轴为x ＝2e －2>2， 所以当x ∈[1，2]时，φ(x )的最小值为φ(2)＝4⎝ ⎛⎭⎪⎫e 2－1－4＋e 2＝5e 2－8， 所以H (x )≥φ(x )≥φ(2)>6－e 2.综上，不等式①②均成立，所以当x ∈[0，2]时，对任意的a ∈[1，2]，总有|f(x)－g(x)|≤e2－6.。

所有让你背结论的放缩法都是耍流氓，导数处理之切线放缩
要画图
作者：霍焰（湖北省沙市中学）
近些年，放缩法不断出现在各省的高考压轴导数题中，但是有些题目的标准答案的放缩显得突兀，让人不能把握为什么要这样放缩，以至于教师的讲解变成了无用功，学生听得懂但是碰到新题也无从下手．在此，笔者希望通过几个高考题来抓取此类放缩问题的处理方向。

01本题第（Ⅱ）问参考答案所给的两种证法放缩技巧性都很强，这里笔者试图用最基本的转化化归，及一个常用的对数不等关系式lnx＜x-1来解决问题．需要注意的是这里并不想突出结论的记忆，这里应该注意的是依靠图象法进行思考的过程．有了使用图形的观念，我们的放缩将会有一定的目的性0203如果在数学考试中学生只知道使用老师罗列的结论解决问题，那其实不叫学好了数学，上面的结论并不重要，重要的是使用图形解决问题的观念本题第（Ⅱ）问的参考答案所给的方法给人的感觉是，明知道内幕假装写过程，根本无法解释为什么会这样做，所以这里依旧从图象的角度去寻找思路．转化化归与数形结合是高中阶段的重要思想方法，我们可以通过将陌生函数转化为熟悉函数，然后通过熟悉函数的图象对问题进行观察思考，找到解题的路径．即使图象法不能直接使用与解题，但
至少它可以帮我们进行思考．。