函数的凹凸性
- 格式：ppt
- 大小：699.00 KB
- 文档页数：3
下载文档原格式
合集下载
《函数曲线的凹凸性》课件
《函数曲线的凹凸性》 ppt课件
CONTENTS 目录
• 引言 • 函数曲线的凹凸性判定 • 函数曲线的凹凸性性质 • 函数曲线的凹凸性与导数的关系 • 函数曲线的凹凸性与几何意义 • 总结与展望
CHAPTER 01
引言
凹凸性的定义
凹函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) geq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凹函数。
函数曲线的凹凸性可能会随着自变量x 的变化而发生变化。
凸函数曲线
表示函数图像呈上凸的几何形状，即 任意两点之间的连线位于曲线上方。
几何形状的凹凸性实例
下凹函数曲线
$f(x) = x^2$，$f(x) = sin x$
上凸函数曲线
$f(x) = log x$，$f(x) = e^x$
几何形状的凹凸性与生活中的应用
02
二次函数是典型的凹函数和凸函数，其图像为抛物 线。
03
指数函数和幂函数在其定义域内是凹函数，对数函 数在其定义域内是凸函数。
CHAPTER 04
函数曲线的凹凸性与导数的关系
导数与凹凸性的关系
01
导数大于0的区间内，函数曲线为 凹；
02
导数小于0的区间内，函数曲线为 凸。
导数在判断凹凸性中的应用
凸函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) leq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凸函数。
CONTENTS 目录
• 引言 • 函数曲线的凹凸性判定 • 函数曲线的凹凸性性质 • 函数曲线的凹凸性与导数的关系 • 函数曲线的凹凸性与几何意义 • 总结与展望
CHAPTER 01
引言
凹凸性的定义
凹函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) geq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凹函数。
函数曲线的凹凸性可能会随着自变量x 的变化而发生变化。
凸函数曲线
表示函数图像呈上凸的几何形状，即 任意两点之间的连线位于曲线上方。
几何形状的凹凸性实例
下凹函数曲线
$f(x) = x^2$，$f(x) = sin x$
上凸函数曲线
$f(x) = log x$，$f(x) = e^x$
几何形状的凹凸性与生活中的应用
02
二次函数是典型的凹函数和凸函数，其图像为抛物 线。
03
指数函数和幂函数在其定义域内是凹函数，对数函 数在其定义域内是凸函数。
CHAPTER 04
函数曲线的凹凸性与导数的关系
导数与凹凸性的关系
01
导数大于0的区间内，函数曲线为 凹；
02
导数小于0的区间内，函数曲线为 凸。
导数在判断凹凸性中的应用
凸函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) leq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凸函数。
函数凹凸的定义
02 函数凹凸的几何意义
凹函数的几何意义
凹函数图像呈下凹状，即对于函数图 像上的任意两点A和B，如果A、B两 点连线的中点始终位于A、B连线的下 方，则该函数为凹函数。
在几何意义上，凹函数具有一个明显 的特征，即函数图像上任意两点的连 线的斜率始终小于或等于该点处的函 数导数。
凸函数的几何意义
通过分析函数的凹凸性，我们可以确定函数的拐点，从而更好地理解函数 的性质，为求解最优化问题提供指导。
在求解无约束最优化问题时，可以利用函数凹凸性选择合适的算法，如梯 度下降法、牛顿法等，以提高求解效率。
在经济学中的应用
函数凹凸性在经济学中也有 广泛应用，它可以帮助我们 理解经济现象和预测经济行
为。
函数凹凸的定义
目录
• 函数凹凸的基本概念 • 函数凹凸的几何意义 • 函数凹凸的判定方法 • 函数凹凸的应用 • 函数凹凸的反例 • 函数凹凸的扩展知识
01 函数凹凸的基本概念
凹函数
01
凹函数是指函数图形在任意两点 之间总是位于这两点连线的下方， 即对于定义域内的任意x1和x2， 都有 f((x1+x2)/2)≥f(x1)+f(x2)/2。
03
在计算机科学中，函数凹凸性可以帮助我们设计更有效的算法和数据 结构，如动态规划、图算法等。
04
在生物学中，函数凹凸性可以帮助我们理解生物系统的复杂性和行为， 如生态学、生物化学反应等。
05 函数凹凸的反例
凹函数的反例
总结词
凹函数的反例是指函数图像呈现下凹形状的反例。
详细描述
凹函数的反例通常是指那些在一定区间内，函数值随着自变量的增加而减少的函数。例如，二次函数 $f(x) = x^2$在区间$(-infty, 0)$内是一个凹函数的反例，因为在这个区间内，函数值随着$x$的增加 而减少。
函数的凹凸性ppt课件
函数的凹凸性
一、曲线的凹凸性与拐点
1
一、曲线的凹凸性与拐点
如图，观察抛物线 y x2 , y x ，它们
在区间[0，1]上都是单调增加的，但弯曲的方向
不一样。
y
这说明，在研究函数的图形时，
仅知道他们的单调性是不够的， 1
还需要考察曲线的弯曲方向及 扭转弯曲方向的点。
o1
x
2
二、凹凸与拐点的定义 y
② f (x1 x2 ) f (x1 ) f (x2 ) ；
③ f (x1 ) f (x2 ) 0; x1 x2
④ f ( x1 x2 ) f (x1 ) f (x2 ) .
2
2
当 f (x) lg x 时，上述结论中正确结论的序号
是
.
9
10
【详解】
对于①②可以用 f (x) lg x
y log2 x 在 0 x 1内为凸函数。所以答案为 B。
点评:只要能作出这四个初等函数的草图,马上根据函数 的凹凸性可直接作结论.
8
典例 2.（05 北京理工科 13）．对于函数 f (x) 定义域中
任意的 x1 , x2 (x1 x2 ) ，有如下结论：
① f (x1 x2 ) f (x1 ) f (x2 ) ；
的研究函数的一个概念，是用来研究函数图象的变化趋 势的。
【高考联接】在高考中常借助函数的凹凸性来考查基
本初等函数的图象及性质，这一知识点常渗透在与函数 的图象与性质的选择填空题中。经常与高中所学的函数、 三角、不等式知识相结合。此类问题的常规处理思路有 数形结合法、导数分析法、增量分析法、估猜法等。
y (1)x a
• (0,1)
y ax (a 1)
16
一、曲线的凹凸性与拐点
1
一、曲线的凹凸性与拐点
如图，观察抛物线 y x2 , y x ，它们
在区间[0，1]上都是单调增加的，但弯曲的方向
不一样。
y
这说明，在研究函数的图形时，
仅知道他们的单调性是不够的， 1
还需要考察曲线的弯曲方向及 扭转弯曲方向的点。
o1
x
2
二、凹凸与拐点的定义 y
② f (x1 x2 ) f (x1 ) f (x2 ) ；
③ f (x1 ) f (x2 ) 0; x1 x2
④ f ( x1 x2 ) f (x1 ) f (x2 ) .
2
2
当 f (x) lg x 时，上述结论中正确结论的序号
是
.
9
10
【详解】
对于①②可以用 f (x) lg x
y log2 x 在 0 x 1内为凸函数。所以答案为 B。
点评:只要能作出这四个初等函数的草图,马上根据函数 的凹凸性可直接作结论.
8
典例 2.（05 北京理工科 13）．对于函数 f (x) 定义域中
任意的 x1 , x2 (x1 x2 ) ，有如下结论：
① f (x1 x2 ) f (x1 ) f (x2 ) ；
的研究函数的一个概念，是用来研究函数图象的变化趋 势的。
【高考联接】在高考中常借助函数的凹凸性来考查基
本初等函数的图象及性质，这一知识点常渗透在与函数 的图象与性质的选择填空题中。经常与高中所学的函数、 三角、不等式知识相结合。此类问题的常规处理思路有 数形结合法、导数分析法、增量分析法、估猜法等。
y (1)x a
• (0,1)
y ax (a 1)
16
函数的凹凸性
yloagxa
3、幂函数
yx y
y x2
1
(是常)数
yx y x
(1,1)
o1
x
y 1 x
6、双曲函数
由 ex, ex 构成.
ycosxh
双曲 si正 n xh ex 弦 ex
2 y 1ex
D:(, ), 奇函数.
（2） 如果x 0,1 时 f (x) 1，试求实数a的范围。
解析：（1）对任意的
x, 1
x 2
R,
a
0
，
f (x ) 1
f (x ) 2
2
f
(
x 1
x 2
)
＝
2
ax2 1
x 1
ax2 2
x 2
2a(
x 1
2
x 2
)2
x 1
2
x 2
A
o
x
问题: 如何用准确的数学语言描述曲线的凹凸性?
y
yf(x)
y yf(x)
o x1
x2 x
图形上任意弧段（的中点）
位于所张弦的下方。
o x1
x2 x
图形上任意弧段（的中点）
位于所张弦的上方。
二、曲线的凹凸性与拐点
y
C
问题:如何研究曲线的弯曲方向?
B
y
yf(x) f(x1) f(x2)
2
解析:答案为 B。要使 f ( x1 x2 ) f (x1 ) f (x2 ) 恒成
2
2
立，由函数值的定义及函数图象即需要函数在 0 x 1
《函数的凹凸性》课件
凸函数的性质
凸函数图像呈上凸状，即对于函数图像上的任意两点A(x1, y1)和B(x2, y2)，当x1 < x2时，y1 < y2。
凸函数的导数在定义域内小于0，即f''(x) < 0。
凸函数具有局部最大值，即对于任意x0属于定义域，存在一个邻域使得 该邻域内所有点的函数值都小于或等于f(x0)。
在物理学中，凹凸性可以用于描述物 体的弹性、光学性质等。
在经济学中，凹凸性可以用于描述商 品的需求和供给关系，以及价格和产 量的变化关系。
在计算机科学中，凹凸性可以用于图 像处理、机器学习等领域。
02
函数的凹凸性判定
判定方法一：二阶导数法
总结词
举例说明
二阶导数法是判断函数凹凸性的常用 方法之一，通过计算函数的二阶导数 并分析其符号来判断函数的凹凸性。
05
实际应用案例
金融领域的应用
金融数据分析
函数的凹凸性在金融数据分析中有着广泛的应用，如股票价格、收益率等金融时间序列数 据的分析，通过识别数据的凹凸性，可以预测未来的价格走势和风险评估。
投资组合优化
在投资组合优化中，凹凸性可用于确定最优投资组合，通过最小化投资组合的风险或最大 化预期收益，实现资产的有效配置。
判定方法三：几何意义法
总结词
几何意义法是通过观察函数图像 ቤተ መጻሕፍቲ ባይዱ几何形状来判断函数的凹凸性
。
详细描述
如果一个函数的图像是一条向下 凸出的弧形线，则该函数是凹的 ；如果图像是一条向上凸起的弧
形线，则函数是凸的。
举例说明
以函数$f(x) = x^4 - x^2$为例 ，通过绘制该函数的图像可以观 察到，该函数在$x < 0$时图像 向下凸出，因此函数$f(x) = x^4
函数的凹凸性与拐点
5
课程思政
课程思政：奥运精神 播放视频《谷爱凌自由式滑雪夺冠》
播放视频
曲线的凹凸性正如滑雪运动员在跳台上滑过的优美曲线。北京2022 年冬奥会自由式滑雪女子大跳台决赛，中国选手谷爱凌在最后一跳中 首次跳出了1620的超高难度，夺得金牌！ 赛后，谷爱凌表示，采取超 高难度动作，想要挑战自己，并不是为了赢对手，展示自己的体育精 神。谷爱凌希望自己的精神，让大家能够体会体育精神，做到打破和 突破，成就最好的自己。我们在学习和生活中也应该向她学习不屈不 挠的奥运精神，突破自己，展现自我。
凹的
99
2凹凸性的定理 练习2 求函数y x4的凹凸性
1100
谢谢观看
2凹凸性的定理
定理 设函数 y f (x) 在 (a,b)内有二阶导数。 那么（1）若在 (a,b) 内 f (x) 0，则曲线在 (a,b) 内上凹。 （2）若在 (a,b) 内 f (x) 0，则曲线在 (a,b)内下凹。
7
2凹凸性的定理
拐点：如果点P的两侧，函数的凹凸性不一样，那么 这样的点P叫做函数的拐点。
8
2凹凸性的定理
例2 求曲线 y 3x4 4x3 1的拐点及凹、凸的区间
解： D : (,)
y 12x3 令y 0,
12x2 , 得 x1
0,
y x2
36x(x 2. 3
2). 3
x
(,0)
0
(0, 23)
2 3
(
2 3
,)
f (x)
00Biblioteka 拐点拐点f (x)
凹的
0,1 凸的
（2，11） 3 27
曲线的凹凸性与拐点
数学教研室
目录
CONTENT
课程思政
课程思政：奥运精神 播放视频《谷爱凌自由式滑雪夺冠》
播放视频
曲线的凹凸性正如滑雪运动员在跳台上滑过的优美曲线。北京2022 年冬奥会自由式滑雪女子大跳台决赛，中国选手谷爱凌在最后一跳中 首次跳出了1620的超高难度，夺得金牌！ 赛后，谷爱凌表示，采取超 高难度动作，想要挑战自己，并不是为了赢对手，展示自己的体育精 神。谷爱凌希望自己的精神，让大家能够体会体育精神，做到打破和 突破，成就最好的自己。我们在学习和生活中也应该向她学习不屈不 挠的奥运精神，突破自己，展现自我。
凹的
99
2凹凸性的定理 练习2 求函数y x4的凹凸性
1100
谢谢观看
2凹凸性的定理
定理 设函数 y f (x) 在 (a,b)内有二阶导数。 那么（1）若在 (a,b) 内 f (x) 0，则曲线在 (a,b) 内上凹。 （2）若在 (a,b) 内 f (x) 0，则曲线在 (a,b)内下凹。
7
2凹凸性的定理
拐点：如果点P的两侧，函数的凹凸性不一样，那么 这样的点P叫做函数的拐点。
8
2凹凸性的定理
例2 求曲线 y 3x4 4x3 1的拐点及凹、凸的区间
解： D : (,)
y 12x3 令y 0,
12x2 , 得 x1
0,
y x2
36x(x 2. 3
2). 3
x
(,0)
0
(0, 23)
2 3
(
2 3
,)
f (x)
00Biblioteka 拐点拐点f (x)
凹的
0,1 凸的
（2，11） 3 27
曲线的凹凸性与拐点
数学教研室
目录
CONTENT
函数的凹凸性,极值
y
y f (x) B
y y f (x)
B
A
oa
bx
f ( x) 递增 y 0
A oa
f ( x) 递减
bx y 0
4
四、曲线凹凸的判定
定理2 如果 f ( x) 在 [a,b] 上连续,在 (a,b) 内具有
二阶导数 ,若在 (a,b)内 (1) f ( x) 0,则 f ( x) 在 [a,b] 上的图形是凹的; (2) f ( x) 0,则 f ( x) 在 [a,b] 上的图形是凸的.
f (x1)
f
(
x2
)
2
f
(
x1
2
x2)
1 2!
(
x2
2
x1
)
2
[
f
(1)
f (2 )]
当 f (x) 0时,
f
( x1) 2
f
(x2 )
f (x1 x2 ),
2
说明 (1) 成立; (2)
7
例2 判别曲线 y 1 的凹凸性. x
解 函数的定义域为 ( , 0) U (0, ) .
故 f (t) et 所对应的曲线在 ( , ) 内是凹的 . x, y ( , ) , 由曲线凹性的定义, 有
1
(e x
e
y
)
e
x y 2
,
(x y) .
2
9
y
y x3
O
在 (, 0)上 , y x3是凸的,
此时 y 0 .
在 (0, )上 ,
x
y x3 是凹的,
此时 y 0 .
f ( x) 0 ( x x0 )
14
函数的凹凸性与拐点
xfln (x x) y f ln ( yy ) (x x y )y x y 即 f( ln( ) ) 2 2 22 2
得证.
15
不等式证明的方法：
1、拉格朗日中定理；
2、函数的单调性、极值； 3、函数的凹凸性；
16
作业：
P 3 134
17
爱是什么？ 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来，停在枝上，望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道：“你爱这稻谷吗？” “爱。” “为什么？” “它驱赶我的饥饿。” 鸟儿啄完稻谷，轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗？”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答：“现在我爱那一湾泉水，我有点渴了。” 精灵摘下一片树叶，里面盛了一汪泉水。 鸟儿喝完泉水，准备振翅飞去。 “请再回答我一个问题，”精灵伸出指尖，鸟儿停在上面。 “你要去做什么更重要的事吗？我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷，去看那朵风信子。” “为什么？它能驱赶你的饥饿？” “不能。” “它能滋润你的干渴？” “不能。”爱是什么？ 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来，停在枝上，望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道：“你爱这稻谷吗？” “爱。” “为什么？” “它驱赶我的饥饿。” 鸟儿啄完稻谷，轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗？”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答：“现在我爱那一湾泉水，我有点渴了。” 精灵摘下一片树叶，里面盛了一汪泉水。 鸟儿喝完泉水，准备振翅飞去。 “请再回答我一个问题，”精灵伸出指尖，鸟儿停在上面。 “你要去做什么更重要的事吗？我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷，去看那朵风信子。” “为什么？它能驱赶你的饥饿？” “不能。” “它能滋润你的干渴？” “不能。”
得证.
15
不等式证明的方法：
1、拉格朗日中定理；
2、函数的单调性、极值； 3、函数的凹凸性；
16
作业：
P 3 134
17
爱是什么？ 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来，停在枝上，望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道：“你爱这稻谷吗？” “爱。” “为什么？” “它驱赶我的饥饿。” 鸟儿啄完稻谷，轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗？”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答：“现在我爱那一湾泉水，我有点渴了。” 精灵摘下一片树叶，里面盛了一汪泉水。 鸟儿喝完泉水，准备振翅飞去。 “请再回答我一个问题，”精灵伸出指尖，鸟儿停在上面。 “你要去做什么更重要的事吗？我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷，去看那朵风信子。” “为什么？它能驱赶你的饥饿？” “不能。” “它能滋润你的干渴？” “不能。”爱是什么？ 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来，停在枝上，望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道：“你爱这稻谷吗？” “爱。” “为什么？” “它驱赶我的饥饿。” 鸟儿啄完稻谷，轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗？”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答：“现在我爱那一湾泉水，我有点渴了。” 精灵摘下一片树叶，里面盛了一汪泉水。 鸟儿喝完泉水，准备振翅飞去。 “请再回答我一个问题，”精灵伸出指尖，鸟儿停在上面。 “你要去做什么更重要的事吗？我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷，去看那朵风信子。” “为什么？它能驱赶你的饥饿？” “不能。” “它能滋润你的干渴？” “不能。”
《函数凹凸性》课件
几何意义
在函数图像上，凸函数表现为图像位于其连接直线的上方。
凹凸函数的几何意义
凹函数的几何意义
在凹函数的图像上，任意两点之间的线段都位于这两点之间函数的曲线下方。这 表明，对于凹函数，中点的函数值总是大于或等于两端点连线上中点的函数值。
凸函数的几何意义
在凸函数的图像上，任意两点之间的线段都位于这两点之间函数的曲线上方。这 表明，对于凸函数，中点的函数值总是小于或等于两端点连线上中点的函数值。
几何意义
在函数图像上，凹函数表现为图像位于其连接直线的下方。
凸函数的定义
凸函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1, x_2$（ $x_1 < x_2$）都有$f(x_1) + f(x_2) < 2f[(x_1 + x_2)/2]$， 则称$f(x)$在区间$I$上是凸函数。Βιβλιοθήκη 4凹凸性在优化问题中的应用
利用凹凸性求解优化问题
01
确定函数的凹凸性
首先需要判断函数的凹凸性，可以通过求二阶导数或观察函数图像来进
行判断。
02 03
利用凹凸性寻找极值点
在确定了函数的凹凸性之后，可以利用凹凸性寻找函数的极值点。在凹 函数中，极值点出现在二阶导数为0的点；在凸函数中，极值点出现在 边界点或一阶导数为0的点。
有$f(x_1) + f(x_2) < 2fleft(frac{x_1 + x_2}{2}right)$，则称$f(x)$在区间$I$上是凸函数。
二次导数法
总结词
通过判断一阶导数的正负来判断函数 凹凸性的常用方法
详细描述
如果函数$f(x)$的二阶导数$f''(x) > 0$，则函数$f(x)$为凹函数；如果二 阶导数$f''(x) < 0$，则函数$f(x)$为 凸函数。这种方法适用于一阶导数容 易计算或形式较为简单的函数。
在函数图像上，凸函数表现为图像位于其连接直线的上方。
凹凸函数的几何意义
凹函数的几何意义
在凹函数的图像上，任意两点之间的线段都位于这两点之间函数的曲线下方。这 表明，对于凹函数，中点的函数值总是大于或等于两端点连线上中点的函数值。
凸函数的几何意义
在凸函数的图像上，任意两点之间的线段都位于这两点之间函数的曲线上方。这 表明，对于凸函数，中点的函数值总是小于或等于两端点连线上中点的函数值。
几何意义
在函数图像上，凹函数表现为图像位于其连接直线的下方。
凸函数的定义
凸函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1, x_2$（ $x_1 < x_2$）都有$f(x_1) + f(x_2) < 2f[(x_1 + x_2)/2]$， 则称$f(x)$在区间$I$上是凸函数。Βιβλιοθήκη 4凹凸性在优化问题中的应用
利用凹凸性求解优化问题
01
确定函数的凹凸性
首先需要判断函数的凹凸性，可以通过求二阶导数或观察函数图像来进
行判断。
02 03
利用凹凸性寻找极值点
在确定了函数的凹凸性之后，可以利用凹凸性寻找函数的极值点。在凹 函数中，极值点出现在二阶导数为0的点；在凸函数中，极值点出现在 边界点或一阶导数为0的点。
有$f(x_1) + f(x_2) < 2fleft(frac{x_1 + x_2}{2}right)$，则称$f(x)$在区间$I$上是凸函数。
二次导数法
总结词
通过判断一阶导数的正负来判断函数 凹凸性的常用方法
详细描述
如果函数$f(x)$的二阶导数$f''(x) > 0$，则函数$f(x)$为凹函数；如果二 阶导数$f''(x) < 0$，则函数$f(x)$为 凸函数。这种方法适用于一阶导数容 易计算或形式较为简单的函数。
函数凹凸性的几个应用
1 n
(ln
a1
+ln
a2
+… +ln
an )≤l n
a1 +a2
+… +an n
,
化简得
n
a1 a2
…an
≤
1 n
(a 1
+a2
+… +an).
注 :利用函数凸性证明不等式的关键在于 构造或
引进我们所需的辅助函 数 , 使条 件和结 论 、已知 与未 知建立联系.
2. 求最值 从不等式的证明中我们可以看到 , 如果不 等式的
=
1 2
|an
-1Βιβλιοθήκη |2|an - 1| 22|an - 1|
=
2 2
,
又 0≤〈 an - 1 , an〉 ≤π, ∴an - 1 与 an 的夹角为 π4 .
(3)a1
=( x1
,
y1),
a2
=
1 2
(
x1
-
y1
,
x 1 +y1) ,
a3
=
1 4
(
-
2
y1
, 2 x1)=
1 2
(-
y1
,
x1) ,
凸函数.
2.
f(
x1
+x2 2
)
≥
f(
x1)+ 2
f(
x2)
,
则称
f( x)是 上
凸函数.
判定定理 :若函 数 f( x)在[ a, b] 连续 且在(a, b)
内具有一阶和二阶导数 , 则
1. 若在(a , b)内 f″( x) <0, 则 f(x)在[ a, b] 是上
函数凹凸性
2) 根据拐点的定义, 可得拐点的判别法如下:
若曲线
或不存在,
但 f (x) 在 x0 两侧异号, 则点(x0 , f (x0 )) 是曲线
的一个拐点.
求拐点的步骤见教材P162.
机动 目录 上页 下页 返回 结束
例4. 求曲线
的上（下）凸区间及拐点.
解: 1) 求 y
y 12x3 12x2,
36x(x 32)
机动 目录 上页 下页 返回 结束
(2) 若恒有
则称
图形是上凸的; 或称f (x)为I上的上凸函数。
弦在弧的下方；切线在曲线的上方。
下凸也称为凸，上凸也称为凹。 y
o
x1 x1 x2 x2 x
2
机动 目录 上页 下页 返回 结束
等价定义：
定义1´：设函数 在区间 I 上连续 ,
(1) 若恒有
则称
f (1) f (0) f ( ) (0 1)
机动 目录 上页 下页 返回 结束
作业
P168 1（3，6）；2 ; 3； 5（1，3） 6（3，4）；7（2）
第七节 目录 上页 下页 返回 结束
例如, 双曲线
L PN
o
x
有渐近线
x y0
y
ab
但抛物线
无渐近线 .
ox
机动 目录 上页 下页 返回 结束
1. 水平与铅直渐近线
若
则曲线
有水平渐近线 y b.
(或x )
若
则曲线
有垂直渐近线 x x0 .
(或x x0 )
例1. 求曲线
的渐近线 .
解: lim ( 1 2) 2
2
x x 1
证明：
令
函数的凸凹性及其应用
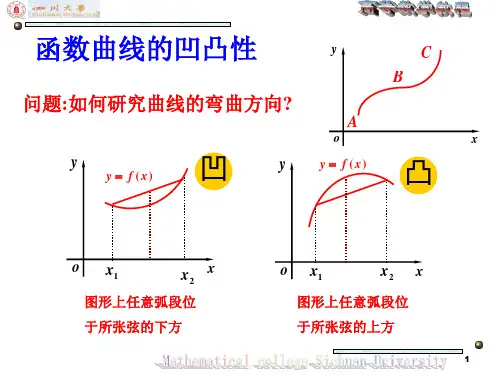
函数的凸凹性及其应用定义:函数的凸凹性 定义：如果函数()f x 对其定义域中任意的1x ,2x 都有[])()(21)2(2121x f x f x x f +≤+成立，则称)(x f 是下凸（凸）函数(如图1所示)，当且仅当21x x =时等号成立．如果函数()f x 对其定义域中任意的1x ,2x 都有[])()(21)2(2121x f x f x x f +≥+成立，则称)(x f 是上凸（凹）函数(如图2所示)，当且仅当21x x =时等号成立．定理1 （Jensen 不等式）若函数()f x 在区间I 是上凸函数，则有不等式：)()()()(22112211n n n n x f q x f q x f q x q x q x q f +++≥+++ ;若函数()f x 在区间I 是下凸函数，则有不等式：)()()()(22112211n n n n x f q x f q x f q x q x q x q f +++≤+++ ,其中n i q I x i i,,2,1,0, =>∈；121=+++n q q q ．定理2 若)(x f 是下凸函数，则其对应定义域中的任意n 个点n x x x ,,21恒有：[])()()(1)(2121n n x f x f x f nn x x x f +++≤+++ ;类似地，对于上凸函数有：[])()()(1)(2121n n x f x f x f nn x x x f +++≥+++ ,当且仅当n x x x === 21时等号成立．定理3：设函数)(x f 在开区间I 上存在二阶导数：(1)若对任意I x ∈，有0)(>''x f ，则)(x f 在I 上为下凸函数; (2)若对任意I x ∈，有0)(<''x f ，则)(x f 在I 上为上凸函数．下面对于一些常用的的函数的凹凸性作一个探讨．（1）对数函数:)10(log ≠>=a a x y a 且若10<<a ，则为下凸函数；若1>a，则为上凸函数． （2）指数函数)1,0(≠>=a a a y x且为下凸函数．（3）三角函数sin (0,)(,23cos (,)(,2222tan (,0)(022y x x x y x x x y x x x πππππππππ=∈∈=∈-∈=∈-∈，是上凸函数;）是下凸函数;，是上凸函数;）是下凸函数;，是上凸函数;，）是下凸函数.（4）二次函数:)0(2≠++=a c bx ax y若0>a ，则为下凸函数；若0<a ，则为上凸函数．（5）反比例函数:)0(≠=k xky当0>k 时: 若)0,(-∞∈x ，则为上凸函数；若),0(+∞∈x ，则为下凸函数． 当0<k 时: 若)0,(-∞∈x ，则为下凸函数；若),0(+∞∈x ，则为上凸函数．（6）双勾函数:)0,0(>>+=b a xbax y当)0,(-∞∈x 时，为上凸函数；当),0(+∞∈x 时，为下凸函数．T1 设()y f x =是(),a b 上的严格凸函数，则对于(),a b 内的任意n 个点12,,,n x x x ，都有()()()()12121n n x x x f f x f x f x n n+++⎛⎫≤+++ ⎪⎝⎭ ，当且仅当12n x x x === 时等号成立。
求函数的凹凸区间及拐点的步骤
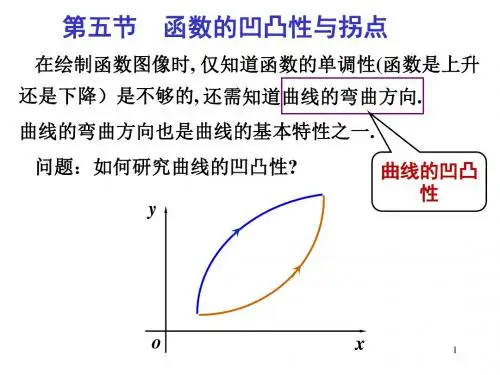
求函数的凹凸区间及拐点的步骤一、概念解析在数学中，我们经常会遇到求函数的凹凸区间及拐点的问题。
这涉及到了函数的二阶导数，以及函数图像的变化规律。
下面我将按照从简到繁的方式，逐步探讨这一主题。
1. 凹凸性的概念我们需要了解什么是函数的凹凸性。
对于函数f(x)，若在区间I上满足f''(x)>0（f''(x)表示f(x)的二阶导数），则称函数f(x)在I上是凹的；若在区间I上满足f''(x)<0，则称函数f(x)在I上是凸的。
2. 拐点的概念另外，拐点指的是函数图像上的一个特殊点，该点对应的二阶导数f''(x)发生变号的点。
二、步骤探究接下来，我们将讨论求函数的凹凸区间及拐点的具体步骤。
我将结合具体的例子来说明每一步的操作方法，以便你能更深入地理解。
1. 求导数我们需要求出函数f(x)的一阶和二阶导数，分别记为f'(x)和f''(x)。
这一步是求凹凸区间及拐点的基础。
2. 解方程f''(x)=0在区间I上，我们需要解方程f''(x)=0，找出f(x)的二阶导数为0的点。
这些点就是函数可能存在拐点的位置。
3. 列出数表我们需要列出f''(x)的变号区间，并通过数表的形式进行展示。
在这一步，我们可以通过选取区间内的特定点，代入f''(x)的值，来判断函数的凹凸性。
4. 确定凹凸区间及拐点根据数表中f''(x)的正负情况，我们可以确定函数f(x)的凹凸区间，并找出拐点的具体位置。
这样，我们就完成了求函数的凹凸区间及拐点的步骤。
三、总结回顾通过以上步骤，我们可以比较清晰地了解了如何求函数的凹凸区间及拐点。
在实际应用中，我们可以通过这些步骤，快速、准确地分析函数的凹凸性质，从而更好地理解函数的图像特征。
个人观点：求函数的凹凸区间及拐点是数学中的重要问题，它不仅有着重要的理论意义，也在实际问题的解决中发挥着重要作用。
导数与函数的凹凸性
导数与函数的凹凸性导数是微积分中的一个基本概念，用于描述函数的变化率。
而函数的凹凸性则是研究函数曲线的形状和性质的重要内容。
导数与函数的凹凸性之间存在着密切的关联。
一、导数的定义与性质导数的定义是描述函数在某一点处的变化率。
对于函数y=f(x)，其在点x处的导数定义为：f'(x) = lim (h->0)[f(x+h)-f(x)]/h导数可以用来刻画函数曲线在某一点处的切线斜率。
如果导数值为正，说明函数在该点递增；若导数值为负，说明函数在该点递减；若导数值为零，则说明函数在该点达到了极值。
导数还有着一些基本性质：1. 导数的线性性质：设函数f(x)和g(x)在某一点的导数分别为f'(x)和g'(x)，常数k，则有：(kf(x))' = kf'(x)(f(x) + g(x))' = f'(x) + g'(x)2. 导数与常数的关系：常数的导数为零，即(k)' = 03. 导数的乘积法则：设函数u(x)和v(x)在某一点的导数分别为u'(x)和v'(x)，则有：(u(x)v(x))' = u'(x)v(x) + u(x)v'(x)二、函数的凹凸性定义函数的凹凸性是描述函数曲线的弯曲程度的概念。
若函数图像上的任意两点的连线段都位于函数曲线的上方，那么这个函数是凹函数；若函数图像上的任意两点的连线段都位于函数曲线的下方，那么这个函数是凸函数。
三、函数凹凸性与导数之间的关系1. 凹凸性与导数一阶导数的关系对于函数f(x)，若其在区间[a,b]上二阶可导且二阶导数f''(x)恒大于零，则f(x)在[a,b]上是凹函数；若f''(x)恒小于零，则f(x)在[a,b]上是凸函数。
2. 凹凸性与导数二阶导数的关系如果函数f(x)在某一点x处的二阶导数f''(x)存在且大于零，则该点为f(x)的一个极小值点，即f(x)在该点处是凹函数；如果f''(x)存在且小于零，则该点为f(x)的一个极大值点，即f(x)在该点处是凸函数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解析:答案为 B。要使 f ( x1 x2 ) f (x1 ) f (x2 ) 恒成
2
2
立，由函数值的定义及函数图象即需要函数在 0 x 1
内为凸函数。而 y 2x , y x2 在 0 x 1内为凹函数，
y cos 2x 在 0 x 1 内 先 凸 后 凹 函 数 。 只 有
直接验证即可②满足题意 对于③④如右图所示：
对于 f (x) lg x 图象上任意不同
两点 A(x1, f (x1))B(x2, f (x2 ))
k AB
f (x1) f (x2 ) 0 x1 x2
显然成
立（可
以用
f '(x) 1 0(x 0) ）故③正确 x ln10
再有 AB 中点 C（ x1 x2 , f (x1) f (x2 ) ) 过 C
1 x
1，
x2 x x 2 4
当 1 1时， (1 1)2 1 取得最大值 2， (1 1)2 1 取得最小值0
x
x2 4
x2 4
2 a 0 结合 a 0，a [2,0)。
指数函数、对数函数、幂函数等基本初等函数的凹凸性。
1、指数函数 y a x (a 0, a 1) y e x
② f (x1 x2 ) f (x1 ) f (x2 ) ；
③ f (x1 ) f (x2 ) 0; x1 x2
④ f ( x1 x2 ) f (x1 ) f (x2 ) .
2
2
当 f (x) lg x 时，上述结论中正确结论的序号
是
.
【详解】
对于①②可以用 f (x) lg x
函数的凹凸性
一、曲线的凹凸性与拐点
一、曲线的凹凸性与拐点
如图，观察抛物线 y x2 , y x ，它们
在区间[0，1]上都是单调增加的，但弯曲的方向
不一样。
y
这说明，在研究函数的图形时，
仅知道他们的单调性是不够的， 1
还需要考察曲线的弯曲方向及 扭转弯曲方向的点。
o1
x
二、凹凸与拐点的定义 y
解析：（1）对任意的
x, 1
x 2
R,
a
0
，
f (x ) 1
f (x ) 2
2
f
(
x 1
x 2
)
＝
2
ax2 1
x 1
ax2 2
x 2
2a(
x 1
2
x 2
)2
x 1
2
x 2
ax2 1
ax2 2
1 2
a(x2 1
x2 2
1
＝
2
a(x 1
x )2 2
0 ，
f
x (1
2
x 2)
1f
2
(x ) 1
的研究函数的一个概念，是用来研究函数图象的变化趋 势的。
【高考联接】在高考中常借助函数的凹凸性来考查基
本初等函数的图象及性质，这一知识点常渗透在与函数 的图象与性质的选择填空题中。经常与高中所学的函数、 三角、不等式知识相结合。此类问题的常规处理思路有 数形结合法、导数分析法、增量分析法、估猜法等。
C
B
定义: 若曲线段向上（下）弯曲，
则称之为凹（凸）的。
A
o
x
问题: 如何用准确的数学语言描述曲线的凹凸性?
y
y f (x)
y
y f (x)
o x1
x2 x
图形上任意弧段（的中点）
位于所张弦的下方。
o x1
Байду номын сангаас
x2 x
图形上任意弧段（的中点）
位于所张弦的上方。
二、曲线的凹凸性与拐点
y
C
问题:如何研究曲线的弯曲方向?
典例 1. （05 湖北卷）
在 y 2 x , y log2 x, y x2 , y cos 2x 这 四 个 函 数
中 ， 当 0 x1 x2 1 时 ， 使
f ( x1 x2 ) f (x1 ) f (x2 ) 恒成立的函数的个数
2
2
是（ B ）
A．0 B． 1 C．2 D．3
y (1)x a
• (0,1)
y ax (a 1)
2、对数函数 y loga x (a 0,a 1) y ln x
y log a x
(1,0)
•
(a 1)
y log 1 x
a
3、幂函数
f
(
x 1
x 2
)
1
f (x ) f (x ) 则称函数 f (x) 是 R 上的凹函数，已知二次函
2
2
1
2
数 f (x) ax2 x(a R 且 a 0)，
（1） 求证：当 a 0 时函数 f (x) 是凹函数；
（2） 如果 x 0,1 时 f (x) 1，试求实数 a 的范围。
x1 x1 x2 x2
x
2
图形上任意弧段位 于所张弦的上方
二、曲线的凹凸与拐点
定义 . 设函数 在区间 I 上连续 ,
(1) 若恒有
图形是凹的; (2) 若恒有
图形是凸的 .
yyy
连续曲线上有切线的凹凸分界点
称为拐点 .
ooo
则称 则称
xx11
xx11xx22 22
xx22
xxx
【知识背景】函数的凹凸性是高等数学的数学分析中
y log2 x 在 0 x 1内为凸函数。所以答案为 B。
点评:只要能作出这四个初等函数的草图,马上根据函数 的凹凸性可直接作结论.
典例 2.（05 北京理工科 13）．对于函数 f (x) 定义域中
任意的 x1 , x2 (x1 x2 ) ，有如下结论：
① f (x1 x2 ) f (x1 ) f (x2 ) ；
B
y
y f (x) f ( x1) f ( x2 )
2
f ( x1 )
f ( x1 x2 ) 2
f (x2 )
o
x x1
x1 x2 2
x2
图形上任意弧段位
于所张弦的下方
A
o
x
y
f ( x1 x2 ) 2
y f (x)
f ( x1 ) f ( x2 ) 2
f ( x1 )
f (x2 )
o
f
(x ) 故函数 2
f
(x) 是
凹函数。
（2）由 f (x) 1 1 f (x) 1 1 ax2 x 1 ①
ax2 x 1
当
x
0时， a R ，当
x (0,1]时①即 ax2
x
恒成立
1
a 即
a
1
x2 1
1
x 1
(1 1)2 x2
(1 1)2 1
1 4
恒成立，当
x (0,1]时
2
2
作
DC
x
轴交
f
(x)
于
D（
x1
2
x2
,
yD )
D
在
f (x)
上
有
：
yD
f
( x1
2
x2
)
yC
f (x1) f (x2 ) 故④不正确 2
点评:本题主要考查了 f (x) lg x 函数运算性质以及直
线斜率应用,题目较综合.判断④不正确也可直接利 用函数图象的上凸性作结论.
定 义 在 R 上 的 函 数 f (x) 满 足 ： 如 果 对 任 意 x , x R 都 有 12