当前位置：文档之家 › 函数的凹凸性与作图

函数的凹凸性与作图

  • 格式：ppt
  • 大小：2.46 MB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

高数上凹向、拐点、作图

高数上凹向、拐点、作图
解
2 y 36 x 24 x 36 x x 3 2 2 0 3 得 x 0 , x 令y 0 1 2 · · 3 x 0时， y 0; 在区间（－∞，0]内曲线是凹的。 2 2 0 x 时， y 0 ; 在区间[0， ]上曲线是凸的。 3 3 2 x 时， y 0. 在区间[ 2 ，＋∞）内曲线是凹的。 3 3 2 11 0 , 1、 , 是拐点. 3 27
x2 2
得到曲线上的两个点 （0 ,
1 2
）、（ 1，
1
另外f 2
1 , 2 2 e

1
加辅助点 ( 2 ,
2e 1 ). 2 2 e
）

1
2
注：本例特点 （1）利用函数的奇偶性； （2）补充点（0 ，y ( 0 ) ），（2 ，y ( 2 ) ）； （3）有水平渐近线。
f ' ( x1 ) f ' ( x2 ) f ' ( x3 ),
f x 递减
f x 0
f x 0
在有些教材中，凹的（曲线）又叫“上凹”，凸的又叫“下凹”。
连续曲线上，不同凹向曲线段的分界点，称为曲线的拐点。 注意：拐点是曲线上的点，应由两个坐标表示：（ x0 , f ( x0 ) ）. 前面讲过的极值点，是取得极值时自变量的值，记 为 x = xi。 两者不同。 2、曲线凹向的判定 P106定理3.8 函数y = f ( x ) 在闭区间 [ a , b ] 上连续,在开区间内二阶可导， 则当 仍可用“雨水法则” f ”( x ) > 0 时，曲线上凹（凹）； 帮助记忆 f ”( x ) < 0 时，曲线下凹（凸）。

《函数曲线的凹凸性》课件

《函数曲线的凹凸性》课件
《函数曲线的凹凸性》 ppt课件
CONTENTS 目录
• 引言 • 函数曲线的凹凸性判定 • 函数曲线的凹凸性性质 • 函数曲线的凹凸性与导数的关系 • 函数曲线的凹凸性与几何意义 • 总结与展望
CHAPTER 01
引言
凹凸性的定义
凹函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) geq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凹函数。
函数曲线的凹凸性可能会随着自变量x 的变化而发生变化。
凸函数曲线
表示函数图像呈上凸的几何形状，即 任意两点之间的连线位于曲线上方。
几何形状的凹凸性实例
下凹函数曲线
$f(x) = x^2$，$f(x) = sin x$
上凸函数曲线
$f(x) = log x$，$f(x) = e^x$
几何形状的凹凸性与生活中的应用
02
二次函数是典型的凹函数和凸函数，其图像为抛物 线。
03
指数函数和幂函数在其定义域内是凹函数，对数函 数在其定义域内是凸函数。
CHAPTER 04
函数曲线的凹凸性与导数的关系
导数与凹凸性的关系
01
导数大于0的区间内，函数曲线为 凹；
02
导数小于0的区间内，函数曲线为 凸。
导数在判断凹凸性中的应用
凸函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) leq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凸函数。

高等数学课件3-7凹凸性

高等数学课件3-7凹凸性

凹凸性研究的重要成果和突破
添加项标题
19世纪初，法国数学家拉格朗日提出了函数的凹凸性概念，为 研究函数的性质提供了新的工具。
添加项标题
19世纪末，德国数学家魏尔斯特拉斯提出了函数的极值定理， 为研究函数的凹凸性提供了理论基础。
添加项标题
20世纪初，英国数学家哈代和波兰数学家莱维提出了函数的凹 凸性判别法，为研究函数的凹凸性提供了新的方法。
化证明过程
举例：利用凸 函数的性质， 可以证明不等 式f(x) > g(x)
凹凸性在优化问题中的应用
凸优化问题：求解凸函数最小值 凹优化问题：求解凹函数最大值 凸优化算法：梯度下降法、牛顿法等
凹优化算法：梯度上升法、牛顿法等
凸优化与凹优化的区别：凸优化问题有 唯一解，凹优化问题可能有多个解
凸优化与凹优化的应用：在机器学习、 图像处理、信号处理等领域有广泛应用
,
汇报人：
目录
凹函数和凸函数的定义
凹函数：对于任意x1,x2∈D， f(x1)+f(x2)≥2f((x1+x2)/2)
凹函数和凸函数的区别在于不等号 的方向不同
添加标题
添加标题
凸函数：对于任意x1,x2∈D， f(x1)+f(x2)≤2f((x1+x2)/2)
添加标题Βιβλιοθήκη 添加标题凹函数和凸函数的定义是判断函数 凹凸性的基础
研究前景：凹凸性研究在许多领域都有广泛的应用前景，如优化问题、图像处理、机 器人控制等
汇报人：
凹凸性的几何意义
凸性：函数在某点处的切线斜 率大于等于该点处的函数值
凹性：函数在某点处的切线斜 率小于等于该点处的函数值
凸性函数：函数图像在定义域 内任意两点之间是凸的

3.5凹凸性与函数图形描绘PPT课件

3.5凹凸性与函数图形描绘PPT课件
3.5 曲线的凹凸性与函数作图
• 一.曲线的凹凸性及拐点 • 二.函数图形的描绘
一、凹凸性及拐点
y
y f (x) B
凹
A
oa
bx
y f (x)
y
B
凸
A oa
bx
1.定义 设函数f(x)在区间I上除端点外都可导，
x0为I的任一内点，若对 x I( x x0 )，恒有
f (x) f (x0 )(x x0 ) f (x0 ) ( f (x) f (x0)(x x0) f (x0)) 则称函数曲线 y 在f (区x)间I上是(向上)凹 的. (凸)
5 补充点，如与坐标轴的 交点、间断点、始点、 终点.
6 光滑连接各点，绘出函 数图形。
例5
作函数 ( x)
1
x2
e2
的图形.
2
解 1 [0,), （偶函数, 图形关于y轴对称）
2 ( x)
令 ( x) 0,
x
x2
e 2,
2
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
得驻点 x 0,
令 ( x) 0,
得 x 1, x 1.
3°列表确定函数增减区间,凹凸区间及极值点 与拐点:
x
( x) ( x) ( x)
0 (0,1) 1 (1,)
0
0
1 2
拐点
(1, 1 ) 2e
4 lim ( x) lim
1
x2
e 2 0,
得水平渐近线
y 0.
x
x 2
( x)
1
x2
e2
2
写在最后

函数的凹凸与曲线的凸向、拐点和渐近线、函数作图

函数的凹凸与曲线的凸向、拐点和渐近线、函数作图
x y x ln x y ln y 。 从而 ( x y )ln 2
10
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
二、曲线的拐点
1． 定义：连续曲线上曲线向上凸与向下凸的分界点 称为曲线的拐点。
2£ Õ ã Ä Ð ¨· ® ¹ µ µ Ŷ¨
与极值点判断类似 ， f ( x ) 0 的点和 f ( x ) 不存在 的点，是拐点横坐标 的可疑点。
2(1 x 2 ) 2x （2） y 2 ， y 2 ， 2 ( x 1) x 1
（3）令 y 0 ，得 x 1 ， x 1 。
x y
曲线 y
Hale Waihona Puke (, 1)-1 0拐点 (-1，ln2)
(-1， 1) +
1 0
拐点 (1，ln2)
(1, )
例如： f ( x ) x 4 ， f ( x ) 12 x 2 ，有 f (0) 0 ，但 （0，0）不是拐点。
12
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
例 2．求曲线 y ln( x 1) 的凸向和拐点。
2
解： （1）函数的定义域为 (,) ；
则称函数 f 为区间 I 上的凸函数； 若总有 f ( p1 x1 p2 x2 ) p1 f ( x1 ) p1 f ( x2 ) ，则称函数 f 为区间 I 上的凹函数。
3
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
y
y f ( x)
y
A
o a x1
D B
C
x
x2 b x
2
x2 x x x1 令 p1 , p2 ， 则 p1 0 ， p2 0 且 p1 p2 1 ， x2 x1 x2 x1

高等数学第七节 曲线的凹凸及拐点 函数作图

高等数学第七节 曲线的凹凸及拐点 函数作图
的凹凸与拐点，了解函数作图的基本方法.
2、本节重点、难点 重点：曲线凹凸的判定. 难点：曲线凹凸的判定.
3、本节知识结构
曲 线 的函 凹数 凸作 及图 拐 点
曲线的凹凸 及拐点
函数作图
凹凸、拐点的定义 定理（凹凸性定理）
水平渐近线、 垂直渐近线 作图步骤
当 x0时 ,y0,曲线是 ; 凸的
当 x0时 ,y0,曲线是 , 凹的
所( 以 ,0 )为凸 ,(0, 区 )为 间 凹 . 区间
因x为 0时不在,所 定以 义曲 域.线 内无
二、函数作图 作函数的,图 大形 致应遵循以:下步骤 (1)初步 :如 研 讨 究 论 ,对定 称 ,周 义 性 期 ,等 域 ;性 等
地掌握其形状.
图321,函 y f ( x 数 ) 的 A 段 B y g ( x 与 ) 的 C 段 ,它 D
都是,但 递 A段 B 增是 的凸 ,C段 D 的是 递凹 ,增的
因此还需要判断曲的线凹的凸 .
y
B
D
图321
yf(x)
A
C
o
yg(x)
x
从图 322中可以,看到 当x增大,曲 时线上对应点 斜处 率的 递 (左 切 减 图 )线 , 则曲线是凸的;
f ( x) s i nx 的渐近线？ x
思考题解答
limsinx0 x x
y 0 是 其 图 象 的 渐 近 线 .
y sin x x
limsinx1 x0 x
x 0 不 是 其 图 象 的 渐 近 线 .
三、小结
1、本节基本要求 理解曲线凹凸与拐点的概念，会求较简单曲线
当x增大,曲 时线上对应点 斜处 率的 递 (右 切 增 图 )线 ,

4.4 函数的凹凸性与函数的作图

4.4 函数的凹凸性与函数的作图
称 设曲线 y f ( x) ，如果 lim f ( x) c ,则 x y f ( x) yc 直线 为曲线 的水平渐近线.
2.铅垂渐近线
如果曲线 y f ( x) 在点 x0 间断，且
lim f ( x) ，则称直线 x x0 为曲线 x y f ( x) 的铅垂渐近线．
y 6 6 x 6(1 x)
y
x 0
6 0 ，所以 x 0 为极小值点，
f (0) 0 为极小值；y Nhomakorabeax2
6 0 ，所以 x 2为极大值点，
f (2) 4 为极大值.
(5)令 y 0 ，得 x 1．在 x 1 的左 侧有 y 0 ，在 x 1的右侧有 y 0 ， 而 f (1) 2 ，所以 (1,2)是拐点．
例 解
证明函数 y ln x 的图像是处处下凹(凹)的
函数y ln x的定义域为(0, )
1 y x 1 y 2 0 x
x (0, )
故曲线在整个定义域内是下凹(凸)的
定义4.3 曲线上凹与下凹的分界点称为 曲线的拐点. 求拐点的一般步骤： ①求函数的二阶导数 f ( x) ； ②令 f ( x) 0，解出全部根，并求出所 有二阶导数不存在的点； ③对步骤②求出的每一个点，检查其左、 右邻近的 f ( x) 的符号，如果异号则该点为曲 线的拐点；如果同号则该点不是曲线的拐点．
y
y f ( x)
A
B
y
y f ( x)
B
A
o
a
b
x
o
a
f ( x ) 递增
y 0
f ( x ) 递减
b x y 0

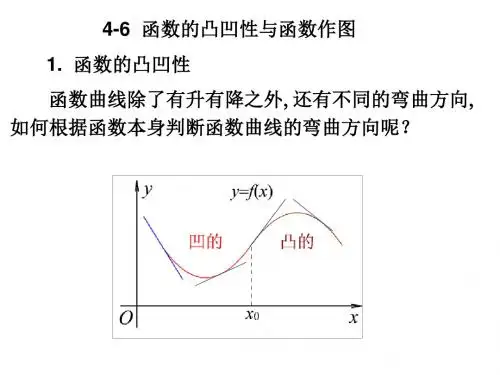
4-6函数的凸凹性与函数作图 (2)

4-6函数的凸凹性与函数作图 (2)
4-6 函数的凸凹性与函数作图 1. 函数的凸凹性 函数曲线除了有升有降之外, 还有不同的弯曲方向, 如何根据函数本身判断函数曲线的弯曲方向呢？
函数的凸(向上凸)凹(向下凸)性定义
设 y f x在 a,b 上可导, 若对于每一点 x0 a,b ,都有
f x f x0 f x0 x x0 , xa,b x x0;
曲线的拐点
上例中点x b 就是一个拐点. 3a
定理２ 设 y f x 在 a,b内有连续的二阶导数, 若点
c a,b是 y f x 的拐点，则 f c 0.
证 用反证法 . 设f (c) 0,不妨设f (c) 0.由f (x)的连续性，
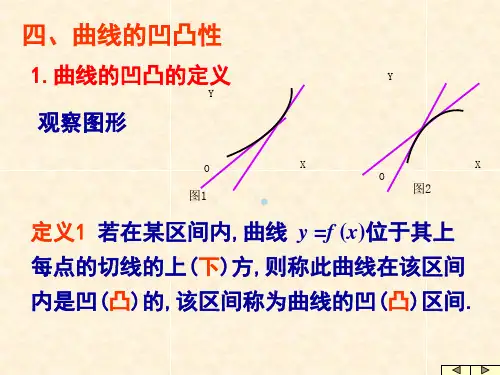
是曲线y f (x)的过点（ x0, f (x0 ))的切线方程， f (x)在(a,b)上
向上凸, 曲线弧总是在它的切线的下方， f (x)在(a,b)上 向下凸, 曲线弧总是在它的切线的上方.
定理1 (曲线凹凸性的判定法)
设f(x)在(a, b)内具有二阶导数, 对于每一点 x a,b
必存在c的一个邻域 U（ c), 使
f (x) 0, x U (c). 由定理1，f (x)在整个U (c)内都是向下凸的 , 不论x是在c的左 侧附近还是在 c的右侧附近 , 这与c是拐点矛盾. 证毕.
二阶导数为零仅是拐点的必要条件，但不是充分条件.
补例 判断曲线
的凹凸性.
y
解 y 4x3,
f x0 0或不存在.
如果在 x0的左右两侧
f x异号, 则 x0, f x0
拐点
是拐点.
补例 求曲线
的拐点.
2
5
解
y

1 3
x

第四、六节 曲线凹凸性及函数图形描绘

第四、六节 曲线凹凸性及函数图形描绘
x→x0 x→x0 x→x0
x 则 = x0是 数 = f ( x)的 条 直 近 . 函 y 一 垂 渐 线
y C o x y o
x0
x
曲 例1 求 线 y =
1 的 平 近 . 水 渐 线 x −1
y
2 1 -2 -1 -1 -2
y = ( x −1)
−1
1 解 Qlim =0 x→ x −1 ∞
1 一条水平渐近线 ∴ y = 0 是y = x −1
1 曲 的 垂 近 . 铅 渐 线 例2 求 线 y = x −1
O 1
2
x
1 1 解 Qlim = −∞, lim = +∞, − + x→ x −1 1 x→ x −1 1
∴x =1 y = f (x)的 条 垂 近 . 为 一 铅 渐 线
利用导数工具描绘函数的图形，称为分析法作图. 利用导数工具描绘函数的图形，称为分析法作图. 分析法作图
[ (2) f ′′( x) < 0, 则 ( x)在a,b]上的图形是凸的 f .
例1 判断函数 y = ln x的凹凸性 . 解 y 的定义域为 (0,+∞ )
1 Q y′ = x
y ′′ = − 1 x2
∴ 在(0， ∞ )内，有 y′′ < 0 +
例2 判断 y = x 3 的凹凸性 . 解
2 y ′′ = 36 x − 24 x = 36 x x − 令 y′′ = 0 3 列表
x2 =
2 3
x y" y
(−∞,0)
0 0
1(拐点)
2 , 0 3
+
－
0
11 (拐 ) 点 27

函数的性质曲线的凹凸性与分析作图法

函数的性质曲线的凹凸性与分析作图法

2 (2,3)
3 (3,)
y
-
不存在
+
0
-
y f (x)
拐点
(2, 20 )
9
拐点
(3, 4)
结论：(,2],[3,)是曲线的凸区间,[2,3]是
曲线的凹区间； 拐点为 (2, 20), (3,4).
9
例 求曲线 y x 4 的凹凸区间和拐点
（学生练习）
例 求曲线 y earctanx的凹凸区间和拐点
y 1 x
P
x
O
点P 沿着曲线无限地远离原点时,
点P与一条定直线C 的距离趋于零, 则称直线C为曲线L的渐近线.当C 垂直于x 轴时,
称C为曲线 L的垂直渐近线；当C 垂直于y 轴时,
称C为曲线 L的水平渐近线.
y ex
ytanx
说明:
(1)直线 y y 0 是曲线 y f (x) 的水平渐近线
x0
2.曲线凹凸的判别
y=f(x)
X
观察图形中切线的斜率变化情况.
f (x) 0Y
在图1中,
Y
f (x) 0
当 x1 x2 时,
O 1 2
X
tan1tan2, 图1
2 1
X
O
图2
即 f ( x ) 是单调增加的;
在图2中,当 x1 x2 时,tan1tan2,
即 f ( x ) 是单调减少的.
三、函数的分析作图法
例 作 y 1 x 3 x 的图象 3
解(1)定义域 x(,), 并 且 图 象 关 于 原 点 对 称 .
(2) y x2 1, 得驻点 x11,x21.
y 2x, 令 y 0 得 x 0.

《函数凹凸性》课件

《函数凹凸性》课件
几何意义
在函数图像上，凸函数表现为图像位于其连接直线的上方。
凹凸函数的几何意义
凹函数的几何意义
在凹函数的图像上，任意两点之间的线段都位于这两点之间函数的曲线下方。这 表明，对于凹函数，中点的函数值总是大于或等于两端点连线上中点的函数值。
凸函数的几何意义
在凸函数的图像上，任意两点之间的线段都位于这两点之间函数的曲线上方。这 表明，对于凸函数，中点的函数值总是小于或等于两端点连线上中点的函数值。
几何意义
在函数图像上，凹函数表现为图像位于其连接直线的下方。
凸函数的定义
凸函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1, x_2$（ $x_1 < x_2$）都有$f(x_1) + f(x_2) < 2f[(x_1 + x_2)/2]$， 则称$f(x)$在区间$I$上是凸函数。Βιβλιοθήκη 4凹凸性在优化问题中的应用
利用凹凸性求解优化问题
01
确定函数的凹凸性
首先需要判断函数的凹凸性，可以通过求二阶导数或观察函数图像来进
行判断。
02 03
利用凹凸性寻找极值点
在确定了函数的凹凸性之后，可以利用凹凸性寻找函数的极值点。在凹 函数中，极值点出现在二阶导数为0的点；在凸函数中，极值点出现在 边界点或一阶导数为0的点。
有$f(x_1) + f(x_2) < 2fleft(frac{x_1 + x_2}{2}right)$，则称$f(x)$在区间$I$上是凸函数。
二次导数法
总结词
通过判断一阶导数的正负来判断函数 凹凸性的常用方法
详细描述
如果函数$f(x)$的二阶导数$f''(x) > 0$，则函数$f(x)$为凹函数；如果二 阶导数$f''(x) < 0$，则函数$f(x)$为 凸函数。这种方法适用于一阶导数容 易计算或形式较为简单的函数。

高数课件14凹凸性

高数课件14凹凸性

凹凸性与光滑性 的应用：在优化 问题、微分方程 等领域有广泛应 用
凹凸性与函数的单调性
凹凸性：函数在某点处的二阶导数符号决定了该点的凹凸性
单调性：函数在某点处的一阶导数符号决定了该点的单调性
凹凸性与单调性的关系：凹凸性与单调性是函数在某点处的二阶导数和一阶导数的符号决定的
凹凸性与单调性的应用：在解决实际问题时，可以利用凹凸性与单调性来判断函数的极值和拐 点
利用极限判断： 如果极限存在且 大于0，则为凹 函数；如果极限 存在且小于0， 则为凸函数。
03
凹凸性的性质
凹凸函数的性质
01 02
03 04
05 06
凸函数：对于任意x1, x2, y1, y2，若x1 < x2，则f(x1) < f(x2) 凹函数：对于任意x1, x2, y1, y2，若x1 < x2，则f(x1) > f(x2) 凸函数的二阶导数大于等于0
正二阶导数：函数在该点处 为凸函数
负二阶导数：函数在该点处 为凹函数
注意事项：凹凸性判定法只 适用于二阶可导的函数
06
凹凸性的扩展知识
凹凸性的连续性和可微性
凹凸性的连续性：凹凸性是函数 在某点附近的局部性质，与函数 的连续性无关
凹凸性的可导性：凹凸性是函数 在某点附近的局部性质，与函数 的可导性无关
凹凸性与函数极值的关系
凹凸性是函数在某点附近的性质，与函数在该点的极值有关 凸函数在极小值点处具有凹性，凹函数在极大值点处具有凸性 凸函数的极小值点处，其导数大于等于0 凹函数的极大值点处，其导数小于等于0 凸函数的极小值点处，其二阶导数大于等于0 凹函数的极大值点处，其二阶导数小于等于0
感谢观看
汇报人：

函数的凹凸性与作图.ppt

函数的凹凸性与作图.ppt

机动 目录 上页 下页 返回 结束
例5：证明不等式
例5.4 例5.5
1 (xn yn ) ( x y )n (x 0, y 0, x y, n 1)
2
2
证明：设 f (t) tn (t 0,n 1) 则
f (t) ntn1, f (t) n(n 1)tn2,
当 t 0,n 1 时，有 f (t) 0
x x x k lim f (x)
x x
(或x )
lim [ f (x) k b ] 0
x x
x
b lim [ f (x) kx]
x (或x )
机动 目录 上页 下页 返回 结束
例2. 求曲线
的渐近线 .
解: y
x3
, lim y ,
(x 3)(x 1) x3
(或x 1)
即上述 f（t）为下凸函数，于是对任意 x 0, y 0 有：
1 (xn yn) ( x y)n
2
2
二、 曲线的渐近线
定义3 . 若曲线 C上的点M 沿着曲线无限地远离原点
时, 点 M 与某一直线 L 的距离趋于 0, 则称直线 L 为
曲线C 的渐近线 .
y
y f (x)
或为“纵坐标差” C M y k x b
例如, 双曲线
L PN
o
x
有渐近线
x y0
y
ab
但抛物线
无渐近线 .
ox
机动 目录 上页 下页 返回 结束
1. 水平与铅直渐近线
若
则曲线
有水平渐近线 y b.
(或x )
若
则曲线
有垂直渐近线 x x0 .
(或x x0 )

函数曲线的凹凸性与作图

函数曲线的凹凸性与作图

（2）y
8
x3
5
x 3，y
8
5
x3
5
2
x 3，y
40 x
10
.
33
93 x
（3）令y 0，得x 1，又当x 0时，y不存在，故有表3 - 5所示的区间. 4
表3-5
函数曲线的凹凸性与作图
综上所述，判定曲线y f x的凹凸及拐点的步骤归纳如：
（1）求函数的定义域；
（2）求函数的一阶导数f x和二阶导数f x； （3）求出f x 0和f x不存在的点； （4）对步骤（3）求出的每一个点，检查其左、右邻近的f x的符号，如果异号，则该点为曲
（1）确定函数的定义域和值域； （2）确定曲线关于坐标轴的对称性； （3）求出曲线和坐标轴的交点； （4）判断函数的单调区间并求出极值； （5）判断函数的凹凸区间和拐点； （6）求出曲线的渐近线； （7）列表讨论并描绘函数的图像.
函数曲线的凹凸性与作图
例5
解
（1）定义无对称性.
0
曲线y f x的垂直渐近线(垂直于x轴).
（2）水平渐近线.对于曲线 y f x，若 lim f x A或 lim f x A,则直线y A是曲
x
x
线y f x的水平渐近线（平行于x轴）.
（3）斜渐近线 . 对于曲线y f x，若 lim f x a，lim[ f x ax] b，则直线 y ax b
定义2
若曲线C上的动点P沿曲线无限地远离原点时，动点P到某一固定直线L的距 离趋于零，则称直线L为曲线C的渐近线.
函数曲线的凹凸性与作图
曲线的渐近线有垂直渐近线、水平渐近线和斜渐近线三种.
（1）垂直渐近线.对于曲线y
f
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
机动 目录 上页 下页 返回 结束
6）绘图
x ( , 1) 1 (1,1)
y
1
无 定 义
(1, 3) 3
(3 , )
2
(极大)
0
(极小)
铅直渐近线 斜渐近线 特殊点
x 1 1 5 y x 4 4
( x 3) 2 y 4( x 1)
x
y
0 9 4
2 1 4
3) 判别曲线形态
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )



(极大)
机动
(拐点)
目录 上页 下页 返回 结束
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )



(极大)
(拐点)
4) 求渐近线
y
A
1 2
lim y 0
( k x b)
f ( x) b k lim [ ] x x x f ( x) k lim x x
(或 x )
f ( x) b lim x[ k ]0 x x x f ( x) b lim [ k ]0 x x x
b lim [ f ( x) k x]
y
C M
y f ( x)
y kxb
L
PN
有渐近线
但抛物线
x y 0 a b
无渐近线 .
o
y
x
x
o
机动
目录
上页
下页
返回
结束
1. 水平与铅直渐近线 若 则曲线
(或 x )
有水平渐近线 y b . 有垂直渐近线 x x0 .
若
(或 x x0 )
则曲线
例1. 求曲线
的渐近线 .
2 1
1 解: lim ( 2) 2 x x 1
y 2 为水平渐近线; 1 lim ( 2) , x 1为垂直渐近线. x1 x 1
机动 目录 上页 下页 返回 结束
2. 斜渐近线 若
(或 x )
( k x b)
斜渐近线 y k x b .
2 4 y 8 y 4 x y 0 1 4 y y 2( x 1)
令 y 0 得 x 1, 3 ;
机动 目录 上页 下页 返回 结束
3) 判别曲线形态
x ( , 1) 1 (1,1) y 0 y y 2
1
0 12 3
机动
目录
上页
下页
返回
结束
例5. 描绘函数
解: 1) 定义域为 2) 求关键点 2 x 1 xe 2 , y 2
的图形. 图形对称于 y 轴.
1 y e 2
2 x 2
(1 x 2 )
令 y 0 得 x 0 ; 令 y 0 得 x 1
f (1) f (0) f ( ) (0 1)
机动 目录 上页 下页 返回 结束
3)
1
1 2 3
x ( , 0) y y y x 1 3 y 2 2 3
0 0
(0 ,1)
1
0
4 3
(1, 2)



2 ( 2 , ) 0
2 3
2
(极大)
(拐点）
(极小)
4)
机动
目录
上页
下页
返回
结束
例4. 描绘方程
的图形.
( x 3) 2 , 定义域为 解: 1) y 4( x 1) 2) 求关键点 2( x 3) 4 y 4 y 4 x y 0 x 3 2y y 2( x 1)
机动
目录上页ຫໍສະໝຸດ 下页返回结束
令
得：
机动
目录
上页
下页
返回
结束
充分性： 设
单调增加， 对函数
分别在区间
上用拉格朗日中值定理得：存在
机动
目录
上页
下页
返回
结束
定理2.(凹凸判定法) 设函数 (1) 在 I 内 (2) 在 I 内 证: 则
在区间I 上有二阶导数 在 I 内图形是下凸的 ;
则 在 I 内图形是上凸的 . 利用一阶泰勒公式可得
x
y
1 2
e

x2 2
y 0 为水平渐近线
5) 作图
B
o
x
机动
目录
上页
下页
返回
结束
思考与练习
1. 曲线 y
1 e
x2
2
1 e x
(D )
(B) 仅有水平渐近线；
(A) 没有渐近线；
(C) 仅有铅直渐近线；
(D) 既有水平渐近线又有铅直渐近线. 提示: lim
1 e
f (1 ) x1 x2 x1 x2 x1 x2 2 x1 x2 f ( x1 ) f ( ) f ( ) ) ( x1 ) 2 ! ( x1 2 2 2 2 x1 x2 x1 x2 f ( 2 ) x1 x2 x1 x2 2 )( x2 f ( x2 ) f ( ) f ( ) ) 2 ! ( x2 2 2 2 2 两式相加
(0 , )

上凸
的拐点 .
机动
目录
上页
下页
返回
结束
说明:
1) 若在某点二阶导数为 0 , 在其两侧二阶导数不变号, 则曲线的凸性不变 . 2) 根据拐点的定义, 可得拐点的判别法如下: 若曲线 的一个拐点. 或不存在, 但 f ( x) 在 x0 两侧异号, 则点( x0 , f ( x0 )) 是曲线
x1 x2 f ( x1) f ( x2 ) 2 f ( ) 2
f ( x1 ) f ( x2 ) 2
(
1 2!
x2 x1 2 [f 2
)
(1 ) f ( 2 )]
当 f ( x) 0时,

x1 x2 f( ), 2
说明 (1) 成立; (2) 证毕
x2 x
返回 结束
(2) 若恒有
则称 图形是上凸的; 或称f (x)为I上的上凸函数。
弦在弧的下方；切线在曲线的上方。
下凸也称为凸，上凸也称为凹。 y
o
x1
x1 x2 2
x2 x
机动
目录
上页
下页
返回
结束
等价定义： 定义1´：设函数 在区间 I 上连续 ,
(1) 若恒有
则称
图形是下凸的; （弦在弧的上方，或切线在曲线下方） (2) 若恒有 则称
(极大)
(1, 3) 3 0 无 定
1
(3 , )
义

0
(极小)
4) 求渐近线
lim y , x 1 为铅直渐近线
x1
( x 3)( x 1) 2 ( x 3) , y y , y 2 4( x 1) 4( x 1) ( x 1)3
机动 目录 上页 下页 返回 结束
例5：证明不等式
例5.4 例5.5
1 n x y n n (x y ) ( ) ( x 0, y 0, x y, n 1) 2 2
证明：设 f (t ) t n (t 0, n 1)
则
f (t ) nt n1, f (t ) n(n 1)t n2 ,
3
1
2 x 2 3x b lim [ f ( x) x] lim 2 x x x 2 x 3
y x 2 为曲线的斜渐近线 .
机动 目录 上页 下页 返回 结束
三、函数的作图
步骤 : 1. 确定函数 期性 ; 的定义域 , 并考察其对称性及周 并求出 及 为 0 和不存在
第五节
第三章
曲线的凸性与函数作图
一、曲线的凸性
二、渐近线 三、函数的作图
机动
目录
上页
下页
返回
结束
一、曲线的凸性
定义1 . 设函数 在区间 I 上连续 ,
(1) 若恒有
则称
图形是下凸的; 或称f (x)为I上的下凸函数。
B
弦在弧的上方；切线在曲线的下方。
A
y
o
机动
x1
目录
x1 x2 2
上页 下页
机动 目录 上页 下页 返回 结束
2
y 1 1 又因 lim , 即 k x x 4 4 2 ( x 3 ) 1 1 x] b lim ( y x) lim [ x 4( x 1) 4 x 4 5x 9 5 lim 2 ( x 3 ) x 4( x 1) 4 y 4( x 1) 1 5 y x 为斜渐近线 ( x 3)( x 1) 4 4 y 4( x 1) 2 0 2 5) 求特殊点 x 2 1 y y 9 3 ( x 1 ) 4 4
( A) ( B) (C ) ( D)
f (1) f (0) f (1) f (0) f (1) f (1) f (0) f (0) f (1) f (0) f (1) f (0) f (1) f (0) f (1) f (0)
提示: 利用 f ( x) 单调增加 , 及
x (或 x )
机动 目录
上页
下页
返回
结束
例2. 求曲线
的渐近线 .
x3 解: y , lim y , ( x 3)(x 1) x3