高三高考数学复习之凹凸函数之切线放缩

由题意，f′(x)＝1x－(x＋1)ex＋a≤0 在[1，＋∞)上恒成立， 从而 a≤(x＋1)ex－1x， 设 g(x)＝(x＋1)ex－1x(x≥1)， 则 g′(x)＝(x＋2)ex＋x12>0， 所以g(x)在[1，＋∞)上单调递增，故g(x)min＝g(1)＝2e－1，
因为a≤g(x)恒成立，所以a≤2e－1，
方法一 (切线放缩，利用ex≥x＋1)
对任意的x>0，f(x)≤xe2x 恒成立，
xe2x－ln x＋1
等价于 a≤
x
在(0，＋∞)上恒成立.
因为xe2x－(ln x＋1)＝e2x＋ln x－(ln x＋1)≥(2x＋ln x＋1)－(ln x＋1)＝2x，
xe2x－ln
所以
x
x＋1≥2xx＝2.
所以h′(x)>0⇔－2<x<－1，h′(x)<0⇔x>－1， 从而h(x)在(－2，－1)上单调递增，在(－1，＋∞)上单调递减， 故h(x)max＝h(－1)＝0，所以h(x)≤0， 故ln(x＋2)≤x＋1，当且仅当x＝－1时等号成立， 综上所述，有ln(x＋2)≤x＋1≤ex，且两个等号不能同时成立， 所以ln(x＋2)<ex， 故ex－ln(x＋2)>0， 因为当m≤2时，f(x)＝ex－ln(x＋m)≥ex－ln(x＋2)，所以f(x)>0.
即e2x0 ＝x10，2＝－lnx0x0， 所以 m(x)≥m(x0)＝e2x0－ln xx00＋1＝x10－lnx0x0－x10＝2，则有 a≤2，
所以实数a的取值范围为(－∞，2].
考点二 利用切线放缩证明不等式
典例2 已知函数f(x)＝ex－ln(x＋m). (1)设x＝0是f(x)的极值点，求m的值，并讨论f(x)的单调性；

第12讲切线放缩本讲义由作业帮周永亮老师（白哥）独家编撰，侵权必究知识导航1．两个常见的切线放缩公式（1） ;（2）2．切线放缩在求导过程中的应用在求导的过程中，我们很多时候需要求二次导，乃至三次或多次，其实，对于几乎所有的问题，如果我们能够很好的利用放缩的技巧的话，我们最多只需要求二次导就可以了.3．切线放缩在数列不等式中的应用数列不等式有很多种，其中有一种最常见的叫做“拆和之函数放缩”，而这个函数，一般都是由我们这两个最常见的切线放缩公式演变而来的．知识札记例2（★★★☆☆）（2018·河北石家庄市一模）已知函数（）在处的切线方程为．（1）求，．（2）若，证明：．例1（★★★☆☆）（2018·河北保定市模拟【文】）已知函数，函数，证明：当且时，．考点1 切线放缩的基础应用注：本讲对于切线放缩公式的应用，都写了易证，但在正常考试中，需要同学们证明.经典例题例5（★★★★☆）（2017·黑龙江大庆市期中【文】）已知，求证：当时，恒成立．例4（★★★★☆）已知函数，在点处的切线方程为．（1）求，；（2）证明：．例3（★★★★☆）证明：．考点2 切线放缩拓展应用例8（★★★★☆）证明：当，时，．考点3 切线放缩在数列不等式中的应用例7（★★★★★）证明：．例6（★★★★★）（2018·江苏泰州市期末【文】）已知函数，（，），当，时，求证：．例11（★★★★☆）（2013·安徽合肥市月考【理】）设函数（），数列满足：，（）．（1）求数列的通项公式；（2）求证：．例10（★★★★☆）（2018·辽宁月考【文】）求证：（）．例9（★★★★☆）（2016·湖南模拟【理】）证明不等式：（）．课后练习练1（★★★☆☆）（2017·贵州一模【文】）已知函数，证明：对任意，成立．练2（★★★★★）（2017·重庆渝中区模拟【理】）已知函数（为实数，为自然对数的底数），曲线在处的切线与直线平行．（1）求实数的值；（2）证明：当时，．练3（★★★★☆）（2016·全国卷）求证：当且时，．。

导数中证明不等式技巧——构造、切线放缩、二元变量、凹凸反转,唯手熟尔!导数中的不等式证明导数中的不等式证明是高考中的一个经典考点。

由于不等式证明的灵活性和多样性，该考点备受命题者的青睐。

本文将从五个方面系统地介绍一些常规的不等式证明手段。

命题角度1：构造函数典例1】（赣州市2018届高三摸底考试）已知函数$f(x)=1-\ln x+\frac{e}{x}$，$g(x)=x-\frac{e}{x}$，若曲线$y=f(x)$与曲线$y=g(x)$的一个公共点是$A(1,1)$，且在点$A$处的切线互相垂直。

求$a,b$的值，并证明当$x\geq1$时，$f(x)+g(x)\geq\frac{2}{x}$。

解析】（1）$a=b=-1$；2）$g(x)=-\frac{e}{2\ln x}+\frac{x}{2}-\frac{e}{2x}$，$f(x)+g(x)\geq\frac{2}{x}$ $\Leftrightarrow 1-\frac{1}{x}+\frac{e}{x}-\frac{e}{2\ln x}+\frac{x}{2}-\frac{e}{2x}\geq\frac{2}{x}$ $\Leftrightarrow\frac{1}{x}+\frac{ e}{2\ln x}-\frac{x}{2}+\frac{e}{2x}\leq1$。

令$h(x)=f(x)+g(x)-\frac{2}{x}$，则$h(x)=1-\frac{1}{x}+\frac{e}{x}-\ln x-\frac{e}{2\ln x}+\frac{x}{2}-\frac{e}{2x}$，$h'(x)=-\frac{1}{x^2}+\frac{e}{x^2}-\frac{1}{x}-\frac{e}{2x^2}+\frac{1}{2}-\frac{e}{2x^2}$，$h''(x)=\frac{2}{x^3}-\frac{3e}{x^3}+\frac{2e}{x^3}$。

点P处的切线。
单切线放缩
例1.求证:当x>0时，1+2x<e2x
例1：
单切线放缩
例2：
注：（1）该方法适用于凹函数与凸函数且它们的凹凸性相反
的问题（拆成两个函数）； ----数形结合
（2）两函数有斜率相同的切线，这是切线放缩的基础。引入
一个中间量，分别证明两个不等式成立，然后利用不等式的传
递性即可；
明.
小结
1.切线放缩法实质是以直（切线）代曲（原函数）；
2.切线放缩法中常用的两个定理必须先证明后使用；
3.证明流程为：求切线—构造差函数—证明差函数恒正
（负）--原不等式成立．
4.对于较为简单的导数试题，往往只涉及到一次切线放缩，
但是有些压轴试题涉及到两次不同的切线放缩．
----以直代曲
（3）难点在合理拆分函数，寻找它们斜率相等的切线隔板.
单切线放缩
例3：
略，
注：含参函数有时需要根据函数特征将原函数进行适当放缩.
单切线放缩
例4：
注：复杂形式的函数需要将函数适当转化后再进行放缩.
双切线放缩
例5：
a>1
注：含有两个零点的f(x)的解析式(可能含有参数, )，
告知方程f(x)=b有两个实根，要证明两个实根之差小于
(或大于)某个表达式．求解策略是画出f(x)的图象，并
求出f(x)在两个零点处(有时候不一定是零点处)的切线
方程(有时候不是找切线，而是找过曲线上某两点的直
线)，然后严格证明曲线f(x)在切线(或所找直线)的上
方或下方，进而对, 作出放大或者缩小，从而实现证
导数的应用
--切线放缩法证明不等式
复习引入：曲线在某一点处的切线的定义

第30讲双参数最值问题知识与方法含参问题一直是高考中的重点与难点. 高考真题及模拟题中常出现“恒成立”为背景的双参数的范围或最值问题. 处理此类问题, 常用有以下方法:1消元法2零点比大小法零点比大小是指将函数y=ax+b与函数y=f(x)的零点比较大小, 进而解决问题. 图象上看, 是观察直线y=ax+b与曲线y=f(x)的横截距的大小关系. 此方法要求y=f(x)函数具有凹凸性, 可以解决形如“已知ax+b⩾f(x) (或⩽f(x))恒成立, 求b的最值”的问题,一般有如下两种形式:k(1) 若ax+b⩾f(x)恒成立, f(x)为上凸函数, 如下左图, 则x1⩽x2;(2) 若y=ax+b⩽f(x)恒成立, f(x)为下凸函数, 如下右图, 则x1⩾x2.的最值.由(1)或(2)得出x1,x2的大小,进而可以求得bk3. 赋值法对比不等式与目标式的结构, 发现当自变量取某个值时恰好构造出目标式.赋值法是零点比大小法方法的优化和改进,能快速解决线性表达式型、比值型的客观题 . 点睛意领会“等比例赋值法”进行恰到好处的赋值.典型例题【例1】若(x2+x)ln⁡1x −ax⩽23x3+(1−a)x2−2ax+b恒成立, 求b−2a的最小值 .【答案】−53【解析】解法 1: 消元法设F(x)=23x3+(1−a)x2−2ax+b−(x2+x)ln⁡1x+ax,则F′(x)=(2x+1)(ln⁡x+x+1−a),令ℎ(x)=ln⁡x+x+1−a得ℎ(x)单调递增, 故存在唯一x0使得ℎ(x0)=0, 即a= x0+ln⁡x0+1当x∈(0,x0)时, F(x)单调递减当x∈(x0,+∞)时, F(x)单调递增,故F(x)min=F(x0)=−13x03−x02−x0+b.所以F(x)min=F(x0)⩾0, 即b⩾13x03+x02+x0,b−2a⩾13x03+x02−x0−2ln⁡x0−2,t(x)=13x3+x2−x−2ln⁡x−2,t′(x)=(x−1)(x2+3x+2)x,当x∈(0,1),t(x)单调递减; 当x∈(1,+∞),t(x)单调递增,故 t(x)min =t(1)=−53. 所以 b −2a 的最小值为 −53.解法 2: :赋值法f(x)⩽g(x)⇔b −(x 2+x )a ⩾−(x 2+x )ln⁡x −23x 3−x 2令 x 2+x =2 (等比例赋值法), 解得 x =1 (舍 x =−2 ), 则 b −2a ⩾−53.当 b −2a =−53 时, 由 f(x)−g(x)⩽0=f(1)−g(1) 知 x =1 是 f(x)−g(x) 的极值点,所以 f ′(1)−g ′(1)=0, 解得 a =2,b =73.下面证明: 当 a =2,b =73时, f(x)⩽g(x).证明:令 ℎ(x)=g(x)−f(x)=23x 3−x 2−2x +73+(x 2+x )ln⁡x .则 ℎ′(x)=(2x +1)(x −1+ln⁡x),当 x >1 时, ℎ′(x)>0,ℎ(x) 递增; 当 0<x <1 时, ℎ′(x)<0,ℎ(x) 递减.所以 ℎ(x)⩾ℎ(1)=0, 即 f(x)⩽g(x) 恒成立.综上可知, b −2a 的最小值为 −53.【点睛】求线性表达式型 ma +nb(m,n 为常数) 的最值时, 赋值的要点在于把原不等式变 成关于 a,b 的二元一次不等式, 然后根据 a,b 的系数比与 m:n 相等求出 x 0 (简称等比例赋值法 ).【例2】若函数 f(x)=aln⁡x +12x 2+2bx 在区间 [1,3] 上单调递增, 则 a +4b 的最小值为 .【答案】−4【点睛】这里用了等比【例】赋值法, 要点睛意等号成立的条件. 由已知得ax+2b+x⩾0对x∈[1,3]恒成立, 与目标式a+4b比较, 令1x:2=1:4, 得x=2, 因此令x= 2. 当a+4b=−4时, 由g(x)⩾0=g(2)知x=2是g(x)的极值点, 所以g′(2)=0⇒a=4,b=−2.比值型【例3】已知函数f(x)=ln⁡x+(e−a)x−2b, 若不等式f(x)⩽0对x∈(0,+∞)恒成立, 则ba的最小值为 .【答案】- 12e.【解析】解法 1 : 消元法显然a>e,f′(x)=1x +(e−a), 易知x=1a−e为f(x)的极大值点,所以只需f(1a−e )⩽0, 即2b⩾−ln⁡(a−e)−1, 所以2ba⩾−ln⁡(a−e)−1a.今ेℎ(a)=−12⋅[ln⁡(a−e)+1]a,则ℎ′(a)=−12⋅ea−e−ln⁡(a−e)a2, 点睛意到ℎ′(2e)=0,易知a=2e为ℎ(a)的极小值点, ℎ(2e)=−12e .所以ba⩾−12e, 故ba的最小值为−12e.解法 2:零点比大小f(x)⩽0⇔ln⁡x+(e−a)x−2b⩽0⇔ln⁡x+ex⩽ax+2b, 即ln⁡x+ex⩽a(x+2ba)函数y=ln⁡x+ex与y=a(x+2ba )的零点分别为1e,−2ba由图可知: −2ba ⩾1e⇒ba⩽−12e, 故ba的最小值为−12e.解法 3 : 赋值法f(x)⩽0⇔ln⁡x +ex ⩽ax +2b , 令 x =1e , 则 a ⋅1e +2b ⩾0⇒ba ⩾−12e .故 ba的最小值为 −12e.【点睛 1】求比值型的最值时, 赋值的要点在于把原不等式改写成一边只含有目标式分子、 分母的线性结构, 再令另一边为 0 , 找到 x 0.【点睛 2】观察不等式 ln⁡x +ex ⩽ax +2b 与目标式 ba 的结构, 进行恰到好处的赋值. 只需 让 ln⁡x +ex =0, 便得 a ⋅1e+2b ⩾0, 进而可求得 ba的最值. 解方程 ln⁡x +ex =0, 可得 x =1e , 从而有上面的解法.【点睛 3】本题我们用了消元法、零点比大小和赋值法, 显然赋值法最为简捷.【例4】已知不等式 (e −a)e x +x +b +1⩽0 恒成立, 其中 e 为自然常数, 则 b+1a的最大值 为 .【答案】 1e【解析】赋值法(e −a)e x +x +b +1⩽0⇔ae x −(b +1)⩾e x+1+x , 令 e x+1+x =0, 得 x =−1, 则 a ⋅1e −(b +1)⩾0⇒b+1a⩽1e , 故b+1a的最大值为 1e .乘积型【例5】若e x−x+12x2⩾12x2+ax+b恒成立, 求(a+1)b的最大值.【答案】e2【解析】解法 1 : 消元法e x−x+12x2⩾12x2+ax+b⇔e x−(a+1)x−b⩾0,令g(x)=e x−(a+1)x−b, 则g′(x)=e x−(a+1),(1)若a+1<0, 则g′(x)>0, 则g(x)=e x−(a+1)x−b在R上单增,当x→−∞时, f(x)→−∞,与g(x)⩾0矛盾, 舍去.(2)若a+1>0, 由g′(x)=0得x=ln⁡(a+1),所以g(x)在(−∞,ln⁡(a+1))单减, 在(ln⁡(a+1),+∞)单增, 则g(x)min=g(ln⁡(a+ 1))=(a+1)−(a+1)ln⁡(a+1)−b⩾0,即b⩽(a+1)−(a+1)ln⁡(a+1)，则b(a+1)⩽(a+1)2−(a+1)2ln⁡(a+1)令ℎ(t)=t2−t2ln⁡t,t>0, 则ℎ′(t)=t−2tln⁡t=t(1−2ln⁡t)所以ℎ(t)在(0,√e)单增, (√e,+∞)单减, 所以ℎ(t)max=ℎ(√e)=e2,(3) 当a+1=0时, (a+1)b=0,综上: (a+1)b最大值为e2.解法 2: 消元法e x −x +12x 2⩾12x 2+ax +b ⇔e x −(a +1)x −b ⩾0,即 b ⩽e x −(a +1)x(1) 若 a +1<0, 则 (a +1)b ⩾(a +1)e x −(a +1)2x ,令ℎ(x)=(a +1)e x −(a +1)2x,ℎ′(x)=(a +1)e x −(a +1)2=(a +1)[e x −(a +1)]<0所以当 x →−∞ 时, f(x)→+∞, 则 (a +1)b ⩾(a +1)e x −(a +1)2x 不成立(2) 若 a +1>0, 则 (a +1)b ⩽(a +1)e x −(a +1)2x ；令 ℎ(x)=(a +1)e x −(a +1)2x ,由 ℎ′(x)=0 得 x =ln⁡(a +1), 则 ℎ(x) 在 (0,ln⁡(a +1)) 单减, (ln⁡(a +1),+∞) 单增,所以 ℎ(x)=(a +1)2−(a +1)2ln⁡(a +1),令 g(t)=t 2−t 2ln⁡t,t >0, 则 g ′(t)=t −2tln⁡t =t(1−2ln⁡t),所以 g(t) 在 (0,√e) 单增, (√e,+∞) 单减, 所以 g(t)max =g(√e)=e2(3) 当 a +1=0 时, (a +1)b =0,综上: (a +1)b 最大值为 e2.【点睛】根据所求目标, 在 a,b 都在变的情况下, 求 (a +1)b 的最大值, 把 b 移到一边, 同乘以 (a +1), 构造出 (a +1)b , 在等式的右边成功地消灭了变量 b .【例6】已知函数 f(x)=e x −xa −b , 当实数 a >0 时, 对于 x ∈R 都有 f(x)⩾0 恒成立, 则 a 2b 的最大值为（）A. −1e2B. 1e2C. −2e2D. 2e2【答案】A【解析】f′(x)=e x−1a , 易知x=ln⁡1a为极小值点, 则f(x)min=f(1a)=1a+ln⁡aa−b⩾ 0 , 所以1a +ln⁡aa⩾b, 则a2b⩽a+aln⁡a, 令g(a)=a+aln⁡a, 易得g(a)min=g(1e2)=−1e2. 故a2b的最大值为−1e2.强化训练1.已知不等式ln⁡(x+1)−1⩽a(x+ba )对一切正数x恒成立, 则ba的最小值为 .【答案】1-e【解析】解法1:零点比大小ln⁡(x+1)−1⩽a(x+ba)恒成立,直线y=a(x+ba)在函数y=ln⁡(x+1)−1图象的上方,直线y=a(x+ba )在x轴上的截距为−ba,函数y=ln⁡(x+1)−1在(e−1,0)处的切线为y=1e[x−(e−1)],则 −ba⩽e −1⇒b a ⩾1−e , 故 (ba)min=1−e解法 2 : 赋值法取 x =e −1,便有 ba ⩾1−e2.已知函数 f(x)=2ax 2+bx −3a +1,x ∈[−4,4], 若 f(x)⩾0 恒成立, 则 5a +b 的取值 范围是当 5a +b 取得最小值时, a = .【答案】 a =121【解析】赋值法2ax 2+bx −3a +1⩾0,x ∈[−4,4], 即 (2x 2−3)a +xb +1⩾0,x ∈[−4,4]. 令，解得或则由 f(3)⩾0, 得 5a +b ⩾−13; 由 f (−12)⩾0, 得5a +b ⩽2.所以 5a +b 的取值范围是 [−13,2].当 5a +b =−13时, f(x)⩾0=f(3),可知 x =3 是函数 f(x) 的极值点 (或对称轴), 所以 −b 4a =3, 易得 a =121.3.已知不等式 x −3ln⁡x +1⩾mln⁡x +n(m ≠−3) 对 x >0 恒成立, 则 n−3m+3 的最大值为 .【答案】 −ln⁡2 【解析】赋值法，令，可得4.若对于任意正实数 x , 都有 ln⁡x −aex −b +1⩽0 (e 为自然对数的底数) 成立, 则 a +b 的最小值是 .【答案】0【解析】令x=1e, 代入得: a+b⩾0,以下说明a+b=0时满足条件,当a=1,b=−1时, 令f(x)=ln⁡x−ex+1+1=ln⁡x−ex+2,则f′(x)=1x −e=1−exx, 令f′(x)=0, 解得: x=1e,可知当x∈(0,1e )时, f′(x)>0, 当x∈(1e,+∞)时, f′(x)<0,故对任意正实数x, 都有f(x)⩽f(1e)=0,故a=1,b=−1时, a+b=0, 满足题意, 故a+b的最小值是 0 ,故答案为: 0 .5.已知不等式e x⩾ax+b(a,b∈R, 且a≠0)对任意实数x恒成立, 则b−2a的最大值为A. 2−ln⁡2B. 1−ln⁡2C. −2ln⁡2D. −ln⁡2【答案】D【解析】解法 1:零点比大小由e x⩾ax+b得e x−2⩾ax+(b−2)=a(x+b−2a),考虑y=e x−2与y=a(x+b−2a)在x轴上的截距,只需−b−2a ⩾ln⁡2⇒b−2a⩽−ln⁡2.解法 2 : 赋值法令e x−2=0即x=ln⁡2, 结合a>0, 立得b−2a⩽−ln⁡2.6.已知函数f(x)=e x−12x2+x3, 若x∈R时, 恒有f′(x)⩾3x2+ax+b, 则ab+ b的最大值为（）A. √eB. √e2C. e2D. e【答案】C【解析】因为函数f(x)=e x−12x2+x3, 则f′(x)=e x−x+3x2, 由题可知, 对x∈R, 恒有e x−x+3x2⩾3x2+ax+b⇒e x−x−ax−b⩾0成立, 令g(x)=e x−x−ax, 则g′(x)=e x−1−a当a<−1时, 函数g(x)在R上单调递增, 且x→−∞时, g(x)→−∞, 不符合题意;当a=−1时, ab+b=0, 当a>−1时, 令g′(x)=e x−1−a>0⇒x>ln⁡(1+ a),所以函数 g(x) 在 (ln⁡(1+a),+∞) 上单调递增, 且在 (−∞,ln⁡(1+a)) 上单调递减;所以 g(x)min =g[ln⁡(1+a)]=e ln⁡(1+a)−ln⁡(1+a)−aln⁡(1+a)=(1+a)− (1+a)ln⁡(1+a),故 (1+a)−(1+a)ln⁡(1+a)−b ⩾0⇒b(1+a)⩽(1+a)2−(1+a)2ln⁡(1+a),令 t =1+a >0, 则 ℎ(t)=t 2−t 2ln⁡t , 且 ℎ′(t)=2t −(2tln⁡t +t)=t(1−2ln⁡t),当 t ∈(0,√e) 时, ℎ′(t)>0, 函数 ℎ(t) 单调递增; 当 t ∈(√e,+∞) 时, ℎ′(t)<0, 函数ℎ(t) 单调递减,所以 ℎ(t)max =ℎ(√e)=(√e)2−(√e)2ln⁡√e =e2, 故 b(1+a)⩽e2, 综上所述, ab +b 的最大值为 e2.7.设函数 f(x)=ln⁡(ax +b)−x(a,b ∈R), 若 f(x)⩽0 恒成立, 则 ab 的最大值为 . 【答案】 e2【解析】 ln⁡(ax +b)⩽x 恒成立, 即 e x ⩾ax +b >0 恒成立, a,x,b >0e x ⩾ax +b ⩾2√ax ⋅b , 所以 ab ⩽e 2x 4x(x >0), 于是 ab ⩽(e 2x4x)min=e2.8.已知 a ≠0, 函数 y =f(x)=ae x ,y =g(x)=ealn⁡x +b ( e 为自然对数的底数), 若存在一 条直线与曲线 y =f(x) 和 y =g(x) 均相切, 则 ba 最大值是 【答案】e切线放缩知识与方法1. 切线放缩对于含有指数、对数或三角函数等超越式的函数或不等式问题, 有时我们可以利用导数的几何意义进行以直代曲, 即考虑函数f(x)图象上某点x=x0处的切线y=kx+b, 结合函数的凹凸性进行切线放缩, 使问题便于解决.特别地, 当f(x)⩾kx+b为下凸函数时, 则f(x)⩾kx+b; 当f(x)为上凸函数时, 则f(x)⩽kx+b. 两个不等式中等号成立的条件刚好是x=x0.将f(x)放大或缩小为kx+b, 得到f(x)⩾kx+b或f(x)⩽kx+b, (其中k=f′(x0),y=kx+b为f(x)在x=x0处的切线y=f′(x0)(x−x0)+f(x0))叫做切线放缩.对某些求函数的最小值或证明不等式的问题, 巧用切线放缩, 会有意想不到的效果.2. 常用的切线不等式x;(5)sin⁡x⩽x(x⩾0).(1) e x⩾x+1;(2)ln⁡x⩽x−1;(3)e x⩾ex;(4)ln⁡x⩽1e【点睛】在e x⩾x+1中, 将x换成ln⁡x, 即得x⩾ln⁡x+1⇒ln⁡x⩽x−1;在e x⩾x+1中, 将x换成x−1, 即得e x−1⩾x⇒e x⩾ex;x;在e x⩾ex中, 将x换成ln⁡x, 即得x⩾elnx⇔ln⁡x⩽1e在ln⁡x⩽x−1中, 将x换成x+1, 即得ln⁡(x+1)⩽x.典型例题逆用求导法则型【例1】若x,y是实数, e是自然对数的底数, e x+y+2−3⩽ln⁡(y−2x+1)+3x, 则2x+y= .【答案】- 83【解析】结合不等式e x⩾x+1 (当且仅当x=0时等号成立),可得: e x+y+2⩾(x+y+2)+1=x+y+3 (1),结合不等式ln⁡x⩽x−1 (当且仅当x=1时等号成立),则ln⁡(y−2x+1)⩽(y−2x+1)−1, 所以−ln⁡(y−2x+1)⩾2x−y(1) (2) 两式相加, 即得: e x+y+2−ln⁡(y −2x +1)⩾(x +y +3)+(2x −y)=3x +3 又已知 e x+y+2−3⩽ln⁡(y −2x +1)+3x ,所以 e x+y+2−3=ln⁡(y −2x +1)+3x , 于是(1)与 (2) 中的等号同时成立,所以 {x +y +2=0,y −2x +1=1, 解得 {x =−23,y =−43,所以 2x +y =−83. 故答案为: −83.【点睛】本题利用了夹逼法. 根据切线不等式 e x ⩾x +1 与 ln⁡x ⩽x −1, 并结合已知条件, 通过夹逼由不等式得到了方程, 最后点睛意到两个不等式中等号成立的条件, 解方程组即 可得到答案.【例2】已知函数 f(x)=ax +ln⁡x +1, 若对任意的 x >0,f(x)⩽xe 2x 恒成立, 则求实数 a 的 取值范围是 .【答案】 (−∞,2]【解析】解法 1: :切线放缩, 利用 e x ⩾x +1 对任意的 x >0,f(x)⩽xe 2x 恒成立,等价于 a ⩽xe 2x −(ln⁡x+1)x在 (0,+∞) 上恒成立.因为 xe 2x −(ln⁡x +1)=e 2x+ln⁡x −(ln⁡x +1)⩾(2x +ln⁡x +1)−(ln⁡x +1)=2x ,所以 xe 2x −(ln⁡x+1)x⩾2x x=2. 当且仅当 2x +ln⁡x =0 时等号成立 (方程显然有解),即 (xe 2x −(ln⁡x+1)x)min=2, 所以 a ⩽2.故答案为: (−∞,2].解法 2: 隐零点因为 f(x)=ax +ln⁡x +1, 所以对任意的 x >0,f(x)⩽xe 2x 恒成立, 等价于 a ⩽e 2x −ln⁡x+1x在 (0,+∞) 上恒成立.令 m(x)=e 2x −ln⁡x+1x(x >0), 则只需 a ⩽m(x)min 即可, 则 m ′(x)=2x 2e 2x +ln⁡xx 2,再令 g(x)=2x 2e 2x +ln⁡x(x >0), 则 g ′(x)=4(x 2+x )e 2x +1x>0, 所以 g(x) 在(0,+∞)上单调递增, 因为 g (14)=√e 8−2ln⁡2<0,g(1)=2e 2>0,所以 g(x) 有唯一的零点 x 0, 且 14<x 0<1,所以当 0<x <x 0 时, m ′(x)<0, 当 x >x 0 时, m ′(x)>0, 所以 m(x) 在 (0,x 0) 上单调递减, 在 (x 0,+∞) 上单调递增,因为 2x 02e 2x 0+ln⁡x 0=0, 所以 ln⁡2+2ln⁡x 0+2x 0=ln⁡(−ln⁡x 0), 即 ln⁡(2x 0)+2x 0=ln⁡(−ln⁡x 0)+(−ln⁡x 0) ， 设 s(x)=ln⁡x +x(x >0), 则 s ′(x)=1x +1>0, 所以函数 s(x) 在 (0,+∞) 上单调递 增,因为 s (2x 0)=s (−ln⁡x 0), 所以 2x 0=−ln⁡x 0, 即 e 2x 0=1x 0,2=−ln⁡x 0x 0,所以 m(x)⩾m (x 0)=e 2x 0−ln⁡x 0+1x 0=1x 0−ln⁡x 0x 0−1x 0=2, 则有 a ⩽2,所以实数a的取值范围为(−∞,2]. 故答案为: (−∞,2].【例3】已知a1,a2,a3,a4成等比数列, 且a1+a2+a3+a4=ln⁡(a1+a2+a3), 若a1>1, 则（）A. a1<a3,a2<a4B. a1>a3,a2<a4C. a1<a3,a2>a4D. a1>a3,a2>a4【答案】B【解析】(利用ln⁡x⩽x−1)由a1+a2+a3+a4=ln⁡(a1+a2+a3), 可得a1+a2+a3+a4=ln⁡(a1+a2+a3)⩽a1+a2+a3−1, 所以a4⩽−1, 故公比q<0. 若q⩽−1, 则a1+a2+a3+a4=a1(1+q)(1+q2)⩽0, 而a1+a2+a3=a1(1+q+q2)⩾a1>1, 即ln⁡(a1+a2+a3)>0, 矛盾; 所以−1<q<0, 所以a1−a3=a1(1−q2)> 0,a2−a4=a1q(1−q2)<0, 所以a1>a3,a2<a4, 故选B.多变量轮换式的切线放缩,x∈[0,3], 已知数列{a n}满足0<a n⩽3,n∈N∗, 且满足a1+【例4】f(x)=3+x1+x2a2+⋯+a2010=670, 则f(a1)+f(a2)+⋯+f(a2010)=A. 有最大值 6030B. 有最大值 6027C. 有最小值 6027D. 有最小值 6030【答案】A【解析】由 f(x)=3+x 1+x2(0⩽x ⩽3), 得 f ′(x)=−x 2−6x+1(1+x 2)2, 所以 f ′(13)=−910,f(x) 在x =13 处的切线方程为 y =−910x +3310, 下证 f(x)=3+x1+x 2⩽310(11−3x). 而 f(x)=3+x 1+x 2⩽310(11−3x)⇔(x −3)(x −13)2⩽0.因为 x ∈[0,3], 所以 (x −3)(x −13)2⩽0 成立, 故 f(x)=3+x 1+x 2⩽310(11−3x). 所以当 0<a n ⩽3,n ∈N ∗ 时, 有 f (a n )⩽310(11−3a n ),f (a 1)+f (a 2)+⋯+f (a 2010)⩽310[11×2010−3(a 1+a 2+⋯+a 2010)]=6030. 故 f (a 1)+f (a 2)+⋯+f (a 2010) 最大值 6030 .【点睛】本题利用函数 f(x)=3+x1+x 2 在 x =13 处的切线进行放缩, 思路如下: 点睛意到 a 1+ a 2+⋯+a 2010=670, 当 a 1=a 2=⋯=a 2010 时, 有 a 1=a 2=⋯=a 2010=13,即 13是各元相 等时候的平衡点, 于是求出函数在平衡点的切线方程 y =−910x +3310, 可得 f(x)⩽310(11−3x).双参数最值的切线放缩【例5】已知不等式 ln⁡(x +1)−1⩽a (x +ba ) 对一切正数 x 恒成立, 则 ba 的最小值为【解析】 ln⁡(x +1)−1⩽a (x +ba ) 恒成立,直线 y =a (x +ba ) 在函数 y =ln⁡(x +1)−1 图象的上方,直线y=a(x+ba )在x轴上的截距为−ba,函数y=ln⁡(x+1)−1在(e−1,0)处的切线为y=1e[x−(e−1)],则−ba ⩽e−1⇒ba⩾1−e, 故(ba)min=1−e【点睛】本题利用两函数的零点比较大小, 其实就是切线放缩.强化训练1.已知函数f(x)=e x−1,g(x)=ln⁡(x+1), 直线l与y=f(x)的图象相切, 与y= g(x)的图象也相切, 则直线的l方程是 .【答案】y=x【解析】f(x)=e x−1与g(x)=ln⁡(x+1)互为反函数, 其图象如图,其公共点为O(0,0),由f(x)=e x−1, 得f′(x)=e x, 所以f′(0)=1,曲线f(x)=e x−1在O(0,0)处的切线方程为y=x,由g(x)=ln⁡(x+1), 得g′(x)=1, 所以g′(0)=1,x+1曲线g(x)=ln⁡(x+1)在O(0,0)处的切线方程为y=x,所以曲线f(x)=e x−1与曲线g(x)=ln⁡(x+1)的公切线为y=x.故答案为: y=x.2.已知实数a,b,c满足e a+c+e2b−c−1⩽a+2b+1 (e 为自然对数的底数), 则a2+b2的最小值是 .【答案】15【解析】设u(x)=e x−(x+1), 则u′(x)=e x−1, 可知u(x)⩾u(0)=0, 即e x⩾x+1;由不等式性质可知e a+c+e2b−c−1⩾a+c+1+2b−c=a+2b+1, 当且仅当a+c= 2b30第 21 页 共 21页 −c −1=0 时取等号;又因为 e a+c +e 2b−c−1⩽a +2b +1,即有: e a+c +e 2b−c−1=a +c +1,所以 a +c =2b −c −1=0; 即 a =−c,b =c+12;所以 a 2+b 2=c 2+(c+1)24=54c 2+c 2+14=54(c +15)2+15⩾15当且仅当 c =−15 时取等号, 故 a 2+b 2 的最小值是 15, 答案为 :15.3.函数 f(x)=e x−a +x,g(x)=ln⁡(x +2)−4e a−x , 若 ∃x 0 使得 f (x 0)−g (x 0)=3, 则 a = .【答案】-1- ln⁡2 【解析】令 f(x)−g(x)=x +e x−a −1n(x +2)+4e a−x ,令 y =x −ln⁡(x +2),y ′=1−1x+2=x+1x+2,故 y =x −ln⁡(x +2) 在 (−2,−1) 上是减函数 (−1,+∞) 上是增函数,故当 x =−1 时, y 有最小值 −1−0=−1,而 e x−a +4e a−x ⩾4. ( 当且仅当 e x−a =4e a−x , 即 x =ln⁡2+a 时, 等号成立)。

第30讲双参数最值问题知识与方法含参问题一直是高考中的重点与难点. 高考真题及模拟题中常出现“恒成立”为背景的双参数的范围或最值问题. 处理此类问题, 常用有以下方法:1消元法2零点比大小法零点比大小是指将函数y=ax+b 与函数y=f(x) 的零点比较大小, 进而解决问题. 图象上看, 是观察直线y=ax+b 与曲线y=f(x) 的横截距的大小关系. 此方法要求y=f(x) 函数具有凹凸性, 可以解决形如“已知ax+b⩾f(x) (或⩽f(x)) 恒成立, 求bk 的最值”的问题,一般有如下两种形式:(1) 若ax+b⩾f(x) 恒成立, f(x) 为上凸函数, 如下左图, 则x1⩽x2;(2) 若y=ax+b⩽f(x) 恒成立, f(x) 为下凸函数, 如下右图, 则x1⩾x2.由(1)或(2)得出x1,x2的大小,进而可以求得bk的最值.3. 赋值法对比不等式与目标式的结构, 发现当自变量取某个值时恰好构造出目标式.赋值法是零点比大小法方法的优化和改进,能快速解决线性表达式型、比值型的客观题. 点睛意领会“等比例赋值法”进行恰到好处的赋值.典型例题【例1】若(x2+x)ln 1x −ax⩽23x3+(1−a)x2−2ax+b 恒成立, 求b−2a 的最小值.【答案】−53【解析】解法1: 消元法设F(x)=23x3+(1−a)x2−2ax+b−(x2+x)ln 1x+ax ,则F′(x)=(2x+1)(ln x+x+令 ℎ(x)=ln x +x +1−a 得 ℎ(x) 单调递增, 故存在唯一 x 0 使得 ℎ(x 0)=0 , 即 a =x 0+ln x 0+1当 x ∈(0,x 0) 时, F(x) 单调递减当 x ∈(x 0,+∞) 时, F(x) 单调递增,故 F(x)min =F (x 0)=−13x 03−x 02−x 0+b.所以 F(x)min =F (x 0)⩾0, 即 b ⩾13x 03+x 02+x 0,b −2a ⩾13x 03+x 02−x 0−2ln x 0−2,t(x)=13x 3+x 2−x −2ln x −2,t ′(x)=(x−1)(x 2+3x+2)x,当 x ∈(0,1),t(x) 单调递减; 当 x ∈(1,+∞),t(x) 单调递增, 故 t(x)min =t(1)=−53. 所以 b −2a 的最小值为 −53.解法 2: :赋值法f(x)⩽g(x)⇔b −(x 2+x )a ⩾−(x 2+x )ln x −23x 3−x 2令 x 2+x =2 (等比例赋值法), 解得 x =1 (舍 x =−2 ), 则 b −2a ⩾−53.当 b −2a =−53 时, 由 f(x)−g(x)⩽0=f(1)−g(1) 知 x =1 是 f(x)−g(x) 的极值点,所以 f ′(1)−g ′(1)=0, 解得 a =2,b =73.下面证明: 当 a =2,b =73时, f(x)⩽g(x).证明:令 ℎ(x)=g(x)−f(x)=23x 3−x 2−2x +73+(x 2+x )ln x. 则 ℎ′(x)=(2x +1)(x −1+ln x),当 x >1 时, ℎ′(x)>0,ℎ(x) 递增; 当 0<x <1 时, ℎ′(x)<0,ℎ(x) 递减. 所以 ℎ(x)⩾ℎ(1)=0, 即 f(x)⩽g(x) 恒成立. 综上可知, b −2a 的最小值为 −53.【点睛】求线性表达式型 ma +nb(m,n 为常数) 的最值时, 赋值的要点在于把原不等式变 成关于 a,b 的二元一次不等式, 然后根据 a,b 的系数比与 m:n 相等求出 x 0 (简称等比例赋值法 ).【例2】若函数 f(x)=aln x +12x 2+2bx 在区间 [1,3] 上单调递增, 则 a +4b 的最小值为 . 【答案】 −4【解析】 g(x)=f ′(x)=ax +x +2b ⩾0 对 x ∈[1,3] 恒成立, 即 ax +2b +x ⩾0 对 x ∈[1,3] 恒成立, 与目标式 a +4b 比较, 令 1x :2=1:4, 得 x =2,因此令 x =2 (等比例赋值则 g(2)=a2+2+2b ⩾0⇒a +4b ⩾−4. ( a =1,b =−54时等号成立)所以 a +4b 的最小值为 −4.【点睛】这里用了等比【例】赋值法, 要点睛意等号成立的条件. 由已知得 ax +2b +x ⩾0 对 x ∈ [1,3] 恒成立, 与目标式 a +4b 比较, 令 1x :2=1:4 , 得 x =2 , 因此令 x =2 . 当 a +4b = −4 时, 由 g(x)⩾0=g(2) 知 x =2 是 g(x) 的极值点, 所以 g ′(2)=0⇒a =4,b =−2.比值型【例3】已知函数 f(x)=ln x +(e −a)x −2b, 若不等式 f(x)⩽0 对 x ∈(0,+∞) 恒成立, 则 ba 的最小值为 . 【答案】-12e.【解析】解法 1 : 消元法显然 a >e,f ′(x)=1x +(e −a), 易知 x =1a−e为 f(x) 的极大值点,所以只需 f (1a−e)⩽0, 即 2b ⩾−ln (a −e)−1, 所以 2b a⩾−ln (a−e)−1a.今े ℎ(a)=−12⋅[ln (a−e)+1]a,则 ℎ′(a)=−12⋅ea−e−ln (a−e)a 2, 点睛意到 ℎ′(2e)=0,易知 a =2e 为 ℎ(a) 的极小值点, ℎ(2e)=−12e .所以 ba ⩾−12e , 故 ba 的最小值为 −12e . 解法 2:零点比大小f(x)⩽0⇔ln x +(e −a)x −2b ⩽0⇔ln x +ex ⩽ax +2b, 即 ln x +ex ⩽a (x +2b a)函数 y =ln x +ex 与 y =a (x +2ba) 的零点分别为 1e ,−2b a由图可知: −2b a⩾1e⇒b a⩽−12e, 故 ba的最小值为 −12e.解法 3 : 赋值法f(x)⩽0⇔ln x +ex ⩽ax +2b, 令 x =1e, 则 a ⋅1e+2b ⩾0⇒b a⩾−12e.故 b a的最小值为 −12e.【点睛 1】求比值型的最值时, 赋值的要点在于把原不等式改写成一边只含有目标式分子、 分母的线性结构, 再令另一边为 0 , 找到 x 0.【点睛 2】观察不等式 ln x +ex ⩽ax +2b 与目标式 ba 的结构, 进行恰到好处的赋值. 只需 让 ln x +ex =0 , 便得 a ⋅1e +2b ⩾0 , 进而可求得 b a 的最值. 解方程 ln x +ex =0 , 可得 x =1e , 从而有上面的解法.【点睛 3】本题我们用了消元法、零点比大小和赋值法, 显然赋值法最为简捷. 【例4】已知不等式 (e −a)e x +x +b +1⩽0 恒成立, 其中 e 为自然常数, 则 b+1a的最大值 为 . 【答案】 1e【解析】赋值法(e −a)e x +x +b +1⩽0⇔ae x −(b +1)⩾e x+1+x , 令 e x+1+x =0 , 得 x =−1 , 则 a ⋅1e−(b +1)⩾0⇒b+1a⩽1e, 故 b+1a的最大值为 1e.乘积型【例5】 若 e x −x +12x 2⩾12x 2+ax +b 恒成立, 求 (a +1)b 的最大值. 【答案】 e2【解析】解法 1 : 消元法e x −x +12x 2⩾12x 2+ax +b ⇔e x −(a +1)x −b ⩾0,令 g(x)=e x −(a +1)x −b, 则 g ′(x)=e x −(a +1),(1)若 a +1<0, 则 g ′(x)>0, 则 g(x)=e x −(a +1)x −b 在 R 上单增, 当 x →−∞ 时, f(x)→−∞,与 g(x)⩾0 矛盾, 舍去. (2)若 a +1>0, 由 g ′(x)=0 得 x =ln (a +1),所以 g(x) 在 (−∞,ln (a +1)) 单减, 在 (ln (a +1),+∞) 单增, 则 g(x)min =g(ln (a +1))=(a +1)−(a +1)ln (a +1)−b ⩾0,即 b ⩽(a +1)−(a +1)ln (a +1) ， 则 b(a +1)⩽(a +1)2−(a +1)2ln (a +1)令 ℎ(t)=t 2−t 2ln t,t >0, 则 ℎ′(t)=t −2tln t =t(1−2ln t)所以ℎ(t) 在(0,√e) 单增, (√e,+∞) 单减, 所以ℎ(t)max=ℎ(√e)=e2, (3) 当a+1=0 时, (a+1)b=0,综上: (a+1)b 最大值为e2.解法2: 消元法e x−x+12x2⩾12x2+ax+b⇔e x−(a+1)x−b⩾0,即b⩽e x−(a+1)x(1)若a+1<0, 则(a+1)b⩾(a+1)e x−(a+1)2x,令ℎ(x)=(a+1)e x−(a+1)2x,ℎ′(x)=(a+1)e x−(a+1)2=(a+1)[e x−(a+1)]<0所以当x→−∞ 时, f(x)→+∞, 则(a+1)b⩾(a+1)e x−(a+1)2x 不成立(2) 若a+1>0, 则(a+1)b⩽(a+1)e x−(a+1)2x；令ℎ(x)=(a+1)e x−(a+1)2x,由ℎ′(x)=0 得x=ln (a+1), 则ℎ(x) 在(0,ln (a+1)) 单减, (ln (a+1),+∞) 单增,所以ℎ(x)=(a+1)2−(a+1)2ln (a+1),令g(t)=t2−t2ln t,t>0, 则g′(t)=t−2tln t=t(1−2ln t),所以g(t) 在(0,√e) 单增, (√e,+∞) 单减, 所以g(t)max=g(√e)=e2(3) 当a+1=0 时, (a+1)b=0,综上: (a+1)b 最大值为e2.【点睛】根据所求目标, 在a,b 都在变的情况下, 求(a+1)b 的最大值, 把b 移到一边, 同乘以(a+1), 构造出(a+1)b, 在等式的右边成功地消灭了变量b.【例6】已知函数f(x)=e x−xa −b ,当实数a>0 时, 对于x∈R 都有f(x)⩾0 恒成立, 则a2b 的最大值为（）A. −1e2B. 1e2C. −2e2D. 2e2【答案】A【解析】f′(x)=e x−1a , 易知x=ln 1a为极小值点, 则f(x)min=f(1a)=1a+ln aa−b⩾ 0 ,所以1a +ln aa⩾b ,则a2b⩽a+aln a ,令g(a)=a+aln a ,易得g(a)min=g(1e2)= −1e2.故a2b 的最大值为−1e2.强化训练1.已知不等式ln (x+1)−1⩽a(x+ba ) 对一切正数x 恒成立, 则ba的最小值为.【答案】1-e【解析】解法 1: 零点比大小ln (x +1)−1⩽a (x +ba) 恒成立,直线 y =a (x +ba ) 在函数 y =ln (x +1)−1 图象的上方, 直线 y =a (x +ba ) 在 x 轴上的截距为 −ba ,函数 y =ln (x +1)−1 在 (e −1,0) 处的切线为 y =1e [x −(e −1)],则 −b a ⩽e −1⇒b a ⩾1−e, 故 (ba )min=1−e解法 2 : 赋值法取 x =e −1,便有 ba ⩾1−e2.已知函数 f(x)=2ax 2+bx −3a +1,x ∈[−4,4] , 若 f(x)⩾0 恒成立, 则 5a +b 的取值 范围是当 5a +b 取得最小值时, a = . 【答案】 a =121【解析】赋值法2ax 2+bx −3a +1⩾0,x ∈[−4,4], 即 (2x 2−3)a +xb +1⩾0,x ∈[−4,4]. 令，解得或则由 f(3)⩾0, 得 5a +b ⩾−13; 由 f (−12)⩾0, 得 5a +b ⩽2.所以 5a +b 的取值范围是 [−13,2].当 5a +b =−13 时, f(x)⩾0=f(3), 可知 x =3 是函数 f(x) 的极值点 (或对称轴), 所以 −b4a =3, 易得 a =121. 3.已知不等式 x −3ln x +1⩾mln x +n(m ≠−3) 对 x >0 恒成立, 则 n−3m+3 的最大值为 .【答案】 −ln 2 【解析】赋值法，令，可得4.若对于任意正实数x, 都有ln x−aex−b+1⩽0 (e 为自然对数的底数) 成立, 则a+b 的最小值是.【答案】0【解析】令x=1e, 代入得: a+b⩾0,以下说明a+b=0 时满足条件,当a=1,b=−1 时, 令f(x)=ln x−ex+1+1=ln x−ex+2,则f′(x)=1x −e=1−exx, 令f′(x)=0, 解得: x=1e,可知当x∈(0,1e ) 时, f′(x)>0, 当x∈(1e,+∞) 时, f′(x)<0,故对任意正实数x, 都有f(x)⩽f(1e)=0,故a=1,b=−1 时, a+b=0, 满足题意, 故a+b 的最小值是0 ,故答案为: 0 .5.已知不等式e x⩾ax+b(a,b∈R, 且a≠0) 对任意实数x 恒成立, 则b−2a 的最大值为A. 2−ln 2B. 1−ln 2C. −2ln 2D. −ln 2【答案】D【解析】解法1:零点比大小由e x⩾ax+b 得e x−2⩾ax+(b−2)=a(x+b−2a),考虑y=e x−2 与y=a(x+b−2a) 在x 轴上的截距,只需−b−2a ⩾ln 2⇒b−2a⩽−ln 2.解法2 : 赋值法令e x−2=0 即x=ln 2, 结合a>0, 立得b−2a⩽−ln 2.6.已知函数f(x)=e x−12x2+x3, 若x∈R 时, 恒有f′(x)⩾3x2+ax+b, 则ab+b的最大值为（） A. √e B.√e 2C. e2D. e【答案】C【解析】因为函数 f(x)=e x −12x 2+x 3 , 则 f ′(x)=e x −x +3x 2 , 由题可知, 对 x ∈R ,恒 有 e x −x +3x 2⩾3x 2+ax +b ⇒e x −x −ax −b ⩾0 成立, 令 g(x)=e x −x −ax , 则 g ′(x)=e x −1−a 当 a <−1 时, 函数 g(x) 在 R 上单调递增, 且 x →−∞ 时, g(x)→−∞, 不符合题意;当 a =−1 时, ab +b =0, 当 a >−1 时, 令 g ′(x)=e x −1−a >0⇒x >ln (1+a), 所以函数 g(x) 在 (ln (1+a),+∞) 上单调递增, 且在 (−∞,ln (1+a)) 上单调递减; 所以 g(x)min =g[ln (1+a)]=e ln (1+a)−ln (1+a)−aln (1+a)=(1+a)− (1+a)ln (1+a),故 (1+a)−(1+a)ln (1+a)−b ⩾0⇒b(1+a)⩽(1+a)2−(1+a)2ln (1+a), 令 t =1+a >0, 则 ℎ(t)=t 2−t 2ln t, 且 ℎ′(t)=2t −(2tln t +t)=t(1−2ln t), 当 t ∈(0,√e) 时, ℎ′(t)>0, 函数 ℎ(t) 单调递增; 当 t ∈(√e,+∞) 时, ℎ′(t)<0, 函数 ℎ(t) 单调递减,所以 ℎ(t)max =ℎ(√e)=(√e)2−(√e)2ln √e =e2, 故 b(1+a)⩽e2, 综上所述, ab +b 的最大值为 e2.7.设函数 f(x)=ln (ax +b)−x(a,b ∈R), 若 f(x)⩽0 恒成立, 则 ab 的最大值为 .【答案】 e2【解析】 ln (ax +b)⩽x 恒成立, 即 e x ⩾ax +b >0 恒成立, a,x,b >0 e x ⩾ax +b ⩾2√ax ⋅b, 所以 ab ⩽e 2x 4x(x >0), 于是 ab ⩽(e 2x4x)min=e2.8.已知 a ≠0, 函数 y =f(x)=ae x ,y =g(x)=ealn x +b ( e 为自然对数的底数), 若存在一 条直线与曲线 y =f(x) 和 y =g(x) 均相切, 则 ba 最大值是 【答案】e【解析】 f ′(x)=ae x ,g ′(x)=ae x, 设切点分别为 (t,ae t ),(m,aelnm +b) , 则切线方程分别为 y −ae t =ae t (x −t);y −aelnm −b =ae m(x −m),由题意存在一条直线与曲线 y =f(x) 和 y =g(x) 均相切, 所以可得 ae m=ae t ,且 b =ae t (1−t)+ae −aelnm; 因为ae m=ae t , 且 a ≠0,=(1−t)e t+e−elnm=(1−t)e t−e(1−t)+e=e t+et−te t;所以ba令ℎ(t)=e t+et−te t, 则ℎ′(t)=−te t+e.当t=1 时, ℎ′(1)=0 ;当t<1 时, ℎ′(t)>0,ℎ(t) 单调递增; 当t>1 时, ℎ′(t)< 0,ℎ(t)单调递减;故当t=1 时取得最大值ℎ(1)=e.故答案为: e.切线放缩知识与方法1. 切线放缩对于含有指数、对数或三角函数等超越式的函数或不等式问题, 有时我们可以利用导数的几何意义进行以直代曲, 即考虑函数f(x) 图象上某点x=x0处的切线y=kx+b, 结合函数的凹凸性进行切线放缩, 使问题便于解决.特别地, 当f(x)⩾kx+b 为下凸函数时, 则f(x)⩾kx+b ;当f(x) 为上凸函数时, 则f(x)⩽kx+b. 两个不等式中等号成立的条件刚好是x=x0.将f(x) 放大或缩小为kx+b , 得到f(x)⩾kx+b 或f(x)⩽kx+b , (其中k= f′(x0),y =kx+b 为f(x) 在x=x0处的切线y=f′(x0)(x−x0)+f(x0)) 叫做切线放缩.对某些求函数的最小值或证明不等式的问题, 巧用切线放缩, 会有意想不到的效果.2. 常用的切线不等式(1) e x⩾x+1;(2)ln x⩽x−1;(3)e x⩾ex;(4)ln x⩽1x;(5)sin x⩽x(x⩾0).e【点睛】在 e x⩾x +1 中, 将 x 换成 ln x, 即得 x ⩾ln x +1⇒ln x ⩽x −1;在 e x ⩾x +1 中, 将 x 换成 x −1, 即得 e x−1⩾x ⇒e x ⩾ex; 在 e x ⩾ex 中, 将 x 换成 ln x, 即得 x ⩾elnx ⇔ln x ⩽1e x; 在 ln x ⩽x −1 中, 将 x 换成 x +1, 即得 ln (x +1)⩽x.典型例题逆用求导法则型【例1】若 x,y 是实数, e 是自然对数的底数, e x+y+2−3⩽ln (y −2x +1)+3x , 则2x +y = .【答案】- 83【解析】结合不等式 e x ⩾x +1 (当且仅当 x =0 时等号成立), 可得: e x+y+2⩾(x +y +2)+1=x +y +3 (1), 结合不等式 ln x ⩽x −1 (当且仅当 x =1 时等号成立),则 ln (y −2x +1)⩽(y −2x +1)−1, 所以 −ln (y −2x +1)⩾2x −y(1) (2) 两式相加, 即得: e x+y+2−ln (y −2x +1)⩾(x +y +3)+(2x −y)=3x +3 又已知 e x+y+2−3⩽ln (y −2x +1)+3x,所以 e x+y+2−3=ln (y −2x +1)+3x, 于是(1)与 (2) 中的等号同时成立, 所以 {x +y +2=0,y −2x +1=1, 解得 {x =−23,y =−43,所以 2x +y =−83. 故答案为: −83.【点睛】本题利用了夹逼法. 根据切线不等式 e x ⩾x +1 与 ln x ⩽x −1, 并结合已知条件,通过夹逼由不等式得到了方程, 最后点睛意到两个不等式中等号成立的条件, 解方程组即 可得到答案.【例2】已知函数 f(x)=ax +ln x +1, 若对任意的 x >0,f(x)⩽xe 2x 恒成立, 则求实数 a 的 取值范围是 . 【答案】 (−∞,2]【解析】解法 1: :切线放缩, 利用 e x ⩾x +1 对任意的 x >0,f(x)⩽xe 2x 恒成立, 等价于 a ⩽xe 2x −(ln x+1)x在 (0,+∞) 上恒成立.因为 xe 2x −(ln x +1)=e 2x+ln x −(ln x +1)⩾(2x +ln x +1)−(ln x +1)=2x, 所以 xe 2x −(ln x+1)x⩾2x x=2. 当且仅当 2x +ln x =0 时等号成立 (方程显然有解),即 (xe 2x −(ln x+1)x)min=2, 所以 a ⩽2.故答案为: (−∞,2]. 解法 2: 隐零点因为 f(x)=ax +ln x +1, 所以对任意的 x >0,f(x)⩽xe 2x 恒成立, 等价于 a ⩽e 2x −ln x+1x在 (0,+∞) 上恒成立.令 m(x)=e 2x −ln x+1x(x >0), 则只需 a ⩽m(x)min 即可, 则 m ′(x)=2x 2e 2x +ln xx 2,再令 g(x)=2x 2e 2x +ln x(x >0) , 则 g ′(x)=4(x 2+x )e 2x +1x>0 , 所以 g(x) 在(0,+∞)上单调递增, 因为 g (14)=√e 8−2ln 2<0,g(1)=2e 2>0,所以 g(x) 有唯一的零点 x 0, 且 14<x 0<1,所以当 0<x <x 0 时, m ′(x)<0, 当 x >x 0 时, m ′(x)>0, 所以 m(x) 在 (0,x 0) 上单调递减, 在 (x 0,+∞) 上单调递增,因为 2x 02e 2x 0+ln x 0=0, 所以 ln 2+2ln x 0+2x 0=ln(−ln x 0), 即 ln(2x 0)+2x 0=ln (−ln x 0)+(−ln x 0) ， 设 s(x)=ln x +x(x >0), 则 s ′(x)=1x +1>0, 所以函数 s(x) 在 (0,+∞) 上单调递 增,因为 s (2x 0)=s (−ln x 0), 所以 2x 0=−ln x 0, 即 e 2x 0=1x 0,2=−ln x 0x 0,所以 m(x)⩾m (x 0)=e 2x 0−ln x 0+1x 0=1x 0−ln x 0x 0−1x 0=2, 则有 a ⩽2,所以实数 a 的取值范围为 (−∞,2]. 故答案为: (−∞,2].【例3】已知 a 1,a 2,a 3,a 4 成等比数列, 且 a 1+a 2+a 3+a 4=ln(a 1+a 2+a 3), 若 a 1>1, 则（）A. a 1<a 3,a 2<a 4B. a 1>a 3,a 2<a 4C. a 1<a 3,a 2>a 4D. a 1>a 3,a 2>a 4 【答案】 B【解析】(利用 ln x ⩽x −1) 由 a 1+a 2+a 3+a 4=ln(a 1+a 2+a 3), 可得 a 1+a 2+a 3+a 4= ln(a 1+a 2+a 3)⩽a 1+a 2+a 3−1 , 所以 a 4⩽−1 , 故公比 q <0 . 若 q ⩽−1 , 则 a 1+a 2+a 3 +a 4=a 1(1+q)(1+q 2)⩽0 , 而 a 1+a 2+a 3=a 1(1+q +q 2)⩾a 1>1 ,即 ln(a 1+a 2+a 3)>0 , 矛盾; 所以 −1<q <0 , 所以 a 1−a 3=a 1(1−q 2)>0,a 2−a 4= a 1q (1−q 2)<0, 所以 a 1>a 3,a 2<a 4, 故选 B.多变量轮换式的切线放缩【例4】f(x)=3+x1+x 2,x ∈[0,3], 已知数列 {a n } 满足 0<a n ⩽3,n ∈N ∗, 且满足 a 1+a 2+⋯ +a 2010=670, 则 f (a 1)+f (a 2)+⋯+f (a 2010)= A. 有最大值 6030 B. 有最大值 6027 C. 有最小值 6027 D. 有最小值 6030 【答案】A【解析】由 f(x)=3+x1+x 2(0⩽x ⩽3) , 得 f ′(x)=−x 2−6x+1(1+x 2)2, 所以 f ′(13)=−910,f(x) 在x =13 处的切线方程为 y =−910x +3310 , 下证 f(x)=3+x 1+x 2⩽310(11−3x) . 而 f(x)=3+x 1+x 2⩽310(11−3x)⇔(x −3)(x −13)2⩽0.因为 x ∈[0,3], 所以 (x −3)(x −13)2⩽0 成立, 故 f(x)=3+x1+x 2⩽310(11−3x).所以当 0<a n ⩽3,n ∈N ∗ 时, 有 f (a n )⩽310(11−3a n ),f (a 1)+f (a 2)+⋯+f (a 2010)⩽310[11×2010−3(a 1+a 2+⋯+a 2010)]=6030.故 f (a 1)+f (a 2)+⋯+f (a 2010) 最大值 6030 . 【点睛】本题利用函数 f(x)=3+x 1+x 2在 x =13处的切线进行放缩, 思路如下: 点睛意到a 1+ a 2+⋯+a 2010=670 , 当 a 1=a 2=⋯=a 2010 时, 有 a 1=a 2=⋯=a 2010=13 , 即 13是各元相 等时候的平衡点, 于是求出函数在平衡点的切线方程 y =−910x +3310, 可得 f(x)⩽310(11−3x).双参数最值的切线放缩【例5】已知不等式ln (x+1)−1⩽a(x+ba ) 对一切正数x 恒成立, 则ba的最小值为【解析】ln (x+1)−1⩽a(x+ba ) 恒成立,直线y=a(x+ba) 在函数y=ln (x+1)−1图象的上方,直线y=a(x+ba ) 在x 轴上的截距为−ba,函数y=ln (x+1)−1 在(e−1,0) 处的切线为y=1e[x−(e−1)],则−ba ⩽e−1⇒ba⩾1−e, 故(ba)min=1−e【点睛】本题利用两函数的零点比较大小, 其实就是切线放缩.强化训练1.已知函数f(x)=e x−1,g(x)=ln (x+1), 直线l 与y=f(x) 的图象相切, 与y= g(x) 的图象也相切, 则直线的l 方程是.【答案】y=x【解析】f(x)=e x−1 与g(x)=ln (x+1) 互为反函数, 其图象如图,其公共点为O(0,0),由f(x)=e x−1, 得f′(x)=e x, 所以f′(0)=1,曲线f(x)=e x−1 在O(0,0) 处的切线方程为y=x,由g(x)=ln (x+1), 得g′(x)=1x+1, 所以g′(0)=1,曲线g(x)=ln (x+1) 在O(0,0) 处的切线方程为y=x,所以曲线f(x)=e x−1 与曲线g(x)=ln (x+1) 的公切线为y=x.故答案为: y=x.2.已知实数a,b,c 满足e a+c+e2b−c−1⩽a+2b+1 (e 为自然对数的底数), 则a2+b2的最小值是.【答案】15【解析】设u(x)=e x−(x+1), 则u′(x)=e x−1, 可知u(x)⩾u(0)=0, 即e x⩾x+1;由不等式性质可知e a+c+e2b−c−1⩾a+c+1+2b−c=a+2b+1 ,当且仅当a+c= 2b−c−1=0 时取等号;又因为e a+c+e2b−c−1⩽a+2b+1,即有: e a+c+e2b−c−1=a+c+1,所以a+c=2b−c−1=0; 即a=−c,b=c+12;所以a2+b2=c2+(c+1)24=54c2+c2+14=54(c+15)2+15⩾15当且仅当c=−15时取等号, 故a2+b2的最小值是15, 答案为:15.3.函数f(x)=e x−a+x,g(x)=ln (x+2)−4e a−x, 若∃x0使得f(x0)−g(x0)=3, 则a= .【答案】-1- ln 2【解析】令f(x)−g(x)=x+e x−a−1n(x+2)+4e a−x,令y=x−ln (x+2),y′=1−1x+2=x+1x+2,故y=x−ln (x+2) 在(−2,−1) 上是减函数(−1,+∞) 上是增函数,故当x=−1 时, y 有最小值−1−0=−1,而e x−a+4e a−x⩾4. ( 当且仅当e x−a=4e a−x, 即x=ln 2+a 时, 等号成立);。

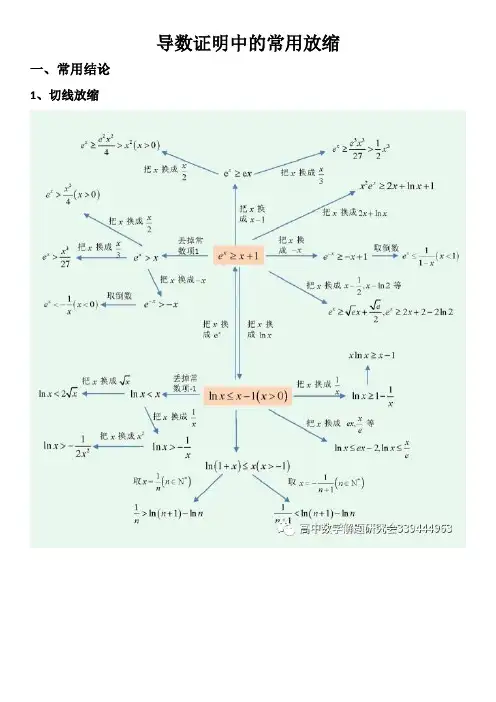
导数证明中的常用放缩一、常用结论1、切线放缩2、其它对数放缩（对数均值不等式）3、常用放缩公式：（考试时需给出证明过程）第一组：对数放缩（放缩成一次函数）ln 1x x ≤-，ln x x <，()ln 1x x +≤ （放缩成双撇函数）()11ln 12x x x x ⎛⎫<-> ⎪⎝⎭，()11ln 012x x x x ⎛⎫>-<< ⎪⎝⎭， )ln 1x x<>，)ln 01x x ><<， （放缩成二次函数）2ln x x x ≤-，()()21ln 1102x x x x +≤--<<，()()21ln 102x x x x +≥-> （放缩成类反比例函数）1ln 1x x≥-，()()21ln 11x x x x ->>+，()()21ln 011x x x x -<<<+，()ln 11x x x +≥+，()()2ln 101x x x x +>>+，()()2ln 101x x x x+<<+ 第二组：指数放缩（放缩成一次函数）1x e x ≥+，x e x >，x e ex ≥， （放缩成类反比例函数）()101x e x x ≤≤-，()10x e x x<-<， （放缩成二次函数）()21102x e x x x ≥++>，2311126x e x x x ≥+++， 第三组：指对放缩()()ln 112x e x x x -≥+--=第四组：三角函数放缩()sin tan 0x x x x <<>，21sin 2x x x ≥-，22111cos 1sin 22x x x -≤≤-. 第五组：以直线1y x =-为切线的函数ln y x =，11x y e -=-，2y x x =-，11y x=-，ln y x x =.二、基础练习：练习题组一练习题组二：二、经典例题：母题 (2017·全国Ⅲ)已知函数f (x )＝ln x ＋ax 2＋(2a ＋1)x .(1)讨论f (x )的单调性；(2)当a <0时，证明f (x )≤－34a－2.(1)解 f (x )的定义域为(0，＋∞)，f ′(x )＝1x ＋2ax ＋2a ＋1＝(x ＋1)(2ax ＋1)x. 若a ≥0，则当x ∈(0，＋∞)时，f ′(x )>0，故f (x )在(0，＋∞)上单调递增．若a <0，则当x ∈⎝⎛⎭⎫0，－12a 时，f ′(x )>0； 当x ∈⎝⎛⎭⎫－12a ，＋∞时，f ′(x )<0. 故f (x )在⎝⎛⎭⎫0，－12a 上单调递增，在⎝⎛⎭⎫－12a ，＋∞上单调递减． (2)证明 由(1)知，当a <0时，f (x )在x ＝－12a 处取得最大值，最大值为f ⎝⎛⎭⎫－12a ＝ln ⎝⎛⎭⎫－12a －1－14a， 所以f (x )≤－34a －2等价于ln ⎝⎛⎭⎫－12a －1－14a ≤－34a－2， 即ln ⎝⎛⎭⎫－12a ＋12a＋1≤0. 设g (x )＝ln x －x ＋1，则g ′(x )＝1x－1. 当x ∈(0,1)时，g ′(x )>0；当x ∈(1，＋∞)时，g ′(x )<0.所以g (x )在(0,1)上单调递增，在(1，＋∞)上单调递减．故当x ＝1时，g (x )取得最大值，最大值为g (1)＝0.所以当x >0时，g (x )≤0.从而当a <0时，ln ⎝⎛⎭⎫－12a ＋12a ＋1≤0，即f (x )≤－34a－2. [子题1] 设函数f (x )＝ln x －x ＋1.证明：当x ∈(1，＋∞)时，1<x －1ln x<x . 证明 f ′(x )＝1x －1＝1－x x，x >0， 当x >1时，f ′(x )<0，f (x )单调递减，当0<x <1时，f ′(x )>0，f (x )单调递增，∴f (x )＝ln x －x ＋1≤f (1)＝0，∴ln x ≤x －1，∴当x >1时，ln x <x －1，①且ln 1x <1x－1，② 由①得，1<x －1ln x ，由②得，－ln x <1－x x， ∴ln x >x －1x ，∴x >x －1ln x， 综上所述，当x >1时，1<x －1ln x<x . [子题2] 已知函数f (x )＝e x －x 2.求证：当x >0时，e x ＋(2－e )x －1x≥ln x ＋1. 证明 设g (x )＝f (x )－(e －2)x －1＝e x －x 2－(e －2)x －1(x >0)，则g ′(x )＝e x －2x －(e －2)，设m (x )＝e x －2x －(e －2)(x >0)，则m ′(x )＝e x －2，易得g ′(x )在(0，ln 2)上单调递减，在(ln 2，＋∞)上单调递增，又g ′(0)＝3－e>0，g ′(1)＝0，由0<ln 2<1，则g ′(ln 2)<0，所以存在x 0∈(0，ln 2)，使得g ′(x 0)＝0，所以当x ∈(0，x 0)∪(1，＋∞)时，g ′(x )>0；当x ∈(x 0,1)时，g ′(x )<0.故g (x )在(0，x 0)上单调递增，在(x 0,1)上单调递减，在(1，＋∞)上单调递增，又g (0)＝g (1)＝0，所以g (x )＝e x －x 2－(e －2)x －1≥0，故当x >0时，e x ＋(2－e )x －1x≥x . 又由母题可得ln x ≤x －1，即x ≥ln x ＋1，故e x ＋(2－e )x －1x≥ln x ＋1. 规律方法 利用导数证明不等式f (x )>g (x )的基本方法(1)若f (x )与g (x )的最值易求出，可直接转化为证明f (x )min >g (x )max .(2)若f (x )与g (x )的最值不易求出，可构造函数h (x )＝f (x )－g (x )，然后根据函数h (x )的单调性或最值，证明h (x )>0.(3)通过题目中已有的或常用的不等式进行证明．(4)利用赋值法证明与正整数有关的不等式.跟踪演练1．(2018·全国Ⅰ)已知函数f (x )＝a e x －ln x －1.(1)设x ＝2是f (x )的极值点，求a ，并求f (x )的单调区间；(2)证明：当a ≥1e时，f (x )≥0. (1)解 f (x )的定义域为(0，＋∞)，f ′(x )＝a e x －1x. 由题设知，f ′(2)＝0，所以a ＝12e 2. 从而f (x )＝12e 2e x －ln x －1，f ′(x )＝12e 2e x －1x. 当0<x <2时，f ′(x )<0；当x >2时，f ′(x )>0.所以f (x )的单调递增区间为(2，＋∞)，单调递减区间为(0,2)．(2)证明 当a ≥1e 时，f (x )≥e x e－ln x －1. 设g (x )＝e x e－ln x －1(x ∈(0，＋∞))， 则g ′(x )＝e x e －1x. 当0<x <1时，g ′(x )<0；当x >1时，g ′(x )>0.所以x ＝1是g (x )的最小值点．故当x >0时，g (x )≥g (1)＝0.因此，当a ≥1e时，f (x )≥0. 2．(2020·北京市陈经纶中学模拟)已知函数f (x )＝ln x －1x－ax .若1<a <2，求证：f (x )<－1. 证明 f (x )的定义域为(0，＋∞)，为了证明f (x )<－1，即ln x －1x－ax <－1， 只需证明ln x －1－ax 2<－x ，即ln x <ax 2－x ＋1，令m (x )＝ln x －x ＋1(x >0)，则m ′(x )＝1x－1， 令m ′(x )>0，得0<x <1；令m ′(x )<0，得x >1，所以m (x )在(0,1)上单调递增，在(1，＋∞)上单调递减，所以m (x )max ＝m (1)＝0，即ln x －x ＋1≤0，则ln x ≤x －1.令n (x )＝ax 2－2x ＋2，因为1<a <2，所以Δ＝4－8a <0，所以n (x )>0恒成立，即ax 2－2x ＋2>0，所以ax 2－x ＋1>x －1.综上所述，ln x <ax 2－x ＋1，即当1<a <2时，f (x )<－1.（2017年全国新课标1·理·21）已知()()22x x f x ae a e x =+--.（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围.解析：（1）()()()()2'221211x x x x f x ae a e e ae =+--=+-若0a ≤，则()'0f x <恒成立，所以()f x 在R 上递减；若0a >，令()'0f x =，得11,ln x e x a a ==. 当1ln x a <时，()'0f x <，所以()f x 在1,ln a ⎛⎫-∞ ⎪⎝⎭上递减； 当1lnx a >时，()'0f x >，所以()f x 在1ln ,a ⎛⎫+∞ ⎪⎝⎭上递增. 综上，当0a ≤时，()f x 在R 上递减；当0a >时，()f x 在1,ln a ⎛⎫-∞ ⎪⎝⎭上递减，在1ln ,a ⎛⎫+∞ ⎪⎝⎭上递增. （2）()f x 有两个零点，必须满足()min 0f x <，即0a >，且()min 111ln1ln 0f x f a a a ⎛⎫==--< ⎪⎝⎭. 构造函数()1ln g x x x =--，0x >. 易得()1'10g x x =--<，所以()1ln g x x x =--单调递减. 又因为()10g =，所以()11111ln 01101g g a a a a a ⎛⎫--<⇔<⇔>⇔<< ⎪⎝⎭. 下面只要证明当01a <<时，()f x 有两个零点即可，为此我们先证明当0x >时，ln x x >. 事实上，构造函数()ln h x x x =-，易得()1'1h x x=-，∴()()min 11h x h ==，所以()0h x >，即ln x x >. 当01a <<时，()()22222110a ea e a a f e e e++---=++=>， ()2333333ln 121ln 11ln 10a f a a a a a a a a -⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+----=---> ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭， 其中11ln a -<，31ln ln a a a ->，所以()f x 在11,ln a ⎛⎫- ⎪⎝⎭和13ln ,ln a a a -⎛⎫ ⎪⎝⎭上各有一个零点. 故a 的取值范围是()0,1.注意：取点过程用到了常用放缩技巧。

所 以 G(x) 在 ( － ∞ ， 0) 上 单 调 递 减 ， 在 (0 ， ＋ ∞) 上 单 调 递 增 ， 所 以 G(x)≥G(0)＝0， 所以f(x)≥t(x)恒成立，所以f(x2)≥t(x2)， 设t(x)＝m的根为x4，则x4＝m， 又函数t(x)单调递增， 且m＝t(x4)＝f(x2)≥t(x2)，所以x4≥x2， 所以 x2－x1≤x4－x3＝m－－1＋1e－me
则 F′(x)＝(x＋2)ex－1e， 令 m(x)＝F′(x)＝(x＋2)ex－1e， 则m′(x)＝(x＋3)ex， 所以当x<－3时，m′(x)<0； 当x>－3时，m′(x)>0， 所以F′(x)在(－∞，－3)上单调递减， 在(－3，＋∞)上单调递增，
当 x→－∞时，F′(x)→－1e，又 F′(－1)＝0， 所以当x<－1时，F′(x)<0，F(x)单调递减； 当x>－1时，F′(x)>0，F(x)单调递增， 所以F(x)≥F(－1)＝0，所以f(x)≥h(x)恒成立，则f(x1)≥h(x1)， 设 h(x)＝m 的根为 x3，则 x3＝－1＋1e－me， 又h(x)单调递减， 且m＝h(x3)＝f(x1)≥h(x1)，
培优点1 专题一 函数与导数 切线放缩
专题一 函数与导数
在高考压轴题中，经常考查与导数有关的不等式问题，这些问题可以用 常规方法求解，也可以用切线不等式进行放缩.导数切线放缩法是一种非常实 用的数学方法，它可以帮助我们更好地理解函数的性质和变化规律，更能使 问题简单化，利用切线不等式进行求解，能起到事半功倍的效果.
规 该方法适用于凹函数与凸函数且它们的凹凸性相反的问题(拆成两
律
方 个函数)，两函数有斜率相同的切线，这是切线放缩的基础，引入 法 一个中间量，分别证明两个不等式成立，然后利用不等式的传递

如图所示，又点 Q a,2 a 到直线 x 0 的距离为 a ，
自然想到转化为动点 Q 到抛物线准线 x 1 的距离，
结合抛物线的概念可得 D
x a2
ex 2
a
2
a 2
PQ QH 1 PQ QF 1 ，所以 D PQ QF 1 PF 1 ，当且仅当 P,Q, F 共线，
bn
1
n n 1
，
-2-
慧学上进
所以只需证明
an
n
1
1 n
2
ln2
n 1 n
bn
n
1
n 1
.
由（1）知 a 1 时，有 x ln x x 1 ，即 ln x x 1 . x
令
x
n
n
1
1
，则
ln
n
n
1
n
1
1
，
所以
ln2
n 1 n
n
1
12
n
1
1 n
2
1 n 1
n
1
2
，
所以 ln2 2 ln2 3 ln2 n 1 1 1 n ；
命题角度 1 构造函数
【典例1】（赣州市2018届高三摸底考试）已知函数
f
x 1
ln x , g(x) x
ae ex
1 x
bx
，若曲线
y
f
x 与曲
线 y g x 的一个公共点是 A1,1 ，且在点 A 处的切线互相垂直．
（1）求 a,b 的值；
（2）证明：当 x 1 时， f x g(x) 2 ．
缩法进行放缩解决问题.
命题角度 4 二元或多元不等式的解证思路 【典例 6】（皖南八校 2018 届高三第三次联考）若 x, a,b 均为任意实数，且 a 22 b 32 1 ，则

高考数学助手：导数中证明不等式技巧构造切线放缩二元变量凹凸反转
导数中不等式的证明是历年的高考中一个永恒的话题，由于不等式证明的灵活性，多样性，该考点也备受命题者的青睐。

今天将会通过五个方面系统的介绍一些常规的不等式的证明手段。

总的来说：
命题角度1 构造函数
命题角度2 放缩法
命题角度3 切线法
命题角度4 二元或多元不等式的证明思路
命题角度5 函数凹凸性的应用
这五种命题角度，五种解题方法，同学们一定要会呢！导数在高考中占的比重还是挺大的！。

函数凸凹性在高考解题中的应用一隅函数凸凹性是高等数学研究的函数重要性质之一,虽然在高中数学的课标中没有对凸凹函数做具体要求,但是它的身影在高考试题中却频频出现. 充分说明了高考命题源于课本，又高于课本的原则，同时也体现了高考为高校输送优秀人才的选拔性功能.下面仅就函数凸凹性的一个侧面在高考题中的应用做初步论述.一、凹凸函数的定义及相关定理定义：如果函数()f x 对其定义域中任意的1x ，2x 都有如下不等式 [])()(21)2(2121x f x f x x f +≤+ （1） 成立，则称)(x f 是下凸（凸）函数(如图1所示)，当且仅当21x x =时等号成立． 如果函数()f x 对其定义域中任意的1x ，2x 都有如下不等式[])()(21)2(2121x f x f x x f +≥+ （2） 成立，则称)(x f 是上凸（凹）函数(如图2所示)，当且仅当21x x =时等号成立．从几何意义来看，不等式（1）表示定义域中任意两点1x ，2x 的中点M 所对应的曲线上的点Q 位于弦上对应点P 的下面．不等式（2）则有相反的意义．引理：设函数)(x f 在开区间I 上可导，则(1))(x f 在区间I 上为上凸函数⇔导函数)(x f '在区间I 单调减少．()0<''⇔x f(2))(x f 在区间I 上为下凸函数⇔导函数)(x f '在区间I 单调增加．()0>''⇔x f 定理：若函数)(x f 在开区间),(b a 上为下凸函数且可导，),(00y x P 为其图像上一点，则函数)(x f 的图像必在P 点处函数切线的上方；反之，若函数)(x f 在开区间),(b a 上为上凸函数且可导，则函数)(x f 的图像必在P 点处函数切线的下方.证明:由函数)(x f 在开区间I 上可导,从而P 点处函数切线方程为000))((y x x x f y +-'=记000))(()()(y x x x f x f x F --'-=,)()()(0x f x f x F '-'='当)(x f 在开区间),(b a 上为下凸函数时,由引理得)(x F 在0x x =处取得最小值0,即,0)(≥x F 也即000))(()(y x x x f x f +-'≥,∴即证函数)(x f 的图像在P 点处函数切线的上方;同理可得,若函数)(x f 在开区间),(b a 上为上凸函数且可导，则函数)(x f 的图像必在P 点处函数切线的下方.二、定理在高考题中的应用以下就2012年高考试题中出现的若干有关凸凹性的试题来说明定理的解题应用价值. 例1.(新课标•理21) 已知函数()f x 满足满足121()(1)(0)2x f x f ef x x -'=-+； （1）求()f x 的解析式及单调区间；（2）若21()2f x x ax b ≥++，求(1)a b +的最大值。

高考数学复习考点题型专题讲解专题41 切割线放缩1.切线放缩若函数y＝f(x)在区间[a，b]上有凹凸性，可以利用切线y＝f′(x0)(x－x0)＋f(x0)进行放缩.(1)若函数y＝f(x)在[a，b]上的图形是凹的(f″(x)>0)，则有f(x)≥f′(x0)(x－x0)＋f(x)；(2)若函数y＝f(x)在[a，b]上的图形是凸的(f″(x)<0)，则有f(x) ≤f′(x0)(x－x0)＋f(x0).2.割线放缩若函数y＝f(x)在区间[a，b]上有凹凸性，可以利用割线y＝f（b）－f（a）b－a(x－a)＋f(a)进行放缩.(1)若函数y＝f(x)在[a，b]上的图形是凹的(f″(x)>0)，则有f(x)≤f（b）－f（a）b－a(x－a)＋f(a).(2)若函数y＝f(x)在[a，b]上的图形是凸的(f″(x)<0)，则有f(x)≥f（b）－f（a）b－a(x－a)＋f(a). 如图类型一切线放缩1.切线放缩证明不等式的原理：f(x)≥(≤)l切≥(≤)g(x).2.利用切线放缩求参数范围：分离参数需找到所设函数的极值点范围后运用切线放缩. 例1 若e x－2x ln x－kx－1≥0对任意实数x>0都成立，求k的取值范围.解由e x－2x ln x－kx－1≥0，得k≤e x－1x－2ln x，设μ(x)＝e x－1x－2ln x，μ′(x)＝1＋e x（x－1）－2xx2，令μ′(x)＝0，得1＋e x(x－1)－2x＝0，∴e x－2－1x－1＝0，记φ(x)＝e x－2－1x－1，则x>1时φ(x)单调递增，x→1时，φ(x)<0，x＝2时，φ(x)>0. 设其根为x0，则x0∈(1，2)，所以μ(x)的极值点在x＝1附近.因此考虑在x＝1处进行切线放缩，而y＝e x－1x在x＝1处的切线为y ＝x ＋e －2，所以有e x－1x≥x ＋e －2，即μ(x )≥x ＋e －2－2ln x .设h (x )＝x －2ln x ＋e －2，h ′(x )＝1－2x，可得h (x )在x ＝2处取最小值，h (2)＝e －2ln 2，即k ≤e－2ln 2. ∴k 的取值范围为(－∞，e －2ln 2]. 训练1 已知f (x )＝e x ＋cos 2x ＋2x 2＋x －2. (1)求f (x )在x ＝0处的切线； (2)求证：f (x )≥ln(2x ＋1).(1)解 由题意知f ′(x )＝e x －2sin 2x ＋4x ＋1，则f ′(0)＝2，而f (0)＝0， 所以f (x )在x ＝0处的切线方程为y －0＝2(x －0)，即y ＝2x .(2)证明 先证f (x )≥2x ，令g (x )＝f (x )－2x ＝e x ＋cos 2x ＋2x 2－x －2， 则g ′(x )＝e x －2sin 2x ＋4x －1，g ″(x )＝e x －4cos 2x ＋4>0恒成立， ∴g ′(x )单调递增，又g ′(0)＝0， 易知g (x )≥g (0)＝0，∴f (x )≥2x . 再证2x ≥ln(2x ＋1)，令h (x )＝2x －ln(2x ＋1)⎝⎛⎭⎪⎫x >－12，h ′(x )＝2－22x ＋1＝4x2x ＋1，令h ′(x )＝0，解得x ＝0. 当x >0时，h ′(x )>0，则h (x )在(0，＋∞)上单调递增； 当－12<x <0时，h ′(x )<0，则h (x )在⎝ ⎛⎭⎪⎫－12，0上单调递减，所以h (x )≥h (0)＝0，即2x≥ln(2x＋1)，综上f(x)≥ln(2x＋1).类型二切线类的应用1.一般地，给出函数的表达式，证明关于函数零点差的不等式(无等号)，可以考虑切线类技巧来解决.2.切线类的本质是把两零点利用切线的零点来放缩不等式.3.注意数形结合思想的应用.例2(2022·泰安联考)已知函数f(x)＝(x－1)ln(x＋1)，曲线y＝f(x)在点(1，0)处的切线方程为y＝kx＋b.(1)求k，b的值；(2)证明：f(x)≥kx＋b；(3)若函数g(x)＝f(x)＋m(m∈R)有两个零点x1，x2，证明：|x1－x2|≤1－m－mln 2.(1)解函数f(x)的定义域为(－1，＋∞)，f′(x)＝ln(x＋1)＋x－1 x＋1，f′(1)＝ln 2.所以切线方程为y＝ln 2·(x－1)，即k＝ln 2，b＝－ln 2.(2)证明设h(x)＝f(x)－kx－b＝(x－1)ln(x＋1)－x ln 2＋ln 2，h′(x)＝ln(x＋1)－2x＋1＋1－ln 2.令F(x)＝h′(x)＝ln(x＋1)－2x＋1＋1－ln 2，则F′(x)＝1x＋1＋2（x＋1）2>0，所以F(x)单调递增，即h′(x)单调递增.又h′(1)＝ln 2－1＋1－ln 2＝0，所以当x∈(－1，1)时，h′(x)<0，函数h(x)单调递减；当x∈(1，＋∞)时，h′(x)>0，函数h(x)单调递增，所以h(x)min＝h(1)＝0，即h(x)≥0，所以f(x)≥x ln 2－ln 2.(3)证明g(x)＝f(x)＋m(m∈R)的两个零点x1，x2，即为f(x)＝－m的两根，不妨设x1<x2，由题知，曲线y＝f(x)在(1，0)处的切线方程为y＝x ln 2－ln 2，令h(x)＝x ln 2－ln 2，即h(x)＋m＝0，即h(x)＝－m的根为x2′，则x2′＝1－mln 2，由(2)知，f(x2)≥h(x2)，∴h(x2′)＝f(x2)≥h(x2)，∵h(x)单调递增，∴x2′≥x2.设曲线y＝f(x)在(0，0)处的切线方程为y＝t(x)，∵f′(0)＝－1，∴t(x)＝－x，设方程t(x)＋m＝0，即t(x)＝－m的根为x1′，则x1′＝m，令T(x)＝f(x)－t(x)，同理由(2)可得T (x )≥0，即f (x )≥t (x )，f (x 1)≥h (x 1)，∴h (x 1′)＝f (x 1)≥h (x 1)， 又f (x )单调递减， ∴x 1′<x 1，∴|x 2－x 1|＝x 2－x 1≤x 2′－x 1′ ＝1－m －m ln 2.训练2 已知函数f (x )＝(x ＋1)(e x －1)，若方程f (x )＝m 有两个实根x 1，x 2，且x 1<x 2，证明：x 2－x 1≤1＋m （1－2e ）1－e.证明 如图，设f (x )在(－1，0)处的切线方程为y ＝h (x )，由f ′(x )＝(x ＋2)e x －1，易得，h (x )＝⎝ ⎛⎭⎪⎫1e －1(x ＋1)，令F (x )＝f (x )－h (x )，即F (x )＝(x ＋1)(e x－1)－⎝ ⎛⎭⎪⎫1e －1(x ＋1)，F ′(x )＝(x ＋2)e x －1e， 当x ≤－2时，F ′(x )＝(x ＋2)e x －1e ≤－1e<0，当x >－2时，则F ′(x )＝(x ＋2)e x－1e单调递增，又F ′(－1)＝0，所以当x <－1时，F ′(x )<0，当x >－1时，F ′(x )>0，所以函数F (x )在区间(－∞，－1)上单调递减，在区间(－1，＋∞)上单调递增， 故F (x )≥F (－1)＝0，f (x 1)≥h (x 1)， 设h (x )＝m 的根为x 1′，则x 1′＝－1＋m e 1－e，且h (x 1′)＝f (x 1)≥h (x 1)，又函数h (x )单调递减，故x 1′≤x 1，又设f (x )在(0，0)处的切线方程为φ(x )，易得φ(x )＝x . 令g (x )＝(x ＋1)(e x －1)－x ，g ′(x )＝(x ＋2)e x －2， 当x ≤－2时，g ′(x )＝(x ＋2)e x －2≤－2<0，当x >－2时，g ′(x )＝(x ＋2)e x －2单调递增，又g ′(0)＝0， 所以当x <0时，g ′(x )<0，当x >0时，g ′(x )>0，所以函数g (x )在区间(－∞，0)上单调递减，在区间(0，＋∞)上单调递增， 故g (x )≥g (0)＝0，即(x ＋1)(e x －1)≥x ，故f (x )≥φ(x )，则f (x 2)≥φ(x 2)， 设φ(x )＝m 的根为x 2′，则x 2′＝m ，且φ(x 2′)＝f (x 2)≥φ(x 2)， 又函数φ(x )单调递增，故x 2′≥x 2，又x 1′≤x 1，x 2－x 1≤x 2′－x 1′≤m －⎝ ⎛⎭⎪⎫－1＋m e 1－e ＝1＋m （1－2e ）1－e .类型三 割线放缩及割线类1.割线放缩关键是根据不等式的特点和需要，找准相关的函数及其割线，才能恰当的割线放缩.2.割线类本质与切线类类似.例3 已知x ∈⎝ ⎛⎭⎪⎫0，π2，求证：cos x ＋tan x >2x . 证明 先证∀x ∈⎝ ⎛⎦⎥⎤0，π4，sin x ＋tan x >2x ，设f (x )＝sin x ＋tan x －2x ，0<x ≤π4，f ′(x )＝（cos x －1）（cos 2x －cos x －1）cos 2x >0，f (x )在⎝⎛⎦⎥⎤0，π4上单调递增，f (x )>f (0)＝0，∴sin x ＋tan x >2x ⎝⎛⎭⎪⎫0<x ≤π4.于是当x ∈⎝ ⎛⎦⎥⎤0，π4时，有cos x ＋tan x ≥sin x ＋tan x >2x ， 当x ∈⎝ ⎛⎭⎪⎫π4，π2时，利用y ＝cos x 在x ＝π4和x ＝π2之间的割线，有cos x >－22π⎝ ⎛⎭⎪⎫x －π2， 利用y ＝tan x 在x ＝π4处的展开，有tan x >1＋2⎝ ⎛⎭⎪⎫x －π4＋2⎝⎛⎭⎪⎫x －π42，于是当x ∈⎝ ⎛⎭⎪⎫π4，π2时，有cos x ＋tan x －2x >1＋2－π2＋π28－⎝ ⎛⎭⎪⎫22π＋πx ＋2x 2， 右侧对应的Δ＝8π2＋4π－42－8<0，∴cos x ＋tan x －2x >0恒成立. 综上所述cos x ＋tan x >2x .训练3 已知函数f (x )＝x ln x ，若方程f (x )＝m 有2个根x 1，x 2(x 2>x 1)，求证：x 2－x 1>1＋e m .证明 (割线类)f ′(x )＝1＋ln x ，f (x )在⎝ ⎛⎭⎪⎫0，1e 上单调递减，在⎝ ⎛⎭⎪⎫1e ，＋∞上单调递增，所以f (x )min ＝f ⎝ ⎛⎭⎪⎫1e ＝－1e .又当0<x <1时，f (x )<0，x >1时，f (x )>0，∴－1e <m <0时，f (x )＝m 有2个不等的根x 1，x 2(x 2>x 1).当x ∈⎝⎛⎭⎪⎫0，1e 时，可证得：f (x )<－x ，故y ＝m 时，x 1<－m ；当x ∈⎝ ⎛⎭⎪⎫1e ，1时，可证得：x －1e －1>f (x )，故y ＝m 时，x 2>1＋(e －1)m ，∴x 2－x 1>1＋e m .一、基本技能练1.已知x ∈(0，e)，求证：（e 2－e 2ln x ＋x ）2ln 2x ＋2ln x ＋2>e 25.证明 原式等价于(e ln x －1－e(ln x －1))2>15(ln 2x ＋2ln x ＋2).令t ＝ln x －1(t <0)， 即证：(e t －e t )2>15t 2＋45t ＋1，取y ＝e t －e t 在t ＝0处的切线，有e t －e t >(1－e)t ＋1，t <0， (e t －e t )2>[(1－e)t ＋1]2＝(e －1)2t 2－2(e －1)t ＋1，当t<0时，有(e－1)2t2>15t2，－2(e－1)t>45t，得证.2.已知x1ln x1＝x2ln x2＝a，且x1<x2，求证：x2－x1<2a＋1＋e－2.证明设函数f(x)＝x ln x，f′(x)＝1＋ln x.取其在x＝e－2和x＝1处的切线，分别为l1：y＝－x－e－2和l2：y＝x－1，如图.直线y＝a与直线l1，函数f(x)的图象和直线l2分别交于x1′，x1，x2，x2′，则有：x1′<x1<x2<x2′，x2－x1<x2′－x1′＝(a＋1)－(－a－e－2)＝2a＋1＋e－2.3.设函数f(x)＝x3＋11＋x，x∈[0，1].求证：(1)f(x)≥1－x＋x2；(2)34<f(x)≤32.证明(1)因为1－x＋x2－x3＝1－（－x）41－（－x）＝1－x41＋x，由于x∈[0，1]，得1－x41＋x≤11＋x，即1－x＋x2－x3≤11＋x，从而得f(x)≥1－x＋x2.(2)由于x∈[0，1]，得x3≤x(割线放缩).故f(x)＝x3＋11＋x≤x＋11＋x－32＋32＝（x－1）（2x＋1）2（x＋1）＋32≤32.当x＝1时恰好等号能同时满足.再结合第(1)问的结论，得到f (x )≥⎝⎛⎭⎪⎫x －122＋34≥34， 又因为f ⎝ ⎛⎭⎪⎫12＝1924>34， 从而得到结论34<f (x )≤32. 二、创新拓展练4.(2021·新高考Ⅰ卷)已知函数f (x )＝x (1－ln x ).(1)讨论f (x )的单调性；(2)设a ，b 为两个不相等的正数，且b ln a －a ln b ＝a －b ，证明：2<1a ＋1b<e. (1)解 f (x )的定义域为x ∈(0，＋∞)，因为f (x )＝x (1－ln x )，则f ′(x )＝－ln x .所以当x ∈(0，1)时，f ′(x )>0，f (x )在(0，1)上单调递增；当x ∈(1，＋∞)时，f ′(x )<0，f (x )在(1，＋∞)上单调递减.综上所述，f (x )在(0，1)上单调递增，在(1，＋∞)上单调递减.(2)证明 因为b ln a －a ln b ＝a －b ，所以ln a a －ln b b ＝1b －1a， 即1＋ln a a ＝1＋ln b b， 即f ⎝ ⎛⎭⎪⎫1a ＝f ⎝ ⎛⎭⎪⎫1b . 令x 1＝1a ，x 2＝1b， 即f (x 1)＝f (x 2).由(1)可知，f (x )在(0，1)上单调递增，在(1，＋∞)上单调递减，则0<x 1<1<x 2<e.要证2<1a ＋1b<e ， 即证2<x 1＋x 2<e.①先证x 1＋x 2>2，法一(对称构造)要证x 1＋x 2>2，即证x 2>2－x 1，转化为f (2－x 1)>f (x 2)＝f (x 1)，即证f (2－x 1)－f (x 1)>0.设g (x )＝f (2－x )－f (x )，x ∈(0，1)，则g ′(x )＝ln(2－x )＋ln x ＝ln(－x 2＋2x )，当x ∈(0，1)时，g ′(x )<0，g (x )在(0，1)上单调递减，则g (x )>g (1)＝0， 所以g (x 1)＝f (2－x 1)－f (x 1)>0，即f (2－x 1)>f (x 2)＝f (x 1)，又0<x 1<1，则1<2－x 1<2，且f (x )在(1，＋∞)上单调递减，2－x 1<x 2，即x 1＋x 2>2.法二(对数均值不等式)⎩⎪⎨⎪⎧ln x >12⎝ ⎛⎭⎪⎫x －1x ，x ∈（0，1），ln x <12⎝⎛⎭⎪⎫x －1x ，x ∈（1，＋∞），⎩⎪⎨⎪⎧f （x 1）＝x 1（1－ln x 1）<x 1⎣⎢⎡⎦⎥⎤1－12⎝ ⎛⎭⎪⎫x 1－1x 1，f （x 2）＝x 2（1－ln x 2）>x 2⎣⎢⎡⎦⎥⎤1－12⎝ ⎛⎭⎪⎫x 2－1x 2， 且f (x 1)＝f (x 2)，则x 1⎣⎢⎡⎦⎥⎤1－12⎝ ⎛⎭⎪⎫x 1－1x 1>x 2⎣⎢⎡⎦⎥⎤1－12⎝ ⎛⎭⎪⎫x 2－1x 2， 即x 1＋x 2>2.②再证x 1＋x 2<e(切割线放缩).法一(割线处理)由(1)可知，f (x )的极大值点为x ＝1，极大值为f (1)＝1， 设过(0，0)，(1，1)的直线l ：y ＝x ，且f (x 1)＝f (x 2)＝m ， 当x ∈(0，1)时，f (x )＝x (1－ln x )>x ，l ：y ＝x 与y ＝m 交于点(m ，m )，则x 1<m .要证x 1＋x 2<e ，即证x 1＋x 2<m ＋x 2＝f (x 2)＋x 2<e.设h (x )＝f (x )＋x ＝x (2－ln x )，x ∈(1，e)，则h ′(x )＝1－ln x ，当x ∈(1，e)时，h ′(x )>0，h (x )在(1，e)上单调递增， 则h (x )<h (e)＝e ，所以f (x 2)＋x 2＝m ＋x 2<e ，则x 1＋x 2<m ＋x 2＝f (x 2)＋x 2<e.法二(切割线处理)设过(0，0)，(1，1)的直线l 1：y ＝x ，当x∈(0，1)时，f(x)＝x(1－ln x)>x；f(x)在(e，0)处的切线为l：y＝－x＋e，2当x∈(1，＋∞)时，f(x)＝x(1－ln x)<－x＋e，设f(x1)＝f(x2)＝m，l：y＝x与y＝m交于点(m，m)，1则x1<m，l：y＝－x＋e与y＝m交于点(－m＋e，m)，2则x2<－m＋e，所以x1＋x2<m－m＋e＝e.。

第30讲双参数最值问题知识与方法含参问题一直是高考中的重点与难点. 高考真题及模拟题中常出现“恒成立”为背景的双参数的范围或最值问题. 处理此类问题, 常用有以下方法:1消元法2零点比大小法零点比大小是指将函数y=ax+b与函数y=f(x)的零点比较大小, 进而解决问题. 图象上看, 是观察直线y=ax+b与曲线y=f(x)的横截距的大小关系. 此方法要求y=f(x)函数具有凹凸性, 可以解决形如“已知ax+b⩾f(x) (或⩽f(x))恒成立, 求b的最值”的问题,一般有如下两种形式:k(1) 若ax+b⩾f(x)恒成立, f(x)为上凸函数, 如下左图, 则x1⩽x2;(2) 若y=ax+b⩽f(x)恒成立, f(x)为下凸函数, 如下右图, 则x1⩾x2.的最值.由(1)或(2)得出x1,x2的大小,进而可以求得bk3. 赋值法对比不等式与目标式的结构, 发现当自变量取某个值时恰好构造出目标式.赋值法是零点比大小法方法的优化和改进,能快速解决线性表达式型、比值型的客观题 . 点睛意领会“等比例赋值法”进行恰到好处的赋值.典型例题【例1】若(x2+x)ln⁡1x −ax⩽23x3+(1−a)x2−2ax+b恒成立, 求b−2a的最小值 .【例2】若函数f(x)=aln⁡x+12x2+2bx在区间[1,3]上单调递增, 则a+4b的最小值为 .比值型【例3】已知函数f(x)=ln⁡x+(e−a)x−2b, 若不等式f(x)⩽0对x∈(0,+∞)恒成立, 则ba的最小值为 .【例4】已知不等式(e−a)e x+x+b+1⩽0恒成立, 其中e为自然常数, 则b+1a的最大值为 .【例5】若e x−x+12x2⩾12x2+ax+b恒成立, 求(a+1)b的最大值.【例6】已知函数f(x)=e x−xa−b, 当实数a>0时, 对于x∈R都有f(x)⩾0恒成立, 则a2b的最大值为（）A. −1e2B. 1e2C. −2e2D. 2e21.已知不等式ln⁡(x+1)−1⩽a(x+ba )对一切正数x恒成立, 则ba的最小值为 .2.已知函数f(x)=2ax2+bx−3a+1,x∈[−4,4], 若f(x)⩾0恒成立, 则5a+b的取值范围是当5a+b取得最小值时, a= .3.已知不等式x−3ln⁡x+1⩾mln⁡x+n(m≠−3)对x>0恒成立, 则n−3m+3的最大值为 .4.若对于任意正实数x, 都有ln⁡x−aex−b+1⩽0 (e 为自然对数的底数) 成立, 则a+b的最小值是 .5.已知不等式e x⩾ax+b(a,b∈R, 且a≠0)对任意实数x恒成立, 则b−2a的最大值为（）A. 2−ln⁡2B. 1−ln⁡2C. −2ln⁡2D. −ln⁡26.已知函数f(x)=e x−12x2+x3, 若x∈R时, 恒有f′(x)⩾3x2+ax+b, 则ab+ b的最大值为（）A. √eB. √e2C. e2D. e7.设函数f(x)=ln⁡(ax+b)−x(a,b∈R), 若f(x)⩽0恒成立, 则ab的最大值为 .8.已知a≠0, 函数y=f(x)=ae x,y=g(x)=ealn⁡x+b ( e为自然对数的底数), 若存在一条直线与曲线y=f(x)和y=g(x)均相切, 则ba最大值是 .切线放缩知识与方法1. 切线放缩对于含有指数、对数或三角函数等超越式的函数或不等式问题, 有时我们可以利用导数的几何意义进行以直代曲, 即考虑函数f(x)图象上某点x=x0处的切线y=kx+b, 结合函数的凹凸性进行切线放缩, 使问题便于解决.特别地, 当f(x)⩾kx+b为下凸函数时, 则f(x)⩾kx+b; 当f(x)为上凸函数时, 则f(x)⩽kx+b. 两个不等式中等号成立的条件刚好是x=x0.将f(x)放大或缩小为kx+b, 得到f(x)⩾kx+b或f(x)⩽kx+b, (其中k=f′(x0),y=kx+b为f(x)在x=x0处的切线y=f′(x0)(x−x0)+f(x0))叫做切线放缩.对某些求函数的最小值或证明不等式的问题, 巧用切线放缩, 会有意想不到的效果.2. 常用的切线不等式x;(5)sin⁡x⩽x(x⩾0).(1) e x⩾x+1;(2)ln⁡x⩽x−1;(3)e x⩾ex;(4)ln⁡x⩽1e【点睛】在e x⩾x+1中, 将x换成ln⁡x, 即得x⩾ln⁡x+1⇒ln⁡x⩽x−1;在e x⩾x+1中, 将x换成x−1, 即得e x−1⩾x⇒e x⩾ex;x;在e x⩾ex中, 将x换成ln⁡x, 即得x⩾elnx⇔ln⁡x⩽1e在ln⁡x⩽x−1中, 将x换成x+1, 即得ln⁡(x+1)⩽x.典型例题逆用求导法则型【例1】若x,y是实数, e是自然对数的底数, e x+y+2−3⩽ln⁡(y−2x+1)+3x, 则2x+y= .【例2】已知函数f(x)=ax+ln⁡x+1, 若对任意的x>0,f(x)⩽xe2x恒成立, 则求实数a的取值范围是 .【例3】已知a1,a2,a3,a4成等比数列, 且a1+a2+a3+a4=ln⁡(a1+a2+a3), 若a1>1, 则（）A. a1<a3,a2<a4B. a1>a3,a2<a4C. a1<a3,a2>a4D. a1>a3,a2>a4多变量轮换式的切线放缩【例4】f(x)=3+x1+x2,x∈[0,3], 已知数列{a n}满足0<a n⩽3,n∈N∗, 且满足a1+ a2+⋯+a2010=670, 则f(a1)+f(a2)+⋯+f(a2010)=A. 有最大值 6030B. 有最大值 6027C. 有最小值 6027D. 有最小值 6030双参数最值的切线放缩【例5】已知不等式ln⁡(x+1)−1⩽a(x+ba )对一切正数x恒成立, 则ba的最小值为 .强化训练1.已知函数f(x)=e x−1,g(x)=ln⁡(x+1), 直线l与y=f(x)的图象相切, 与y= g(x)的图象也相切, 则直线的l方程是 .2.已知实数a,b,c满足e a+c+e2b−c−1⩽a+2b+1 (e 为自然对数的底数), 则a2+b2的最小值是 .3.函数f(x)=e x−a+x,g(x)=ln⁡(x+2)−4e a−x, 若∃x0使得f(x0)−g(x0)=3, 则a= .。

高中数学导数切线放缩法
《高中数学导数切线放缩法》
一、定义
导数切线放缩法是一种将数学函数的导数按一定的比例缩放后，然后在y方向上放缩的一种常用方法。

二、原理
利用放缩法，可以把目标函数的导数放大，使得曲线的斜率变大，从而达到快速收敛的效果。

放缩前，函数的导数变换前后的变化比较慢，放缩后，函数的导数变换前后的变化较快，从而实现快速收敛。

三、应用
1.高中数学作业中，利用导数切线放缩法可以快速的求出函数的单调性、极值点以及图像的放大和缩小等。

2.在机器学习中，利用导数切线放缩法可以实现快速的权重调整，从而提升算法的学习速率。

- 1 -。

高中数学知识点总结导数的应用之函数的单调性与曲线的凹凸性之函数的凹凸区间函数的单调性与曲线的凹凸性是高中数学中导数应用的重要内容之一。

通过研究函数的单调性和凹凸性，可以帮助我们更好地理解函数的性质和图像的形态。

本文将从函数的凹凸定义及性质出发，介绍函数的凹凸区间的求解方法，并结合实例进行分析。

一、函数的凹凸定义及性质函数的凹凸性是指函数图像在一段区间上的形态特征，可以帮助我们判断函数的增减趋势和曲线的弯曲情况。

1. 凹函数与凸函数的定义：设函数f(x)在区间I上可导，若对于任意x1、x2∈I，且x1<x2，在I上有：f(x2)-f(x1)≥f'(x)(x2-x1)，则称函数f(x)在I上为凹函数；若对于任意x1、x2∈I，且x1<x2，在I上有：f(x2)-f(x1)≤f'(x)(x2-x1)，则称函数f(x)在I上为凸函数。

2. 凹函数与凸函数的性质：（1）若函数f(x)在区间I上连续，则凹函数在I上内任意两点之间的所有点都在对应的切线下方，凸函数在I上内任意两点之间的所有点都在对应的切线上方。

（2）若函数f(x)在区间I上有二阶导数，且f''(x)>0，则f(x)在I上为凹函数；若f''(x)<0，则f(x)在I上为凸函数。

（3）若函数f(x)在区间I上为凹函数，则f'(x)在I上单调递增；若函数f(x)在区间I上为凸函数，则f'(x)在I上单调递减。

二、函数的凹凸区间求解方法对于给定的函数f(x)，我们可以通过以下步骤求解其凹凸区间：步骤一：求函数f(x)的一阶导数f'(x)和二阶导数f''(x)；步骤二：求解f''(x)=0的解，得到临界点；步骤三：将临界点和定义域的端点带入二阶导数f''(x)的值，确定函数f(x)的凹凸性；步骤四：根据凹凸性的变化，确定函数f(x)的凹凸区间。

题 型：切线放缩问题解法突破：顾名思义是构造函数不等式的一种常用方法，多用于将指数、对数、无理根式统一到一阶幂函数的形式，用时还需考虑函数的凹凸性（凹凸性过于复杂的函数需慎用），难点是寻找切线放缩的位置？通常于端点处进行放缩，不行的话后移选取特殊点，若还是搞不定则需要待定系数法进行选取。

此法虽误差较大，但效果明显，出师亦多建奇功！例 题：（改编题）求证：2ln x e x x >+（0x >）分析与解：函数左凹右凸，适合切线放缩，但从何处放缩呢？此时不妨用筛法，在你的知识体系中不断搜寻，一一试验，例如：1，1x e x ≥+，x e ex ≥，224x e x e ≥，212x x e x ≥++（为常用不等式，法2）2，1ln x x -≥，2ln ex x -≥，ln x x e≥，…… 但不等式繁多，从来源处一一搜寻则工程浩大，题干中亦未给出更多的提示条件，故不可取，不妨用待定系数为取值创造一些条件。

选取切点()11,x x e 与()222,2ln x x x +，分别构造切线，有 ()11122112ln 12ln x x x e e x x e x x x x x ⎛⎫≥+->++-≥+ ⎪⎝⎭ 即1212x e x =+，()1121ln 1x x e x ->-，不妨取11x =，212x e =-.上述为分析过程，不可以此为解题步骤，需诸君按此编写答案即可，不赘述。

变式训练：（2018·湖北模拟改）若0x >，求证：2181224xx e x x x -⋅>++++.归纳总结：变式训练需进行224xe x e ≥12x ≥+两处放缩，都不大容易想，希望各位同学，慢慢参悟。

____________________________________________________________ ___________________________________________________________________________________________________________________________________.以下为本人精选或改编的一些练习，陈列于此仅供参考！1，136ln x x e -<；2，()11ln 2x x e x -->-； 3，（2006·港澳竞赛）（此为切线放缩的一个妙用）已知,,,a b c d 是满足1a b c d +++=的正数，求证：()()33332222168a b c d a b c d +++≥++++. 4，若0i x >，（1,2,3i =），且311i i x ==∑，则2221231112711110A x x x =++≤+++.（其他条件不变，若313i i x ==∑，试证明32A ≥.） 5，,,a b c 为实数，证明32a b c b c a c a b ++≥+++. 6，已知,a b 为正实数，且2a b +=，求证：1111ln ln 2a a b b +++≥. 7，若,y,z x 为非负实数，且222y z 1x ++=，证明：222331114x y z x y z ++≤+++.。

导数专题之切割线放缩切线放缩若函数()y f x =在区间[,]a b 上有凹凸性，可以利用切线()()()000'y f x x x f x =-+进行放缩． （1）若函数()y f x =的图象在区间[,]a b 下凸（''()0f x >），则有：()()()000()'f x f x x x f x ≥-+； （2）若函数()y f x =的图象在区间[,]a b 上凸（''()0f x <），则有：()()()000()'f x f x x x f x ≥-+.割线放缩若函数()y f x =在区间[,]a b 上有凹凸性，可以利用割线()()()()f b f a y x a f a b a-=-+-进行放缩．（1）若函数()y f x =的图象在区间[,]a b 下凸（''()0f x >），则有：()()()()()f b f a f x x a f a b a -≤-+-；（2）若函数()y f x =的图象在区间[,]a b 上凸（''()0f x <），则有：()()()()()f b f a f x x a f a b a-≥-+-.附 函数凹凸性的定义1、凹函数定义：设函数()y f x =在区间I 上连续，对12,x x I ∀∈，若恒有1212()()()22x x f x f x f ++<，则 称()y f x =的图象是上凹/下凸的，函数()y f x =为上凹/下凸函数；二阶导数''()0f x > 2、凸函数定义：设函数()y f x =在区间I 上连续，对12,x x I ∀∈，若恒有1212()()()22x x f x f x f ++>，则 称()y f x =的图象是下凹/上凸的，函数()y f x =为下凹/上凸函数. 二阶导数''()0f x <1.已知(0,)x e∈，求证：()22222lnln2ln25e e x x ex x-+>++2.求证：1 (1)ln2xx e x-->-练习：(1)ln1xe e x x x≥-++；12ln1xxee xx-+>；233125ln02x xx x x-++-->3.已知,,0a b c>且1a b c++=，求证：4.4.已知,0a b>且1a b+=，求证：3≥.5.已知23()1xf x x +=+，[0,3]x ∈，已知数列{}n a 满足03n a <≤，*n N ∈，且122010670a a a +++=L ，则()()()122010f a f a f a +++L 的最大值为______．(6030)构造[0,3]x ∈上的函数不等式：239131103x x x +⎛⎫≤-⋅-+ ⎪+⎝⎭.6.求函数y =的值域．7.已知,0a b >且1a b +=，求.8.已知,0a b ≥，1a b +=，则______，最小值是_______．9.已知,,a b c 满足1a b c ++=的最值.10.已知1122ln ln x x x x a==，12x x <，求证：22121x x a e --<++.11.设,,a b c 为非负实数，满足1a b c ++=，则222111222ab c +++++的取值范围是______．12.已知0,2x π⎛⎫∈ ⎪⎝⎭，求证：cos tan 2x x x +>．13.已知,0a b >，4a =，则31a b +的最小值是_______．14.已知1nii xn==∑，求()12inx ii x =⋅∑的最小值．例1、()[]23,0,31xf x x x +=∈+，已知数列{}n a 满足03,n a n N *<≤∈，且满足122010670a a a +++=L ，则122010()()()f a f a f a +++L = 6030例2、已知函数2901xf x a ax =>+()() ．（1）求f x ()在122[,]上的最大值；（2）若直线2y x a =-+为曲线y f x =()的切线，求实数a 的值；（3）当2a =时，设1214122x x x ,⎡⎤∈⎢⎥⎣⎦…,,, ，且121414x x x =…+++ ，若不等式1214f x f x +f x λ≤…()+()+()恒成立，求实数λ的最小值．例3、若)3,2,1(,0=>i x i ，且311i i x ==∑，则2111x ++2211x ++2311x +≤2710例4、若实数,,0a b c >，证明：23≥+++++b a c c a b c b a .练习1：已知函数)2()20()2(11)(2>≤≤⎪⎩⎪⎨⎧++=x x f x x x f ，⑴求函数)(x f 在定义域上的单调区间.⑵若关于x 的方程0)(=-a x f 恰有两个不等的实根，求实数a 的范围；⑶已知实数]1,0[,21∈x x ，121=+x x ，若不等式)ln()()(21p x x x f x f --≤在),(+∞∈p x 上恒成立，求实数p 的最小值.（可以利用切线求)()(21x f x f 的最大值）练习2：若z y x ,,非负，且1222=++z y x ，证明：43111222≤+++++z z y y x x 提示：平衡点是33=x .21)(x xx f +=在33=x 的切线12321+=x y ，有12321)(+≤x x f15.已知函数1()x e f x x -=（1）求函数()f x 的单调区间；（2）若2ln 10xe x x kx ---≥对任意实数0x >都成立，求k 的取值范围.答 案1.已知(0,)x e ∈，求证：()22222ln ln 2ln 25e e x x e x x -+>++ 解：原式等价于()()2ln 121(ln 1)ln 2ln 25x e e x x x --->++令ln 1 (0)t x t =-<，即证：()2214155te et t t ->++ 取e e t y t =-在0t =处的切线，有(1)1,0te et e t t ->-+<()2222[(1)1](1)2(1)1te et e t e t e t ->-+=---+当0t <时，有22214(1),2(1)55e t t e t t->-->，得证.2.求证：1(1)ln 2x x e x -->-解：① 当1x ≥时用切线放缩 1xe x ≥+1(1)(1)ln (1)(1)(1)(1)2LHS x x x x x x x x ≥-+->-+--=->-② 当01x <<时用割线放缩(1)1x e e x <-+ [][]11(1)(1)1ln (1)(1)1(1)(1)(1)42e LHS x e x x x e x x e x x -≥--+->--+--=--≥->-练习：(1)ln 1xe e x x x ≥-++；12ln 1x xe e x x -+>；233125ln 02x x x x x -++-->3.已知,,0a b c >且1a b c ++=，求证：222233131314.a b c +++++<…解一：利用勾股定理刻画不等式中的几何意义．解二：利用切线和割线构造了函数不等式：2233131 1.323x x x ⎛⎫+-≤+≤+ ⎪⎝⎭加和即得证.4.已知,0a b>且1a b+=，求证：3≥.法一均值不等式=≥≥3≥≥=法二切线法2x≥-，当12x=时取等.()2243a b a b≥-+-=-+=，取等条件：12a b==.5.已知23()1xf xx+=+，[0,3]x∈，已知数列{}n a满足03na<≤，*n N∈，且122010670a a a+++=L，则()()()122010f a f a f a+++L的最大值为______．(6030)构造[0,3]x∈上的函数不等式：239131103xxx+⎛⎫≤-⋅-+⎪+⎝⎭.6.求函数y=的值域．解：定义域：[] 3,5为上凸函数，于是3x≥-)5x≥-)3513222y x x x⎛=---=-+-≥⎝⎭当且仅当3x=时取等.()()2357210x x x x≤-+--+-=当且仅当7235x xx x--=--，即297x=时取等.于是函数值域为.7.已知,0a b>且1ab+=，求.解：设函数()f x=()g x='()f x=，'()g x=取这两个函数平行的切线，有=2240119b a-=与1a b+=联立，解得12,33ab==1233a b⎫⎫--+=⎪⎪⎭⎭8.已知,0a b≥，1a b+=，则______，最小值是_______．法一割线放缩处理最大值.1)1a≤+(7b≤等号当,{0,1}ab∈时取得．于是有1)32(7a b≤+++考虑到1)2(7>-，于是当()(),1,0a b =时右边取得最大值．因此所求的最大值为切线放缩处理最小值．)a λ≥-，)b μ≥-等号当(,)(,)a b λμ=时取得．令112,3233λμλμ+=⎧⎪⇒==⎨=⎪⎩≥= 等号当12(,),33a b ⎛⎫= ⎪⎝⎭时取得．因此所求的最小值为 法二令()01f x x ==≤≤9.已知,,a b c 满足1a b c ++=的最值.解：设函数()f x =14x ≥-，'()f x =作出函数()f x 的图象，函数()f x 的图象在13x =处的切线：1733y x ⎛⎫=-+ ⎪⎝⎭，以及函数()f x 的图象过点1,04⎛⎫- ⎪⎝⎭和1,04⎛⎫- ⎪⎝⎭的割线：y x =+，如图．1733x x ⎫≤-+⎪⎝⎭左侧等号当14x =-或32x =时取得；右侧等号当13x =，当13a b c ===，当14a b ==-，32c =时取得．10.已知1122ln ln x x x x a==，12x x <，求证：22121x x a e --<++.解：设函数()ln f x x x =，()1ln .f x x '=+取其2x e -=在和1x =处的切线，分别为21:el y x -=--和2:1l y x =-，如图．直线y a =与直线1l ，函数()f x 的图象和直线2l分别交于1122',,,'x x x x ，则有：1122''x x x x <<<()222121(1)21x x x x a a e a e ''---<-=+---=++注1 类似的，我们还可以用割线y x =-和1(1)1y x e =--来估计21x x -的下界，如图．注2 我们也可以利用函数图象的外接曲线得到更加精确的界，例如用21(1)12y x x =-+-和2y e =-如图．11.设,,a b c 为非负实数，满足1a b c ++=，则222111222ab c +++++的取值范围是______． 设函数21()2f x x =+，考虑利用切割线放缩得到辅助不等式：当[0,1]x ∈时，有：21115419622361319x x x ⎛⎫-+≤≤--+ ⎪+⎝⎭ 且左边不等式等号当0,1x =时取得；右边不等式等号当13x =时取得．左边不等式为：(1)(2)0x x x --≥，右边不等式为：2(176)(31)0x x --≥，容易得证. 所以()135427()16236119x f x x -+≤≤--+∑∑∑222411127322219a b c ≤++≤+++左侧等号当()(),,1,0,0x y z =时可以取得；右侧等号当111(,,),,333x y z ⎛⎫= ⎪⎝⎭时可以取得．因此所求的取值范围是427,319⎡⎤⎢⎥⎣⎦．12.已知0,2x π⎛⎫∈ ⎪⎝⎭，求证：cos tan 2x x x +>． 解：先证 0,,sin tan 22x x x xπ⎛⎫∀∈+> ⎪⎝⎭于是当0,4x π⎛⎤∈ ⎥⎝⎦时，有 cos tan sin tan 2x x x x x +≥+> 当,42x ππ⎛⎫∈ ⎪⎝⎭时，利用cos y x =在4x π=和2x π=之间的割线，有cos 2x x ππ⎫>--⎪⎝⎭利用tan y x =在4x π=处的展开，有 2tan 12244x x x ππ⎛⎫⎛⎫>+-+- ⎪ ⎪⎝⎭⎝⎭ 于是当,42x ππ⎛⎫∈ ⎪⎝⎭时，有22cos tan 21228x x x x x πππ⎫+->+-++⎪⎪⎝⎭右侧对应的28480ππ∆=+-<，得证.13.已知,0a b >，4a =，则31a b +的最小值是_______． 根据切割线放缩，有14(1)33a a b =≥+-+，于是433b a +≤进而3143a b a +≥≥+等号当且仅当()(),1,1a b =时取得．因此所求的最小值为4．14.已知1nii xn==∑，求()12inx ii x =⋅∑的最小值．解 切线放缩,2(ln 42)(1)2xx R x x ∀∈⋅≥+-+ ()()112(ln 42)122innx i ii i x x n n==⋅≥++∴-=∑∑当1i x =时取到等号，从而得到所求的最小值为2n ．注 切比雪夫不等式亦可解.例1、()[]23,0,31xf x x x +=∈+，已知数列{}n a 满足03,n a n N *<≤∈，且满足122010670a a a +++=L ，则122010()()()f a f a f a +++L = 6030解析：3)31(f =因为，当12201013a a a ====L 时，122010()()()f a f a f a +++L =6030 对于函数23()(03)1x f x x x +=≤≤+,19()316k f '==-,在13x =处的切线方程为即3(11)10y x =-，则()22331(11)(3)()01103x f x x x x x +=≤-⇔--≤+成立，所以当03,n a n N*<≤∈时，有()3(113)10n n f a a ≤-122010()()()f a f a f a +++L []12201031120103()603010a a a ≤⨯-+++=L例2、已知函数2901xf x a ax =>+()() ．（1）求f x ()在122[,]上的最大值；（2）若直线2y x a =-+为曲线y f x =()的切线，求实数a 的值；（3）当2a =时，设1214122x x x ,⎡⎤∈⎢⎥⎣⎦…,,, ，且121414x x x =…+++ ，若不等式1214f x f x +f x λ≤…()+()+()恒成立，求实数λ的最小值．解析：（1）2222229[1(1)2]9(1)()(1)(1)ax x ax ax f x ax ax ⋅+-⋅-'==++， 令，解得（负值舍去），由，解得．（ⅰ）当时，由1[,2]2x ∈，得()0f x '≥，∴在上的最大值为18(2)41f a =+． （ⅱ）当时，由1[,2]2x ∈，得()0f x '≤，∴在上的最大值为118()24f a =+． （ⅲ）当时，在时，，在时，， 在上的最大值为． （2）设切点为，则()1,()2.f t f t t a '=-⎧⎨=-+⎩由，有，化简得， 即或， …① 由()2f t t a =-+，有，…②()0f x '=x =122<<144a <<104a <≤()f x 1[,2]24a ≥()f x 1[,2]2144a <<Q 12x a <<()0f x '>2x a <<()0f x '<∴()f x 1[,2]2f (,())t f t ()1f t '=-2229[1]1(1)at at -=-+2427100a t at -+=22at =25at =2921ta tat =-+由①、②解得或． （3）当时，，由（2）的结论直线为曲线的切线，，点在直线上，根据图像分析，曲线()y f x =在线下方．下面给出证明：当时，． ，当时，()(4)0f x x --≤，即． ∴，，．要使不等式恒成立，必须．又当时，满足条件，且，因此，的最小值为．例3、若)3,2,1(,0=>i x i ，且311i i x ==∑，则2111x ++2211x ++2311x +≤2710证明：设21()1g x x =+，则()222'()1xg x x -=+ ，()()232231''()1x g x x -=+， 由''()0g x <得x <<，''()0g x >得x >或x <，故21()1g x x =+在33⎡-⎢⎣⎦是上凸的，在区间,3⎛-∞- ⎝⎭，3⎛⎫+∞ ⎪ ⎪⎝⎭是下凸的. 2a=a =2a =29()12xf x x =+4y x =-()y f x =(2)2f =Q ∴(2,(2))f 4y x =-4y x =-1[,2]2x ∈()4f x x ≤-3222928104()(4)41212x x x x f x x x x x -+---=-+=++Q 2221(2)12x x x --=+（）1[,2]2x ∈()4f x x ≤-12141214()()()414()f x f x f x x x x +++≤⨯-+++L L 121414x x x +++=Q L 1214()()()561442f x f x f x ∴+++≤-=L ∴1214()()()f x f x f x λ+++≤L 42λ≥Q 12141x x x ====L 121414x x x +++=L 1214()()()42f x f x f x +++=L λ42由311ii x==∑，则平衡值013x =，由导数知识易求得()g x 在13x =处的切线为27(2)50y x =- ，因013x ⎡=∈⎢⎣⎦，()g x在⎡⎢⎣⎦是上凸的，故()2127()2150g x x x =≤-+恒成立.即()1211272150x x ≤-+，()2221272150x x ≤-+，()3231272150x x ≤-+，三式相加并结合311ii x ==∑即得2111x ++2211x ++2311x +≤2710.若将该题条件改为：若)3,2,1(,0=>i x i ，且313ii x==∑时，解法同理.此时平衡值01x =，而21()1g x x =+在1x =处的切线为112y x =-+,因01x ⎫=∈+∞⎪⎪⎝⎭，()g x在⎫+∞⎪⎪⎝⎭是下凸的，故211()112g x x x =≥-++恒成立.即12111112x x ≥-++，22211112x x ≥-++，32311112x x ≥-++，三式相加并结合313ii x ==∑即得2111x ++2211x ++2311x +≥32.即得一个新的不等式：若1,2,33i x i >=，且313ii x ==∑，则2111x ++2211x ++2311x +≥32.所以，在证明一类多元不等式时，我们经常用到的一个办法就是假设这些变元的和为1.例4、若实数,,0a b c >，证明：23≥+++++b a c c a b c b a .提示：不妨设0a b c t ++=>，则平衡点是3t x =.x x x f -=1)(在3t x =处的切线()2293x t y t -=-，有()229()3x t f x t -≥-.5、若z y x ,,非负，且1222=++z y x ，证明：43111222≤+++++z z y y x x 提示：平衡点是33=x .21)(x xx f +=在33=x 的切线12321+=x y ，有12321)(+≤x x f练习1：已知函数)2()20()2(11)(2>≤≤⎪⎩⎪⎨⎧++=x x f x x x f ，⑴求函数)(x f 在定义域上的单调区间.⑵若关于x 的方程0)(=-a x f 恰有两个不等的实根，求实数a 的范围；⑶已知实数]1,0[,21∈x x ，121=+x x ，若不等式)ln()()(21p x x x f x f --≤在),(+∞∈p x 上恒成立，求实数p 的最小值.（可以利用切线求)()(21x f x f 的最大值）练习2：若z y x ,,非负，且1222=++z y x ，证明：43111222≤+++++z z y y x x 提示：平衡点是33=x .21)(x xx f +=在33=x 的切线12321+=x y ，有12321)(+≤x x f 切线放缩法实质就是利用函数的图像性质解决一类多元的问题向一元函数求最值和类型的不等式转化.此时，可以选择先求二阶导看凹凸性，判断这个函数是否能使用切线法，或者能够被用得比较好.也可以直接选择求一阶导，把等号取道条件的切线值求出来，对应不等式常数项配最后的常数系数.其本质相当于求这个一元函数在等号取到条件时（也就是文中的平衡点）的切线值，进一步求对于这个一元函数相对应的某个局部不等式.15.已知函数1()x e f x x -=（1）求函数()f x 的单调区间；（2）若2ln 10xe x x kx ---≥对任意实数0x >都成立，求k 的取值范围.解：（1）2(1)1'()x e x f x x -+=设()(1)1x x e x ϕ=-+，'()xx e x ϕ=⋅ 于是()x ϕ在(),0-∞上单调递减，在()0,+∞上单调递增，在0x =处取得极小值，亦为最小值(0)0ϕ=，因此()f x 在R 单调递增．（2）12ln 102ln x xe e x x kx k xx ----≥⇒≤-设 1()2ln x e x x x μ-=-，21(1)2'()x e x xx x μ+--=其极值点在1x =附近．因此考虑在1x =处进行切线放缩，有 12x e x e x -≥+-()22ln x x e x μ≥+-- 设()2ln 2h x x x e =-+-，2'()1h x x =-在2x =取最小值，(2)2ln 2h e =-，即2ln 2k e ≤-.。