第三章力矩平面力偶系a

第三章 力对点的矩和平面力偶系一、内容提要本章研究了力矩和力偶。

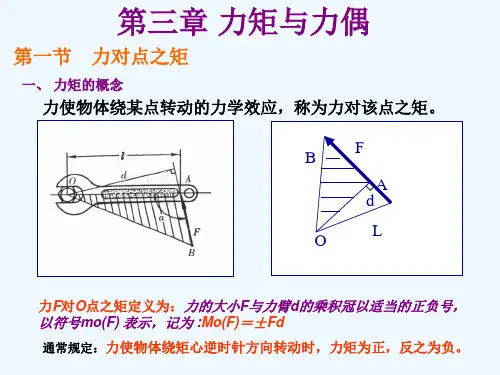
1．力矩及计算（1）力矩 力矩表示力使物体绕矩心的转动效应。

力矩等于力的大小与力臂的乘积。

在平面问题中它是一个代数量。

一般规定：力使物体绕矩心产生逆时针方向转动为正，反之为负。

用公式表达为()Fd F M O ±=（2）合力矩定理 平面汇交力系的合力对平面内任一点的力矩，等于力系中各力对同一点的力矩的代数和。

用公式表达为()()F M F M O O ∑=R2．力偶的基本理论（1）力偶 由两个大小相等、方向相反、不共线的平行力组成的力系，称为力偶。

力偶与力是组成力系的两个基本元素。

（2）力偶矩 力与力偶臂的乘积称为力偶矩。

为代数量，规定：逆时针方向转动为正，反之为负。

用公式表达为：Fd M ±=（3）力偶的性质力偶不能合成为一个合力，不能用一个力代替，力偶只能与力偶平衡。

力偶在任一轴上的投影恒为零。

力偶对其平面内任一点矩都等于力偶矩，与矩心位置无关。

在同一平面内的两个力偶，如果它们的力偶矩大小相等，转向相同，则这两个力偶等效。

力偶对物体的转动效应完全取决于力偶的三要素：力偶矩的大小、力偶的转向和力偶所在的作用面。

（4）平面力偶系的合成与平衡平面力偶系的合成结果为一个合力偶，合力偶矩等于平面力偶系中各个力偶矩的代数和。

用公式表达为：M R =ΣM平面力偶系的平衡条件是合力偶矩等于零。

用公式表达为：ΣM = 0二、思考题提示或解答3-1 试比较力矩与力偶矩的异同点。

答：平面汇交力系的合力对平面内任一点的力矩，等于力系中各分力对同一点的力矩的代数和。

这就是平面力系的合力矩定理。

应用合力矩定理在于简化力矩的计算。

当力臂不易确定时，可将力分解为易找到力臂的两个互相垂直的分力，在求出两分力的力矩后，再代数相加即可。

3-3 二力平衡中的两个力，作用与反作用公理中的两个力，构成力偶的两个力各有什么不同?答：二力平衡中的两个力等值、反向、共线，共同作用在一个物体上；作用与反作用公理中的两个力等值、反向、共线，分别作用在两个物体上； 构成力偶的两个力等值、反向、互相平行，也作用在一个物体上。

理论⼒学第三章⼒矩与平⾯⼒偶理论（H）第3章⼒矩与平⾯⼒偶理论※平⾯⼒对点之矩的概念及计算※⼒偶及其性质※平⾯⼒偶系的合成与平衡※结论与讨论§3-1 平⾯⼒对点之矩的概念及计算1.⼒对点之矩AFBhhF M O ?±=)(F h ——⼒臂O ——矩⼼OABM O Δ±=2)(F M O (F ) ——代数量（标量）“＋”——使物体逆时针转时⼒矩为正；“－”——使物体顺时针转时⼒矩为负。

2. 合⼒之矩定理平⾯汇交⼒系合⼒对于平⾯内⼀点之矩等于所有各分⼒对于该点之矩的代数和。

3. ⼒矩与合⼒矩的解析表达式xA FF xF yOαyx yx y y O x O O yF xF M M M ?=+=)()()(F F F )()()()()(21i O n O O O R O M M M M M F F F F F ∑=+++=")()(ix i iy i R O F y F x M ?∑=FF nαOrF rF 已知：F n ，α，r求：⼒F n 块对轮⼼O 的⼒矩。

h解：（1）直接计算αcos )(r F h F M n n n O ==F （2）利⽤合⼒之矩定理计算αcos )()()()(r F M M M M n O O r O n O ==+=F F F F 例题1§3-2 ⼒偶及其性质1.⼒偶与⼒偶矩⼒偶——两个⼤⼩相等、⽅向相反且不共线的平⾏⼒组成的⼒系。

⼒偶臂——⼒偶的两⼒之间的垂直⼒偶的作⽤⾯——⼒偶所在的平⾯。

（1）⼒偶不能合成为⼀个⼒，也不能⽤⼀个⼒来平衡。

⼒和⼒偶是静⼒学的两个基本要素。

（2）⼒偶矩是度量⼒偶对刚体的转动效果；它有两个要素：⼒偶矩的⼤⼩和⼒偶矩的转向。

F′FABOdx FdFxxdFMMMOOO=+′=′+=′)()()(),(FFFF⼒偶矩±=FdM2.平⾯⼒偶的等效定理1F ′F ′2F ′0F ′F 00F ′F 0ABDCdF F 1F 2★在同平⾯内的两个⼒偶，如果⼒偶矩相等，则两⼒偶彼此等效。

第三章力对点之矩与平面力偶一、判断题1、力偶是物体间相互的机械作用，这种作用的效果是使物体的运动状态发生改变。

力偶没合力，不能用一个力来等效代换，也不能用一个力来与之平衡。

（√）2、力偶使物体转动的效果完全由力偶矩来确定，而与矩心位置无关。

只要力偶矩相同，不管其在作用面内任意位置，其对刚体的作用效果都相同。

（√）3、01=∑=n i i M是平面力偶系平衡的充要条件。

（√）4、半径为R 的圆轮可绕通过轮心轴O 转动，轮上作用一个力偶矩为M 的力偶和一与轮缘相切的力F,使轮处于平衡状态。

这说明力偶可用一力与之平衡。

（×）5.刚体的某平面内作用一力和一力偶，由于力与力偶不能等效，所以不能将它们等效变换为一个力。

（×）解析：一个力和一个力偶可以简化为一个力。

6、物体受同一平面内四个力的作用，这四个力组成两个力偶（F1，F1′）和(F2,F2′），其组成的力多边形自行封闭，该物体处于平衡。

（×）7、力偶不是基本力学量，因为构成力偶的两力为基本量。

（×）解析：(1)力学中的基本物理量是长度、质量、时间。

(2)国际单位制中的基本单位：长度，米（m）；质量，千克（kg）；时间，秒（s）；电流，安（A）；热力学温度，开（K）；物质的量，摩（mol)；发光强度，坎（cd）。

8、自由刚体受到力偶作用时总绕力偶臂中点转动。

（×）解析：动力学可以证明，静止的自由刚体受力偶作用时，总是绕着刚体的质量中心转动（与质量分布有关，与作用位置无关）。

9、力偶的合力等于零。

（×）解析：力偶是一对大小相等方向相反但不在同一条直线上的两个力,这与力的平衡定理作用在同一直线上的两个力大小相等方向相反则两力平衡是相悖的.力偶对平面内任意点的力矩不为零.10、力偶的合成符合矢量加法法则。

（×）解析：三角形法则，平行四边形法则。

三角形法则是：如果是两个矢量的相加将这两个矢量的首尾相接，从一个矢量的开头指向另一个矢量的末尾就是它们的和向量。