对流扩散方程的数值计算
- 格式:pdf
- 大小:177.23 KB
- 文档页数:5


对流扩散反应方程的cfl条件对流扩散反应方程是描述物质传输过程中同时考虑了对流、扩散和反应的数学模型。
在数值计算中,为了确保计算结果的准确性和稳定性,需要满足CFL( Courant-Friedrichs-Lewy)条件,该条件是一种数值稳定性条件,能够控制时间步长的选取。
CFL条件的提出CFL条件是由Richard Courant、Kurt Friedrichs和Hans Lewy在1928年提出的。
他们发现,在求解偏微分方程的数值计算中,存在一个与物理问题无关的数值稳定性条件,即CFL条件。
当时间步长超过CFL条件时,数值解就会出现不稳定、震荡以及计算结果不准确等问题。
CFL条件的定义CFL条件是根据对流速度、网格尺寸和扩散系数之间的关系来定义的。
在对流扩散反应方程中,对流项的影响取决于对流速度,而扩散项的影响取决于网格尺寸和扩散系数。
CFL条件的定义如下:CFL条件 = 对流速度 ×时间步长 / 网格尺寸≤ 1其中,对流速度是描述物质在流动中传输的速度,时间步长是数值计算中的时间间隔,网格尺寸是用来离散化空间的单元大小。
CFL条件的意义CFL条件的意义在于保证数值计算的稳定性。
当满足CFL条件时,数值解才能保持稳定,不会发散或者出现震荡现象。
否则,如果时间步长选取过大或网格尺寸选取过小,会导致计算结果不准确,甚至影响到计算的收敛性。
满足CFL条件的选择为了满足CFL条件,需要合理选择时间步长和网格尺寸。
一般来说,时间步长与网格尺寸的比值需要小于或等于对流速度,即:时间步长 / 网格尺寸≤ 对流速度 / 扩散系数这样可以确保数值计算的稳定性和准确性。
当网格尺寸变小时,要相应减小时间步长,以保持CFL条件的满足。
总结对流扩散反应方程的CFL条件是一种数值稳定性条件,可以有效控制数值计算的稳定性和准确性。
合理选择时间步长和网格尺寸,以满足CFL条件,是进行对流扩散反应方程数值计算的重要一步。


一维对流扩散方程是指一维均匀的边界层上的传质过程的数学模型,常用于描述对流扩散过程中的温度、湿度、速度等场的分布情况。
一维对流扩散方程的数学形式为:∂φ/∂t+U∂φ/∂x=D∂^2φ/∂x^2其中φ表示传质物质的浓度,t表示时间,x表示空间坐标,U表示对流速度,D表示扩散系数。
二维对流扩散方程是指二维均匀的边界层上的传质过程的数学模型,常用于描述对流扩散过程中的温度、湿度、速度等场的分布情况。
二维对流扩散方程的数学形式为:∂φ/∂t+U∂φ/∂x+V∂φ/∂y=D∂^2φ/∂x^2+D∂^2φ/∂y^2其中φ表示传质物质的浓度,t表示时间,x和y分别表示两个空间坐标,U和V分别表示两个方向上的对流速度,D表示扩散系数。
单调差分格式是一种常用的数值求解方法,它通过进行差分运算来求解微分方程的数值解。
在求解一维和二维对流扩散方程时,可以使用单调差分格式来解决。
具体来说,可以将空间坐标和时间分别离散化,将对流扩散方程转化为一个线性方程组,然后使用单调差分格式来解决。
单调差分格式的具体形式取决于方程的类型和离散化的方式,但一般来说,它都是将微分方程的差分形式写成一个线性方程组的形式。
例如,在求解一维对流扩散方程时,可以使用下面的单调差分格式:φ_i^{n+1}=φ_i^n+Δt(D(φ_{i+1}^n-2φ_i^n+φ_{i-1}^n)/Δx^2+U(φ_ {i+1}^n-φ_{i-1}^n)/2Δx)其中φ_i^n表示第i个网格点在时间步n的浓度值,Δx和Δt分别表示网格的空间步长和时间步长。
同样的,在求解二维对流扩散方程时,可以使用下面的单调差分格式:φ_i^n=φ_i^n+Δt(D(φ_{i+1,j}^n+φ_{i-1,j}^n+φ_{i,j+1}^n+φ_{i,j-1}^ n-4φ_i^n)/Δx^2+U(φ_{i+1,j}^n-φ_{i-1,j}^n)/2Δx+V(φ_{i,j+1}^n-φ_ {i,j-1}^n)/2Δy)其中φ_i^n表示第(i,j)个网格点在时间步n的浓度值,Δx和Δy分别表示网格在x和y方向上的空间步长,Δt表示时间步长。


tvd格式对流扩散方程解释说明1. 引言1.1 概述对流扩散方程是描述物质传输中对流和扩散过程的数学模型,广泛应用于自然科学和工程领域。
为了准确地求解对流扩散方程,需要选择适当的数值方法。
TVD(Total Variation Diminishing)格式是一种被广泛应用于求解对流扩散方程的数值方法,具有一阶或高阶精度、小量级能量损失等优点。
1.2 文章结构本文分为五个部分来讨论TVD格式与对流扩散方程。
首先,在引言部分概述了文章的背景和主要内容。
其次,在第二部分将简要介绍TVD格式和对流扩散方程,并探讨了TVD格式在解决对流扩散方程中的应用。
接下来,在第三部分详细介绍了TVD格式的原理和推导过程,还讨论了TVD限制器的作用和选择方法。
第四部分将通过数值实验和应用案例的分析,深入研究TVD格式的效果,并探讨其在实际问题中的应用意义。
最后,在第五部分总结本文研究工作并给出未来研究方向展望。
1.3 目的本文的主要目的是介绍TVD格式在求解对流扩散方程中的应用,并探讨其原理和推导过程。
希望通过数值实验和应用案例分析,验证TVD格式的有效性,同时提出改进方法。
本文还将总结研究工作的贡献点,并展望未来在这一领域的深入研究方向。
通过本文的撰写,旨在增加人们对TVD格式与对流扩散方程相关知识的了解,并为相关领域研究者提供参考和启示。
以上是“1. 引言”部分内容,包括概述、文章结构以及目的三个小节。
下文将继续详细阐述其他部分内容。
2. TVD格式与对流扩散方程2.1 TVD格式简介TVD(Total Variation Diminishing)格式是求解对流扩散方程的一种数值方法。
它在处理具有激烈变化、激波或阶跃的解时表现出色,并且能够有效地抑制数值耗散和震荡现象。
TVD格式广泛应用于流体力学、传热学等领域中。
2.2 对流扩散方程概述对流扩散方程是描述一维物理过程中物质输运的数学模型。
它由对流项和扩散项组成,其中对流项描述了物质通过速度场的输运,而扩散项则描述了物质因浓度或温度差异而发生的不规则传播。

一类二维稳态对流——扩散方程的有限差分法一维稳态扩散方程描述了物质在一维空间中的扩散行为。
然而,在某些情况下,我们需要研究物质在二维平面中的扩散行为,例如热传导、流体传输等。
本文将介绍一类二维稳态对流-扩散方程的有限差分法。
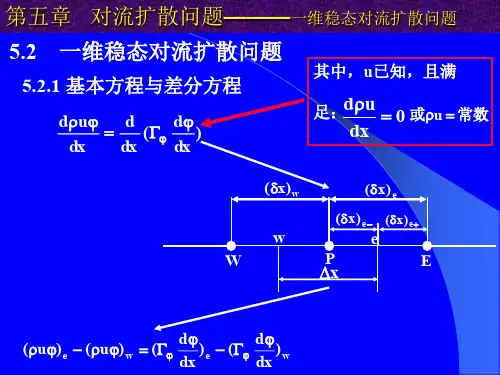
二维稳态对流-扩散方程可以写作:∇·(D∇u) + ∇·(cu) + fu = 0 —— (1)其中,D是扩散系数,c是速度场,u是待求解的物理量,f是源项。
在这个方程中,第一项表示物质的扩散项,第二项表示对流项,第三项表示源项。
我们需要求解方程(1),找到u的分布。
为了应用有限差分法来求解二维稳态对流-扩散方程,需要将二维空间离散化为一个网格。
假设我们将x方向离散为Nx个等距的节点,y方向离散为Ny个等距的节点,那么我们可以得到一个(Nx+1)×(Ny+1)的网格。
我们在网格节点上定义未知量u,然后将方程(1)对节点处的u进行离散化。
首先,我们对方程(1)的扩散项进行离散化。
我们使用五点差分格式来近似二维Laplace算符∇·(D∇u)。
对于网格节点(x,y),我们可以得到以下差分格式:(Dij(xi+1,yj)ui+1,j + Dij(xi-1,yj)ui-1,j +Dij(xi,yj+1)ui,j+1 + Dij(xi,yj-1)ui,j-1 -4Dij(xi,yj)ui,j) / ∆x^2 + (Dij(xi,yj)ui,j) / ∆y^2其中,∆x和∆y是网格步长,Dij是扩散系数。
接下来,我们对方程(1)的对流项进行离散化。
我们使用中心差分格式来近似二维梯度算符∇·(cu)。
对于网格节点(x,y),我们可以得到以下差分格式:(cxi+1/2,yj(ui+1,j - ui,j)) / ∆x + (cxi-1/2,yj(ui,j - ui-1,j)) / ∆x + (cyi,j+1/2(ui,j+1 - ui,j)) / ∆y + (cyi,j-1/2(ui,j - ui,j-1)) / ∆y其中,cxi+1/2,yj、cxi-1/2,yj、cyi,j+1/2和cyi,j-1/2是速度场在节点(x,y)处的中心点处的x和y分量。


一维对流扩散方程是描述物质传输和扩散现象的重要数学模型,对于工程、地质、生物等领域具有重要的理论和应用价值。
在科学研究和工程实践中,人们经常需要利用计算机软件对一维对流扩散方程进行数值求解,以获得物质传输和扩散的详细信息。
MATLAB作为一种强大的科学计算软件,提供了丰富的数学工具和编程接口,可以方便地对一维对流扩散方程进行数值求解。
本文将介绍利用MATLAB对一维对流扩散方程进行数值求解的基本方法和步骤。
一、一维对流扩散方程的数学模型一维对流扩散方程是描述物质在一维空间中传输和扩散的数学模型,通常可以写成如下的形式:∂c/∂t + u∂c/∂x = D∂^2c/∂x^2其中,c是物质浓度,t是时间,x是空间坐标,u是对流速度,D是扩散系数。
该方程的求解可以得到物质浓度随时间和空间的变化规律,对于理解物质传输和扩散过程具有重要意义。
二、MATLAB求解一维对流扩散方程的基本步骤在MATLAB中,可以利用偏微分方程求解工具箱(Partial Differential Equation Toolbox)来对一维对流扩散方程进行数值求解。
求解的基本步骤如下:1. 网格的生成首先需要在空间上生成一个网格,将一维空间离散化为有限个网格点。
可以利用MATLAB中的linspace函数或者自定义函数来实现网格的生成。
2. 边界条件和初始条件的设定根据具体问题的边界条件和初始条件,需要在MATLAB中对边界条件和初始条件进行设定。
3. 偏微分方程的建立利用MATLAB中的偏微分方程建立工具箱,可以方便地将一维对流扩散方程建立为MATLAB中的偏微分方程对象。
4. 方程的数值求解利用MATLAB中的求解器对建立的偏微分方程进行数值求解,可以获得一维对流扩散方程的数值解。
5. 结果的可视化可以利用MATLAB中丰富的绘图函数,对求解得到的数值解进行可视化,以便对物质传输和扩散过程进行直观的理解。
三、MATLAB求解一维对流扩散方程的举例为了进一步说明MATLAB求解一维对流扩散方程的方法,下面举一个简单的例子进行说明。
对流扩散方程是描述传质和动量传递的数学模型,在许多工程和科学领域都有广泛的应用。
Matlab作为一种强大的科学计算工具,具有丰富的函数库和灵活的编程环境,非常适合用来求解对流扩散方程。
本文将介绍在Matlab中求解对流扩散方程的基本方法,并提供一些实际案例来说明其应用。
一、对流扩散方程的基本形式对流扩散方程是描述物质在流体中输运的偏微分方程,其一般形式可以表示为:∂c/∂t + ∇·(uc) = ∇·(D∇c)其中c是物质的浓度,t是时间,u是流体的速度场,D是扩散系数。
这个方程同时考虑了对流和扩散的影响,描述了物质浓度随时间和空间的变化规律。
二、Matlab中求解对流扩散方程的基本步骤在Matlab中求解对流扩散方程的一般步骤如下:1.建立数学模型:根据实际问题建立对流扩散方程的数学模型,明确方程中的各个参数和边界条件。
2.离散化:将对流扩散方程进行离散化处理,常用的方法有有限差分法、有限元法和有限体积法等。
3.编写程序:利用Matlab的编程功能,编写求解对流扩散方程的程序,包括离散化方程、设置边界条件和时间步长等。
4.求解方程:利用Matlab的数值计算功能,对离散化后的对流扩散方程进行求解,得到数值解。
5.分析结果:对求解得到的数值解进行后处理,分析物质浓度随时间和空间的变化规律,得出有关问题的结论。
三、Matlab中求解对流扩散方程的实际案例下面通过一个实际案例来说明在Matlab中求解对流扩散方程的具体方法。
案例:地下水污染扩散模拟假设地下水中存在一种有害物质,通过对流扩散方程的数学建模和离散化处理,可以得到如下形式的离散方程:c(i,j,k+1) = c(i,j,k) + Δt[(u(i+1,j) - u(i,j))/Δx + (v(i,j+1) - v(i,j))/Δy] - Δt(D(i,j)/Δx^2(c(i+1,j,k) - 2c(i,j,k) + c(i-1,j,k)) +D(i,j)/Δy^2(c(i,j+1,k) - 2c(i,j,k) + c(i,j-1,k)))其中c(i,j,k)是第k个时间步长时点(i,j)处的浓度,u(i,j)和v(i,j)分别是流体的水平和垂直速度分量,D(i,j)是(i,j)处的扩散系数,Δx和Δy分别是网格的水平和垂直间距。
对流扩散方程有限差分方式求解对流扩散方程的差分格式有很多种,在本节中将介绍以下3种有限差分格式:中心差分格式、Samarskii 格式、Crank-Nicolson 型隐式差分格式。
3.1 中心差分格式时刻导数用向前差商、空间导数用中心差商来逼近,那么就取得了(1)式的中心差分格式]6[21111122h u u u vhu u au u nj n j n j nj n j n jn j -+-+++-=-+-τ(3)假设令 haτλ=,2h vτμ=,那么(3)式可改写为)2()(2111111nj n j n j n j n j n j n j u u u u u u u -+-+++-+--=μλ (4)从上式咱们看到,在新的时刻层1+n 上只包括了一个未知量1+n j u ,它能够由时刻层n 上的值n j u 1-,n j u ,n j u 1+直接计算出来。
因此,中心差分格式是求解对流扩散方程的显示格式。
假定),(t x u 是定解问题的充分滑腻的解,将1+n j u ,n j u 1+,nj u 1-别离在),(n j t x 处进行Taylor 展开:)(),(),(211ττO t u t x u t x u unjn j n j n j+⎥⎦⎤⎢⎣⎡∂∂+==++)(2),(),(322211h O x u h x u h t x u t x u u nj nj n j n j n j +⎥⎦⎤⎢⎣⎡∂∂+⎥⎦⎤⎢⎣⎡∂∂+==++ )(2),(),(322211h O x u h x u h t x u t x u u njnj n j n j n j +⎥⎦⎤⎢⎣⎡∂∂+⎥⎦⎤⎢⎣⎡∂∂-==--代入(4)式,有 21111122),(hu u u vhu u au u t x T nj n j n j nj n j n jn j n j -+-+++---+-=τ)()()(2222h O v x u v h O a x u a O t u nj nj nj ⋅-⎥⎦⎤⎢⎣⎡∂∂-⋅+⎥⎦⎤⎢⎣⎡∂∂++⎥⎦⎤⎢⎣⎡∂∂=τ )()()(222h O v a O x u v x u a t u njnj nj ⋅-++⎥⎦⎤⎢⎣⎡∂∂-⎥⎦⎤⎢⎣⎡∂∂+⎥⎦⎤⎢⎣⎡∂∂=τ )(2h O +=τ显然,当0→τ,0→h 时,0),(→n j t x T ,即中心差分格式与定解问题是相容的。