第五章对流扩散方程
- 格式:pdf
- 大小:351.46 KB
- 文档页数:28


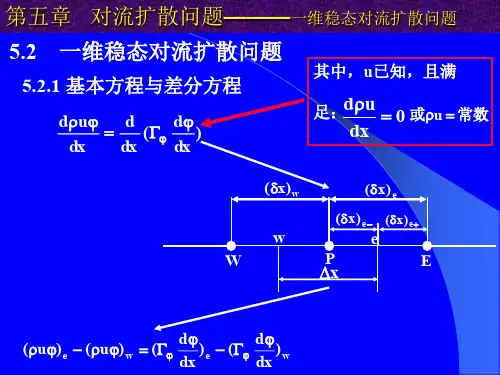

对流扩散方程解析解对流扩散方程(Convection-DiffusionEquation,CDE)是描述物理系统中物质扩散和热对流运动的方程。
它源于20世纪30年代真空磁体理论中发现的电子运动方程,在50年代被普及应用于各种工程、物理学和化学领域,如电子、热传输、水力学等,具有不可缺少的重要意义。
一般来说,对流扩散方程可以被描述为:$$frac{partial y}{partial t}=afrac{partial^2 y}{partial x^2}+bfrac{partial y}{partial x}+cfrac{partial y}{partial y}+d$$其中,a、b、c和d是常数,t和x分别代表时间和物理位置。
若把空间坐标投射到它们的平面上,则可以用更具体的形式表述为: $$frac{partial y}{partial t}=afrac{partial^2 y}{partial x^2}+bfrac{partial y}{partial x}+cfrac{partial y}{partial y}+d+frac{partial y}{partial z}$$其中,z是投射后的空间坐标,a、b、c和d也可以改变以适合不同的实际应用场景。
对于对流扩散方程的解析解,有两种基本方法:一种是用不定积分法;另一种是用微分平面法,也称作渐进分析方法。
从一般的原理上来看,不定积分法是把对流扩散方程拆解成多个简单的可求解的微分方程,然后分别求解它们,最后再综合求得总解。
此外,它还可以运用标准积分法来近似求解,特别有利于解复杂的多变量方程。
而渐进分析(Perturbation Analysis)是把复杂的问题划分成几个渐进步骤,每一步把问题简化为可以近似解决的状态,依此不断迭代,最终求得近似解。
这种技术通常用来求解非线性方程,对于对流扩散方程求解也非常有效,能有效地提高准确度和计算速度。
此外,还有其他一些求解方法,比如拉格朗日法(Lagrange Method)、拉普拉斯正则化(Laplace Regularization)以及偏微分方程的泛函理论方法(Functional Theory of Partial Differential Equations)等。


输运方程对流扩散方程输运方程是描述物质传输过程的数学模型,常见的有对流扩散方程。
对流扩散方程是由对流和扩散两种机制共同产生的输运过程来描述的,它的一般形式为:∂c/∂t+∇·(v*c)=∇·(D*∇c)其中,c表示物质的浓度或者响应变量,t表示时间,v表示流体的速度场,D表示物质的扩散系数,∇表示梯度运算符。
对流项描述了物质的对流运动,即物质随着流体的移动而移动。
对于三维坐标系来说,对流项可以表示为∇·(v*c)。
具体来说,对流项的每一项分别表示了物质在x、y和z方向上的携带速度与浓度梯度的乘积。
扩散项描述了物质由浓度高处至浓度低处的扩散现象,即物质自发性地从高浓度区域向低浓度区域传播。
扩散项可以表示为∇·(D*∇c),其中D是扩散系数,表示物质扩散的速率与浓度梯度的乘积。
对流扩散方程的物理意义是描述了物质在流体中传输的速率与物质浓度梯度之间的关系。
通过对流项,方程能够描述物质随着流体的运动快速传输的现象;而通过扩散项,方程能够描述物质由浓度高处向浓度低处传输的现象。
综合考虑对流和扩散的作用,对流扩散方程能够比较准确地描述物质在流体中的传输过程。
对流扩散方程在科学和工程领域有广泛的应用。
例如,在污染物传输和扩散模拟中,对流扩散方程可用于描述污染物由源区到周围空气或水体的传输过程。
在热传导模拟中,对流扩散方程可用于描述热量由高温区域到低温区域的传导过程。
在物质传递过程中,对流扩散方程也被广泛应用于描绘物质的传输行为。
总结起来,对流扩散方程是一种常见的输运方程,它能够描述物质由流体传输并扩散的过程。
通过对流项和扩散项的综合作用,对流扩散方程能够比较准确地描述物质在流体中的传输行为,所以在科学和工程领域有着广泛的应用。

对流扩散方程clank标题:对流扩散方程的概述引言概述:对流扩散方程是数学中常见的描述物质传输过程的方程。
它在众多领域中都有广泛的应用,如流体力学、热传导、质量传输等。
本文将从五个大点出发,详细阐述对流扩散方程的相关内容。
正文内容:1. 对流扩散方程的基本概念1.1 对流扩散方程的定义1.2 对流扩散方程的一般形式1.3 对流扩散方程的物理意义2. 对流项与扩散项的影响2.1 对流项的作用2.2 扩散项的作用2.3 对流项与扩散项的相互作用3. 对流扩散方程的解析解与数值解3.1 解析解的求解方法3.2 数值解的求解方法3.3 解析解与数值解的比较4. 对流扩散方程的边界条件和初值条件4.1 边界条件的选择与影响4.2 初值条件的确定与影响4.3 边界条件和初值条件的耦合效应5. 对流扩散方程的应用领域5.1 流体力学中的应用5.2 热传导中的应用5.3 质量传输中的应用总结:对流扩散方程是描述物质传输过程的重要方程,其基本概念包括方程的定义、形式和物理意义。
对流项和扩散项是方程中的两个关键因素,它们分别对物质传输起到对流和扩散的作用,并且相互作用影响着传输过程。
对流扩散方程的求解可以采用解析解和数值解两种方法,它们各有优劣,需要根据具体情况选择。
边界条件和初值条件是方程求解中必要的条件,它们的选择与确定对结果有重要影响。
对流扩散方程在流体力学、热传导和质量传输等领域都有广泛应用,它为我们理解和解决实际问题提供了重要的数学工具。
总之,对流扩散方程是一个复杂而重要的数学方程,它在物质传输过程中起着关键作用。
深入理解和研究对流扩散方程,对于解决实际问题具有重要意义。

对流扩散方程ν22u u ua t x x抖 +=抖¶ 网格比λt a x D =D , ν2t r xD =D 而它们的比值λνν2t a a x x r t x D D D ==D D 是一个无量纲量,称为网格雷诺数,也就是以网格尺寸 x D 为特征长度的雷诺数,通常记作 Re x D 。
(1) 显式中心差分格式ν11111222n nn nn n nj jj j j j j u u u u u u u atxx++-+----++=D D D即()()λ1111122n n nn n n nj jj j j j j u u u u r u u u ++-+-=--+-+ 精度:()O 2 , n j R t x =D D稳定性分析:设 jikx n nj k C eε= ,则()1j ik x xn n j k C e ε-D -= ,()ε1j ik x xn n j k C e+D += ,11jikx n n j k C eε++=代入差分格式()()()()λ122jj jj j j j ik x xik x xikx ikx n n n n kkk kik x x ik x x ikx n n n k k k Ce C eC e C er C e C e C e +D -D ++D -D 骣÷ç=--÷ç桫骣÷ç+-+÷ç桫令 k x α=D ,可求出增长因子()()()ααααλλαααααλ121221sin 2cos 114sin 2sin cos 222n k nk i i i i C G C e e r e e i r r i +--==--+-+=-+-骣骣鼢珑鼢=-+珑鼢珑鼢桫桫所以αααλααααλαααλ22222242222222214sin 2sin cos 22218sin16sin4sincos22221424sin cos sin 222G r r r r r 骣骣鼢珑鼢=-+珑鼢珑鼢桫桫=-++骣÷ç÷=---ç÷ç÷桫因此ααλ222221 124sin cos 022G G r r [[--我们来考虑函数()αααλ222224sin cos 22f r r =--的极值。
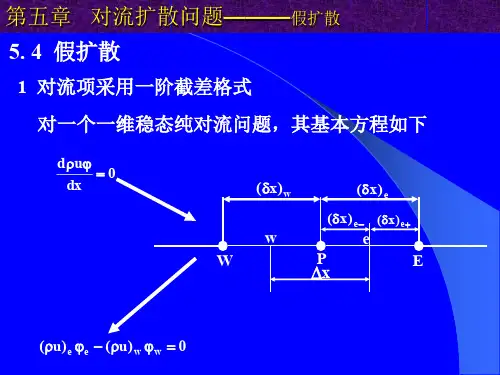


对流扩散方程解析解对流扩散方程(Convection-DiffusionEquation)是在求解流体,如气体或液体的输运问题时需要使用的普通微分方程。
它表示物质被三种因素作用所引起的质量流动:对流、扩散和反应。
在本文中,我们将讨论对流扩散方程的解析解,以及它在工程中的重要作用。
首先,要理解对流扩散方程,我们必须从它的数学形式开始。
它可以用以下形式表示:$$frac{partial c}{partial t}+ vec{u} cdotabla c-Dabla^2 c=R$$在这里,$c$表示物质的浓度,$vec{u}$表示流体的速度,$D$表示物质的扩散系数,$R$表示反应的密度。
对流扩散方程的解析解是一种运用数学方法来求解这个方程的方法。
它主要是利用积分变换法(Integral Transform Method),将复杂的运动学问题转化为一组常微分方程求解。
解析解方法在解决一定类型的常微分方程时尤其有用,特别是当一个系统的边界条件是确定的时。
解析解的优势在于它可以提供直观的解,方便比较和评估结果,便于理解物理机理。
它也可以提供准确的结果,并可以用于组合的求解方法中。
在工程领域,对流扩散方程解析解的应用非常重要。
它可以被应用于温度或物质浓度输运,以及其他类似现象的计算。
例如,对流扩散方程可以用来模拟一定范围内扩散方式的热量传输,从而推测温度场分布;也可以用来模拟入口流场和出口的物质浓度的变化;它还可以用来描述各种物质在工程系统内的扩散问题。
再者,解析解方法也被广泛应用于制药行业。
对流扩散方程可以用来模拟药物在体内的运动,从而计算出最佳控制方案,以达到药物最佳疗效。
这不仅可以为药物分布模型提供依据,还可以用来估算药物组分以及药物与体细胞的相互作用等工程相关问题,从而帮助制药公司最大程度地提高药品安全性和疗效。
最后,对流扩散方程的解析解是一种非常有效的数学方法,它可以帮助我们更加清晰地理解流体输运问题,并可以提供准确可靠的结果。
对流扩散方程
1 流体扩散方程
流体扩散方程是一个历史悠久、解决常见力学概念的重要方法和
工具,它可以定量衡量复杂流体在双向运动和定向变化中经历的变化。
因此,它被广泛应用于流体动力学,比如在水动力和海洋动力学中。
2 原理
流体扩散方程基于小块体强迫传播的假定,从力学上讲,它是一
种可以解释流体物质的收支问题的方程。
由于流体受到外部力的影响,对某一点的流体运动行为可以用某种单元强迫块的形式进行观察,而
该点的微量物质的多元流变形式可以通过该块的公式来表示。
3 表达式
流体扩散方程的表达式如下:
$$\frac{\partial f}{\partial t}+ \vec{u} \cdot \nabla f = D \nabla^{2} f$$
其中:
$f$是流体属性函数;$\vec{u}$是流体速度;t是时刻;
$\nabla$和$\nabla{2}$是偏导数和二阶导数全称;D表示流体扩散率。
4 应用
流体扩散方程的应用广泛,可以解决流体运动与转移复杂问题。
比如在海洋科学中,它可以用来研究海洋的水文特征;在水力学中,
可以用来模拟水位和洪水洪峰等问题;在大气学领域,可以用来描述
大气给热扩散等问题;在机械工程中,可以模拟非稳定流、结构层HTML等问题。
5 结论
流体扩散方程是一种研究流体运动和转移问题的重要工具,它可
以分析流体行为,以便为设计解决复杂的流体问题提供有价值的答案。
此外,流体扩散方程也被应用于一些现实问题,例如气象学和机械工
程中的装配问题。
主讲陶文铨西安交通大学能源与动力工程学院热流中心CFD-NHT-EHT CENTER2010年10月18日, 西安数值传热学第五章对流扩散方程的离散格式(2)对流项离散格式的重要性及两种离散方式5.5.1假扩散的含义与成因5.5.2一阶截差格式引起严重假扩散举例1.本来的含义2.扩充的含义3.Taylor 展开法的分析5.5关于假扩散的讨论5.5.3网格倾斜交叉引起的计算误差5.5.4 非常数源项引起的假扩散5.5.5 两个名例以一维非稳态纯对流过程为例俩分析,其中有两n nφφ2(,O x φΔΔ其中关于时间的二阶导数项可做如下变化:时才没有这部分的计算误差。
2. 扩充的含义现有文献中常常将较大的计算误差都称为假扩散,大致有以下几项原因:(1) 一阶导数的一阶截差格式;(2) 流动方向与网格线呈倾斜交叉;(3) 离散格式未计及非常数源项的影响。
5.5.2一阶截差格式引起严重假扩散举例1.一维稳态对流扩散问题对流项用FUD,扩散项用CD,当Pe较大时,数值计算结果严重偏离精确解。
Physically plausible solution纯对流传递纯对流传递由离散方程:1n−1此时只有对流,没有扩散!时则有严重假扩散!0.8C =0.8C =当时,产生了严重的扩散作此种误差称为流向假扩散Γ≠Γ气流01. 设UE对P 控制容积,有2. 设控制容积,此时:计算误差纯对流传递三个对流问题的归纳这就是假扩散纯对流传递3)网格倾斜交叉引起的计算误差E冷热流体之间产生了温度均匀化的过程,即交叉5.5.5 已知流场计算温度场232(1),2(1)u y x v x y =−=−−参考解xT严重假扩散2) Leonard细高方腔中的自然对流换热5.6.1采用高阶格式克服流向假扩散5.6可以克服或减轻假扩散的格式与方法5.2.2 克服、减轻交叉假扩散的方法1. 采用二阶迎风2.采用三阶迎风3. 采用QUICK 格式1. 采用有效扩散系数2.采用自适应网格4. 采用SGSD 格式可以克服或减轻假扩散的格式与方法相当于界面上的中心差分)W WWxφ+Δ如型线上凹,则(2) FVM向上游取两点定义界面插值2.采用三阶迎风展开定义-一阶导数的三阶偏差分格式3. 采用定义-界面的插值在中心差分基础上考虑曲中心差分插值率修正?需要满足两个条件:插值的正确修正:相邻(2)0W PE φφφ−+<型线下凹8Cur −对e-界面u e 小于零时,取,,W P φφφu e 大于零时,取怎样相邻的三点?QUICK(2)e φφ=1/2w i φφ−=有:4. 采用CD条件稳定,但没有二阶假扩散;二阶迎风绝对稳定,组合起来,但是:如何确定值,特别是如何由计算结果来5. 高阶格式实施中的问题f u f计算边界:固o2) 代数方程的求解:等时,5.6.2用减小扩散系采用自适应网格(以减轻流5.7 对流-扩散方程离散形式稳定性分析5.7.1 数值计算中常见的三种不稳定性5.7.2 分析对流项格式不稳定性的“符号不变原则”5.7.3 稳定性分析结果讨论5.7.4 对流项格式问题讨论小结2.“符号不变”原则的基本思想3. “符号不变”原则的实施步骤4. “符号不变”原则的实施例子1. 研究背景扩散方程离散形式稳定性分析也会产生振荡的解,称为对流项离散格式的不稳态定性,研究目的是,找出产生振荡的临界Peclet 数。
对流扩散方程推导过程对流扩散方程是描述物质在流体中传输的数学模型。
它可以用来描述物质的浓度、温度、速度等在流体中的传播过程。
本文将从推导过程的角度,详细介绍对流扩散方程的推导过程。
我们考虑一维情况下的对流扩散方程。
假设物质在流体中的传输速度为u,浓度为C,扩散系数为D。
根据质量守恒定律,我们可以得到物质的传输速度和扩散速度之和等于物质的净传输速度。
接下来,我们考虑扩散的部分。
根据菲克定律,扩散速度与浓度梯度成正比,扩散的方向是从浓度高的地方向浓度低的地方传播。
因此,扩散的速度可以表示为-D乘以浓度的梯度。
然后,我们考虑对流的部分。
对流是由流体的流动引起的物质传输。
对于一维情况,对流的速度可以表示为u乘以浓度的梯度。
需要注意的是,对流速度的正负取决于流动的方向。
综合考虑扩散和对流,我们可以得到一维情况下的对流扩散方程:∂C/∂t + u*∂C/∂x = D*∂^2C/∂x^2其中∂C/∂t表示时间对浓度的偏导数,∂C/∂x表示空间对浓度的偏导数,∂^2C/∂x^2表示浓度的二阶空间导数。
接下来,我们考虑二维情况下的对流扩散方程。
假设物质在流体中的传输速度为(u,v),浓度为C,扩散系数为D。
同样根据质量守恒定律,我们可以得到物质的传输速度和扩散速度之和等于物质的净传输速度。
对于扩散部分,我们仍然可以应用菲克定律,扩散速度与浓度梯度成正比。
因此,扩散的速度可以表示为-D乘以浓度的梯度。
对于对流部分,我们需要考虑两个方向上的流动速度。
对流的速度可以表示为(u,v)乘以浓度的梯度。
需要注意的是,对流速度的正负取决于流动的方向。
综合考虑扩散和对流,我们可以得到二维情况下的对流扩散方程:∂C/∂t + u*∂C/∂x + v*∂C/∂y = D*(∂^2C/∂x^2 + ∂^2C/∂y^2)其中∂C/∂t表示时间对浓度的偏导数,∂C/∂x和∂C/∂y表示空间对浓度的偏导数,∂^2C/∂x^2和∂^2C/∂y^2表示浓度的二阶空间导数。
对流扩散方程及其解法对流扩散方程是物理学中最常见的一类偏微分方程,与流体力学、传热传质学等学科密切相关。
解析求解对流扩散方程可以揭示物理现象的本质,并在实际应用中提供有效的工程计算方法。
一、对流扩散方程对流扩散方程是将扩散项和对流项结合在一起的偏微分方程,一般形式如下:$$\dfrac{\partial u}{\partial t} = D\dfrac{\partial^2 u}{\partial x^2} - v\dfrac{\partial u}{\partial x} + f(x,t)$$其中 $u$ 是未知函数,$D$ 是扩散系数,$v$ 是速度场,$f(x,t)$ 是源项。
对流扩散方程描述了时间 $t$ 和空间 $x$ 上的某一物理量 $u$ 随时间的变化规律。
二、对流项与扩散项对流扩散方程中的对流项和扩散项代表不同的物理过程,互相作用形成物理现象。
对流项描述了物质由一点向另一点的移动,通常由质量流或者粒子流的线性变化来表示。
扩散项描述了物质的热或质量分布率随空间位置的二次变化。
对流项和扩散项的比值通常称为对流性能。
三、有限差分方法有限差分法是对流扩散方程的求解方法之一,将空间和时间的连续域离散化成离散点,并通过有限差分逼近偏微分方程的微分项,从而转化成一个代数问题。
常见的有限差分格式有向后差分法、向前差分法、中心差分法等。
假设在 $(x_i,t_n)$ 的数值解已知,设网格步长为 $\Delta x$ 和$\Delta t$,则有:$$u(x_i,t_{n+1}) \approx u(x_i,t_{n}) + \Delta tf(u(x_i,t_n),x_i,t_n)$$其中 $f(u(x_i,t_n),x_i,t_n)$ 是对流扩散方程右端的非线性项。
将$u(x_i,t_n)$ 用它四周的$u(x_{i-1},t_n)$、$u(x_{i+1},t_n)$、$u(x_i,t_{n-1})$ 替代,可以得到向后差分格式:$$u(x_i,t_{n+1}) \approx u(x_i,t_{n}) + D\dfrac{\Delta t}{\Deltax^2}[u(x_{i+1},t_n) - 2u(x_i,t_n) + u(x_{i-1},t_n)]-v\dfrac{\Deltat}{\Delta x}[u(x_{i+1},t_n) - u(x_{i-1},t_n)] + \Delta tf(u(x_i,t_n),x_i,t_n)$$四、求解方法对流扩散方程的解法包括解析解和数值解,主要取决于方程的形式和边界条件的选取。