对流扩散方程

水-沉积物界面物质的浓度梯度计算一、引言水-沉积物界面是自然界中重要的地质、生物和化学过程发生的场所。

在这个界面上，水中的溶质会通过扩散和对流的方式进入沉积物中，而沉积物中的溶质也会通过扩散和对流的方式进入水中。

了解水-沉积物界面物质浓度梯度的特征对于理解和预测环境中的污染物迁移、生态系统的健康状态以及地质过程的发展具有重要意义。

二、水-沉积物界面物质浓度梯度的计算方法1. 扩散通量法扩散通量法是计算水-沉积物界面物质浓度梯度的常用方法。

根据菲克定律，溶质的扩散通量可以通过以下公式计算：J = -D*(dc/dx)其中，J是扩散通量，D是扩散系数，dc/dx是物质浓度随距离的梯度。

2. 对流扩散方程法对流扩散方程法结合了对流和扩散的作用，可以更准确地描述水-沉积物界面物质的迁移过程。

对于一维情况，对流扩散方程可以写为：∂c/∂t = D*∂²c/∂x² - v*∂c/∂x其中，c是物质浓度，t是时间，D是扩散系数，v是速度，∂c/∂t是物质浓度随时间的变化率，∂²c/∂x²是物质浓度随距离的二阶导数，∂c/∂x是物质浓度随距离的梯度。

三、水-沉积物界面物质浓度梯度的环境应用1. 污染物迁移预测通过计算水-沉积物界面物质浓度梯度，可以预测污染物在水和沉积物之间的迁移过程。

根据浓度梯度的方向和大小，可以评估污染物的迁移速率和范围，为环境保护和污染治理提供科学依据。

2. 生态系统健康评估水-沉积物界面是生态系统中物质交换的重要界面。

通过测定水-沉积物界面物质浓度梯度，可以评估生态系统中物质循环的状态和健康状况。

高浓度梯度可能对生态系统产生负面影响，而低浓度梯度可能表明生态系统的健康状态良好。

3. 地质过程研究水-沉积物界面物质浓度梯度的计算可以帮助研究地质过程中的物质迁移和沉积过程。

例如，通过测量水-沉积物界面的铁、锰等金属元素的浓度梯度，可以了解地下水中金属元素的来源和转化过程，进而揭示地球内部的地质活动和地质历史。

对流扩散方程解析解对流扩散方程(Convection-DiffusionEquation,CDE)一类傅里叶方程，用于研究物理系统中物质的运动行为。

它通常用来解释流体或溶液在空间和时间内的扩散过程。

这类方程可以通过求解数学解析解来进行解，也可以使用数值解，如有限元等进行解算。

对流扩散方程的推导可以从推导物理系统的分量开始。

在一个包含温度、速度和浓度的物理系统中，我们可以认为这些物质的变化是由守恒定律和扩散定律推导出来的，从而形成了一般的对流扩散方程。

对流扩散方程的一般形式为：$$frac{partial{boldsymbol{u}}}{partial{t}} +ablacdot(boldsymbol{u} otimes boldsymbol{u}) -abla cdot left(xiablaboldsymbol{u} right) = boldsymbol{S}$$其中，$boldsymbol{u}$表示物理量，$t$表示时间，$xi$表示扩散系数。

$boldsymbol{S}$表示物理量的源。

例如，在某个区域内，如果有物质被外界源消耗掉，$boldsymbol{S}$的值就会变小。

对于一般的对流扩散方程，我们可以分解出一个动能方程和一个扩散方程来进行解算：动能方程：$$frac{partial{boldsymbol{u}}}{partial{t}} +ablacdot(boldsymbol{u} otimes boldsymbol{u}) = boldsymbol{S}$$扩散方程：$$abla cdot (xiablaboldsymbol{u}) = 0$$解决对流扩散方程的解析解有几种方法，其中最常用的是求解Laplace换和 Laplace阵。

Laplace换是对一个函数 $f(t)$变换，用 Laplace换将$f(t)$换成 $F(s)$形式，其中，$s$ Laplace换的参数。

对流扩散方程解析解对流扩散方程（Convection-DiffusionEquation，CDE）是描述物理系统中物质扩散和热对流运动的方程。

它源于20世纪30年代真空磁体理论中发现的电子运动方程，在50年代被普及应用于各种工程、物理学和化学领域，如电子、热传输、水力学等，具有不可缺少的重要意义。

一般来说，对流扩散方程可以被描述为：$$frac{partial y}{partial t}=afrac{partial^2 y}{partial x^2}+bfrac{partial y}{partial x}+cfrac{partial y}{partial y}+d$$其中，a、b、c和d是常数，t和x分别代表时间和物理位置。

若把空间坐标投射到它们的平面上，则可以用更具体的形式表述为： $$frac{partial y}{partial t}=afrac{partial^2 y}{partial x^2}+bfrac{partial y}{partial x}+cfrac{partial y}{partial y}+d+frac{partial y}{partial z}$$其中，z是投射后的空间坐标，a、b、c和d也可以改变以适合不同的实际应用场景。

对于对流扩散方程的解析解，有两种基本方法：一种是用不定积分法；另一种是用微分平面法，也称作渐进分析方法。

从一般的原理上来看，不定积分法是把对流扩散方程拆解成多个简单的可求解的微分方程，然后分别求解它们，最后再综合求得总解。

此外，它还可以运用标准积分法来近似求解，特别有利于解复杂的多变量方程。

而渐进分析（Perturbation Analysis）是把复杂的问题划分成几个渐进步骤，每一步把问题简化为可以近似解决的状态，依此不断迭代，最终求得近似解。

这种技术通常用来求解非线性方程，对于对流扩散方程求解也非常有效，能有效地提高准确度和计算速度。

此外，还有其他一些求解方法，比如拉格朗日法（Lagrange Method）、拉普拉斯正则化（Laplace Regularization）以及偏微分方程的泛函理论方法（Functional Theory of Partial Differential Equations）等。

输运方程对流扩散方程输运方程是描述物质传输过程的数学模型，常见的有对流扩散方程。

对流扩散方程是由对流和扩散两种机制共同产生的输运过程来描述的，它的一般形式为：∂c/∂t+∇·(v*c)=∇·(D*∇c)其中，c表示物质的浓度或者响应变量，t表示时间，v表示流体的速度场，D表示物质的扩散系数，∇表示梯度运算符。

对流项描述了物质的对流运动，即物质随着流体的移动而移动。

对于三维坐标系来说，对流项可以表示为∇·(v*c)。

具体来说，对流项的每一项分别表示了物质在x、y和z方向上的携带速度与浓度梯度的乘积。

扩散项描述了物质由浓度高处至浓度低处的扩散现象，即物质自发性地从高浓度区域向低浓度区域传播。

扩散项可以表示为∇·(D*∇c)，其中D是扩散系数，表示物质扩散的速率与浓度梯度的乘积。

对流扩散方程的物理意义是描述了物质在流体中传输的速率与物质浓度梯度之间的关系。

通过对流项，方程能够描述物质随着流体的运动快速传输的现象；而通过扩散项，方程能够描述物质由浓度高处向浓度低处传输的现象。

综合考虑对流和扩散的作用，对流扩散方程能够比较准确地描述物质在流体中的传输过程。

对流扩散方程在科学和工程领域有广泛的应用。

例如，在污染物传输和扩散模拟中，对流扩散方程可用于描述污染物由源区到周围空气或水体的传输过程。

在热传导模拟中，对流扩散方程可用于描述热量由高温区域到低温区域的传导过程。

在物质传递过程中，对流扩散方程也被广泛应用于描绘物质的传输行为。

总结起来，对流扩散方程是一种常见的输运方程，它能够描述物质由流体传输并扩散的过程。

通过对流项和扩散项的综合作用，对流扩散方程能够比较准确地描述物质在流体中的传输行为，所以在科学和工程领域有着广泛的应用。

对流扩散方程clank标题：对流扩散方程的概述引言概述：对流扩散方程是数学中常见的描述物质传输过程的方程。

它在众多领域中都有广泛的应用，如流体力学、热传导、质量传输等。

本文将从五个大点出发，详细阐述对流扩散方程的相关内容。

正文内容：1. 对流扩散方程的基本概念1.1 对流扩散方程的定义1.2 对流扩散方程的一般形式1.3 对流扩散方程的物理意义2. 对流项与扩散项的影响2.1 对流项的作用2.2 扩散项的作用2.3 对流项与扩散项的相互作用3. 对流扩散方程的解析解与数值解3.1 解析解的求解方法3.2 数值解的求解方法3.3 解析解与数值解的比较4. 对流扩散方程的边界条件和初值条件4.1 边界条件的选择与影响4.2 初值条件的确定与影响4.3 边界条件和初值条件的耦合效应5. 对流扩散方程的应用领域5.1 流体力学中的应用5.2 热传导中的应用5.3 质量传输中的应用总结：对流扩散方程是描述物质传输过程的重要方程，其基本概念包括方程的定义、形式和物理意义。

对流项和扩散项是方程中的两个关键因素，它们分别对物质传输起到对流和扩散的作用，并且相互作用影响着传输过程。

对流扩散方程的求解可以采用解析解和数值解两种方法，它们各有优劣，需要根据具体情况选择。

边界条件和初值条件是方程求解中必要的条件，它们的选择与确定对结果有重要影响。

对流扩散方程在流体力学、热传导和质量传输等领域都有广泛应用，它为我们理解和解决实际问题提供了重要的数学工具。

总之，对流扩散方程是一个复杂而重要的数学方程，它在物质传输过程中起着关键作用。

深入理解和研究对流扩散方程，对于解决实际问题具有重要意义。

ns方程对流和扩散项
NS方程的对流项和扩散项分别如下：
1.对流项。

对流项是由拉格朗日描述法转为欧拉法而衍生出来的项。

这一转
变代表着从质量守恒的研究角度转为体积守恒的研究角度，或者可以看做从粒子的角度向场的角度转变。

从物理的角度讲，对流项通俗说就是速度运输速度自己，具体作用为加大速度梯度。

同时，对流项导致的mode
coupling也是能量在不同尺度间传递的重要因素。

2.扩散项。

扩散项由应力项化简而得。

NS方程是扩散对流方程的特殊形式，它们均与守恒律有关，是最基本的物理定理在数学上的直接反应。

对于部分教材直接从微元提出发导出NS方程的观点不是特别赞同。

比较现代的方法是先得到雷诺输运定理，再根据质量守恒定律和牛顿第二定律得到基本控制方程组1。

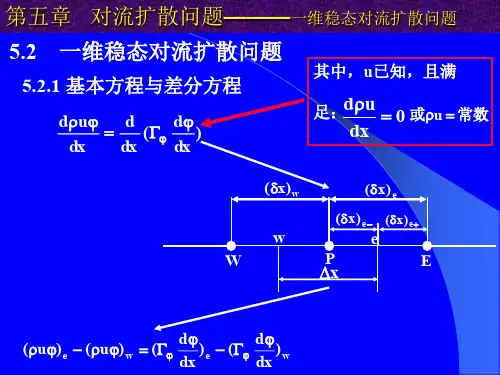
对流扩散方程解析解对流扩散方程（Convection-DiffusionEquation）是在求解流体，如气体或液体的输运问题时需要使用的普通微分方程。

它表示物质被三种因素作用所引起的质量流动：对流、扩散和反应。

在本文中，我们将讨论对流扩散方程的解析解，以及它在工程中的重要作用。

首先，要理解对流扩散方程，我们必须从它的数学形式开始。

它可以用以下形式表示：$$frac{partial c}{partial t}+ vec{u} cdotabla c-Dabla^2 c=R$$在这里，$c$表示物质的浓度，$vec{u}$表示流体的速度，$D$表示物质的扩散系数，$R$表示反应的密度。

对流扩散方程的解析解是一种运用数学方法来求解这个方程的方法。

它主要是利用积分变换法（Integral Transform Method），将复杂的运动学问题转化为一组常微分方程求解。

解析解方法在解决一定类型的常微分方程时尤其有用，特别是当一个系统的边界条件是确定的时。

解析解的优势在于它可以提供直观的解，方便比较和评估结果，便于理解物理机理。

它也可以提供准确的结果，并可以用于组合的求解方法中。

在工程领域，对流扩散方程解析解的应用非常重要。

它可以被应用于温度或物质浓度输运，以及其他类似现象的计算。

例如，对流扩散方程可以用来模拟一定范围内扩散方式的热量传输，从而推测温度场分布；也可以用来模拟入口流场和出口的物质浓度的变化；它还可以用来描述各种物质在工程系统内的扩散问题。

再者，解析解方法也被广泛应用于制药行业。

对流扩散方程可以用来模拟药物在体内的运动，从而计算出最佳控制方案，以达到药物最佳疗效。

这不仅可以为药物分布模型提供依据，还可以用来估算药物组分以及药物与体细胞的相互作用等工程相关问题，从而帮助制药公司最大程度地提高药品安全性和疗效。

最后，对流扩散方程的解析解是一种非常有效的数学方法，它可以帮助我们更加清晰地理解流体输运问题，并可以提供准确可靠的结果。

A对流扩散方程的求解对流扩散问题的有效数值解法一直是计算数学中重要的研究内容，求解对流扩散方程的数值方法主要是有限差分法(FDM)、有限元法(FEM)、有限体积法(FVM)、有限解析法(FAM)、边界元法(BEM)、谱方法(SM) 等多种方法。

但是对于对流占优问题，用通常的差分法或有限元法进行求解将出现数值震荡。

为了克服数值震荡，80年代，J.Douglas,Jr.和T.F.Russell 等提出特征修正技术求解对流扩散占优的对流扩散问题，与其它方法相结合，提出了特征有限元方法、特征有限差分方法、特征混合元方法；T.J.Hughes和A.Brooks提出过一种沿流线方向附加人工黏性的间断有限元法，称为流线扩散方法(SDM)。

有限差分法、有限元法、有限体积法是工程应用中的主要方法。

对流扩散方程的特点对流扩散方程右端第一项为扩散项，左端第二项则是对流项。

由于其方程本身的特点，给建立准确有效的数值求解方法带来一定的困难。

对流和扩散给流体中由流体携带的某种物理量的变化过程，可以通过一个无量纲的特征参数(Peclet数)来描述，Peclet数Pe的定义为：Pe=|ν|L/D。

这里v是来流速度，L是特征长度，D是物质的扩散系数。

如果Pe数较小，即对流效应相对较弱，这类问题中，扩散占主导地位，方程是椭圆型或抛物线型；如果Pe数较大，即溶质分子的扩散相对于流体速度而言是缓慢的，这类问题中，对流占优，方程具有双曲型方程的特点。

对于对流占优问题的求解，采用常规的Galerkin有限元方法，为了避免求解结果产生数值振荡，获得稳定解，则应使每个单元的局部Peclet数，Peh=|ν|h/D≤2，这里h为单元的最大尺寸，|v|为单元中的最大速度分量值。

因此，用本文方法求解对流占优对流扩散问题，要得到稳定解，则要通过加密有限元网格来实现。

对流扩散方程解析解对流扩散方程（Convection-DiffusionEquation）是流体动力学领域里一个基本的求解方程，它表示物理系统的流体流动特征，可用于模拟和分析气体的湍流流动、热力学和传热运算等问题。

新的求解方法对对流扩散方程的解析解具有重要意义。

对流扩散方程的一般形式为：$$frac{partial c}{partial t}+ucdotabla c-DDelta c=f$$其中，u表示大尺度的流体速度，D表示流体扩散系数，f表示质量源期（如，物质沉积或物质释放），c表示浓度。

一般情况下，形式如上的对流扩散方程是无法求解的，因其难以确定恰当的初始条件。

在这种情况下，研究者们提出了不同的解析解算法，其目的是通过特定的分析步骤来求解该方程。

为此，研究者们将对流扩散方程分解成多个子方程，以便更容易的进行解析解析。

其中有许多不同的解析方法，这些方法大多建立在以下基础之上：1.量分离：将变量从原始方程分离出来，然后重新组合，使方程具有更好的求解性。

2.分替换：通过将复杂的积分变换成容易求解的形式，从而更容易求解对流扩散方程。

3.征方程：由于对流扩散方程的变量分离及积分替换，可以将其转换为简单的特征方程，从而可以更快地求出解析解。

4.值方法：这种方法采用计算机进行数值计算，可以从多个精度接近系统中求出解析解。

上述方法都可以用来求出对流扩散方程的解析解，但也存在一些潜在的问题，如数值误差、边界条件不易计算等。

对流扩散方程的解析解技术可以用来分析流体流动特性，模拟和分析气体湍流流动、热力学和传热运算等问题。

有了这些技术，研究者们可以更好地模拟或理解物理系统的流体特性，从而更好地解决实际中存在的问题。

例如，研究者可以利用对流扩散方程的解析解算法来分析汽车的空气动力学运动特性，有效改善汽车的燃油经济性和可靠性；或者用来研究空气流动的特性、助力涡轮机的性能改善；或者用来研究飞行器在进入大气时的热阻力特性，提高航天设备的安全性，等等。

对流扩散方程
1 流体扩散方程
流体扩散方程是一个历史悠久、解决常见力学概念的重要方法和
工具，它可以定量衡量复杂流体在双向运动和定向变化中经历的变化。

因此，它被广泛应用于流体动力学，比如在水动力和海洋动力学中。

2 原理
流体扩散方程基于小块体强迫传播的假定，从力学上讲，它是一
种可以解释流体物质的收支问题的方程。

由于流体受到外部力的影响，对某一点的流体运动行为可以用某种单元强迫块的形式进行观察，而
该点的微量物质的多元流变形式可以通过该块的公式来表示。

3 表达式
流体扩散方程的表达式如下：
$$\frac{\partial f}{\partial t}+ \vec{u} \cdot \nabla f = D \nabla^{2} f$$
其中：
$f$是流体属性函数；$\vec{u}$是流体速度；t是时刻；
$\nabla$和$\nabla{2}$是偏导数和二阶导数全称；D表示流体扩散率。

4 应用
流体扩散方程的应用广泛，可以解决流体运动与转移复杂问题。

比如在海洋科学中，它可以用来研究海洋的水文特征；在水力学中，
可以用来模拟水位和洪水洪峰等问题；在大气学领域，可以用来描述
大气给热扩散等问题；在机械工程中，可以模拟非稳定流、结构层HTML等问题。

5 结论
流体扩散方程是一种研究流体运动和转移问题的重要工具，它可
以分析流体行为，以便为设计解决复杂的流体问题提供有价值的答案。

此外，流体扩散方程也被应用于一些现实问题，例如气象学和机械工
程中的装配问题。

对流扩散方程及其解法对流扩散方程是物理学中最常见的一类偏微分方程，与流体力学、传热传质学等学科密切相关。

解析求解对流扩散方程可以揭示物理现象的本质，并在实际应用中提供有效的工程计算方法。

一、对流扩散方程对流扩散方程是将扩散项和对流项结合在一起的偏微分方程，一般形式如下：$$\dfrac{\partial u}{\partial t} = D\dfrac{\partial^2 u}{\partial x^2} - v\dfrac{\partial u}{\partial x} + f(x,t)$$其中 $u$ 是未知函数，$D$ 是扩散系数，$v$ 是速度场，$f(x,t)$ 是源项。

对流扩散方程描述了时间 $t$ 和空间 $x$ 上的某一物理量 $u$ 随时间的变化规律。

二、对流项与扩散项对流扩散方程中的对流项和扩散项代表不同的物理过程，互相作用形成物理现象。

对流项描述了物质由一点向另一点的移动，通常由质量流或者粒子流的线性变化来表示。

扩散项描述了物质的热或质量分布率随空间位置的二次变化。

对流项和扩散项的比值通常称为对流性能。

三、有限差分方法有限差分法是对流扩散方程的求解方法之一，将空间和时间的连续域离散化成离散点，并通过有限差分逼近偏微分方程的微分项，从而转化成一个代数问题。

常见的有限差分格式有向后差分法、向前差分法、中心差分法等。

假设在 $(x_i,t_n)$ 的数值解已知，设网格步长为 $\Delta x$ 和$\Delta t$，则有：$$u(x_i,t_{n+1}) \approx u(x_i,t_{n}) + \Delta tf(u(x_i,t_n),x_i,t_n)$$其中 $f(u(x_i,t_n),x_i,t_n)$ 是对流扩散方程右端的非线性项。

将$u(x_i,t_n)$ 用它四周的$u(x_{i-1},t_n)$、$u(x_{i+1},t_n)$、$u(x_i,t_{n-1})$ 替代，可以得到向后差分格式：$$u(x_i,t_{n+1}) \approx u(x_i,t_{n}) + D\dfrac{\Delta t}{\Deltax^2}[u(x_{i+1},t_n) - 2u(x_i,t_n) + u(x_{i-1},t_n)]-v\dfrac{\Deltat}{\Delta x}[u(x_{i+1},t_n) - u(x_{i-1},t_n)] + \Delta tf(u(x_i,t_n),x_i,t_n)$$四、求解方法对流扩散方程的解法包括解析解和数值解，主要取决于方程的形式和边界条件的选取。