道路平曲线超高加宽计算

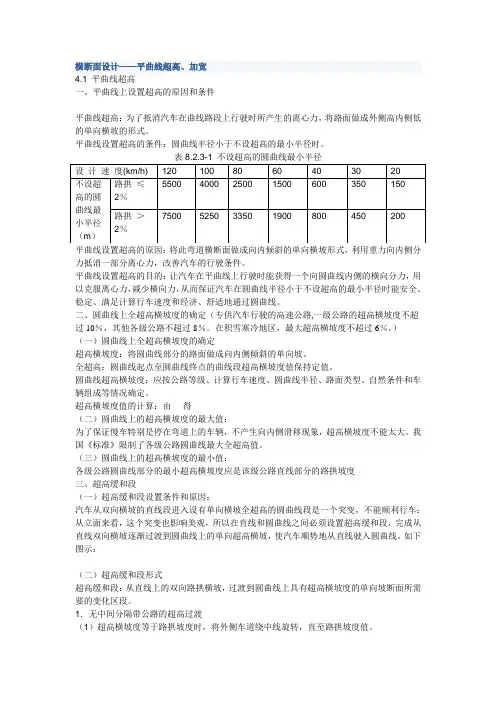
（2）超高横坡度大于路拱坡度时，可分别采用以下三种方式：图2—12 无中间分隔带公路的超高过渡绕内边缘线旋转先将外侧车道绕路面未加宽前的中心线旋转，待达到与内侧车道构成单向横坡后，整个断面绕路面未加宽前的内侧边缘线旋转，直至全超高横坡度值。

绕中线旋转先将外侧车道绕路面未加宽前的路中心线旋转，待达到与内侧构成单向横坡后，整个断面一同绕路面未加宽前的路中心线旋转，直至全超高横坡度值。

绕外边缘线旋转先将外侧车道绕路面外侧边缘旋转，与此同时，内侧车道随中线的降低而相应降低，待达到单向横坡后，整个断面仍绕外侧车道边缘旋转，直至超高横坡值。

一般新建公路多用绕内边缘线旋转方式；旧路改建工程多用绕中心线旋转方式；绕外侧边缘线旋转是一种比较特殊的设计，仅用于某些为改善路容的地点。

2．有中间分隔带公路的超高过渡（1）绕中央分隔带的中心线旋转先将外侧行车道绕中央分隔带的中心线旋转，待达到与内侧行车道构成单向横坡后，整个断面一同绕中央分隔带的中心线旋转，直至全超高横坡值。

（2）绕中央分隔带两侧边缘线旋转将两侧行车道分别绕中央分隔带两侧边缘线旋转，使之各自成为独立的单向超高断面。

此时中央分隔带维持原水平状态。

（3）绕各自行车道中线旋转将两侧行车道分别绕各自的行车道中心线旋转，使之各自成为独立的单向超高断面，此时中央分隔带两边缘分别升高与降低而成为倾斜断面。

三种超高过渡方式各有优缺点，中间带宽度较窄时可采用绕中央分隔带的中心线旋转；各种中间带宽度的都可以采用绕中央分隔带的两侧边缘旋转；对于车道数大于4条的公路可采用绕各自行车道中心线旋转；图2—13 有中间分隔带公路的超高过渡（三）超高缓和段长度为了行车的舒适、路容的美观和排水的通畅，必须设置一定长度的超高缓和段，超高的过渡则是在超高缓和段全长范围内进行的。

双车道公路超高缓和段长度按下式计算：（2—23）式中：Lc —超高缓和段长度； B —旋转轴至行车道外侧边缘的宽度（m）；△i —超高旋转轴外侧的最大超高横坡度与原路拱横坡度的代数差；p —超高渐变率（由于逐渐超高而引起外侧边缘纵坡与路线原设计纵坡的差值）。

第6 卷第3 期2 0 0 4 年9 月辽宁省交通高等专科学校学报J OU RNAL OF L IAON IN G PROV INCIAL COLL EGE OF COMMUN ICA TIONSVol. 6 No . 3Sep . 2 0 0 4文章编号:1008 - 3812 (2004) 03 - 0030 - 03高速公路超高与加宽设计计算方法王功礼1 姚丽2 翁振军1(1. 辽宁省高速公路管理局,辽宁沈阳,110003 ;2. 辽宁省交通高等专科学校,辽宁沈阳,110122)摘要本文通过以两车道为主的高速公路超高和加宽的设计方法的实践,建立了一种简便的超高与加宽的计算模型,并介绍其计算方法。

关键词高速公路超高加宽计算方法中图分类号:U412 文献标识码:B1 前言表 1在现代公路设计中,不同等级公路的超高和加宽设计计地形计算行车速度( km/ h) 不设超高最小半径( m)算方法不尽相同,虽然基本原理比较相似,但计算方法复杂、繁琐。

近几年来,我们在辽宁省丹本高速公路( 山区高速公路) 的施工和管理过程中,仔细分析了设计方案及施工工艺, 总结一套简易而实用的超高和加宽设计方案。

此方案更适用一般平原高速公路(四车道) 及一至四级普通公路建设。

平原微丘重丘山岭2. 2 超高的形成120100806055004000250015002 超高设计2. 1 超高的作用及设计条件2. 1. 1 超高的作用超高是将公路曲线部分的路面设计成向曲线内侧倾斜的单向横坡,使得汽车在曲线上行驶时能够获取一个指向曲线内侧的横向分力,以克服或削弱离心力对行车的影响。

2. 1. 2 超高设置条件《公路工程技术标准》规定,当平曲线半径小于不设超高的半径时,应在曲线上设置超高。

其超高横坡度可由下式求得:i b = V2/ 127R - μV —行车速度R —平曲线半径μ—横向力系数不设超高的圆曲线最小半径见表 1 。

收稿日期:2004 - 04 - 10同迎来一个更加辉煌的前景。

超高过渡介绍公路超高过渡一、低等级公路超高计算【示例1】山岭重丘区某新建二级公路，设计速度为40km/h，其中一平曲线半径R＝150m，缓和曲线Ls＝70m，路面宽度为B＝7.0m，路肩宽度为0.75m，路拱坡度为iG＝2%，路肩坡度iJ＝3%，该曲线的主点桩号分别为：ZH＝K1+028.665 、HY＝K1+098.665 、QZ＝K1+131.659 、YH＝K1+164.653 、HZ＝K1+234.653。

试计算各主点桩以及下列桩号：K1+040、K1+070、K1+180、K1+210处横断面上内外侧和路中线三点的超高值（设计高为路基边缘）。

（1）确定超高缓和段长度根据公路等级、设计速度和平曲线半径查表得圆曲线的超高值iy＝5％，新建公路一般采用绕边线旋转，超高渐变率p＝1/100，所以超高缓和段长度：Lc＝B'△i/p＝7×5%/(1/100)=35.0(m)而缓和曲线Ls＝70m，先取Lc＝Ls＝70m，然后检查横坡从路拱坡度（－2%）过渡到超高横坡（2%）时的超高渐变率：p=3.5×[2%-(-2%)]/X0=3.5×[2%-(-2%)]/28=1/200>1/330或p=7×5%/70=1/200>1/330所以取Lc＝Ls＝70m。

（2）计算临界断面x0X0＝iG/ih×Lc＝2%/5%×70＝28.0m（3）计算各桩号处的超高值超高起点为ZH（HZ）点，分别计算出x值，然后分别代入超高值计算公式（见《道路勘测设计》书）中计算，加宽过渡采用比例过渡，加宽值b＝1.0m。

土路肩在超高起点前1m变成与路面相同的横坡，且在整个超高过过渡段保持与相邻行车道相同的横坡。

计算结果见下表。

超高值计算结果表桩号 x 加宽值bx 外侧超高值中线超高值内侧超高值K1+028.665（ZH） 0.000<x0＝28 0.000 0.008 0.093 0.008+040 11.335< x0＝28 0.162 0.073 0.093 0.004+070 41.335 >x0＝28 0.591 0.245 0.126 -0.017+098.665（HY） 1.000 0.410 0.198 -0.065+131.659（QZ） 1.000 0.410 0.198 -0.0651+164.653（YH） 1.000 0.410 0.198 -0.065+180 54.653> x0＝28 0.781 0.322 0.159 -0.037+210 24.653< x0＝28 0.352 0.149 0.093 0.000+234.653（HZ） 0.000< x0＝28 0.000 0.008 0.093 0.008（已知第一段坡度i1,第二段坡度i2,过度段长度l,待求点离第二横坡距离xa=x/l待求点i=(i2-i1)(1-3a2+2a3)+i1）二．超高缓和段长度计算超高缓和段的长度按下式计算：Lc＝B'×△i/P式中： Lc——超高缓和段长度(m);B' ——旋转轴至行车道（设路缘带时为路缘带）外侧边缘的宽度（m）；△i——旋转轴外侧的超高与路拱坡度的代数差；P ——超高渐变率，其值根据计算行车速度和超高过渡方式从下表中查取。

公路超高过渡一、低等级公路超高计算【示例1】山岭重丘区某新建二级公路，设计速度为40km/h，其中一平曲线半径R＝150m，缓和曲线Ls＝70m，路面宽度为B＝7.0m，路肩宽度为0.75m，路拱坡度为iG＝2%，路肩坡度iJ＝3%，该曲线的主点桩号分别为：ZH＝K1+028.665 、HY＝K1+098.665 、QZ＝K1+131.659 、YH＝K1+164.653 、HZ＝K1+234.653。

试计算各主点桩以及下列桩号：K1+040、K1+070、K1+180、K1+210处横断面上内外侧和路中线三点的超高值（设计高为路基边缘）。

（1）确定超高缓和段长度根据公路等级、设计速度和平曲线半径查表得圆曲线的超高值iy＝5％，新建公路一般采用绕边线旋转，超高渐变率p＝1/100，所以超高缓和段长度：Lc＝B'△i/p＝7×5%/(1/100)=35.0(m)而缓和曲线Ls＝70m，先取Lc＝Ls＝70m，然后检查横坡从路拱坡度（－2%）过渡到超高横坡（2%）时的超高渐变率：p=3.5×[2%-(-2%)]/X0=3.5×[2%-(-2%)]/28=1/200>1/330或p=7×5%/70=1/200>1/330所以取Lc＝Ls＝70m。

（2）计算临界断面x0X0＝iG/ih×Lc＝2%/5%×70＝28.0m（3）计算各桩号处的超高值超高起点为ZH（HZ）点，分别计算出x值，然后分别代入超高值计算公式（见《道路勘测设计》书）中计算，加宽过渡采用比例过渡，加宽值b＝1.0m。

土路肩在超高起点前1m变成与路面相同的横坡，且在整个超高过过渡段保持与相邻行车道相同的横坡。

计算结果见下表。

超高值计算结果表桩号x 加宽值bx 外侧超高值中线超高值内侧超高值K1+028.665（ZH）0.000<x0＝28 0.000 0.008 0.093 0.008+040 11.335< x0＝28 0.162 0.073 0.093 0.004+070 41.335 >x0＝28 0.591 0.245 0.126 -0.017+098.665（HY） 1.000 0.410 0.198 -0.065+131.659（QZ） 1.000 0.410 0.198 -0.0651+164.653（YH） 1.000 0.410 0.198 -0.065+180 54.653> x0＝28 0.781 0.322 0.159 -0.037+210 24.653< x0＝28 0.352 0.149 0.093 0.000+234.653（HZ）0.000< x0＝28 0.000 0.008 0.093 0.008（已知第一段坡度i1,第二段坡度i2,过度段长度l,待求点离第二横坡距离xa=x/l待求点i=(i2-i1)(1-3a2+2a3)+i1）二．超高缓和段长度计算超高缓和段的长度按下式计算：Lc＝B'×△i/P式中：Lc——超高缓和段长度(m);B' ——旋转轴至行车道（设路缘带时为路缘带）外侧边缘的宽度（m）；△i——旋转轴外侧的超高与路拱坡度的代数差；P ——超高渐变率，其值根据计算行车速度和超高过渡方式从下表中查取。

第三节缓和段一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间，由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。

1．缓和曲线的作用1）便于驾驶员操纵方向盘2）乘客的舒适与稳定，减小离心力变化3）满足超高、加宽缓和段的过渡，利于平稳行车4）与圆曲线配合得当，增加线形美观2．缓和曲线的性质为简便可作两个假定：一是汽车作匀速行驶；二是驾驶员操作方向盘作匀角速转动，即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。

S=A2/ρ（A：与汽车有关的参数）ρ=C/s C=A2由上式可以看出，汽车行驶轨迹半径随其行驶距离递减，即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比，此方程即回旋线方程。

3．回旋线基本方程即用回旋线作为缓和曲线的数学模型。

令：ρ=R，lh=s 则 lh=A2/R4．缓和曲线最小长度缓和曲线越长，其缓和效果就越好；但太长的缓和曲线也是没有必要的，因此这会给测设和施工带来不便。

缓和曲线的最小长度应按发挥其作用的要求来确定：1）根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性，就需控制离心力的变化率。

a1=0,a2=v2/ρ,as=Δa/t≤0.62）依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3）根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡（即超高渐变率）是指在缓和曲线上设置超高缓和段后，因路基外侧由双向横坡逐渐变成单向超高横坡，所产生的附加纵坡。

4）从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间，视觉效果好。

《公路工程技术标准》规定：按行车速度来求缓和曲线最小长度，同时考虑行车时间和附加纵坡的要求。

5．直角坐标及要素计算1）回旋线切线角（1）缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。

βx=s2/2Rlh（2）缓和曲线的总切线角β=lh/2R.180/л2）缓和曲线直角坐标任意一点P处取一微分弧段ds，其所对应的中心角为dβxdx=dscosβxdy=dssinβx3）缓和曲线常数（1）主曲线的内移值p及切线增长值q内移值：p=Yh-R(1-cosβh)=lh2/24R切线增长值：q=Xh-Rsinβh=lh/2-lh3/240R2（2）缓和曲线的总偏角及总弦长总偏角：βh=lh/2R总弦长：Ch=lh-lh3/90R2O为圆曲线的圆心，圆曲线所对圆心角（等于公路偏角）。