七年级数学上册动角问题专项练习(20200707221904)
- 格式:pdf
- 大小:855.42 KB
- 文档页数:4
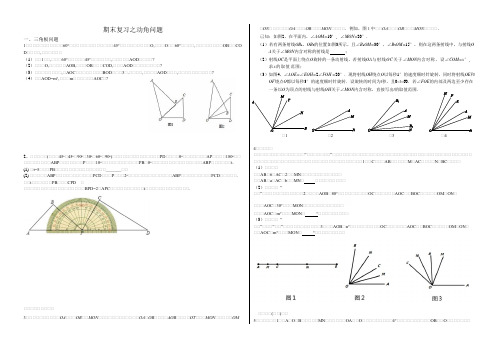
期末复习之动角问题一、三角板问题1、、、、、、、、、、、60°、、、、、、、、、、、、、45°、、、、、、、、、O,、、、O、、60°、、、、,、、、、、、、、OB、、COD、、、、,、、、、、、(1)、、1、、,、、、60°、、、、、45°、、、、、、,、、、、、AOD、、、、?(2)、、、O,、、、、、AOB,、、、OB、、、COD,、、、AOD、、、、、、、、?(3)、、、、、、、、,、AOC、、、、、、、、BOD、、、3、.、、、、,、、、、AOD、、、,、、、、、、、、、、?(4)、、AOD=m°,、、、m、、、、、、AOC、?2、、、、、、(、、、45o、45o、90o、30o、60o、90o)、、、、、、、、、、、、、、PD、、、、0o、、、、、、、AP、、、、180o、、、、、、、、、、ABP、、、、、、、P、、、10o、、、、、、、、、、、PB、0o、、、、、、、、、、、、、、、ABP、、、、、、t.(1)、t=5、、、PB、、、、、、、、、、、、、、、_______、、(2)、、、、、ABP、、、、、、、、、、、PCD、、、P、、、2o、、、、、、、、、、、、、ABP、、、、、、、、、PCD、、、、、.、、t、、、、、、PB、、、CPD、、、、、、、、、、、、、、、、、、、BPD=2、APC、、、、、、、、、、t、、、、、、、、、、、、、.、、、、、、、、、3、、、、、、、、、、OA、、、OB、、MON、、、、、、、、、、、、OA、OB、、、、AOB、、、、OT、、、MON、、、、、OM、ON、、、、、、OA、、、OB、、、MON、、、、.例如,图1中、、OA、、、OB、、、MON、、、、.已知:如图2,在平面内,∠AOM=10°, ∠MON=20°.(1)若有两条射线OB1,OB2的位置如图3所示,且∠B1OM=30°,∠B2OM=15°,则在这两条射线中,与射线O A关于∠MON内含对称的射线是;(2)射线OC是平面上绕点O旋转的一条动射线,若射线OA与射线OC关于∠MON内含对称,设∠COM=x°,求x的取值范围;(3)如图4,∠AOE=∠EOH=2∠FOH =20°.现将射线OH绕点O以每秒1°的速度顺时针旋转,同时将射线OE和OF绕点O都以每秒3°的速度顺时针旋转.设旋转的时间为t秒,且0<t<60.若∠FOE的内部及两边至少存在一条以O为顶点的射线与射线OH关于∠MON内含对称,直接写出t的取值范围.4、、、、、、、、、、、、、、、、、、、、“、、、、、、、”、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、1、、C、、、AB、、、、、M、AC、、、、N、BC、、、、(1)、、、、、、AB、6、AC、2、、MN、、、、、、、、、、、、、、AB、a、AC、b、、MN、、、、、、、、、、(2)、、、、“、、”、、、、、、、、、、、、2、、、、AOB、80°、、、、、、、、、OC、、、、、、AOC、、BOC、、、、、OM、ON、、、、AOC、30°、、、MON、、、、、、、、、、、、、、、AOC、m°、、、MON、°、、、、、、、、、(3)、、、、“、、”、、、“、、”、、、、、、、、、、、3、、、AOB、n°、、、、、、、、、OC、、、、、、AOC、、BOC、、、、、OM、ON、、、AOC、m°、、、MON、°、、、、、、、、、、、、、(、、)、、5、、、、、、1、、A、O、B、、、、、MN、、、、、、OA、、O、、、、、、、、、4°、、、、、、、、、、OB、、O、、、、、、、、1 、2 、3、4、、6°、、、、、、、、MN、、、、、、、2、、、、、、、t、0、≤t≤60、、、 、1、、、t、、、、、、、MOA、、、、、2、、、、、、、、、、AOB、、、、、72°、、、t、、、、3、、、、、、、、、、、、、、t、、、、、OB、、、OA、、、、、、、、、、、、、t、、、、、、、、、、、、、、、6、如图(1),O 为直线AB 上点,过点O 作射线OC ,、AOC=30°,将一直角三角尺(、M=30°)的直角顶点放在点O 处,一边ON 在射线OA 上,另一边OM 与OC 都在直线AB 的上方.(1)若将图(1)中的三角尺绕点O 以每秒5o 的速度,沿顺时针方向旋转t 秒,当OM 恰好平分、BOC 时, 如图(2)①求t 值; ②试说明此时ON 平分、AOC ;(2)将图(1)中的三角尺绕点O 顺时针旋转,设AON α∠=,COM β∠=, 当ON 在、AOC 内部时,试求α与β的数量关系;(3)若将图(1)中的三角尺绕点O 以每秒5︒的速度沿顺时针方向旋转的同时,射线OC 也绕点O 以每秒8︒的速度沿顺时针方向旋转,如图(3),那么经过多长时间,射线OC 第一次平分MON ∠?请说明理由.四、、、、、、、7、、、1、B、、、AD、、、、、、A→D→A、、、、2cm/s、、、、、、、1、、C、、、BD、、、、AD=10cm、、、B、、、、、t、、0≤t≤10、、、1、、t=2、、、AB= ___ cm、、、、CD= cm 、2、、、t、、、、、、、、、、、AB、、、、3、、、、、、、、、AB、、、E、、EC、、、、、、、、、B、、、、、、、、、4、、、、、、、、、、、AOD=120°、OC、OD、、、O、、、、、、OE、OC、、、、、AOB、、BOD 、、BOC、、、、、、、、、、、OB、、、、、、、、8、、、、AOB、80°、OC、、、O、、、、、、OD、OE、、、、、AOC、、BOC、、、、、、、、、 、1、、、、、、、OC、、AOB、、、、、、、DOE、、、、、、、(2)、、、、、、OC、、AOB、、、、、、、、、、、DOE、、、、、、、、、、、、(3)、、、、、、OC、、AOB、、、、、、、、、、、DOE、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、9、、、1、、、、、、、、、、、、、、、、、、、0、、、、、、、、、、、C、、、、、、、、、、OA、、 、、、ABO=、DCO=90°、AOB=45°、C=60°,、、AO D 、、、、、、CD、、E (1) 、、BO E、、、、(2) 、、2、、、C、、、、OA、、、、COE=15°、、 、、BOD、、、、。


专题4.6 动角问题专项训练(40道)【人教版】考卷信息:本套训练卷共40题,题型针对性较高,覆盖面广,选题有深度,涵盖了动角的综合问题的所有类型!一.解答题(共40小题)1.(2022·吉林白山·七年级期末)如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,|∠1﹣∠2|=90°,则∠1和∠2互为垂角.(本题中所有角都是指大于0°且小于180°的角)(1)如图1所示,O为直线AB上一点,∠AOC=90°,则∠AOD垂角为和;,求这个角的度数;(2)如果一个角的垂角等于这个角的补角的23(3)如图2所示,O为直线AB上一点,∠AOC=90°,∠BOD=30°,且射线OC绕点O以9°/s 的速度逆时针旋转,射线OD绕点O以6°/s的速度顺时针旋转,两条射线OC、OD同时运动,运动时间为t s(0<t<20),试求当t为何值时,∠AOC和∠AOD互为垂角.2.(2022·四川成都·七年级期末)如图1,点D、O、A共线且∠COD=20°,∠BOC=80°,射线OM,ON分别平分∠AOB和∠BOD.如图2,将射线OD以每秒6°的速度绕点O顺时针旋转一周,同时将∠BOC以每秒4°的速度绕点O顺时针旋转,当射线OC与射线OA重合时,∠BOC停止运动.设射线OD的运动时间为t.(1)运动开始前,如图1,∠AOM=°,∠DON=°;(2)旋转过程中,当t为何值时,射线OB平分∠AON?(3)旋转过程中,是否存在某一时刻使得∠MON=35°?若存在,请求出t的值;若不存在,请说明理由.3.(2022·重庆·西南大学附中七年级期中)如图①,已知∠AOB,在∠AOB内部画射线OC,得到三个角,分别为∠AOC、∠BOC、∠AOB.若这三个角中有一个角是另外一个角的3倍,则称射线OC为∠AOB的“幸福线”.(本题中所研究的角都是大于0°而小于180°的角.)(1)角的三等分线________这个角的“幸福线”(填“是”或“不是”);(2)如图①,∠AOB=45°,射线OC为∠AOB的“幸福线”,求∠AOC的度数;(3)如图②,已知∠AOB=60°,射线OM从OA出发,以每秒20°的速度绕O点逆时针旋转,同时,射线ON从OB出发,以每秒15°的速度绕O点逆时针旋转,设运动的时间为t秒(0<t< 9).若OM、ON、OA三条射线中,一条射线恰好是以另外两条射线为边的角的“幸福线”,求出所有可能的t值.4.(2022·四川成都·七年级期末)【阅读理解】定义:在一条直线同侧的三条具有公共端点的射线之间若满足以下关系,其中一条射线分别与另外两条射线组成的角恰好满足2倍的数量关系,则称该射线是另外两条射线的“双倍和谐线”.如图1,点P在直线l上,射线PR,PS,PT位于直线l同侧,若PS平分∠RPT,则有∠RPT=2∠RPS,所以我们称射线PR是射线PS,PT的“双倍和谐线”.【迁移运用】(1)如图1,射线PS(选填“是”或“不是”)射线PR,PT的“双倍和谐线”;射线PT(选填“是”或“不是”)射线PS,PR的“双倍和谐线”;(2)如图2,点O在直线MN上,OA⊥MN,∠AOB=40°,射线OC从ON出发,绕点O以每秒4°的速度逆时针旋转,运动时间为t秒,当射线OC与射线OA重合时,运动停止.①当射线OA是射线OB,OC的“双倍和谐线”时,求t的值;②若在射线OC旋转的同时,∠AOB绕点O以每秒2°的速度逆时针旋转,且在旋转过程中,射线OD平分∠AOB.当射线OC位于射线OD左侧且射线OC是射线OM,OD的“双倍和谐线”时,求∠CON的度数.5.(2022·浙江金华·七年级期末)阅读理解:在钟面上,把一周分成12个大格,每个大格分成5个小格,所以每个大格对应的是30°角,每个小格对应的是6°角,时针每分钟转过的角度是0.5度,分针每分针转过的角度是6度.(1)解决问题:当时钟的时刻是8:30时,求此时分针与时针所夹的锐角的度数.(2)8:00开始几分钟后分针第一次追上时针.(3)设在8:00时,分针的位置为OA,时针的位置为OB,运动后的分针为OP,时针为OQ.问:在8:00~9:00之间,从8:00开始运动几分钟,OB,OP,OQ这三条射线,其中一条射线是另外两条射线所夹的角的平分线?6.(2022·贵州铜仁·七年级期末)沿河县某初中七年级的数学老师在课外活动中组织学生进行实践探究,用一副三角尺(分别含45°,45°,90°和30°,60°,90°的角)按如图所示摆放在量角器上,边PD与量角器180°刻度线重合,边AP与量角器0°刻度线重合,将三角尺ABP 绕量角器中心点P以每秒10°的速度顺时针旋转,当边PB与180°刻度线重合时停止运动,设三角尺ABP的运动时间为t秒.(1)当t=5时,∠BPD=__________°;(2)若在三角尺ABP开始旋转的同时,三角尺PCD也绕点P以每秒2°的速度逆时针旋转,当三角尺ABP停止旋转时,三角尺PCD也停止旋转.①当t为何值时,边PB平分∠CPD;②在旋转过程中,是否存在某一时刻使∠BPD=2∠APC,若存在,请求出t的值;若不存在,请说明理由.7.(2022·浙江宁波·七年级期末)如图1, 已知∠AOB=120°,射线OP从OA位置出发,以每秒2°的速度按顺时针方向向射线OB旋转;与此同时,射线OQ以每秒4°的速度,从OB位置出发按逆时针方向向射线OA旋转,到达射线OA后又以同样的速度按顺时针方向返回,当射线OP与射线OB重合时,两条射线同时停止运动,设旋转时间为t(s).(1)当t=5时,求∠POQ的度数;(2)当OP与OQ重合时,求t的值;(3)如图2,在旋转过程中,若射线OC始终平分∠AOQ,问:是否存在t的值,使得∠POQ=∠COQ?若存在,请直接写出t的值;若不存在,请说明理由.8.(2022·福建·厦门市逸夫中学七年级期末)如图,两条直线AB,CD相交于点O,且∠AOC=90°,射线OM从OB开始绕O点逆时针方向旋转,速度为15°/s,射线ON同时从OD 开始绕O点顺时针方向旋转,速度为12°/s.两条射线OM,ON同时运动,运动时间为t秒.(本题出现的角均小于平角)(1)当t=2时,∠MON=_______,∠AON=_______;(2)当0<t<12时,若∠AOM=3∠AON=60°.试求出t的值;的值,问:t满足怎样的条件是定值;满足怎样的条(3)当0<t<6时,探究∠BON−∠COM+∠AOC∠MON件不是定值?9.(2022·福建·泉州七中七年级期末)如图1,O为直线AB上一点,过点O作射线OC,∠AOC =30°,将一直角三角尺(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.(1)若将图1中的三角尺绕点O以每秒5°的速度,沿顺时针方向旋转t秒,当OM恰好平分∠BOC时,如图2.①求t值;②试说明此时ON平分∠AOC;(2)将图1中的三角尺绕点O顺时针旋转,设∠AON=α,∠COM=β,当ON在∠AOC内部时,试求α与β的数量关系;(3)如图3若∠AOC=60°,将三角尺从图1的位置开始绕点O以每秒5°的速度沿顺时针方向旋转.当ON与OC重合时,射线OC开始绕点O以每秒20°的速度沿顺时针方向旋转,三角尺按原来的速度和方向继续旋转,当三角板运动到OM边与OA第一次重合时停止运动.当射线OC运动到与OA第一次重合时停止运动.设三角形运动的时间为t.那么在旋转的过程中,是否存在某个时刻,使得ON,OM两条边所在的射线及射线OC,三条射线中的某一条射线是另两条射线的角平分线?若存在,直接写出所有满足条件的t的值,若不存在,请说明理由.10.(2022·江苏盐城·七年级期末)【阅读理解】∠BOC,则称射线OC是射线OA在∠AOB内射线OC是∠AOB内部的一条射线,若∠COA=12∠BOC,所以射线OC是射的一条“友好线”.如图1,∠AOB=60°,∠AOC=20°,则∠AOC=12线OA在∠AOB内的一条“友好线”.【解决问题】(1)在图1中,若作∠BOC的平分线OD,则射线OD射线OB在∠AOB内的一条“友好线”;(填“是”或“不是”)(2)如图2,∠AOB的度数为n,射线OM是射线OB在∠AOB内的一条“友好线”,ON平分∠AOB,则∠MON的度数为;(用含n的代数式表示)(3)如图3,射线OB从与射线OA重合的位置出发,绕点O以每秒3°的速度逆时针旋转;同时,射线OC从与射线OA的反向延长线重合的位置出发,绕点O以每秒5°的速度顺时针旋转,当射线OC与射线OA重合时,运动停止.问:当运动时间为多少秒时,射线OA、OB、OC中恰好有一条射线是余下两条射线中某条射线在余下两条射线所组成的角内的一条“友好线”?11.(2022·湖北武汉·七年级期末)定义:过角的顶点在角的内部作一条射线,得到三个角,若这三个角中有一个角是另外一个角的两倍,则称这条射线为这个角的“二倍角线”.(1)如图1,∠AOB=120°,射线OC为∠AOB的“二倍角线”,则∠AOC=.(2)如图2,射线OB为∠COD的“二倍角线”,且∠DOB=2∠BO C.射线OM、ON分别为∠AOC、的值是否为定值?若是,求出其值;若不是,请说明理由;∠BOD的平分线,问∠AOD+∠BOC∠MON(3)如图3.已知∠AOB=120°,射线OC、OD为∠AOB的“二倍角线”,且∠COB=2∠AO C.∠AOD =2∠BOD,将∠COD绕点O以10°/秒的速度顺时针转动,运动时间为t秒(0≤t≤14),射线OM、ON分别为∠AOC、∠BOD的平分线.OB、OM、ON三条射线中,一条射线恰好是以另外两条射线为边组成的角的“二倍角线”,直接写出t所有可能的值.12.(2022·天津南开·七年级期末)已知:如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=1:5.将一等腰直角三角板的直角顶点放在点O处,一直角边ON 在射线OB上,另一直角边OM在直线AB的下方.(1)将图1中的等腰直角三角板绕点O以每秒3°的速度逆时针方向旋转一周,直角边ON旋转后的对应边为ON',直角边OM旋转后的对应边为OM'.在此过程中,经过t秒后,OM'恰好平分∠BOC,求t的值;(2)如图2,在(1)问的条件下,若等腰直角三角板在转动的同时,射线OC也绕点O以每秒4°的速度顺时针方向旋转,射线OC旋转后的对应射线为OC'.当射线OC'落在射线OC的反向延长线上时,射线OC和等腰直角三角板同时停止运动.在此过程中,是否存在某一时刻t,使得OC'//M'N'.若存在,请求出t的值,若不存在,诮说明理由;(3)如图3,在(1)问的条件下,若等腰直角三角板在转动的同时,射线OC也绕点O以每秒5°的速度顺针方向旋转,射线OC旋转后的对应射线为OC'.当等腰直角三角板停止运动时,射线OC也停止运动.在整个运动过程中.经过l秒后,∠M'ON'的某一边恰好平分∠AOC',请直接写出所有满足条件的t的值.13.(2022·山西晋中·七年级期末)综合与探究:射线OC是∠AOB内部的一条射线,若∠COA= 1∠BOC,则我们称射线OC是射线OA的伴随线.例如,如图1,∠AOB=60°,∠AOC=∠COD= 2∠BOD=20°,则∠AOC=1∠BOC,称射线OC是射线OA的伴随线;同时,由于∠BOD=21∠AOD,称射线OD是射线OB的伴随线.2完成下列任务:(1)如图2,∠AOB=150°,射线OM是射线OA的伴随线,则∠AOM=°,若∠AOB的度数是x,射线ON是射线OB的伴随线,射线OC是∠AOB的平分线,则∠NOC的度数是.(用含x 的代数式表示)(2)如图3,如∠AOB=180°,射线OC与射线OA重合,并绕点O以每秒6°的速度逆时针旋转,射线OD与射线OB重合,并绕点O以每秒10°的速度顺时针旋转,当射线OD与射线OA重合时,运动停止.①是否存在某个时刻t(秒),使得∠COD的度数是20°,若存在,求出t的值,若不存在,请说明理由;②当t为多少秒时,射线OC,OD,OA中恰好有一条射线是其余两条射线的伴随线.请直接写出结果.14.(2022·陕西·西安高新一中实验中学七年级期末)如图所示,OA,OB,OC是以直线EF上一点O为端点的三条射线,且∠FOA=20°,∠AOB=60°,∠BOC=10°,射线OP从OF处开始出发,绕点O逆时针匀速旋转,旋转速度为每秒5度:射线OQ从OC处开始出发,绕点O顺时针匀速旋转,两条射线同时开始旋转(当射线OQ旋转至与射线OF重合时,OP、OQ同时停止运动),旋转时间为t秒.(旋转速度÷旋转角度:旋转时间)(1)当t=秒,射线OP平分∠AOB时;(2)若射线OQ的旋转速度为每秒4度时,请求出当∠POQ=60°时,射线OP旋转的时间;(3)若射线OQ的旋转速度为每秒3度时,是否存在某个时刻,使得射线OQ,OP,OB中的某一条射线是另两条射线所夹角的角平分线?若存在,请直接写出所有满足题意的的值,若不存在,请说明理由.15.(2022·浙江杭州·七年级期中)在同一平面内的三条射线OA、OB、OC,①当射线OC在∠AOB内时,若满足∠AOC=2∠COB,则称射线OC是【OA,OB】的好线;若满足∠BOC=2∠AOC,则称射线OC是【OB,OA】的好线;②当射线OC在∠AOB外时,若满足∠AOC=2∠COB,称射线OC是【OA,OB】的皮线.(1)如图1,∠AOD=∠DOC=∠COB=20°,则射线OC是【OA,OB】的好线,又是【OA,OD】的皮线;射线______是【OB,OA】的好线,又是____的皮线.(2)如图2,点O在线段AB上,∠BOD=30°,∠AOC=60°,求【OC,OD】的好线与OA的夹角(写出完整的解答过程).(3)如图3,点O在直线AB上,∠BOD=30°, ∠AOC=60°,射线OM从OC位置出发以每秒10°的速度绕着点O逆时针方向旋转,设旋转时间为t(0<t<12))秒.①求当t为何值时,【OB,OM】的皮线与OC垂直?②若有射线ON从OD位置与射线OM同时出发以每秒5°的速度绕着点O顺时针方向旋转,并与射线OM同时停止运动,求当t为何值时,OM、OB、ON三条射线中恰好能使得其中一条为其余两条的好线(直接写出答案).16.(2022·广东汕头·七年级期末)已知∠AOB=150°,射线OP从OB出发,绕O逆时针以1°/秒的速度旋转,射线OQ从OA出发,绕O顺时针以3°/秒的速度旋转,两射线同时出发,运动时间为t秒(0<t≤60)(1)当t=12秒时,求∠POQ;(2)当OP⊥OQ,求t的值;(3)射线OP,OQ,OB,其中一条射线是其他两条射线所形成的角的平分线,求t的值.17.(2022·湖北武汉·七年级期末)问题背景整体思想就是从问题的整体性质出发,突出对问题的整体结构的分析,把握它们之间的关联,进行有目的、有意识的整体处理,整体思想在代数和几何中都有很广泛的应用.(1)如图1,A、B、O三点在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC,则∠DOE 的度数为(直接写出答案).(2)当x=1时,代数式a x3+bx+2021的值为2020,当x=﹣1时,求代数式a x3+bx+2021的值.(3)①如图2,点C是线段AB上一定点,点D从点A、点E从点B同时出发分别沿直线AB 向左、向右匀速运动,若点E的运动速度是点D运动速度的3倍,且整个运动过程中始终的值;满足CE=3CD,求ACAB②如图3,在①的条件下,若点E沿直线AB向左运动,其它条件均不变.在点D、E运动的过程中,点P、Q分别是AE、CE的中点,若运动到某一时刻,恰好CE=4PQ,求此时ADAB 值.18.(2022·四川·麓山师大一中七年级阶段练习)如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=3∠AOC,将一直角三角板的直角顶点放在点O处,边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O按逆时针方向旋转45°至图2的位置,则∠MOC=______°.(2)将图1中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部,试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由.(3)将图1中的三角尺绕着点O以每秒15°的速度按逆时针方向旋转;同时,射线OC也绕着点O以每秒5°的速度按逆时针方向旋转,当一方先完成旋转一周时停止,另一方同时也停止转动,当射线OC恰好平分∠MON时,求此时三角板绕点O的运动时间t的值.19.(2022·山东临沂·七年级期末)已知∠AOB=150°,OC为∠AOB内部的一条射线,∠BOC= 60°.∠BOD,求∠DOE的(1)如图1,若OE平分∠AOB,OD为∠BOC内部的一条射线,∠COD=12度数;(2)如图2,若射线OE绕着O点从OA开始以15度/秒的速度顺时针旋转至OB结束、OF 绕着O点从OB开始以5度/秒的速度逆时针旋转至OA结束,运动时间t秒,当∠EOC=∠FOC 时,求t的值.20.(2022·湖北武汉·七年级期末)如图1,平面内一定点A在直线EF的上方,点O为直线EF上一动点,作射线OA、OP、OA',当点O在直线EF上运动时,始终保持∠EOP=90°、∠AOP =∠A'OP,将射线OA绕点O顺时针旋转60°得到射线OB.(1)如图1,当点O运动到使点A在射线OP的左侧,若OA'平分∠POB,求∠BOF的度数;的值;(2)当点O运动到使点A在射线OP的左侧,且∠AOE=3∠A'OB时,求∠AOF∠AOP(3)当点O运动到某一时刻时,∠A'OB=130°,请直接写出∠BOP=_______度.21.(2022·福建·莆田华亭第一中学七年级期末)直线MN与直线PQ垂直相交于O,点A 在射线OP上运动,点B在射线OM上运动.(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB 的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;(2)如图2,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F,则∠EAF=______°;在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.22.(2022·内蒙古赤峰·七年级期末)如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM 在直线AB的下方.(1)将图1中的三角形板绕点O按照顺时针方向旋转至图2的位置,使得OM落在射线OA上,此时ON旋转的角度是____°;(2)继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置,使得OM在∠BOC的内部,则∠BON−∠COM=_____________°;(3)在上述直角板从图1旋转到图3的位置的过程中,若三角板绕点O按每秒钟15°的速度旋转,当OM恰好为∠BOC的平分线时,此时,三角板绕点O运动时间为__秒,并说明理由.23.(2022·福建三明·七年级期末)一副三角尺按照如图所示摆放在量角器上,边PD与量角器0刻度线重合,边AP与量角器180°刻度线重合,将三角尺ABP绕量角器中心点P以每秒4°的速度顺时针旋转,当边PB与0°刻度线重合时停止运动.设三角尺ABP的运动时间为t(秒)(1)当t=5秒时,边PB经过的量角器刻度线对应的度数为_ ;(2)t=秒时,边PB平分∠CPD;(3)若在三角尺ABP开始旋转的同时,三角尺PCD也绕点P以每秒1∘的速度逆时针旋转,当三角尺ABP停止旋转时,三角尺PCD也停止旋转,①当t为何值时,边PB平分∠CPD;②在旋转过程中,是否存在某一时刻,使得∠BPD:∠APC=3:2.若存在,请求出t的值;若不存在,请说明理由.24.(2022·福建·福州时代中学七年级期末)已知∠AOB=120°,OC、OD是过点O的射线,射线OM、ON分别平分∠AOC和∠DOB.(1)如图①,若OC、OD是∠AOB的三等分线,则∠MON=______°(2)如图②,若∠COD=40°,∠AOC≠∠DOB,则∠MON=______°(3)如图③,在∠AOB内,若∠COD=α(0°<α<60°),则∠MON=______°(4)将(3)中的∠COD绕着点O逆时针旋转到∠AOB的外部(0<∠AOC<180°,0<∠BOD< 180°),求此时∠MON的度数.25.(2022·全国·七年级课时练习)如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一直角边OM在射线OB上,另一直角边ON在直线AB的下方.(1)将图1中的三角板绕点O逆时针旋转至图2,使边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转过程中,第n 秒时,直线ON恰好平分∠AOC,则n的值为______(点接写结果)(3)若图1中的三角板绕点O旋转至图3,使ON在∠AOC的内部时,∠AOM−∠NOC的度数是多少?26.(2022·四川成都·七年级期末)如图1,点O为直线AB上一点,过点O作射线OC,OM,ON,ON始终在OM的右侧,∠BOC=112°,∠MON=α.(1)如图1,当α=70°,OM平分∠BOC时,求∠NOB的度数;(2)如图2,当OM与OB边重合,ON在OB的下方时,α=80°,将∠MON绕O点按每秒4°的速度沿逆时针方向旋转n(0°<n<180°),使射线ON与∠BOC的角平分线形成夹角为30°,求此时旋转一共用了多少秒;(3)当∠MON在直线AB上方时,若α=90°,点F在射线OB上,射线OF绕点O顺时针旋转n 度(0°<n<180°),恰好使得∠FOA=2∠AOM,OH平分∠NOC,∠FOH=124°,请直接写出此时n的值.27.(2022·山东临沂·七年级期末)定义:在同一平面内,有公共端点的三条射线中,一条射线是另两条射线组成夹角的角平分线,我们称这三条射线为“共生三线”.如图为一量角器的平面示意图,O为量角器的中心.作射线OA,OB,OC,并将其所对应的量角器内圈刻度....分别记为a°,b°,m°.(1)若射线OA,OB,OC为“共生三线”,且OC为∠AOB的角平分线.①如图1,a=0,b=80,则m=______;②当a=40,b=150时,请在图2中作出射线OA,OB,OC,并直接写出m的值;③根据①②的经验,得m=______.(用含a,b的代数式表示).(2)如图3,a=0,b=m=60.将OA,OB,OC按逆时针方向绕点O同时旋转,旋转速度分别为每秒10°,8°,6°,若旋转t秒后得到的射线OA′,OB′,OC′第一次成为“共生三线”,求t的值.28.(2022·福建莆田·七年级期末)将一副直角三角板AEF,AGH如图1摆放在直线PQ上,其中A,E,G三点在直线PQ上,三角板AEF在直线PQ上方,三角板AGH在直线PQ下方,∠GAH=90°,∠F AE=60°.(1)将三角板AGH从图1位置开始绕点A逆时针旋转至图2所示的位置,则∠HAE﹣∠F AG=_______;(2)若三角板AEF和三角板AGH同时从图1所示的位置分别以速度1、6(度/秒)绕点A逆时针旋转,问:经过多少秒后,AH和AF第一次重合;(3)三角板AGH旋转到直线PQ上方,点B在射线AQ上,若射线AB绕点A顺时针旋转n°(0<n<180),∠BAP=2∠P AG,AC平分∠HAF,当∠BAC=∠P AF时,求n的值.29.(2022·福建·厦门一中七年级期末)如图(1),∠BOC和∠AOB都是锐角,射线OB在∠AOC内部,∠AOB=α,∠BOC=β.(本题所涉及的角都是小于180°的角)(1)如图(2),OM平分∠BOC,ON平分∠AOC,填空:①当α=40°,β=70°时,∠COM=______,∠CON=______,∠MON=______;②∠MON=______(用含有α或β的代数式表示).(2)如图(3),P为∠AOB内任意一点,直线PQ过点O,点Q在∠AOB外部:①当OM平分∠POB,ON平分∠POA,∠MON的度数为______;②当OM平分∠QOB,ON平分∠QOA,∠MON的度数为______;(∠MON的度数用含有α或β的代数式表示)(3)如图(4),当α=40°,β=70°时,射线OP从OC处以5°/分的速度绕点O开始逆时针旋转一周,同时射线OQ从OB处以相同的速度绕点O逆时针也旋转一周,OM平分∠POQ,ON平分∠POA,那么多少分钟时,∠MON的度数是40°?30.(2022·北京·清华附中七年级期末)已知∠AOB=100°,∠COD=40°,OE,OF分别平分∠AOD,∠BOD.(1)如图1,当OA,OC重合时,∠EOF=度;(2)若将∠COD的从图1的位置绕点O顺时针旋转,旋转角∠AOC=α,满足0°<α<90°且α≠40°.①如图2,用等式表示∠BOF与∠COE之间的数量关系,并说明理由;②在∠COD旋转过程中,请用等式表示∠BOE与∠COF之间的数量关系,并直接写出答案.31.(2022·湖南长沙·七年级期末)如图1,在数轴上A、B两点对应的数分别是6,-6,∠DCE =90°(C与O重合,D点在数轴的正半轴上).(1)如图1,若CF平分∠ACE,则∠AOF=________;(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.①当t=1时,α=________;②猜想∠BCE和α的数量关系,并证明;(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴正半轴向右平移t(0<t<3)个单位,再绕顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α,β满足|α-β|=75°,请求出t的值.32.(2022·四川·达州市第一中学校七年级期末)如果两个角的差的绝对值等于60°,就称这两个角互为“伙伴角”,其中一个角叫做另一个角的“伙伴角”(本题所有的角都指大于0°小于180°的角),例如∠1=80°,∠2=20°,|∠1﹣∠2|=60°,则∠1和∠2互为“伙伴角”,即∠1是∠2的“伙伴角”,∠2也是∠1的“伙伴角”.(1)如图1,O为直线AB上一点,∠AOC=∠EOD=90°,∠AOE=60°,则∠AOE的“伙伴角”是;(2)如图2,O为直线AB上一点,∠AOC=30°,将∠BOC绕着点O以每秒1°的速度逆时针旋转得∠DOE,同时射线OP从射线OA的位置出发绕点O以每秒4°的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒;①当t为何值时,OD为∠AOC的角平分线;②当t为何值时,∠POD与∠POE互为“伙伴角”.33.(2022·安徽合肥·七年级期末)如图所示,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.(1)如图①,若∠AOC=28°,求∠DOE的度数;(2)在图①,若∠AOC=α,直接写出∠DOE的度数_________(用含a的代数式表示);(3)将图①中的∠COD绕顶点O顺时针旋转至图②的位置.①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;②在∠AOC的内部有一条射线OF,满足∠AOC−4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.34.(2022·河南·郑州市第四初级中学七年级期末)【阅读理解】如图①,射线OC在∠AOB内部,图中共有三个角∠AOC、∠AOB、∠BOC,若其中有两个角的度数之比为1:2,则称射线OC为∠AOB的“幸运线”.(1)∠AOB的角平分线这个角的“幸运线”;(填“是”或“不是”)(2)若∠AOB=120°,射线OC为∠AOB的“幸运线”,则∠AOC=.【问题解决】(3)如图②,已知∠AOB=150°,射线OP从OA出发,以20°/s的速度顺时针方向旋转,射线OQ从OB出发,以10°/s的速度逆时针方向旋转,两条射线同时旋转,当其中一条射线旋转到与∠AOB的边重合时,运动停止,设旋转的时间为t(s),当t为何值时,射线OP是以射线OA、OQ为边构成角的幸运线?试说明理由.∠AOC.35.(2022·湖北黄冈·七年级期末)已知:如图1,∠AOB=30°,∠BOC=34(1)求∠AOC的度数;(2)如图2,若射线OP从OA开始绕点O以每秒旋转10°的速度逆时针旋转,同时射线OQ从OB开始绕点O以每秒旋转6°的速度逆时针旋转;其中射线OP到达OC后立即改变运动方向,以相同速度绕O点顺时针旋转,当射线OQ到达OC时,射线OP,OQ同时停止运动.设旋转的时间为t秒,当∠POQ=10°时,试求t的值;(3)如图3,若射线OP从OA开始绕O点逆时针旋转一周,作OM平分∠AOP,ON平分∠COP,试求在运动过程中,∠MON的度数是多少?(请直接写出结果)36.(2022·湖北武汉·七年级期末)已知如图1,线段∠AOB=40°∠BOC,则∠BOC=_______________;(1)若∠AOC=13(2)如图2,∠AOC=20°,OM为∠AOB内部的一条射线,ON是∠MOC四等分线,且3∠CON=∠NOM,求4∠AON+∠COM的值;(3)如图3,∠AOC=20°,射线OM绕着O点从OB开始以5度/秒的速度逆时针旋转一周至OB 结束,在旋转过程中,设运动的时间为t,ON是∠MOC四等分线,且3∠CON=∠NOM,当t在某个范围内4∠AON+∠BOM会为定值,请直接写出定值,并指出对应t的范围(本题中的角均为大于0°且小于180°的角).37.(2022·浙江宁波·七年级期末)如图1,点O在直线AB上,过点O引一条射线OC,使∠AOC=50°,将一个直角三角尺的直角顶点放在点O处,直角边OM在射线OB上,另一边ON 在直线AB的下方.【操作一】:将图1中的三角尺绕着点O以每秒15°的速度按顺时针方向旋转.当它完成旋转一周时停止,设旋转的时间为t秒.(1)∠BOC的度数是___________,图1中与它互补的角是___________.(2)三角尺旋转的度数可表示为___________(用含t的代数式表示):当t=___________时,MO⊥OC.【操作二】:如图2将一把直尺的一端点也放在点O处,另一端点E在射线OC上.如图3,在三角尺绕着点O以每秒15°的速度按顺时针方向旋转的同时,直尺也绕着点O以每秒5°的速度按顺时针方向旋转,当一方完成旋转一周时停止,另一方也停止旋转,设旋转的时间为t秒.(3)当t为何值时,OM⊥OE,并说明理由?,是否存在某个时刻,使得∠COM (4)试探索:在三角尺与直尺旋转的过程中,当0≤t≤623与∠COE中其中一个角是另一个角的两倍?若存在,请求出所有满足题意的t的值;若不存在,请说明理由.38.(2022·重庆·七年级期末)如图1,∠AOB=40°,∠COD=60°,OM、ON分别为∠AOB和∠BOD的角平分线.。

七年级动点问题和动角问题培优训练一.动点问题1.对于数轴上的点M,线段AB,给出如下定义:P为线段AB上任意一点,如果M,P两点间的距离有最小值,那么称这个最小值为点M,线段AB的“近距”,记作d1(点M,线段AB);如果M,P两点间的距离有最大值,那么称这个最大值为点M,线段AB的“远距”,记作d2(点M,线段AB),特别的,若点M与点P重合,则M,P两点间距离为0,已知点A表示的数为﹣2,点B表示的数为3.例如图,若点C表示的数为5,则d1(点C,线段AB)=2,d2(点C,线段AB)=7.(1)若点D表示的数为﹣3,则d1(点D,线段AB)=,d2(点D,线段AB)=;(2)若点E表示数为x,点F表示数为x+1.d2(点F,线段AB)是d1(点E,线段AB)的3倍.求x的值.2.定义:当点P在线段AB上,AP=mAB时,我们称m为点P在线段AB上的“分值”,记作k P﹣AB=m.理解:如点P是AB的中点时,即,则AP=AB,则k P﹣AB=;反过来,当k P﹣AB=时,则有AP=AB.因此我们可以这样理解:”k P﹣AB=m”与”AP=mAB”具有相同的含义.应用:(1)如图1,点P在线段AB上.若k P﹣AB=,则AP=AB;若AP=4BP,则k P﹣AB=.(2)已知线段AB=27cm,点P,Q分别从点A、B同时出发,相向运动,点P到达点B 时,P,Q都停止运动,设运动时间为ts.①若点P,Q的运动速度均为1cm/s,试用含t的式子表示k P﹣AB和k Q﹣AB,并判断它们的数量关系;②若点P和点Q的运动速度分别为3cm/s和5cm/s,点Q到达点A后立即以原速返回B,t为何值时,k P﹣AB+k Q﹣AB=.拓展:(3)如图2,在三角形ABC中,AB=AC=12,BC=6,点P,Q同时从点A出发,点P沿线段AB匀速运动至点B.点Q沿线段AC,CB匀速运动至点B,且点P,Q同时到达点B,设k P﹣AB=m.当点Q运动到线段CB上时,请用含m的式子图2表示k Q﹣CB.3.【探索新知】如图1,点C将线段AB分成AC和BC两部分,若BC=πAC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.(1)若AC=3,求AB的值(用含π的代数式表示);(2)若点D也是图1中线段AB的圆周率点(不同于C点),求AC与DB的数量关系.【深入研究】如图2,现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点C的位置.(3)若点M、N均为线段OC的圆周率点,求线段MN的长度;(4)在图2中,点P、Q分别从点O、C位置同时出发,分别以每秒2个单位长度、每秒1个单位长度的速度向右匀速运动,运动时间为t秒.点P追上点Q时,停止运动,当P、C、Q三点中某一点为其余两点所构成线段的圆周率点时,请求出t的值.4.数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴时,我们发现有许多重要的规律:例如,若数轴上点A,B表示的数分别为a,b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点M表示的数为.如图,在数轴上,点A,B,C表示的数分别为﹣8,2,20.(1)如果点A和点C都向点B运动,且都用了4秒钟,那么这两点的运动速度分别是点A每秒个单位长度、点C每秒个单位长度;(2)如果点A以每秒1个单位长度沿数轴的正方向运动,点C以每秒3个单位长度沿数轴的负方向运动,设运动时间为t秒,请问当这两点与点B距离相等的时候,t为何值?(3)如果点A以每秒1个单位长度沿数轴的正方向运动,点B以每秒3个单位长度沿数轴的正方向运动,且当它们分别到达C点时就停止不动,设运动时间为t秒,线段AB的中点为点P;1.t为何值时PC=12;2.t为何值时PC=4.5.已知数轴上有A、B两点,点A表示的数为﹣8,且AB=20.(1)点B表示的数为;(2)如图1,若点B在点A的右侧,点P以每秒4个单位的速度从点A出发向右匀速运动.①若点Q同时以每秒2个单位的速度从点B出发向左匀速运动,经过多少秒后,点P与点Q相距1个单位?②若点Q同时以每秒2个单位的速度从点B出发向右匀速运动,经过多少秒后,在点P、B、Q三点中,其中有一点是另外两个点连接所成线段的中点?6.如图,在数轴上,点A表示﹣10,点B表示11,点C表示18.动点P从点A出发,沿数轴正方向以每秒2个单位的速度匀速运动;同时,动点Q从点C出发,沿数轴负方向以每秒1个单位的速度匀速运动.设运动时间为t秒.(1)当t为何值时,P、Q两点相遇?相遇点M所对应的数是多少?(2)在点Q出发后到达点B之前,求t为何值时,点P到点O的距离与点Q到点B的距离相等;(3)在点P向右运动的过程中,N是AP的中点,在点P到达点C之前,求2CN﹣PC 的值.7.已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s 的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值.(2)若点C、D运动时,总有MD=3AC,直接填空:AM=AB.(3)在(2)的条件下,N是直线AB上一点,且AN﹣BN=MN,求的值.8.已知a、b满足(a﹣2)2+|ab+6|=0,c=2a+3b,且有理数a、b、c在数轴上对应的点分别为A、B、C.(1)则a=,b=,c=.(2)点D是数轴上A点右侧一动点,点E、点F分别为CD、AD中点,当点D运动时,线段EF的长度是否发生变化,若变化,请说明理由,若不变,请求出其值;(3)若点A、B、C在数轴上运动,其中点C以每秒1个单位的速度向左运动,同时点A和点B分别以每秒3个单位和每秒2个单位的速度向右运动.请问:是否存在一个常数m使得m•AB﹣2BC不随运动时间t的改变而改变.若存在,请求出m和这个不变化的值;若不存在,请说明理由.9.已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x.(1)如果点P到点M点N的距离相等,则x=.(2)数轴上是否存在点P,使点P到点M、点N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.(3)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.10.如图1,已知数轴上A,B两点表示的数分别为﹣9和7.(1)AB=.(2)点P、点Q分别从点A、点B出发同时向右运动,点P的速度为每秒4个单位,点Q的速度为每秒2个单位,经过多少秒,点P与点Q相遇?(3)如图2,线段AC的长度为3个单位线段BD的长度为6个单位,线段AC以每秒4个单位的速度向右运动,同时线段BD以每秒2个单位的速度向左运动,设运动时间为t 秒.①t为何值时,点B恰好在线段AC的中点M处.②t为何值时,AC的中点M与BD的中点N距离2个单位.11.如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.问:(1)动点P从点A运动至C点需要多少时间?(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.12.有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是90米,甲、乙两机器人分别从A、B两点同时同向出发到终点C,乙机器人始终以50米分的速度行走,乙行走9分钟到达C点.设两机器人出发时间为t(分钟),当t=3分钟时,甲追上乙.请解答下面问题:(1)B、C两点之间的距离是米.(2)求甲机器人前3分钟的速度为多少米/分?(3)若前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,求两机器人前6分钟内出发多长时间相距28米?(4)在(3)的条件下,若6分钟后甲机器人的速度又恢复为原来出发时的速度,直接写出当t>6时,甲、乙两机器人之间的距离S.(用含t的代数式表示).二.动角问题13.如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB (其中∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒.(1)当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE 之间数量关系为;(2)若射线OC的位置保持不变,且∠COE=130°.①在旋转的过程中,是否存在某个时刻,使得射线OA,OC,OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意t的值,若不存在,请说明理由;②如图3,在旋转的过程中,边AB与射线OE相交,请直接写出∠AOC﹣∠BOE的值.14.将一副三角板中的含有60°角的三角板的顶点和另一块的45°角的顶点重合于一点O,绕着点O旋转60°的三角板,拼成如图的情况(OB在∠COD内部),请回答问题:(1)如图1放置,将含有60°角的一边与45°角的一边重合,求出此时∠AOD的度数.(2)绕着点O,转动三角板AOB,恰好是OB平分∠COD,此时∠AOD的度数应该是多少?(3)是否存在这种情况,∠AOC的度数恰好等于∠BOD度数的3倍.如果存在,请求出∠AOD的度数,如果不存在请说明理由.15.已知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.(1)如图1,若∠AOC=40°,求∠DOE的度数;(2)在图1中,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);(3)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置.①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;②在∠AOC的内部有一条射线OM,满足:4∠BOE﹣∠AOC=﹣3∠AOM,试确定∠AOM与∠DOE的度数之间的关系,说明理由.16.已知∠AOB=90°,∠COD=60°,按如图1所示摆放,将OA、OC边重合在直线MN 上,OB、OD边在直线MN的两侧:(1)保持∠AOB不动,将∠COD绕点O旋转至如图2所示的位置,则①∠AOC+∠BOD=;②∠BOC﹣∠AOD=.(2)若∠COD按每分钟5°的速度绕点O逆时针方向旋转,∠AOB按每分钟2°的速度也绕点O逆时针方向旋转,OC旋转到射线ON上时都停止运动,设旋转t分钟,计算∠MOC﹣∠AOD(用t的代数式表示).(3)保持∠AOB不动,将∠COD绕点O逆时针方向旋转n°(n≤360),若射线OE平分∠AOC,射线OF平分∠BOD,求∠EOF的大小.17.如图1,∠MON=90°,点A,B分别在射线OM、ON上.将射线OA绕点O沿顺时针方向以每秒9°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒3°的速度旋转(如图2).设旋转时间为t(0≤t≤40,单位秒).(1)当t=8时,∠AOB=°;(2)在旋转过程中,当∠AOB=36°时,求t的值.(3)在旋转过程中,当ON、OA、OB三条射线中的一条恰好平分另外两条射线组成的角(指大于0°而不超过180°的角)时,请求出t的值.18.如图,直线AB与CD相交于点O,OE是∠COB的平分线,OE⊥OF.(1)图中∠BOE的补角是;(2)若∠COF=2∠COE,求∠BOE的度数;(3)试判断OF是否平分∠AOC,并说明理由.19.【阅读新知】如图①,射线OC在∠AOB内,图中共有三个角∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角的度数的2倍,则称射线OC是∠AOB的“巧线”.【理解运用】(1)∠AOB的角平分线这个角的“巧线”;(填“是”或“不是”)(2)若∠AOB=90°,射线OC是∠AOB的“巧线”,则∠AOC的度数是.【拓展提升】如图②,一副三角板如图所示摆放在量角器上,边PD与量角器0°刻度线重合,边AP 与量角器180°刻度线重合,将三角板ABP绕量角器中心点P以每秒5°的速度顺时针方向旋转,当边PB与0°刻度线重合时停止运动,设三角板ABP的运动时间为t秒.(3)求t何值时,射线PB是∠CPD的“巧线”?(4)若三角板ABP按照原来方向旋转的同时,三角板PCD也绕点P以每秒2°的速度逆时针方向旋转,此时三角板ABP绕点P旋转的速度比原来每秒快了3°.当三角板ABP 停止旋转时,三角板PCD也停止旋转,问:在旋转过程中,是否存在某一时刻t,使三条射线PB、PC、PD中,其中一条恰好是以另两条组成的角的“巧线”?若存在,请直接写出t的值.若不存在,请说明理由.20.已知,OM平分∠AOC,ON平分∠BOC.(1)如图1,若OA⊥OB,∠BOC=60°,求∠MON的度数;(2)如图2,若∠AOB=80°,∠MON:∠AOC=2:7,求∠AON的度数.21.如图∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°,射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC与OD 同时旋转,设旋转时间为t分钟(t不超过15).(1)当t=时,射线OD与OC重合;(2)试探索:在射线OC与OD同时旋转过程中,是否存在某个时刻,使得射线OC平分∠BOD?若存在,请求出所有满足题意的t的值,若不存在,请说明理由;(3)t为何值时,射线OC与OD垂直.22.如图,点O在直线AB上,OC⊥AB.在Rt△ODE中,∠ODE=90°,∠DOE=30°,先将△ODE一边OE与OC重合(如图1),然后将△ODE绕点O按顺时针方向旋转(如图2),当OE与OB重合时停止旋转.(1)当∠AOD=80°时,则旋转角∠COE的大小为;(2)当OD在OC与OB之间时,求∠AOD﹣∠COE的值;(3)在△ODE的旋转过程中,若∠AOE=4∠COD时,求旋转角∠COE的大小.23.如图①,已知线段AB=20cm,CD=2cm,线段CD在线段AB上运动,E、F分别是AC、BD的中点.(1)若AC=4cm,则EF=cm.(2)当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变请求出EF的长度,如果变化,请说明理由.(3)我们发现角的很多规律和线段一样,如图②已知∠COD在∠AOB内部转动,OE、OF分别平分∠AOC和∠BOD,则∠EOF、∠AOB和∠COD有何关系,请直接写出.24.如图,OC是∠AOB内一条射线,OD、OE别是∠AOC和∠BOC的平分线.(1)如图①,当∠AOB=80°时,则∠DOE的度数为°;(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠BOE、∠EOD、∠DOA三角之间有怎样的数量关系?并说明理由;(3)当射线OC在∠AOB外如图③所示位置时,(2)中三个角:∠BOE、∠EOD、∠DOA之间数量关系的结论是否还成立?给出结论并说明理由;(4)当射线OC在∠AOB外如图④所示位置时,∠BOE、∠EOD、∠DOA之间数量关系是.。

2023-2024学年人教版七年级上册数学期末动角问题压轴题专题训练(1)若,则__________.(2)当线段在线段上运动时,试判断线段请求出线段的长度;如果变化,请说明理由.(3)我们发现角的很多规律和线段一样,如图2,已知(1)若,则 ;10cm AC =EF =cm CD AB EF EF 10cm AC =EF =cm(2)当线段在线段上运动时,试判断线段的长度是否会发生变化,如果不变,请求出线段的长度;如果变化,请说明理由;(3)我们发现角的很多规律和线段一样,如图2,已知在内部转动,分别平分和.类比以上发现的线段的规律,若,,求的度数.3.如图甲,已知线段,线段在线段上运动(不与端点、重合),E 、F 分别是、的中点.(1)观察发现:若,则______cm .(2)拓展探究:当线段在线段上运动时,试判断的长度是否发生变化?如果不变,求出的长度,如果变化,请说明理由.(3)迁移应用:对于角,也有和线段类似的规律:如图乙,在同一平面内,已知在内部转动,,分别平分和①若,,求;②请你猜想,和会有怎样的数量关系,直接写出你的结论.CD AB EF EF COD ∠AOB ∠OE OF 、AOC ∠BOD ∠80EOF ∠=︒35COD ∠=︒AOB ∠20cm AB =4cm CD =CD AB A B AC BD 6cm AC =EF =CD AB EF EF COD ∠AOB ∠OE OF AOC ∠BOD∠130AOB ∠=︒20COD ∠=︒EOF ∠EOF ∠AOB ∠COD ∠(1)当时,则线段 ,线段 .(2)用含的代数式表示运动过程中的长.(3)在运动过程中,若的中点为,问的长是否变化?与点的位置是否无关?(4)知识迁移:如图2,已知,过角的内部任一点画射线,若2t =AB =cm CD =cm t AB AB E EC B 120AOD ∠=︒B OB(1)如图1,为直线上的一点,,,直接写出图中一对垂角;(2)如果一个锐角的垂角等于这个角的余角的3倍,求这个角的度数;(3)如图2,为直线上的一点,若,,且射线绕以每秒的速度顺时针旋转,射线绕点以每秒的速度顺时针旋转,两条射线、同时运动,运动时间为秒,试求当为何值时,和互为垂角?6.如图①,已知线段在线段上运动,线段,,点、分别是、的中点.解答下列问题:(1)若,求的长;(2)当线段在线段上运动时,试判断的长度是否发生变化?如果不变请求出的长度,如果变化,请说明理由;(3)通过类比,我们发现角的很多规律和线段一样,如图②已知在内部转O AB =90AOC ︒∠90EOD ∠=︒O AB =90AOC ︒∠30BOD ∠=︒OC O 9︒OD O 6︒OC OD t ()030t <<t AOC ∠BOD ∠CD AB 10cm AB =2cm CD =E F AC BD 3cm AC =EF CD AB EF EF COD ∠AOB ∠动,和分别平分和,则与、有何数量关系,请直接写出答案.7.如图①,已知线段,线段在线段上运动(点A 不超过点M ,点B 不超过点N ),点C 和点D 分别是,的中点.(1)若,,求的长度;(2)若,线段运动时,试判断线段的长度是否发生变化?如果不变,请求出的长度,如果变化,请说明理由;(3)知识迁移:我们发现角的很多规律和线段一样,如图②,已知在内部转动,射线和射线分别平分和.当转动时,是否发生变化?,和三个角有怎样的数量关系,请说明理由.8.已知,为内部的一条射线,.OE OF AOC ∠BOD ∠EOF ∠AOB ∠COD ∠24cm MN =AB MN AM BN 8cm AM =2cm AB =CD 2cm AB a =AB CD CD AOB ∠MON ∠OC OD AOM ∠BON ∠AOB ∠COD ∠AOB ∠COD ∠MON ∠150AOB ∠=︒OC AOB ∠60BOC ∠=︒(1)运动开始前,如图1,∠AOM = °,∠DON = °;(2)旋转过程中,当t 为何值时,射线OB 平分∠AON ?(3)旋转过程中,是否存在某一时刻使得∠MON =35°?若存在,请求出t 的值;若不存AOC BOD∠∠参考答案:。

初中七年级(上)旋转动角问题专题(适用于七年级上学期)〖解题策略〗角是一种基本的几何图形,凡是由直线组成的图形都出现角. 角既可以看成有公共端点的两条射线组成的图形,也可以看成是一条射线绕着端点从一个位置旋转到另一个位置所成的图形.解与角有关的问题常用到以下知识与方法:1.角平分线的应用,如双角平分线模型;2. 多个角间的数量关系及其等量代换;3. 引入字母表示比例角度、动角,用方程的观点来进行角的计算;4.角的边位置不定时,需要分类讨论.〖典型例题〗已知∠AOB=150°,OC为∠AOB内部的一条射线,∠BOC=60°.(1)如图1,若OE平分∠AOB,OD为∠BOC内部的一条射线,∠COD=∠BOD,求∠DOE的度数;(2)如图2,若射线OE绕着O点从OA开始以15度/秒的速度顺时针旋转至OB结束、OF绕着O点从OB开始以5度秒的速度逆时针旋转至OA结束,运动时间为t秒,当∠EOC=∠FOC时,求t的值:(3)若射线OM绕着O点从OA开始以15度秒的速度逆时针旋转至OB结束,在旋转过程中,ON平分∠AOM,试问2∠BON一∠BOM在某时间段内是否为定值,若不是,请说明理由;若是请补全图形,求出这个定值并写出t所在的时间段.(本题中的角均为大于0°且小于180°的角)版权所有解:(1)∵∠AOB=150°,OE平分∠AOB,∴∠EOB=∠AOB=75°,∵∠BOC=60°,∠COD=∠BOD,∴∠BOD=40°,∠COD=20°,∴∠EOD=∠EOB﹣∠DOB=75°﹣40°=35°.(2)当OE在∠AOC内部时,∵∠EOC=∠FOC,∴90﹣15t=60﹣5t,∴t=3.当OE与OF重合时,15t+5t=150°,t=7.5.综上所述,当∠EOC=∠FOC时,t=3s或7.5s.(3)2∠BON﹣∠BOM的值为定值(4<t<12).理由:∵∠AOM=15t.∠AON=∠MON=7.5t,∠BON=210°﹣7.5t,∠BOM=210°﹣15t,∴2∠BON一∠BOM=2(210°﹣7.5t)﹣(210°﹣15t)=210°(4<t<12).〖同步练习〗一. 填空题.1.计算:53°40′30″+75°57′28″=2.同学们,闹钟都见过吧!它的时针和分针如同兄弟俩在赛跑,可你是否知道时针每分钟走多少度?分针每分针走多少度?当你弄清楚这个问题后,你能解决很多关于闹钟有趣的问题:(1)三点整时时针与分针所夹的角是度.(2)7点25分时针与分针所夹的角是度.(3)一昼夜(0点到24点)时针与分针互相垂直的次数有多少次?3.如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为.4.如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=°.二. 解答题5.如图,∠AOB=20°,∠AOE=110°,OB平分∠AOC,OD平分∠AOE.(1)求∠COD的度数;(2)若以点O为观察中心,OA为正东方向,求射线OD的方位角;(3)若∠AOE的两边OA,OE分别以每秒5°和每秒3°的速度,同时绕点O按逆时针方向旋转,当OA回到原处时,OA,OE停止运动,则经过多少秒时,∠AOE=30°?6.如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.(1)若∠AOC=100°,则∠DOE=;若∠AOC=120°,则∠DOE=;(2)若∠AOC=α,则∠DOE=(用含α的式子表示),请说明理由;(3)在∠AOC的内部有一条射线OF,满足∠AOC﹣2∠BOE=4∠AOF,试确定∠AOF与∠DOE的度数之间的关系,并说明理由.7.一副三角板ABC、DEF,如图(1)放置,(∠D=30°、∠BAC=45°)(1)求∠DBA的度数.(2)若三角板DBE绕B点逆时针旋转,(如图2)在旋转过程中BM、BN分别平分∠DBA、∠EBC,则∠MBN如何变化?(3)若三角板BDE绕B点逆时针旋转到如图(3)时,其它条件不变,则(2)的结论是否变化?8.如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(s).(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;(2)若在三角尺转动的同时,直线EF也绕点O以每秒9°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.①当t为何值时,EF平分∠AOB?②EF能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.9.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=;在图2中,OM是否平分∠CON?请说明理由;(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为(直接写出结果).10.如图1,在数轴上A,B两点对应的数分别是6,﹣6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)(1)如图1,若CF平分∠ACE,则∠AOF=;(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF 平分∠ACE,此时记∠DCF=α.①当t=1时,α=;②猜想∠BCE和α的数量关系,并证明;(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t (0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,请直接写出t的值为.〖参考答案〗一. 填空题.1.计算:53°40′30″+75°57′28″=129°37′58″,解:53°40′30″+75°57′28″=128°97′58″=129°37′58″2.同学们,闹钟都见过吧!它的时针和分针如同兄弟俩在赛跑,可你是否知道时针每分钟走多少度?分针每分针走多少度?当你弄清楚这个问题后,你能解决很多关于闹钟有趣的问题:(1)三点整时时针与分针所夹的角是90度.(2)7点25分时针与分针所夹的角是72.5度.(3)一昼夜(0点到24点)时针与分针互相垂直的次数有多少次?解:(1)3×30=90°;(2)2×30°=72.5°;(3)从重合到第一次垂直所需要的时间为,设一次垂直到下一次垂直经过x分钟,则6x﹣0.5x=2×905.5x=180x=,(24×60﹣)÷=24×60×=43.5(次)取整为43次.故总次数为43+1=44(次)答:一昼夜时针与分针互相垂直的次数为44次.3.如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为3或或.解:当∠NPQ=∠MPN时,15t=(75°+5t),解得t=3;当∠NPQ=∠MPN时,15t=(75°+5t),解得t=.当∠NPQ=∠MPN时,15t=(75°+5t),解得t=.故t的值为3或或.4.如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=114°.解:∵OC是∠AOB的平分线则∠AOC=∠BOC=∠AOB或∠AOB=2∠AOC=2∠BOC又∵剪开后得到的3个角中最大的一个角为76°,∴2∠COE=76°∴∠COE=38°又∵∠BOE=∠EOC,∴∠BOE=×38°=19°∴∠BOC=∠BOE+∠EOC=19°+38°=57°则∠AOB=2∠BOC=2×57°=114°.二. 解答题5.如图,∠AOB=20°,∠AOE=110°,OB平分∠AOC,OD平分∠AOE.(1)求∠COD的度数;(2)若以点O为观察中心,OA为正东方向,求射线OD的方位角;(3)若∠AOE的两边OA,OE分别以每秒5°和每秒3°的速度,同时绕点O按逆时针方向旋转,当OA回到原处时,OA,OE停止运动,则经过多少秒时,∠AOE=30°?解:(1)因为OB平分∠AOC,∠AOB=20°,所以∠AOC=40°,因为OD平分∠AOE,∠AOE=110°,所以∠AOD=55°,因为∠COD=∠AOD﹣∠AOC,所以∠COD=55°﹣40°=15°;(2)因为90°﹣55°=35°,所以射线OD的方位角是北偏东35°;(3)设经过x秒时,∠AOE=30°,①如图1所示,当OA未追上OE时,依题意,得5x﹣110=3x﹣30,解得,x=40;②如图2所示,当OA超过OE时,依题意,得5x﹣110=3x﹣305x﹣110=3x+30,解得,x=70.6.如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.(1)若∠AOC=100°,则∠DOE=50°;若∠AOC=120°,则∠DOE=60°;(2)若∠AOC=α,则∠DOE=α(用含α的式子表示),请说明理由;(3)在∠AOC的内部有一条射线OF,满足∠AOC﹣2∠BOE=4∠AOF,试确定∠AOF与∠DOE的度数之间的关系,并说明理由.解:(1)∵∠AOC=100°,∴∠BOC=180°﹣100°=80°,∵OE平分∠BOC,∴∠COE=∠BOC=×80°=40°,∵∠COD=90°,∴∠DOE=∠COD﹣∠COE=90°﹣40°=50°;∵∠AOC=120°,∴∠BOC=180°﹣120°=60°,∵OE平分∠BOC,∴∠COE=∠BOC=×60°=30°,∵∠COD=90°,∴∠DOE=∠COD﹣∠COE=90°﹣30°=60°;(2)∠DOE=α;∵∠AOC=α,∴∠BOC=180°﹣α,∵OE平分∠BOC,∴∠COE=∠BOC=90°﹣α,∵∠COD=90°,∴∠DOE=∠COD﹣∠COE=90°﹣(90°﹣α)=α;(3)∠DOE﹣∠AOF=45°.理由:∵∠AOC﹣2∠BOE=4∠AOF,∴∠AOC﹣3∠AOF=2∠BOE+∠AOF,设∠DOE=x,∠AOF=y,左边=∠AOC﹣3∠AOF=2∠DOE﹣3∠AOF=2x﹣3y,右边=2∠BOE+∠AOF=2(90°﹣x)+y=180°﹣2 x+y,∴2x﹣3y=180﹣2 x+y 即4x﹣4y=180°,∴x﹣y=45°∴∠DOE﹣∠AOF=45°.7.一副三角板ABC、DEF,如图(1)放置,(∠D=30°、∠BAC=45°)(1)求∠DBA的度数.(2)若三角板DBE绕B点逆时针旋转,(如图2)在旋转过程中BM、BN分别平分∠DBA、∠EBC,则∠MBN 如何变化?(3)若三角板BDE绕B点逆时针旋转到如图(3)时,其它条件不变,则(2)的结论是否变化?解:(1)∠DBA=∠DBC﹣∠ABC=60°﹣45°=15°;(2)∠MBN的度数不变化,理由如下:设∠ABE=x°,则∠ABD=60﹣x°、∠CBE=45°﹣x°,∵BM、BN分别平分∠ABD、∠CBE∴∠ABM=∠ABD=(60°﹣x°),∠EBN=∠EBC=(45°﹣x°),∴∠MBN=∠ABM+∠ABE+∠EBN=(60°﹣x°)+x°+(45°﹣x°)=52.5°;(3)(2)中的结论不变,理由如下:设∠ABE=x°,则∠ABD=60+x°、∠CBE=45°+x°,∵BM、BN分别平分∠ABD、∠CBE,∴∠ABM=∠ABD=(60°+x°),∠EBN=∠EBC=(45°+x°),∴∠MBN=∠ABM﹣∠ABE+∠EBN=(60°+x°)﹣x°+(45°+x°)=52.5°.8.如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(s).(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;(2)若在三角尺转动的同时,直线EF也绕点O以每秒9°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.①当t为何值时,EF平分∠AOB?②EF能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.解:(1)∵当直角边OB恰好平分∠NOE时,∠NOB=∠NOE=(180°﹣30°)=75°,∴90°﹣3t°=75°,解得:t=5.此时∠MOA=3°×5=15°=∠MOE,∴此时OA平分∠MOE.(2)①OE平分∠AOB,依题意有30°+9t﹣3t=90°÷2,解得t=2.5;OF平分∠AOB,依题意有30°+9t﹣3t=180°+90°÷2,解得t=32.5.故当t为2.5s或32.5s时,EF平分∠AOB②OB在MN上面,依题意有180°﹣30°﹣9t=(90°﹣3t)÷2,解得t=14;OB在MN下面,依题意有9t﹣(360°﹣30°)=(3t﹣90°)÷2,解得t=38(舍去).故EF能平分∠NOB,t的值为14s.9.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=90°;在图2中,OM是否平分∠CON?请说明理由;(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 4.5秒或40.5秒(直接写出结果).解:(1)如图2,∠BOM=90°,OM平分∠CON.理由如下:∵∠BOC=135°,∴∠MOC=135°﹣90°=45°,而∠MON=45°,∴∠MOC=∠MON;(2)∠AOM=∠CON.理由如下:如图3,∵∠MON=45°,∴∠AOM=45°﹣∠AON,∵∠AOC=45°,∴∠NOC=45°﹣∠AON,∴∠AOM=∠CON;(3)T=×45°÷5°=4.5(秒)或t=(180°+22.5°)÷5°=40.5(秒).10.如图1,在数轴上A,B两点对应的数分别是6,﹣6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)(1)如图1,若CF平分∠ACE,则∠AOF=45°;(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF 平分∠ACE,此时记∠DCF=α.①当t=1时,α=30°;②猜想∠BCE和α的数量关系,并证明;(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t (0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α,请直接写出t的值为.﹣β|=20°解:(1)如图1中,∵∠EOD=90°,OF平分∠EOD,∴∠FOD=∠EOD=45°,(2)①如图2中,当t=1时,∵∠DCA=30°,∠ECD=90°,∴∠ECA=120°,∵CF平分∠ACE,∴∠FCA=∠ECA=60°∴α=∠FCD=60°﹣30°=30°②如图2中,猜想:∠BCE=2α.理由:∵∠DCE=90°,∠DCF=α,∴∠ECF=90°﹣α,∵CF平分∠ACE,∴∠ACF=∠ECF=90°﹣α,∵点A,O,B共线∴AOB=180°∴∠BCE=∠AOB﹣∠ECD﹣∠ACD=180°﹣90°﹣(90°﹣2α)=2α.(3)如图3中,由题意:α=∠FCA﹣∠DCA=(90°+30t)﹣30t=45°﹣15t,β=∠AC1D1+∠AC1F1=30t+(90°﹣30t)=45°+15t,∵|β﹣α|=20°,,∴|30t|=20°解得t=.。
七上动角问题(难题)训练一、解答题1.如图,OM是∠AOC的平分线,ON是∠BOC的平分线.(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON=度。
(直接写出结果)(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON的度数是多少?为什么?2.已知线段AB=12cm,点C为AB上的一个动点,点D,E分别是AC和BC的中点,(1)若点C恰好是AB中点,求DE的长.(2)若AC=4cm,求DE的长.(3)试说明不论AC取何值(不超过12cm),DE的长不变.(4)知识迁移:如图2,已知∠AOB=120∘,过角的内部任一点C画射线OC,若OD,OE分别平分∠AOC和∠BOC,试说明∠DOE=60∘与射线OC的位置无关.3.如图1,已知PQ//MN,点A,B分别在MN,PQ上,且∠BAN=45°,射线AM绕点A顺时针旋转至AN便立即逆时针回转(速度是a/秒),射线BP绕点B顺时针旋转至BQ便立即逆时针回转(速度是秒).且a、b满足|a−3b|+(a+b−4)2=(1)直接写出a、b的值;(2)如图2,两条射线同时旋转,设旋转时间为t秒(t<60),两条旋转射线交于点C,过C作CD⊥AC交PQ于点D,求出∠BAC与∠BCD的数量关系;(3)若射线BP先旋转20秒,射线AM才开始旋转,设射线AM旋转时间为t秒(t≺160),若旋转中AM//BP,求t的值.4.如图1,已知∠AOC=120°,射线OM以每秒8°的速度,从射线OC开始逆时针向射线OA旋转,到达射线OA之后又以同样的速度顺时针返回,直到到达射线OC 停止,射线ON从射线OA开始,以每秒4°的速度顺时针向射线OC旋转,直到到达各自的目的地才停止.设旋转时间为t秒.(1)当t=5秒时,求出∠MON的度数.(2)在运动过程中,当∠MON达到48°时,求t的值.(3)在旋转过程中是否存在这样的t,使得射线OM、射线OA、射线ON其中一条射线是另外两条射线组成的角的角平分线?如果存在,请求出t的值;如果不存在,请说明理由.5.如图1,已知∠AOB=126°,∠COD=54°,OM在∠AOC内,ON在∠BOD内,∠AOM=1 3∠AOC,∠BON=13∠BOD.(1)∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,如图2,求∠MON 的度数;(2)∠COD从图2中的位置绕点O逆时针旋转n°(0<n<126且n≠54),求∠MON的度数;6.【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图甲所示的位置,请回答下面的问题.(1)如果重叠在一起∠BOC=30°,则∠AOD=___________.(2)若将∠COD绕点O旋转,使重叠在一起的∠BOC=50°,∠AOD=______ .(3)图甲中∠AOC与∠BOD满足的数量关系是___________,根据是__________.【拓展】在图甲所示的位置上,继续将∠COD绕点O旋转,得到如图乙所示的位置,请回答下面的问题.(4)如果∠BOC=x°,则∠AOD=_________________(用含x的式子表示)(5)此时图乙中∠AOC与∠BOD始终满足的数量关系是________________.【结论】由上述的探究过程可知,三角板COD绕重合点O旋转.不论旋转到任何位置时,∠AOD与∠BOC始终满足的数量关系是________________________.7.已知将一副三角板(直角三角板OAB和直角三角板OCD,∠AOB=900,∠ABO=450,∠CDO=900,∠COD=600)(1)如图1摆放,点O、A、C在一直线上,则∠BOD的度数是多少?(2)如图2,将直角三角板OCD绕点O逆时针方向转动,若要OB恰好平分∠COD,则∠AOC的度数是多少?(3)如图3,当三角板OCD摆放在∠AOB内部时,作射线OM平分∠AOC,射线ON平分∠BOD,如果三角板OCD在∠AOB内绕点O任意转动,∠MON的度数是否发生变化?如果不变,求其值;如果变化,说明理由.8.如图,已知直线AB上一点O,∠AOC=∠DOE=90°,∠DOC=∠EOB.(1)求证:∠AOD=∠COE证明(法1):∵∠AOC=∠DOE=90°(已知)∴∠AOD+∠COD=90°∠COE+∠COD=90°∴∠AOD=∠COE(____________)(法2)∵∠AOC=90°(已知)∴∠COB=90°∴∠AOD+∠DOC=90°∠COE+∠EOB=90°∵∠DOC=∠EOB(已知)∴∠AOD=∠COE(____________)∠BOD,求∠AOE、∠COD的度数.(2)若∠COE=159.已知如图(1):∠AOB=α,∠COD=β(3a>β,且α,β为锐角),OM平分∠AOD,ON平分∠COB,在线段AC上,AB=x,CD=y,M为AD中点,N为CB中点.(1)图(1)中,在∠AOC内,当射线OB和射线OD重合时,求∠MON的度数,此时在线段AC上,当点B和点D重合时,求线段MN的长度;(2)图(2)中,在∠AOC内,当射线OB和射线OD不重合时,求∠MON的度数,此时在线段AC上,当点B和点D不重合时,求线段MN的长度;(3)当∠COD从图(1)所示的位置绕点O逆时针旋转n∘(0<n<90)时,满足∠AOC+∠MON=6∠COD,求旋转度数n(结果用α,β表示)10.已知:如图,∠AOC=∠AOB+∠BOC,且∠AOC<180°,OD平分∠AOC,OE平分∠BOC.(1)如果∠AOB=80°,∠BOC=50°,求∠DOE的度数;(2)请你任意指定∠AOB和∠BOC的度数,其他条件不变,通过画图,计算∠DOE的度数;不必写出上述画图计算过程,直接写出你指定的∠AOB的度数为________°,∠BOC的度数为________°,算出的∠DOE的度数为________°;(3)在已知条件下,从(1)、(2)的结果中,你发现了什么规律,请写出来.11.将一副三角板中的两块直角三角尺的直角顶点C叠放在一起,其中∠A=60°,∠D=30°;∠E=∠B=45°.(1)①如图,若∠ACB=130°,求∠DCE的度数;②猜想∠ACB与∠DCE的数量关系,并说明理由;(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值;若不存在,请说明理由.12.如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线AB下方.(1)三角板绕点O逆时针旋转一定的角度,当边OM在∠BOC的内部,ON在AB的下方时,①若∠BON=10°,求∠COM的度数;②探究∠COM与∠BON之间的数量关系,并简单说明理由;(2)若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为(直接写出结果).13.O为直线AD上一点,以O为顶点作∠COE=90°,射线OF平分∠AOE.(1)如图①,∠AOC与∠DOE的数量关系为______ ,∠COF和∠DOE的数量关系为______;(2)若将∠COE绕点O旋转至图②的位置,OF依然平分∠AOE,请写出∠COF和∠DOE之间的数量关系,并说明理由;(3)若将∠COE绕点O旋转至图③的位置,射线OF依然平分∠AOE,请直接写出∠COF和∠DOE之间的数量关系.14.已知将一副三角板(∠AOB=90∘,∠ABO=45∘,∠CDO=90∘,∠COD=30∘):(1)如图1摆放,点O、A、C在一条直线上,求∠BOD的度数;(2)如图2,将直角三角板OCD绕点O逆时针方向转动,当OA恰好平分∠COD时,求∠BOC的度数;(3)如图3,继续旋转,当三角板OCD完全转入三角板AOB内部时,作射线OM平分∠AOD,射线ON平分∠BOC,①若∠AOD=20∘时,求∠MON的度数;②当∠AOD的度数改变时,∠MON的度数是否会改变,请说明理由.若不变,求出∠MON的值.15.如图1,点O为直线AB上一点,过点O作射线OC,将一直角三角形的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;(2)若∠BOC=120°.①将图1中的三角板绕点O按每秒12°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为__________(直接写出结果);②将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.16.如图,已知点O为直线MN上一点,点A在射线OM上,现将射线OA绕点O沿顺时针方向以每秒4°的速度旋转,OC为∠MOA的角平分线,点B为射线ON上的一点,射线OB绕点O沿逆时针方向以每秒6°的速度旋转,OD为∠BON的角平分线,OA、OB同时旋转,设旋转时间为t秒(0≤t≤60):⑴用含t的代数式表示∠AOC的度数.⑴在运动过程中,当∠COD第二次达到40°时,求t的值.⑴在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.17.点O是直线AB上一点,∠COD是直角,OE平分∠BOC.(1)①如图1,若∠DOE=25°,求∠AOC的度数;②如图2,若∠DOE=α,直接写出∠AOC的度数(用含α的式子表示);(2)将图1中的∠COD按顺时针方向旋转至图2所示的位置.探究∠DOE与∠AOC的度数之间的关系,写出你的结论,并说明理由.。
专题10几何图形初步中动角问题真题分类(解析版)专题简介:本份资料专攻《几何图形初步》这一章中动角问题的压轴题,所选题目源自各名校月考、期末试题中的压轴题真题,难度较大,具体分成单动角问题和双动角问题,适合于想挑战满分的学生考前刷题使用,也适合于培训机构的老师培训尖子生时使用。
题型一:单动角问题1.(雅礼)已知∠AOB=120°,∠COD=60°.(1)如图1,当∠COD在∠AOB的内部时,若∠AOD=98°,求∠BOC的度数;(2)如图2,当射线OC在∠AOB的内部,OD在∠AOB的外部时,试探索∠AOD与∠BOC的数量关系,并说明理由;(3)如图3,当∠COD在∠AOB的外部时,分别在∠AOC内部和∠BOD内部画射线OE,OF,使∠EOC=∠AOC,∠DOF=∠BOD,求∠EOF的度数.【解答】解:(1)∵∠AOB=120°,∠AOD=98°,∴∠BOD=∠AOB﹣∠AOD=120°﹣98°=22°,∵∠COD=60°,∴∠BOC=∠COD+∠BOD=60°+22°=82°;(2)∠AOD与∠BOC互补,理由:∵∠AOB+∠COD=120°+60°=180°,∠AOB=∠AOC+∠BOC,∠COD=∠BOC+∠BOD,∴∠AOB+∠COD=∠AOC+∠BOC+∠BOC+∠BOD=∠AOD+∠BOC=180°,∴∠AOD与∠BOC互补;(3)设∠BOC=n°,则∠AOC=∠AOB+∠BOC=120°+n°,∠BOD=∠COD+∠BOC=60°+n°,∵∠AOE=∠AOC,∴∠EOC=∠AOC=40°+n°.∵∠DOF=∠BOD,∴∠DOF=(60+n)=20°+n°,∴∠COF=∠COD﹣∠DOF=40°﹣n°,∴∠EOF=∠EOC+∠COF=40°+n°+40°﹣n°=80°.2.(长郡)已知∠AOB=100°,∠COD=40°,OE,OF分别平分∠AOD,∠BOD.(1)如图1,当OA ,OC 重合时,∠EOF =度;(2)若将∠COD 从图1的位置绕点O 顺时针旋转,旋转角∠AOC =α,满足0°<α<90°且α≠40°.①如图2,用等式表示∠BOF 与∠COE 之间的数量关系,并说明理由;②在∠COD 旋转过程中,请用等式表示∠BOE 与∠COF 之间的数量关系,并直接写出答案.【解答】解:(1)∵OA ,OC 重合,∴∠AOD =∠COD =40°,∠BOD =∠AOB +∠COD =100°+40°=140°,∵OE 平分∠AOD ,OF 平分∠BOD ,∴∠EOD =∠AOD =×40°=20°,∠DOF =∠BOD =×140°=70°,∴∠EOF =∠DOF ﹣∠EOD =70°﹣20°=50°;(2)①∠BOF +∠COE =90°;理由如下:∵OE 平分∠AOD ,OF 平分∠BOD ,∴∠EOD =∠AOE =∠AOD =(40°+α)=20°+α,∠BOF =∠BOD =(∠AOB +∠COD +α)=(100°+40°+α)=70°+α,∴∠COE =∠AOE ﹣∠AOC =20°+α﹣α=20°﹣α,∴∠BOF +∠COE =70°+α+20°﹣α=90°;②由①得:∠EOD =∠AOE =20°+α,∠DOF =∠BOF =70°+α,当∠AOC <40°时,如图2所示:∠COF =∠DOF ﹣∠COD =70°+α﹣40°=30°+α,∠BOE =∠BOD ﹣∠EOD =2(70°+α)﹣(20°+α)=120°+α,∴∠BOE ﹣∠COF =120°+α﹣(30°+α)=90°,当40°<∠AOC <90°时,如图3所示:∠COF =∠DOF +∠DOC =(360°﹣140°﹣α)+40°=150°﹣α,∠BOE =∠BOD ﹣∠DOE =140°+α﹣(20°+α)=120°+α,∴∠COF +∠BOE =150°﹣α+(120°+α)=270°;综上所述,∠BOE,∠COF,∠AOC之间的数量关系为∠BOE﹣∠COF=90°或∠COF+∠BOE=270°.3.(明德)如图①,已知线段MN=24cm,线段AB在线段MN上运动(点A不超过点M,点B不超过点N),点C和点D分别是AM,BN的中点.(1)若AM=8cm,AB=2cm,求CD的长度;(2)若AB=2acm,线段AB运动时,试判断线段CD的长度是否发生变化?如果不变,请求出CD的长度,如果变化,请说明理由.(3)知识迁移:我们发现角的很多规律和线段一样,如图②,已知∠AOB在∠MON内部转动,射线OC 和射线OD分别平分∠AOM和∠BON.当∠AOB转动时,∠COD是否发生变化?∠AOB,∠COD和∠MON 三个角有怎样的数量关系,请说明理由.【解答】解:(1)①∵MN=24cm,AB=2cm,AM=8cm,∴BN=MN﹣AB﹣AM=14(cm),∵点C和点D分别是AM,BN的中点,∴AC=AM=4cm,BD=BN=7cm.∴AC+BD=11(cm).∴CD=AC+AB+BD=11+2=13(cm).即CD的长为14cm.②不变,理由如下:∵点C和点D分别是AM,BN的中点,∴AC=AM,BD=BN,∴AC+BD=AM+BN=(AM+BN).又∵MN=24cm,AB=2acm,∴AM+BN=MN﹣AB=24﹣2a(cm).∴AC+BD=(AM+BN)=12﹣a(cm).∴CD=AC+AB+BD=12﹣a+2a=12+a(cm).(2)∠COD=(∠MON+AOB).理由如下:∵OC和OD分别平分∠AOM和∠BON,∴∠AOC =∠AOM ,∠BOD =∠BON .∴∠AOC +∠BOD =∠AOM +∠BON =(∠AOM +∠BON ).∴∠COD =∠AOC +∠BOD +∠AOB =(∠AOM +∠BON )+∠AOB =(∠MON ﹣∠AOB )+∠AOB =(∠MON +AOB ).4.(师大)若A 、O 、B 三点共线,∠BOC =50°,将一个三角板的直角顶点放在点O 处(注:∠DOE =90°,∠DEO =30°).(1)如图1,使三角板的短直角边OD 在射线OB 上,则∠COE =;(2)如图2,将三角板DOE 绕点O 逆时针方向旋转,若OE 恰好平分∠AOC ,则OD 所在射线是∠BOC 的;(3)如图3,将三角板DOE 绕点O 逆时针转动到使∠COD =∠AOE 时,求∠BOD 的度数;(4)将图1中的三角板绕点O 以每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t 秒时,OE 恰好与直线OC 重合,求t 的值.【解答】解:(1)∵∠DOE =90°,∠BOC =50°,∴∠COE =40°,故答案为40°;(2)∵OE 平分∠AOC ,∴∠AOE =∠COE ,∵∠COE +DOC =∠DOE =90°,∴∠AOE +∠DOB =90°,∴∠DOC =∠DOB ,∴DO 平分∠BOC ,∴DO 是∠BOC 的角平分线,故答案为:角平分线;(3)∵∠COD =∠AOE ,∠COD +∠DOE +∠AOE =130°,∴5∠COD =40°,∴∠COD =8°,∴∠BOD =58°;(4)当OE 与射线OC 的反向延长线重合时,5t +40=180,∴t =28,当OE 与射线OC 重合时,5t =360﹣40,∴t =64,综上所述:t 的值为28或64.5.(雅礼)如图1,点O 为直线AB 上一点,过点O 作射线OC ,使130BOC ∠=︒。
初中七年级(上)旋转动角问题专题(适用于七年级上学期)〖解题策略〗角是一种基本的几何图形,凡是由直线组成的图形都出现角. 角既可以看成有公共端点的两条射线组成的图形,也可以看成是一条射线绕着端点从一个位置旋转到另一个位置所成的图形.解与角有关的问题常用到以下知识与方法:1.角平分线的应用,如双角平分线模型;2. 多个角间的数量关系及其等量代换;3. 引入字母表示比例角度、动角,用方程的观点来进行角的计算;4.角的边位置不定时,需要分类讨论.〖典型例题〗已知∠AOB=150°,OC为∠AOB内部的一条射线,∠BOC=60°.(1)如图1,若OE平分∠AOB,OD为∠BOC内部的一条射线,∠COD=∠BOD,求∠DOE的度数;(2)如图2,若射线OE绕着O点从OA开始以15度/秒的速度顺时针旋转至OB结束、OF绕着O点从OB开始以5度秒的速度逆时针旋转至OA结束,运动时间为t秒,当∠EOC=∠FOC时,求t的值:(3)若射线OM绕着O点从OA开始以15度秒的速度逆时针旋转至OB结束,在旋转过程中,ON平分∠AOM,试问2∠BON一∠BOM在某时间段内是否为定值,若不是,请说明理由;若是请补全图形,求出这个定值并写出t所在的时间段.(本题中的角均为大于0°且小于180°的角)版权所有解:(1)∵∠AOB=150°,OE平分∠AOB,∴∠EOB=∠AOB=75°,∵∠BOC=60°,∠COD=∠BOD,∴∠BOD=40°,∠COD=20°,∴∠EOD=∠EOB﹣∠DOB=75°﹣40°=35°.(2)当OE在∠AOC内部时,∵∠EOC=∠FOC,∴90﹣15t=60﹣5t,∴t=3.当OE与OF重合时,15t+5t=150°,t=7.5.综上所述,当∠EOC=∠FOC时,t=3s或7.5s.(3)2∠BON﹣∠BOM的值为定值(4<t<12).理由:∵∠AOM=15t.∠AON=∠MON=7.5t,∠BON=210°﹣7.5t,∠BOM=210°﹣15t,∴2∠BON一∠BOM=2(210°﹣7.5t)﹣(210°﹣15t)=210°(4<t<12).〖同步练习〗一. 填空题.1.计算:53°40′30″+75°57′28″=2.同学们,闹钟都见过吧!它的时针和分针如同兄弟俩在赛跑,可你是否知道时针每分钟走多少度?分针每分针走多少度?当你弄清楚这个问题后,你能解决很多关于闹钟有趣的问题:(1)三点整时时针与分针所夹的角是度.(2)7点25分时针与分针所夹的角是度.(3)一昼夜(0点到24点)时针与分针互相垂直的次数有多少次?3.如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为.4.如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=°.二. 解答题5.如图,∠AOB=20°,∠AOE=110°,OB平分∠AOC,OD平分∠AOE.(1)求∠COD的度数;(2)若以点O为观察中心,OA为正东方向,求射线OD的方位角;(3)若∠AOE的两边OA,OE分别以每秒5°和每秒3°的速度,同时绕点O按逆时针方向旋转,当OA回到原处时,OA,OE停止运动,则经过多少秒时,∠AOE=30°?6.如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.(1)若∠AOC=100°,则∠DOE=;若∠AOC=120°,则∠DOE=;(2)若∠AOC=α,则∠DOE=(用含α的式子表示),请说明理由;(3)在∠AOC的内部有一条射线OF,满足∠AOC﹣2∠BOE=4∠AOF,试确定∠AOF与∠DOE的度数之间的关系,并说明理由.7.一副三角板ABC、DEF,如图(1)放置,(∠D=30°、∠BAC=45°)(1)求∠DBA的度数.(2)若三角板DBE绕B点逆时针旋转,(如图2)在旋转过程中BM、BN分别平分∠DBA、∠EBC,则∠MBN如何变化?(3)若三角板BDE绕B点逆时针旋转到如图(3)时,其它条件不变,则(2)的结论是否变化?8.如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(s).(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;(2)若在三角尺转动的同时,直线EF也绕点O以每秒9°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.①当t为何值时,EF平分∠AOB?②EF能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.9.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=;在图2中,OM是否平分∠CON?请说明理由;(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为(直接写出结果).10.如图1,在数轴上A,B两点对应的数分别是6,﹣6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)(1)如图1,若CF平分∠ACE,则∠AOF=;(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF 平分∠ACE,此时记∠DCF=α.①当t=1时,α=;②猜想∠BCE和α的数量关系,并证明;(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t (0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,请直接写出t的值为.〖参考答案〗一. 填空题.1.计算:53°40′30″+75°57′28″=129°37′58″,解:53°40′30″+75°57′28″=128°97′58″=129°37′58″2.同学们,闹钟都见过吧!它的时针和分针如同兄弟俩在赛跑,可你是否知道时针每分钟走多少度?分针每分针走多少度?当你弄清楚这个问题后,你能解决很多关于闹钟有趣的问题:(1)三点整时时针与分针所夹的角是90度.(2)7点25分时针与分针所夹的角是72.5度.(3)一昼夜(0点到24点)时针与分针互相垂直的次数有多少次?解:(1)3×30=90°;(2)2×30°=72.5°;(3)从重合到第一次垂直所需要的时间为,设一次垂直到下一次垂直经过x分钟,则6x﹣0.5x=2×905.5x=180x=,(24×60﹣)÷=24×60×=43.5(次)取整为43次.故总次数为43+1=44(次)答:一昼夜时针与分针互相垂直的次数为44次.3.如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为3或或.解:当∠NPQ=∠MPN时,15t=(75°+5t),解得t=3;当∠NPQ=∠MPN时,15t=(75°+5t),解得t=.当∠NPQ=∠MPN时,15t=(75°+5t),解得t=.故t的值为3或或.4.如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=114°.解:∵OC是∠AOB的平分线则∠AOC=∠BOC=∠AOB或∠AOB=2∠AOC=2∠BOC又∵剪开后得到的3个角中最大的一个角为76°,∴2∠COE=76°∴∠COE=38°又∵∠BOE=∠EOC,∴∠BOE=×38°=19°∴∠BOC=∠BOE+∠EOC=19°+38°=57°则∠AOB=2∠BOC=2×57°=114°.二. 解答题5.如图,∠AOB=20°,∠AOE=110°,OB平分∠AOC,OD平分∠AOE.(1)求∠COD的度数;(2)若以点O为观察中心,OA为正东方向,求射线OD的方位角;(3)若∠AOE的两边OA,OE分别以每秒5°和每秒3°的速度,同时绕点O按逆时针方向旋转,当OA回到原处时,OA,OE停止运动,则经过多少秒时,∠AOE=30°?解:(1)因为OB平分∠AOC,∠AOB=20°,所以∠AOC=40°,因为OD平分∠AOE,∠AOE=110°,所以∠AOD=55°,因为∠COD=∠AOD﹣∠AOC,所以∠COD=55°﹣40°=15°;(2)因为90°﹣55°=35°,所以射线OD的方位角是北偏东35°;(3)设经过x秒时,∠AOE=30°,①如图1所示,当OA未追上OE时,依题意,得5x﹣110=3x﹣30,解得,x=40;②如图2所示,当OA超过OE时,依题意,得5x﹣110=3x﹣305x﹣110=3x+30,解得,x=70.6.如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.(1)若∠AOC=100°,则∠DOE=50°;若∠AOC=120°,则∠DOE=60°;(2)若∠AOC=α,则∠DOE=α(用含α的式子表示),请说明理由;(3)在∠AOC的内部有一条射线OF,满足∠AOC﹣2∠BOE=4∠AOF,试确定∠AOF与∠DOE的度数之间的关系,并说明理由.解:(1)∵∠AOC=100°,∴∠BOC=180°﹣100°=80°,∵OE平分∠BOC,∴∠COE=∠BOC=×80°=40°,∵∠COD=90°,∴∠DOE=∠COD﹣∠COE=90°﹣40°=50°;∵∠AOC=120°,∴∠BOC=180°﹣120°=60°,∵OE平分∠BOC,∴∠COE=∠BOC=×60°=30°,∵∠COD=90°,∴∠DOE=∠COD﹣∠COE=90°﹣30°=60°;(2)∠DOE=α;∵∠AOC=α,∴∠BOC=180°﹣α,∵OE平分∠BOC,∴∠COE=∠BOC=90°﹣α,∵∠COD=90°,∴∠DOE=∠COD﹣∠COE=90°﹣(90°﹣α)=α;(3)∠DOE﹣∠AOF=45°.理由:∵∠AOC﹣2∠BOE=4∠AOF,∴∠AOC﹣3∠AOF=2∠BOE+∠AOF,设∠DOE=x,∠AOF=y,左边=∠AOC﹣3∠AOF=2∠DOE﹣3∠AOF=2x﹣3y,右边=2∠BOE+∠AOF=2(90°﹣x)+y=180°﹣2 x+y,∴2x﹣3y=180﹣2 x+y 即4x﹣4y=180°,∴x﹣y=45°∴∠DOE﹣∠AOF=45°.7.一副三角板ABC、DEF,如图(1)放置,(∠D=30°、∠BAC=45°)(1)求∠DBA的度数.(2)若三角板DBE绕B点逆时针旋转,(如图2)在旋转过程中BM、BN分别平分∠DBA、∠EBC,则∠MBN 如何变化?(3)若三角板BDE绕B点逆时针旋转到如图(3)时,其它条件不变,则(2)的结论是否变化?解:(1)∠DBA=∠DBC﹣∠ABC=60°﹣45°=15°;(2)∠MBN的度数不变化,理由如下:设∠ABE=x°,则∠ABD=60﹣x°、∠CBE=45°﹣x°,∵BM、BN分别平分∠ABD、∠CBE∴∠ABM=∠ABD=(60°﹣x°),∠EBN=∠EBC=(45°﹣x°),∴∠MBN=∠ABM+∠ABE+∠EBN=(60°﹣x°)+x°+(45°﹣x°)=52.5°;(3)(2)中的结论不变,理由如下:设∠ABE=x°,则∠ABD=60+x°、∠CBE=45°+x°,∵BM、BN分别平分∠ABD、∠CBE,∴∠ABM=∠ABD=(60°+x°),∠EBN=∠EBC=(45°+x°),∴∠MBN=∠ABM﹣∠ABE+∠EBN=(60°+x°)﹣x°+(45°+x°)=52.5°.8.如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(s).(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;(2)若在三角尺转动的同时,直线EF也绕点O以每秒9°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.①当t为何值时,EF平分∠AOB?②EF能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.解:(1)∵当直角边OB恰好平分∠NOE时,∠NOB=∠NOE=(180°﹣30°)=75°,∴90°﹣3t°=75°,解得:t=5.此时∠MOA=3°×5=15°=∠MOE,∴此时OA平分∠MOE.(2)①OE平分∠AOB,依题意有30°+9t﹣3t=90°÷2,解得t=2.5;OF平分∠AOB,依题意有30°+9t﹣3t=180°+90°÷2,解得t=32.5.故当t为2.5s或32.5s时,EF平分∠AOB②OB在MN上面,依题意有180°﹣30°﹣9t=(90°﹣3t)÷2,解得t=14;OB在MN下面,依题意有9t﹣(360°﹣30°)=(3t﹣90°)÷2,解得t=38(舍去).故EF能平分∠NOB,t的值为14s.9.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=90°;在图2中,OM是否平分∠CON?请说明理由;(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 4.5秒或40.5秒(直接写出结果).解:(1)如图2,∠BOM=90°,OM平分∠CON.理由如下:∵∠BOC=135°,∴∠MOC=135°﹣90°=45°,而∠MON=45°,∴∠MOC=∠MON;(2)∠AOM=∠CON.理由如下:如图3,∵∠MON=45°,∴∠AOM=45°﹣∠AON,∵∠AOC=45°,∴∠NOC=45°﹣∠AON,∴∠AOM=∠CON;(3)T=×45°÷5°=4.5(秒)或t=(180°+22.5°)÷5°=40.5(秒).10.如图1,在数轴上A,B两点对应的数分别是6,﹣6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)(1)如图1,若CF平分∠ACE,则∠AOF=45°;(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF 平分∠ACE,此时记∠DCF=α.①当t=1时,α=30°;②猜想∠BCE和α的数量关系,并证明;(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t (0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α,请直接写出t的值为.﹣β|=20°解:(1)如图1中,∵∠EOD=90°,OF平分∠EOD,∴∠FOD=∠EOD=45°,(2)①如图2中,当t=1时,∵∠DCA=30°,∠ECD=90°,∴∠ECA=120°,∵CF平分∠ACE,∴∠FCA=∠ECA=60°∴α=∠FCD=60°﹣30°=30°②如图2中,猜想:∠BCE=2α.理由:∵∠DCE=90°,∠DCF=α,∴∠ECF=90°﹣α,∵CF平分∠ACE,∴∠ACF=∠ECF=90°﹣α,∵点A,O,B共线∴AOB=180°∴∠BCE=∠AOB﹣∠ECD﹣∠ACD=180°﹣90°﹣(90°﹣2α)=2α.(3)如图3中,由题意:α=∠FCA﹣∠DCA=(90°+30t)﹣30t=45°﹣15t,β=∠AC1D1+∠AC1F1=30t+(90°﹣30t)=45°+15t,∵|β﹣α|=20°,,∴|30t|=20°解得t=.。
七上期末复习(压轴题)---动角问题训练一、解答题1.一副直角三角尺按如图①所示的方式摆放,∠C=∠DFE=90°,∠B=30°,∠E=45°,点F在BC上,点A在DF上,且AF平分∠CAB.现将三角尺DFE绕点F顺时针旋转(当点D落在射线FB上时停止旋转).(1)当∠AFD=________゜时,DF//AC;当∠AFD=________゜时,DF丄AB.(2)在旋转过程中,DF与交于点P,如图②.若△AFP有两个内角相等,求∠APD的度数.(3)当边DE与边AB、BC分别交于点M、N时,如图③.若∠AFM=2∠BMN,比较∠FMN与∠FNM的度数,并说明理由.2.已知:∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线.(1)如图1,若OM平分∠AOB,ON平分∠BOD.则∠MON的大小为______;(2)如图2,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD.求∠MON的大小;(3)在(2)的条件下,若∠AOB=10°,当∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒时,∠AOM:∠DON=2:3,求t的值.3.如图1,OC是∠AOB内的一条射线,(1)将OB、OA向∠AOB内部翻折,使射线OA、OB都与射线OC重合;折痕分别为OE、OF,∠EOF=25°,求∠AOB的度数;(2)如图2,∠MON=20°,OC是∠MON内部的一条射线,第一次操作分为两个步骤:第一步:将OC沿OM向∠MON外部翻折,得到OM1,第二步:将OC沿ON 向∠MON外部翻折,得到ON1;第二次操作也分为两个步骤:第一步:将OC沿OM1向∠MON外部翻折,得到OM2;第二步:将OC沿ON1向∠MON外部翻折,得到ON2;…依此类推,在第______ 次操作的第______ 步恰好第一次形成一个周角,并求∠MOC的度数.4.已知:点O为直线AB上一点,∠COD=90°,射线OE平分∠AOD.(1)如图①所示,若∠COE=20°,则∠BOD=______°.(2)若将∠COD绕点O旋转至图②的位置,试判断∠BOD和∠COE的数量关系,并说明理由;(3)若将∠COD绕点O旋转至图③的位置,∠BOD和∠COE的数量关系是否发生变化?并请说明理由.(4)若将∠COD绕点O旋转至图④的位置,继续探究∠BOD和∠COE的数量关系,请直接写出∠BOD和∠COE之间的数量关系:______.5.如图①,已知线段AB=20cm,CD=2cm,线段CD在线段AB上运动,E、F分别是AC、BD的中点.(1)若AC=4cm,则EF=______cm.(2)当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变请求出EF的长度,如果变化,请说明理由.(3)我们发现角的很多规律和线段一样,如图②已知∠COD在∠AOB内部转动,OE、OF分别平分∠AOC和∠BOD,则∠EOF、∠AOB和∠COD有何关系,请直接写出______.6.已知∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线.(1)如图1,若OM平分∠AOB,ON平分∠BOD.当OB绕点O在∠AOD内旋转时,求∠MON的大小;(2)如图2,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD.当∠BOC绕点O在∠AOD内旋转时,求∠MON的大小;(3)在(2)的条件下,若∠AOB=10°,当∠B0C在∠AOD内绕着点O以2度/秒的速度∠DON.求t的值.逆时针旋转t秒时,∠AOM=237.如图1,已知∠AOC=m°,∠BOC=n°且m、n满足等式|3m−420|+(2n−40)2=0,射线OP从OB处绕点0以4度/秒的速度逆时针旋转.(1)试求∠AOB的度数;(2)如图1,当射线OP从OB处绕点O开始逆时针旋转,同时射线OQ从OA处以1度/秒的速度绕点0顺时针旋转,当他们旋转多少秒时,使得∠POQ=10°;(3)如图2,若射线OD为∠AOC的平分线,当射线OP从OB处绕点O开始逆时针旋转,同时射线OT从射线OD处以x度/秒的速度绕点O顺时针旋转,使得这两条射线重合于射线OE处(OE在∠DOC的内部)时,且∠COE∠DOE+∠BOC =45,试求x.8.已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.(1)如图①,当OB、OC重合时,求∠AOE−∠BOF的值;(2)当∠COD从图①所示位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE−∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.9.已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;(2)当△AEF是直角三角形时,求a、b的值;(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由.已知O为直线AB上一点,射线OD,OC,OE位于直线AB上方,OD在OE的左侧,∠AOC=120°,∠DOE=80°.10.(1)如图,当OD平分∠AOC时,求∠EOB的度数;(2)点F在射线OB上,①若射线OF绕点O逆时针旋转n°(0<n<180且n≠60),∠FOA=3∠AOD,请判断∠FOE和∠EOC的数量关系并说明理由;②若射线OF绕点O顺时针旋转n°(0<n<180),∠FOA=2∠AOD,OH平分∠EOC,当∠FOH=∠AOC时,则n=____.11.如图1,在数轴上A,B两点对应的数分别是6,−6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)(1)如图1,若CF平分∠ACE,则∠AOF=______;(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.①当t=1时,α=______;②猜想∠BCE和α的数量关系,并证明;(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α−β|= 20°,请直接写出t的值为_______.12.如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)如图2,将图1中的三角板绕点O按逆时针方向旋转,使边OM在∠BOC的内部且OM恰好平分∠BOC,此时∠AOM的度数是多少?(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,求此时三角板绕点O旋转的时间是多少?13.一副三角尺按如图所示摆放在量角器上,边PD与量角器0°刻度线重合,边AP与量角器180°刻度线重合,将三角尺ABP绕量角器中心点P以每秒4°的速度顺时针旋转,当边PB与0°刻度线重合时停止运动,设三角尺ABP的运动时间为t.(1)当t=5时,边PB经过的量角器刻度线对应的度数是______度;(2)当t=______秒时,边PB平分∠CPD;(3)若在三角尺ABP开始旋转的同时,三角尺PCD也绕点P以每秒1°的速度逆时针旋转,当三角尺ABP停止旋转时,三角尺PCD也停止旋转.①当t为何值时,边PB平分∠CPD;②在旋转过程中,是否存在某一时刻使∠BPD=2∠APC,若存在,请直接写出t的值;若不存在,请说明理由.(1)如图1,若∠AOM=30°,求∠CON的度数;(2)在图1中,若∠AOM=a,直接写出∠CON的度数(用含a的代数式表示);(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,一边OM在射线OB上方,另一边ON在直线AB的下方.①探究∠AOM和∠CON的度数之间的关系,写出你的结论,并说明理由;②当∠AOC=3∠BON时,求∠AOM的度数.15.小明在学习过程中,对教材中的一个有趣问题做如下探究:【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;【探究廷伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.。