第十一章组合变形(习题解答)

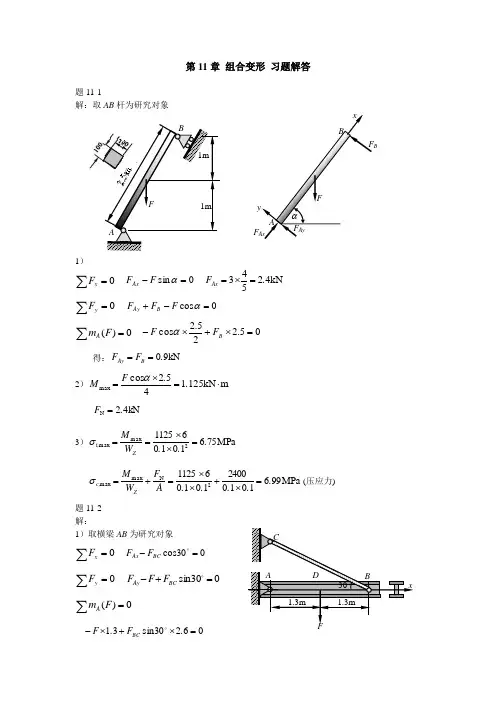
1mF1mB A 第11章 组合变形 习题解答题11-1解：取AB 杆为研究对象1）∑=0xF 0sin =-αF F Ax kN 42543.F Ax =⨯= ∑=0yF0cos =-+αF F F B Ay∑=0)(F m A 05.225.2cos =⨯+⨯-B F F α 得：kN 90.F F B Ay == 2）m kN 1251452cos max ⋅=⨯=..F M αkN 42N .F = 3）MPa 7561010611252max max ...W M Z t,=⨯⨯==σ MPa 996101024001010611252N max max .....A F W M Z c,=⨯+⨯⨯=+=σ(压应力) 题11-2解：1）取横梁AB 为研究对象∑=0xF 030cos =- BC Ax F F ∑=0yF030sin =+- BC Ay F F F ∑=0)(F mA06230sin 31=⨯+⨯-.F .F BCB1.3mx1.3mF ADC30F AxF AyFF Bαx y AB得：kN 30=BC F kN 26=Ax F kN 15=Ay F2）作内力图（略） 知：kN 26max N =Fm kN 5194max ⋅==.lF M3）查表得：N O 18工字钢 2cm 75630.A = 3cm 185=Z W则：MPa 91131075630102610185105194363Nmax max max ...A F W M σZ =⨯⨯+⨯⨯=+=--<MPa 160][=σ横梁强度足够题11-3 解：1） kN 15N ==F Fm kN 64015⋅=⨯=⨯=.e F M因 ][max σσ≤+=A FW M2）先按][max σσ≤=WM进行设计则633103532π106⨯≤⨯d 得：mm 5120.d = 3）代入拉弯组合应力公式校核MPa 2436120504π10151205032π1062333max ...A F W M =⨯⨯+⨯⨯=+=σ%6.3][][max =-σσσ<5%所以取 d =mm 5120.题11-4 解：1）内力分析kN 100N ==F F30m kN 502⋅=⨯=a aF M 2）应力分析6692max 10610)200(1805010)200(180650⨯≤⨯-⨯+⨯-⨯⨯⨯=+=--a a a AF W M σ得：mm 439.a ≤ 所以允许mm 439max .a =题11-5解：受力图略1）计算截面形心和ZC Imm 555381135138)553(113...y C =⨯⨯+⨯⨯⨯++⨯⨯=42323mm 6103138)51555(1238113)55558(12113.....I ZC =⨯⨯-+⨯+⨯⨯-+⨯=2）内力分析F F =N 310)55.526(-⨯+=F M3）确定夹紧力F410300][1055.563max ,⨯=≤⨯⨯+=-t ZC t I M A F σσ 得：N 400=F410600][1045.863max ,⨯=≤⨯⨯+-=-c ZC c I M A F σσ 得：N 7622.F =所以 N 400max =F题11-61）柱子受压弯组合，危险点为K 和K ′点（见图中所示）。

组合变形一、判断题1.斜弯曲区别与平面弯曲的基本特征是斜弯曲问题中荷载是沿斜向作用的。

( )2.斜弯曲时，横截面的中性轴是通过截面形心的一条直线。

( )3.梁发生斜弯曲变形时，挠曲线不在外力作用面内。

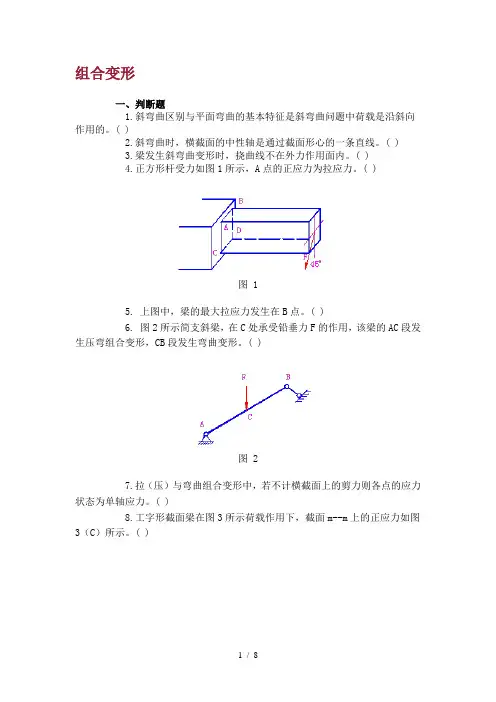
( )4.正方形杆受力如图1所示，A点的正应力为拉应力。

( )图 15. 上图中，梁的最大拉应力发生在B点。

( )6. 图2所示简支斜梁，在C处承受铅垂力F的作用，该梁的AC段发生压弯组合变形，CB段发生弯曲变形。

( )图 27.拉（压）与弯曲组合变形中，若不计横截面上的剪力则各点的应力状态为单轴应力。

( )8.工字形截面梁在图3所示荷载作用下，截面m--m上的正应力如图3（C）所示。

( )图 39. 矩形截面的截面核心形状是矩形。

( )10.截面核心与截面的形状与尺寸及外力的大小有关。

( )11.杆件受偏心压缩时，外力作用点离横截面的形心越近，其中性轴离横截面的形心越远。

( )12.计算组合变形的基本原理是叠加原理。

（）二、选择题1.截面核心的形状与（）有关。

A、外力的大小B、构件的受力情况C、构件的截面形状D、截面的形心2.圆截面梁受力如图4所示，此梁发生弯曲是（）图 4A、斜弯曲B、纯弯曲C、弯扭组合D、平面弯曲三、计算题1.矩形截面悬臂梁受力F1=F，F2=2F，截面宽为b，高h=2b，试计算梁内的最大拉应力，并在图中指明它的位置。

图 52.图6所示简支梁AB上受力F=20KN，跨度L=2.5m，横截面为矩形，其高h=100mm,宽b=60mm，若已知α=30°，材料的许用应力[σ]=80Mpa,试校核梁的强度。

3.如图7所示挡土墙，承受土压力F=30KN，墙高H=3m，厚0.75m，许用压应力[σ]ˉ=1 Mpa，许用拉应力[σ]﹢=0.1 Mpa，墙的单位体积重量为，试校核挡土墙的强度。

图 6 图 74.一圆直杆受偏心压力作用，其偏心矩e=20mm,杆的直径d=70mm,许用应力[σ]=120Mpa,试求此杆容许承受的偏心压力F之值。

L1AL101ADB 〔3〕偏心压缩时，截面的中性轴与外力作用点位于截面形心的两侧，那么外力作用点 到形心之距离ｅ和中性轴到形心距离ｄ之间的关系有四种答案：〔A 〕 ｅ＝ｄ； 〔B 〕 ｅ＞ｄ；〔C 〕 ｅ越小，ｄ越大； 〔D 〕 ｅ越大，ｄ越小。

正确答案是＿＿＿＿＿＿。

答案〔C 〕1BL102ADB 〔3〕三种受压杆件如图。

设杆１、杆２和杆３中的最大压应力〔绝对值〕分别用 max1σ、max 2σ和max3σ表示，现有以下四种答案：〔A 〕max1σ＝max 2σ＝max3σ； 〔B 〕max1σ＞max 2σ＝max3σ；〔C 〕max 2σ＞max1σ＝max3σ； 〔D 〕max 2σ＜max1σ＝max3σ。

正确答案是＿＿＿＿＿＿。

答案〔C 〕1BL103ADD 〔1〕在图示杆件中，最大压应力发生在截面上的哪一点，现有四种答案：〔A 〕Ａ点； 〔B 〕Ｂ点； 〔C 〕Ｃ点； 〔D 〕Ｄ点。

正确答案是＿＿＿＿＿＿。

答案〔C 〕1AL104ADC 〔2〕一空心立柱，横截面外边界为正方形， 边界为等边三角形〔二图形形心重 合〕。

当立柱受沿图示ａ－ａ线的压力时，此立柱变形形态有四种答案： 〔A 〕斜弯曲与中心压缩组合； 〔B 〕平面弯曲与中心压缩组合；〔C 〕斜弯曲； 〔D 〕平面弯曲。

正确答案是＿＿＿＿＿＿。

答案〔B 〕1BL105ADC 〔2〕铸铁构件受力如下图，其危险点的位置有四种答案：〔A 〕①点； 〔B 〕②点； 〔C 〕③点； 〔D 〕④点。

正确答案是＿＿＿＿＿＿。

答案〔D 〕1BL106ADC 〔2〕图示矩形截面拉杆中间开一深度为ｈ／２的缺口，与不开口的拉杆相比，开口处 的最大应力的增大倍数有四种答案：〔A 〕２倍； 〔B 〕４倍； 〔C 〕８倍； 〔D 〕１６倍。

正确答案是＿＿＿＿＿＿。

答案〔C 〕1BL107ADB 〔3〕三种受压杆件如图，设杆１、杆２和杆３中的最大压应力〔绝对值〕分别用 max1σ、max 2σ和max3σ表示，它们之间的关系有四种答案：〔A 〕max1σ＜max 2σ＜max3σ； 〔B 〕max1σ＜max 2σ＝max3σ；〔C 〕max1σ＜max3σ＜max 2σ； 〔D 〕max1σ＝max3σ＜max 2σ。

mnmn 第十一章的课后答案11-1 在计算行星轮系的传动比时，式i= 1- i H 只有在什么情况下才是正确的？mHmn答：在行星轮系，设固定轮为 n ，即ξ = 0 时， i= 1- i H 公式才是正确的。

nmHmn11-2 在计算周转轮系的传动比时，式i mH = (n m - n H )/ (n n - n H ) 中的i mH 是什么传动比，如何确定其大小和“ ± ”号？答：i mH 是在根据相对运动原理，设给原周转轮系加上一个公共角速度“ -ξH ”，使之绕 行星架的固定轴线回转，这时各构件之间的相对运动仍将保持不变。

而行星架的角速度为 0， 即行星架“静止不动”，于是周转轮系转化成了定轴轮系，这个转化轮系的传动比。

其大小可以用i mH = (n m - n H ) / (n n - n H ) 公式计算；方向由“ ± ”号确定，但注意，它由在转化轮系中m ，n两轮的转向关系来确定。

11-3 用转化轮系法计算行星轮系效率的理论基础是什么?为什么说当行星轮系为高速时，用它来计算行星轮系的效率会带来较大的误差？答：用转化轮系法计算行星轮系效率的理论基础是行星轮系的转化轮系和原行星轮系的差别，仅在于给整个行星轮系附加了一个公共角速度“ -ξH ”。

经过这样的转化之后，各构 件之间的相对运动没有改变，而轮系各运动副中的作用力（当不考虑构件回转的离心惯性力时）以及摩擦因数也不会改变。

因而行星轮系与其转化轮系中的摩擦损失功率应相等。

用转化轮系法计算行行轮系效率没有考虑由于加工、安装和使用情况等的不同，以及还有一些影响因素如搅油损失、行星轮在公转中的离心惯性力等，因此理论计算的结果并不能完全正确地反映传动装置的实际效率。

11-4 何谓正号机构、负号机均，各有何特点？各适用什么场合？答：行星轮系的转化轮系中当传动比i H > 0 ，称为正号机构；当传动比i H < 0 ，称为负号机构。

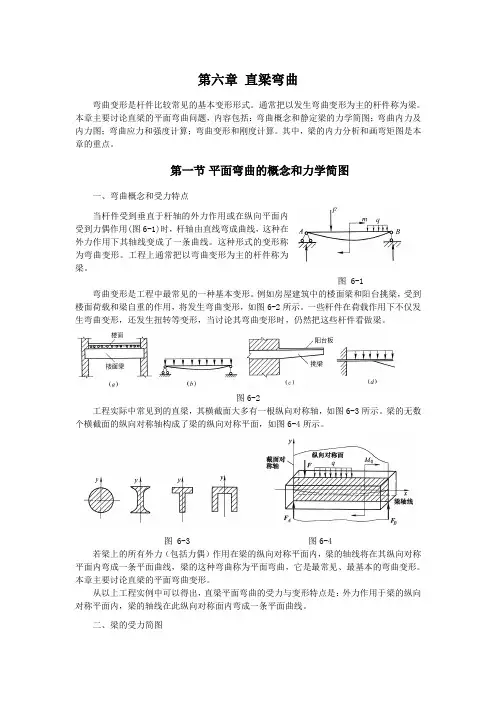
第六章直梁弯曲弯曲变形是杆件比较常见的基本变形形式。

通常把以发生弯曲变形为主的杆件称为梁。

本章主要讨论直梁的平面弯曲问题，内容包括：弯曲概念和静定梁的力学简图；弯曲内力及内力图；弯曲应力和强度计算；弯曲变形和刚度计算。

其中，梁的内力分析和画弯矩图是本章的重点。

第一节平面弯曲的概念和力学简图一、弯曲概念和受力特点当杆件受到垂直于杆轴的外力作用或在纵向平面内受到力偶作用(图6-1)时，杆轴由直线弯成曲线，这种在外力作用下其轴线变成了一条曲线。

这种形式的变形称为弯曲变形。

工程上通常把以弯曲变形为主的杆件称为梁。

图 6-1 弯曲变形是工程中最常见的一种基本变形。

例如房屋建筑中的楼面梁和阳台挑梁，受到楼面荷载和梁自重的作用，将发生弯曲变形，如图6-2所示。

一些杆件在荷载作用下不仅发生弯曲变形，还发生扭转等变形，当讨论其弯曲变形时，仍然把这些杆件看做梁。

图6-2工程实际中常见到的直梁，其横截面大多有一根纵向对称轴，如图6-3所示。

梁的无数个横截面的纵向对称轴构成了梁的纵向对称平面，如图6-4所示。

图 6-3 图6-4若梁上的所有外力（包括力偶）作用在梁的纵向对称平面内，梁的轴线将在其纵向对称平面内弯成一条平面曲线，梁的这种弯曲称为平面弯曲，它是最常见、最基本的弯曲变形。

本章主要讨论直梁的平面弯曲变形。

从以上工程实例中可以得出，直梁平面弯曲的受力与变形特点是：外力作用于梁的纵向对称平面内，梁的轴线在此纵向对称面内弯成一条平面曲线。

二、梁的受力简图为了便于分析和计算直梁平面弯曲时的强度和刚度，需建立梁的力学简图。

梁的力学简图（力学模型）包括梁的简化、荷载的简化和支座的简化。

1、梁的简化由前述平面弯曲的概念可知，载荷作用在梁的纵向对称平面内，梁的轴线弯成一条平面曲线。

因此，无论梁的外形尺寸如何复杂，用梁的轴线来代替梁可以使问题得到简化。

例如，图6-1a和图6-2a所示的火车轮轴和桥式起重机大梁，可分别用梁的轴线AB代替梁进行简化（图6-1b和图6-2b）。

组合变形1. 偏心压缩杆，截面的中性轴与外力作用点位于截面形心的两侧，则外力作用点到形心的距离e 和中性轴到形心的距离d 之间的关系有四种答案：(A) e d =； (B) e d >； (C) e 越小，d 越大； (D) e 越大，d 越大。

答：C2. 三种受压杆件如图所示，杆1、杆2与杆3中的最大压应力（绝对值）分别为max1σ、max 2σ和max 3σ，现有下列四种答案：(A)max1max 2max 3σσσ==； (B)max1max 2max 3σσσ>=； (C)max 2max1max 3σσσ>=； (D)max1max3σσσ<=max2。

答：C3.重合）。

立柱受沿图示a-a(A)斜弯曲与轴向压缩的组合； (B)平面弯曲与轴向压缩的组合； (C)斜弯曲； (D)平面弯曲。

答：B4. (A) A 点； (B) B 点； (C) C 点； (D) D 点。

答：C5. 图示矩形截面拉杆，中间开有深度为/2h 的缺口，与不开口的拉杆相比，开口处最大正应力将是不开口杆的 倍： (A) 2倍； (B) 4倍； (C) 8倍； (D) 16倍。

答：C6. 三种受压杆件如图所示，杆1、杆2与杆3中的最大压应力（绝对值）分别为max1σ、max 2σ和max 3σ，现有下列四种答案：(A)max1max 2max3σσσ<<； (B)max1max 2max3σσσ<=； (C)max1max3max 2σσσ<<； (D)max1max 3max 2σσσ=<。

答：C7. 正方形等截面立柱，受纵向压力F移至B 时，柱内最大压应力的比值max maxA B σσ(A) 1:2； (B) 2:5； (C) 4:7； (D) 5:2。

答：C8. 图示矩形截面偏心受压杆，其变形有下列四种答案：(A)轴向压缩和平面弯曲的组合； (B)轴向压缩、平面弯曲和扭转的组合； (C)缩和斜弯曲的组合；(D)轴向压缩、斜弯曲和扭转的组合。