第十一章组合变形

第十一章组合变形一、教学目标1、掌握组合变形的概念。

2、掌握斜弯曲、弯扭、拉（压）弯、偏心拉伸（压缩）等组合变形形式的概念和区分、危险截面和危险点的确定、应力计算、强度计算、变形计算、中性轴的确定等。

3、正确区分斜弯曲和平面弯曲。

4、了解截面核心的概念、常见截面的截面核心计算。

二、教学内容1、讲解组合变形的概念及组合变形的一般计算方法：叠加法。

2、举例介绍斜弯曲和平面弯曲的区别。

3、讲解斜弯曲的应力计算、中性轴位置的确定、危险点的确立、强度计算、变形计算。

4、讲解弯曲和扭转组合变形内力计算，确定危险截面和危险点，强度计算。

5、讲解拉伸(压缩)和弯曲组合变形的危险截面和危险点分析、强度计算。

6、讲解偏心拉伸(压缩)组合变形的危险截面和危险点分析、应力计算、强度计算。

7、简单介绍截面核心的概念和计算。

三、重点难点重点：斜弯曲、弯扭、拉（压）弯、偏心拉伸（压缩）等组合变形形式的应力和强度计算。

难点：1、解决组合变形问题最关键的一步是将组合变形分解为两种或两种以上的基本变形：斜弯曲——分解为两个形心主惯性平面内的平面弯曲；弯曲和扭转组合变形——分解为平面弯曲和扭转；拉伸（压缩）和弯曲组合变形——分解为轴向拉伸（压缩）和平面弯曲（因剪力较小通常忽略不计）；偏心拉伸（压缩）组合变形——单向偏心拉伸（压缩）时，分解为轴向拉伸（压缩）和一个平面弯曲，双向偏心拉伸（压缩）时，分解为轴向拉伸（压缩）和两个形心主惯性平面内的平面弯曲。

2、组合变形的强度计算，可归纳为两类：⑴危险点为单向应力状态：斜弯曲、拉（压）弯、偏心拉伸（压缩）组合变形的强度计算时只需求出危险点的最大正应力并与材料的许用正应力比较即可；⑵危险点为复杂应力状态：弯扭组合变形的强度计算时，危险点处于复杂应力状态，必须考虑强度理论。

四、教学方式采用启发式教学，通过提问，引导学生思考，让学生回答问题。

五、计划学时5学时六、讲课提纲(一)斜弯曲引言：*何谓平面弯曲？梁的弯曲平面与外力作用平面相重合的这种弯曲称为平面弯曲（或者说：梁的挠曲线是形心主惯性平面内的一条平面曲线）**平面弯曲与斜弯曲的比较(a) (b) (c)项目平面弯曲斜弯曲受力特点p F 平面与过y轴(形心主惯性轴)的纵平面重合pF平面过形心(这里也是弯心)但不与过y轴的纵平面重合。

第十一章 组合变形11.1 组合变形的概念11.1.1 组合变形图11-1在以前各章节中分别讨论了杆件拉伸〔压缩〕、剪切、扭转和弯曲等根本变形。

但工程实际中构造的某些构件往往同时承受几种根本变形。

例如，图11-1)(a 表示小型压力机的框架。

为分析框架立柱的变形，将外力向立柱的轴线简化，如图11-1)(b ，可见立柱承受了由F 引起的拉伸和由Fa M e 引起的弯曲。

这类由两种或两种以上根本变形组合的情况，称为组合变形。

11.1.2 叠加原理在组合变形中的应用图11-2在材料服从虎克定律且变形很小的前提下，杆件上虽然同时存在着几种根本变形，但每一种根本变形都是各自独立、互不影响的。

即任一根本变形都不会改变另一种变形所引起的应力和变形。

于是，分别计算每一种根本变形各自引起的应力和变形，然后求出这些应力和变形的总和，便是杆件在原载荷作用下的应力和变形，这就是叠加原理在组合变形中的应用。

上述叠加原理的成立，除材料必须服从虎克定律外，小变形的限制也是必要的。

现以压缩与弯曲的组合变形来说明这一问题。

当弯曲变形很小，可以忽略不计时，图(a，弯矩可以按杆件变形前的位置来计算。

这时轴向力P和横向载荷q的影响11-2)是各自独立的，叠加原理可以使用。

反之，假设杆件的抗弯刚度较小，弯矩应按杆件(b，那么轴向压力P除引起轴力外，还将产生弯矩Pv，变形后的位置计算，图11-2)而挠度v又受P及q的共同影响。

显然，压力P及横向载荷q的作用并不是各自独立的。

在这种情况下，尽管杆件仍然是线弹性的，但叠加原理也不能成立。

11.1.3 组合变形的几种常见方式1.斜弯曲2.拉伸或压缩与弯曲的组合3.扭转和弯曲的组合11.2 斜弯曲11.2.1 斜弯曲的概念由第7章知，仅当作用于构件上的横向力的作用线通过弯曲中心，且垂直于截面的一根形心主惯性轴时，构件才发生平面弯曲。

在工程实际中，作用在杆件上的横向力虽然通过弯曲中心，但有时并不垂直于截面的形心主轴。

第10章组合变形§10-1 组合变形的概念1.组合变形的概念组合变形：构件往往会发生两种或两种以上的基本变形的这类变形。

在前面各章分别讨论了杆件在拉(压)、剪切、扭转和弯曲基本变形时的应力和强度计算。

工程实际中，杆件在荷载作用下所发生的变形，经常是两种或两种以上基本变形的组合，这种变形称为组合变形。

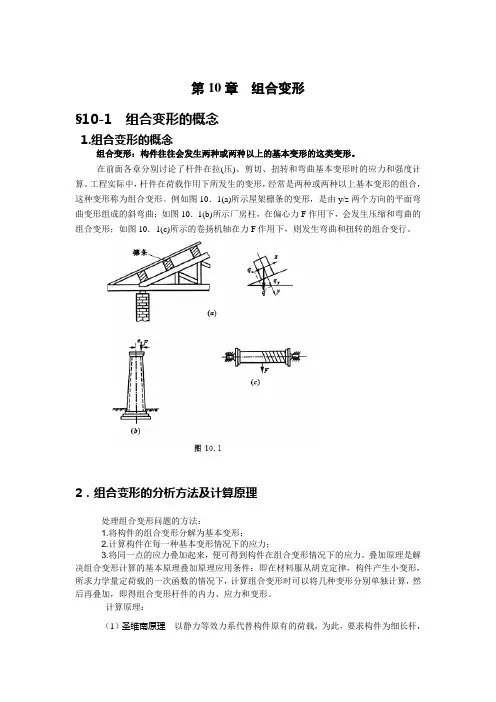
例如图10．1(a)所示屋架檩条的变形，是由y/z两个方向的平面弯曲变形组成的斜弯曲；如图10．1(b)所示厂房柱，在偏心力F作用下，会发生压缩和弯曲的组合变形；如图10．1(c)所示的卷扬机轴在力F作用下，则发生弯曲和扭转的组合变行。

2．组合变形的分析方法及计算原理处理组合变形问题的方法：1.将构件的组合变形分解为基本变形；2.计算构件在每一种基本变形情况下的应力；3.将同一点的应力叠加起来，便可得到构件在组合变形情况下的应力。

叠加原理是解决组合变形计算的基本原理叠加原理应用条件：即在材料服从胡克定律，构件产生小变形，所求力学量定荷载的一次函数的情况下，计算组合变形时可以将几种变形分别单独计算，然后再叠加，即得组合变形杆件的内力、应力和变形。

计算原理：（1）圣维南原理以静力等效力系代替构件原有的荷载，为此，要求构件为细长杆，且所求应力的截面远离外力作用点；（2）叠加原理 按各基本变形计算后进行叠加，为此，要求构件处于线弹性范围内，且变形很小，可按构件的原始形状的尺寸进行计算。

在小变形和线弹性条件下，杆件上各种力的作用彼此独立，互不影响，即杆上同时有几种力作用时，一种力对杆的作用效果（变形或应力），不影响另一种力对杆的作用效果（或影响很小可以忽略）。

因此组合变形下杆件内的应力，可视为几种基本变形下杆件内应力的叠加。

本章中组合变形下杆件的应力计算，将以各基本变形的应力及叠加法为基础。

叠加法的主要步骤：a 、将组合变形按照各基本变形的条件，分解为几种基本变形，简称分解。

b 、利用基本变形的应力计算公式，分别计算各点处的正应力和切应力。