当前位置：文档之家 › 材料力学第2版 课后习题答案 第11章 组合变形时的强度计算

材料力学第2版 课后习题答案 第11章 组合变形时的强度计算

  • 格式：pdf
  • 大小：467.88 KB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算

解：危险截面在 A 处，其上之内力分量为： 弯矩： M y = FP1 a ， M z = FP2 H 扭矩： M x = FP2 a 轴力： FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心， 面边界交于 a、b 两点，这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用，最 大压应力值大于最大拉应力值，故 b 点为危险点，其应力状态如图所示。 10－7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解： （a）为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10－9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10－9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试：
1．假定骨骼为实心圆截面，确定横截面 B－B 上的应力分布； 2．假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成，忽略海绵状承受 应力的能力，确定横截面 B－B 上的应力分布；

材料力学 第11章 组合变形习题集

材料力学 第11章 组合变形习题集

横截面m-m上任一点C(y，z)处由 弯矩Mz和My引起的正应力分别为
M z y M cos y M y z M sin z
Iz
Iz
Iy
Iy
38
C点的正应力
' ''
M
cos
Iz
y
sin
Iy
z
悬臂梁固定端截面A的弯矩Mz和My 均达到最大值，故该截
面是危险截面。设yo、zo为中性轴上任一点的坐标，并令σ
算 圆轴表面上与轴线成30°方位上的正应变。
32
解: (1)由内力图知，所有截面均为危险截面，危险点为靠近
轴表面的各点，应力状态如图。计算危险点的主应力。轴力
引起的正应力
FN 4F
A πd 2
扭矩引起的切应力
T M 8F
Wp Wp 5πd 2
危险点处的主应力为
1
2
(
)2
( )2
它在y、z两轴上的截距分别为
y* z* h / 2
该截面惯性半径的平方为
iy2
Iy A
h2 12
iz2
Iz A
b2 12
28
中性轴①对应的核心边界上点1的坐标为
ey1
iz2 y*
0
ez1
iy2 z*
h 6
按上述方法可求得与它们对应的截面核
心边界上的点2、3、4，其坐标依次为：
ey2
b 6
ez2 0
车臂的直径d。
18
解：两个缆车臂各承担缆车重量的一半，如 图。则缆车臂竖直段轴力为FN=W/2=3kN 弯矩为M=Wb/2=540N·m 危险截面发生在缆车臂竖直段左侧，由强度条件

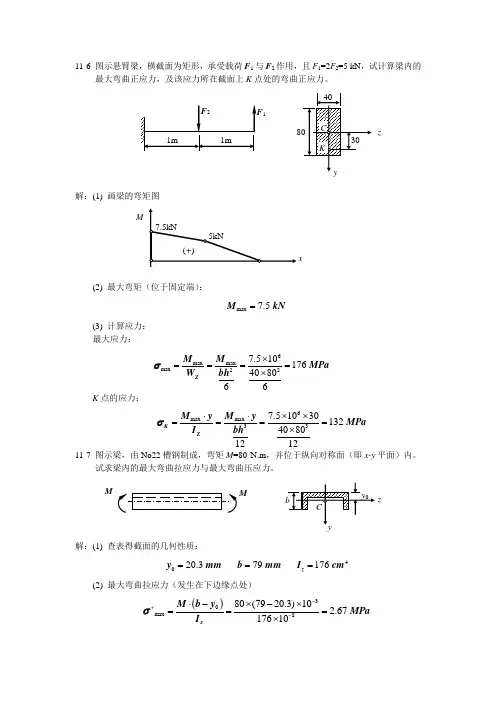
工程力学材料力学答案-第十一章

工程力学材料力学答案-第十一章

11-6 图示悬臂梁，横截面为矩形，承受载荷F 1与F 2作用，且F 1=2F 2=5 kN ，试计算梁内的最大弯曲正应力，及该应力所在截面上K 点处的弯曲正应力。

解：(1) 画梁的弯矩图(2) 最大弯矩（位于固定端）：max 7.5 M kN =(3) 计算应力： 最大应力：K 点的应力：11-7 图示梁，由No22槽钢制成，弯矩M =80 N.m ，并位于纵向对称面（即x-y 平面）内。

试求梁内的最大弯曲拉应力与最大弯曲压应力。

解：(1) 查表得截面的几何性质：4020.3 79 176 z y mm b mm I cm ===(2) 最大弯曲拉应力（发生在下边缘点处）()30max880(7920.3)10 2.67 17610x M b y MPa I σ-+-⋅-⨯-⨯===⨯6max max max227.510176 408066ZM M MPa bh W σ⨯====⨯6max max 337.51030132 ********K ZM y M y MPa bh I σ⋅⋅⨯⨯====⨯x M1zM M z(3) 最大弯曲压应力（发生在上边缘点处）30max88020.3100.92 17610x M y MPa I σ---⋅⨯⨯===⨯ 11-8 图示简支梁，由No28工字钢制成，在集度为q 的均布载荷作用下，测得横截面C 底边的纵向正应变ε=3.0×10-4，试计算梁内的最大弯曲正应力，已知钢的弹性模量E =200 Gpa ，a =1 m 。

解：(1) 求支反力31 44A B R qa R qa ==(2) 画内力图(3) 由胡克定律求得截面C 下边缘点的拉应力为：49max 3.010******* C E MPa σε+-=⋅=⨯⨯⨯=也可以表达为：2max4C C z zqa MW W σ+== (4) 梁内的最大弯曲正应力：2maxmax max 993267.5 8C zz qa M MPa W W σσ+====qxxF SM11-14 图示槽形截面悬臂梁，F =10 kN ，M e =70 kNm ，许用拉应力[σ+]=35 MPa ，许用压应力[σ-]=120 MPa ，试校核梁的强度。

材料力学答案2及材料力学答案第十一章

材料力学答案2及材料力学答案第十一章

习 题2-1 一木柱受力如图示，柱的横截面为边长20cm 的正方形，材料服从虎克定律，其弹性模量51010.0⨯=E MPa ．如不计柱自重，试求：（1）作轴力图； （2）各段柱横截面上的应力； （3）各段柱的纵向线应变； （4） 柱的总变形．解：（1） 轴力图（2） AC 段应力a a MP P σ5.2105.22.010100623-=⨯-=⨯-=CB 段应力a a MP P σ5.6105.62.010260623-=⨯-=⨯-=（3） AC 段线应变45105.2101.05.2-⨯-=⨯-==E σε N-图 CB 段线应变45105.6101.05.6-⨯-=⨯-==E σε （4） 总变形 m 3441035.15.1105.65.1105.2---⨯=⨯⨯-⨯⨯-=AB ∆2-2 图(a)所示铆接件，板件的受力情况如图（ｂ）所示．已知：P ＝7 kN ，t ＝0.15cm ，b 1＝0.4cm ，b 2=0.5cm ，b 3=0.6cml 。

试绘板件的轴力图，并计算板内的最大拉应力。

解:（2）a MP σ4.194101024.015.0767311=⨯⨯⨯⨯⨯=- a MP σ1.311101025.015.0767322=⨯⨯⨯⨯⨯=-a MP σ9.388101026.015.07673=⨯⨯⨯⨯=- 最大拉应力a MP σσ9.3883max ==2-3 直径为１cm 的圆杆，在拉力P ＝10 kN 的作用下，试求杆内最大剪应力，以及与横截面夹角为α＝30o 的斜截面上的正应力与剪应力。

解:（1） 最大剪应力a d MP ππP στ66.6310101102212672241max =⨯⨯⨯⨯===- （2）︒=30α界面上的应力()a MP ασσα49.952366.632cos 12=⨯=+= a MP αστα13.5530sin 66.632sin 2=⨯=⨯=︒ 2-4 图示结构中ABC 与CD 均为刚性梁，C 与D 均为铰接，铅垂力P ＝20kN 作用在C 铰，若（1）杆的直径d 1=1cm ，（2）杆的直径d 2=2cm ，两杆的材料相同，E ＝200Gpa ，其他尺寸如图示，试求（1）两杆的应力；（2）C 点的位移。

材料力学答案第十一章

材料力学答案第十一章

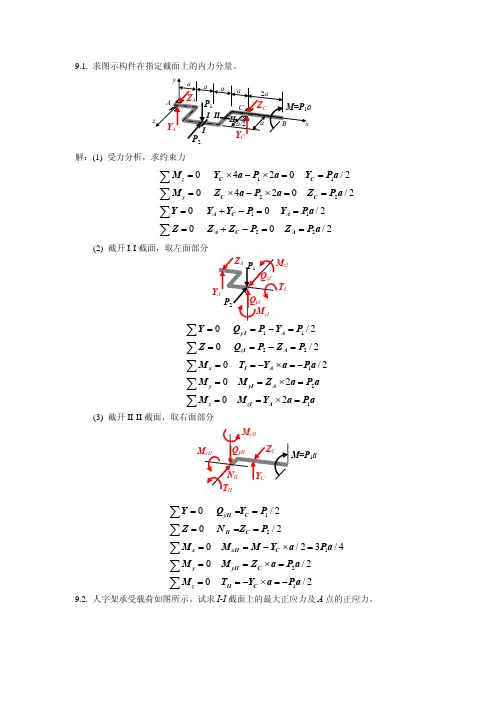
第十一章能量要领之阳早格格创做第十一章问案图示桁架各杆的资料相共，截里里积相等.试供正在F 力效率下，桁架的变形能.估计图示各杆的应变能.传动轴受力情况如图所示.轴的直径为40mm ，资料为45钢，E = 210GPa ，G = 80GPa.由扭转引起的应变能： 由蜿蜒引起的应变能：估计图示梁的应变能，并证明是可谦脚叠加本理及其本果.而没有谦脚叠加本理，果为应变能取内力的闭系没有是线性的.借帮于附录E ，供跨度中面（睹课本下册p40例12-4）11.6 图示刚刚架的各杆的EI 皆相等，试供截里A 、B 的位移战截里C 的转角.(a)A 面：正在A 面加一个背下的单位力.M (x 1)=0, M (x 2)=Fx 2, M (x 3)=FbC 面：正在C 加一个顺时针的力奇矩为１的单位力奇(b) A 面：正在A面加一个背下的单位力B 面：正在B 面加一个背左的单位力图示桁架各杆的资料相共，截里里积相等C 处的火仄位移战笔直位移.CF BAR火仄位移：(122) 3.828Fl FlEA EA +=-=-.笔直位移：Fl EA ∆=-.2，E 索 = 177GPa.F = 20kN ，(a)假设横梁ABCD 为刚刚体，供C 面的笔直位移.(2)若没有把ABCD 假设为刚刚体，且已知其抗直刚刚度为EI 2，试再供C 面的笔直位移.(1)42110.87.891033F EA -⎛⎫∆=⨯=⨯ ⎪⎝⎭m.(2)20.44047.89102Fx dx EI -∆=⨯+⎰4447.8910 1.48109.3710---=⨯+⨯=⨯m.11.9 等截里直杆BC 的轴线为四分之三的圆周.若AB 杆可视为刚刚性杆，试供正在F 力效率下，截里B 的火仄位移及笔直位移.火仄位移：M ()=FR cos, ()sin M R θθ=33320sin cos 2FR FRd EI EI πθθθ∆==⎰.D CFAB60 ° 60 ° 800 400400RFO B BF ORA F笔直位移：()(1cos )M R θθ=--33.36FR EI =.11.10 图示圆弧形小直率杆，仄衡半径为R .力F笔直于圆环中线地圆的仄里.试供二个F 力效率面的相对于线位移.M ()=FR sin, ()sin M R θθ= T ()=FR (1-cos), ()(1cos )T R θθ=-333pFR FR EI GI ππ=+.11.11图示圆弧形小直率杆，仄衡半径为R .正在横截里A 取B 处受一对于集结力F 效率.力F 正在圆环中线地圆的仄里内.试供二个F 力效率面的相对于线位移. M ()=FR sin,()sin M R θθ=32320sin FR FRd EI EI πθπθ∆==⎰.11.12图示轴线为火仄里内四分之一圆周的直杆，正在自由端B 效率笔直荷载F ，设EI 战GI P 为已知，试供正在F 力效率下端里B 的笔直位移.F O O Rθ B F AM ()=FR sin, ()sin M R θθ= T ()=FR (1-cos), ()(1cos )T R θθ=- 33(38)44pFR FR EI GI ππ-=+.。

材料力学习题解答(组合变形)

材料力学习题解答(组合变形)

N Mz
D C
D z 150 100
C z
My
Q
解：(1) 将力 P 和 H 向截面形心简化
M = 25 × 103 × 0.025 = 625 N .m
(2) 截面 ABCD 上的内力
N = − P = −25 kN M y = M = 625 N .m M z = H × 0.6 = 3 kN .m
N
如图作截面取上半部分，由静力平衡方程可得
N = P = 15kN
所以立柱发生拉弯变形。 (2) 强度计算 先考虑弯曲应力
上海理工大学 力学教研室
M = 0.4 P = 6kNm来自4σ t max =
d≥
M 32 M = ≤ [σ t ] πd3 W
3
π [σ t ]
32 M
=
3
32 × 6 × 103 = 120.4 mm π × 35 × 106
yc =
A1 y1c + A2 y2 c A
1.4 − 0.05 − 0.016 ⎞ ⎛ 1.204 × 0.7 + 1.105 × ⎜ 0.05 + ⎟ 2 ⎝ ⎠ = 0.51 m = 0.099
截面对形心轴的惯性矩
1 2 × 0.86 × 1.43 + ( 0.7 − 0.51) × 1.204 = 0.24 m 4 12 1 3 II I zc = × ( 0.86 − 2 × 0.016 ) × (1.4 − 0.05 − 0.016 ) 12
ZA YA P2
YC = P1a / 2 ZC = P2 a / 2
YA = P1a / 2 Z A = P2 a / 2
MzI
(2) 截开 I-I 截面，取左面部分 P1 QzI TI QyI MyI

复合材料力学答案

复合材料力学答案

复合材料力学答案【篇一：材料力学】教程第二版 pdf格式下载单辉祖主编本书是单辉祖主编《材料力学教程》的第2版。

是根据高等工业院校《材料力学教学基本要求》修订而成。

可作为一般高等工业院校中、少学时类材料力学课程的教材，也可作为多学时类材料力学课程基本部分的教材，还可供有关工程技术人员参考。

内容简介回到顶部↑本教村是普通高等教育“十五”国家级规划教材。

. 本教材仍保持第一版模块式的特点，由《材料力学(Ⅰ)》与《材料力学(Ⅱ)》两部分组成。

《材料力学(Ⅰ)》包括材料力学的基本部分，涉及杆件变形的基本形式与组合形式，涵盖强度、刚度与稳定性问题。

《材料力学(Ⅱ)》包括材料力学的加深与扩展部分。

本书为《材料力学(Ⅱ)》，包括非对称弯曲与特殊梁能量法(二)、能量法(二)、静不定问题分析、杆与杆系分析的计算机方法、应力分析的实验方法、疲劳与断裂以及考虑材料塑性的强度计算等八章。

各章均附有复匀题与习题，个别章还安排了利用计算机解题的作业。

..与第一版相同，本教材具有论述严谨、文字精炼、重视基础与应用、重视学生能力培养、专业面宽与教学适用性强等特点，而且，在选材与论述上，特别注意与近代力学的发展相适应。

本教材可作为高等学校工科本科多学时类材料力学课程教材，也可供高职高专、成人高校师生以及工程技术人员参考。

以本教材为主教材的相关教学资源，尚有《材料力学课堂教学多媒体课件与教学参考》、《材料力学学习指导书》、《材料力学网上作业与查询系统》与《材料力学网络课程》等。

...作译者回到顶部↑本书提供作译者介绍单辉祖，北京航空航天大学教。

1953年毕业于华东航空学院飞机结构专业，1954年在北京航空学院飞机结构专业研究生班学习。

1992—1993年，在美国特拉华大学复合材料中心．从事合作研究。

.历任教育部工科力学教材编审委员、国家教委工科力学课程指导委员会委员、中国力学学会教育工作委员会副主任委员、北京航空航天大学校务委员会委员、校学科评审组成员与校教学指导委员会委员等。

材料力学：第11章：组合变形

材料力学：第11章：组合变形

2
≤[σ]
2
M + 0.75T W
3
≤[σ]
πd
32
例：图示悬臂梁的横截面为等边三角形， 图示悬臂梁的横截面为等边三角形， C为形心，梁上作用有均布载荷ｑ，其作用方 为形心，梁上作用有均布载荷ｑ，其作用方 为形心 ｑ， 向及位置如图所示，该梁变形有四种答案： 向及位置如图所示，该梁变形有四种答案： A）平面弯曲； （√ ）平面弯曲； （C）纯弯曲； ）纯弯曲； （B）斜弯曲； ）斜弯曲； （D）弯扭结合。 ）弯扭结合。
Mz y My σ′=− =− sin ϕ Iz Iz
σ ′′ = −
ቤተ መጻሕፍቲ ባይዱ
My z Iy
Mz =− cos ϕ Iy
Py
Mz
Pz
My
y z σ = σ ′ + σ ′′ = − M sin ϕ + cos ϕ I Iy z
下面确定中性轴的位置： 下面确定中性轴的位置： 设中性轴上某一点的坐标为 y0 、 z0，则
α
ϕ
中性轴
ϕ
中性轴
二、位移计算 斜弯曲概念 为了计算梁在斜弯曲时的挠度， 为了计算梁在斜弯曲时的挠度，仍应用叠加法
fy = Py l
3
3EI Z
Pl3 = sin ϕ 3EI Z
Pl3 Pz l 3 fz = = cosϕ 3EI y 3EI y
ϕ
f =
2 fy
+f
2 z
tg β =
fy fz
=
Iy Iz
tg ϕ
tg β = tgα
α
β =α
ϕ
中性轴 总挠度f与中 总挠度 与中 性轴垂直

材料力学课后习题答案11章

材料力学课后习题答案11章

S z (η2 ) = 2.5 × 10 − 5 + (0.010η2 )(0.050 −
S z ,max (η 2 ) = 3.75 × 10 −5 m 3
η2
2
)
τ1 =
FSy S z , max (η1 ) 5 × 103 × 2.5 × 10 −5 N = = 3.75 × 106 Pa = 3.75MPa I zδ 3.333 × 10 − 6 × 0.010m 2 FSy S z , max (η2 ) I zδ 5 × 103 × 3.75 × 10 −5 N = = 5.63 × 106 Pa = 5.63MPa −6 2 3.333 × 10 × 0.010m
2 = 2.5 × 10 −5 + 2.5 × 10 −4 η 2 − 5 × 10 −3 η 2
τ 1, max =
FSy S z , max (η1 ) I zδ 1
=
5 × 103 × 1.25 × 10 −5 N = 3.00 ×106 Pa = 3.00MPa 2.08 × 10 − 6 × 0.010m 2
S z , A (ω ) =
δ
2 yA =
0.010 × 0.050 2 m 3 = 1.25 × 10 − 5 m 3 2
= 1.875 × 10 −4 m 3
据公式
τ (η ) =
得
FS S z (ω ) I zδ
40 × 10 3 × 1.25 × 10 −5 N τA = = 1.499 × 10 6 Pa = 1.499MPa −5 2 3.335 × 10 × 0.010m
[
]
11-6
试指出图示截面的剪心位置。
题 11-6 图 解： （a）双对称截面，剪心与形心重合； （b）角钢形截面，剪心在二边条中心线相交处； （c）T 形截面，剪心在翼缘中心线与腹板中心线相交处。

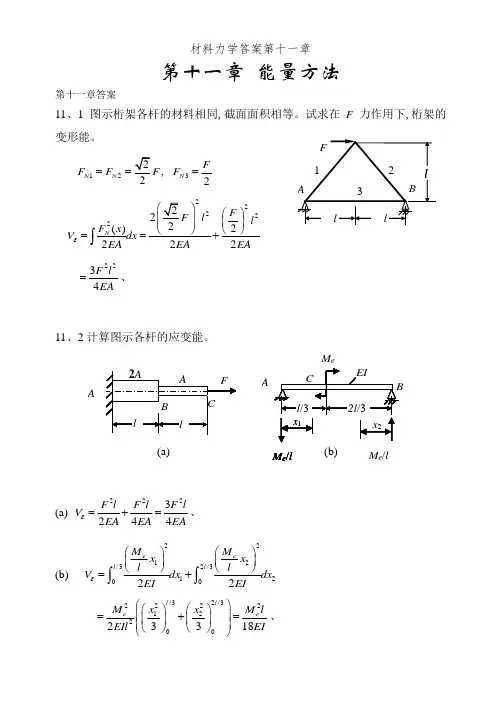
材料力学答案第十一章

材料力学答案第十一章

第十一章 能量方法第十一章答案11、1 图示桁架各杆的材料相同,截面面积相等。

试求在F 力作用下,桁架的变形能。

12,2N N F F F ==32N F F = 2222222()2222N F F l l F x V dx EA EA EA ε⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭==+⎰2234F l EA=、11、2计算图示各杆的应变能。

(a) 2223244F l F l F l V EA EA EAε=+=、 (b) 2212/32/3120022e e l l M M x x l l V dx dx EI EIε⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=+⎰⎰ /32/322221220023318l l e e M M l x x EIl EI ⎛⎫⎛⎫⎛⎫ ⎪=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭、11、3 传动轴受力情况如图所示。

轴的直径为40mm ,材料为45钢,E = 210GPa ,G = 80GPa 。

试计算轴的应变能。

由扭转引起的应变能:20.220800.0322pV dx GI ε==⎰由弯曲引起的应变能:20.210(531.4)20.0292x V dx EIε==⎰120.061J V V V εεε=+=、11、4 计算图示梁的应变能,并说明就是否满足叠加原理及其原因。

2230()26lFl Fx F lV dx EI EIε-==⎰而22310()22l Fl F lV dx EI EIε==⎰22320()26lFx F l V dx EI EIε-==⎰、不满足叠加原理,因为应变能与内力的关系不就是线性的。

、0、36kN(b)1kN200200 EIMe=FlFlx11、5在外伸梁的自由端作用力偶矩中点C 的挠度w c 。

(见课本下册p40例12-4)11、6 图示刚架的各杆的EI 皆相等,试求截面A 、B 的位移与截面C 的转角。

(a) A 点:在A 点加一个向下的单位力。

M (x 1)=0, M (x 2)=Fx 2, M (x 3)=Fb11()M x x =,22()M x Fx =,3()0M x = 3330()()h M x M x Fabhdx EI EI∆==-⎰、C 点:在C 加一个逆时针的力偶矩为１的单位力偶。

材料力学答案第十一章讲解学习

材料力学答案第十一章讲解学习

材料力学答案第十一章仅供学习与交流，如有侵权请联系网站删除 谢谢50第十一章 能量方法第十一章答案11.1 图示桁架各杆的材料相同，截面面积相等。

试求在F 力作用下，桁架的变形能。

12,2N N F F F == 32N F F = 222222()2222N F F l l F x V dx EA EA EA ε⎫⎛⎫⎪ ⎪⎝⎭⎝⎭==+⎰2234F l EA=.11.2计算图示各杆的应变能。

(a)仅供学习与交流，如有侵权请联系网站删除 谢谢512223244F l F l F l V EA EA EAε=+=.(b) 2212/32/3120022e e l l M M x x l l V dx dx EI EIε⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=+⎰⎰ /32/322221220023318l l ee M M l x x EIl EI ⎛⎫⎛⎫⎛⎫ ⎪=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.11.3 传动轴受力情况如图所示。

轴的直径为40mm ，材料为45钢，E = 210GPa ，G = 80GPa 。

试计算轴的应变能。

由扭转引起的应变能：20.220800.0322pV dx GI ε==⎰由弯曲引起的应变能：20.210(531.4)20.0292x V dx EIε==⎰120.061J V V V εεε=+=.11.4 计算图示梁的应变能，并说明是否满足叠加原理及其原因。

2230()26lFl Fx F l V dx EI EIε-==⎰0.08kN· 0.36kN (b) 1kN 2000200EIMe=FlFlx仅供学习与交流，如有侵权请联系网站删除 谢谢52而22310()22lFl F l V dx EI EIε==⎰22320()26lFx F l V dx EI EIε-==⎰.不满足叠加原理，因为应变能与内力的关系不是线性的。

11.5在外伸梁的自由端作用力偶矩M跨度中点C 的挠度w c 。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
∗ � 危险点： z = 10 ⋅ sin 43.77 = 6.918
cm cm
y ∗ = 10 ⋅ cos 43.77 � = 7.221 M max = 14 × 1 = 14 KN ⋅ m M y = M max ⋅ cos 45 � = 9.9 M z = M max ⋅ sin 45� = 9.9
M y max = σ max =
Pz l 2.59 × 3 = = 1.94 KN-M 4 4
M z max M y max + Wz Wy
7.25 × 10 3 1.94 × 10 3 = 3 + 10 × 10 −6 750 × 10 −6 = 9.84 MPa
中性轴：
⎛ J ⎞ α = tan −1 ⎜ − z tan ϕ ⎟ ⎜ Jy ⎟ ⎝ ⎠ 4 ⎛ 10 �⎞ ⎟ = tan −1 ⎜ − tan 15 ⎜ 5625 ⎟ ⎝ ⎠ = 25.47 �
B
60cm
C
10-9 图示起重结构，A 及 B 处可作铰链支承看待，C、D 与 E 均用销钉连结。AB 柱的 截面为 20cm × 30cm 的矩形。试求其危险截面上的最大正应力。 解：
R A = 25 × 2.4 / 3.6 = 16.6667
N = 25 KN
KN
M max = 25 × 10 3 × 2.4 − 16.667 × 2.4 × 10 3 = 20 A = 0.2 × 0.3 = 0.06 W=
在 S 截面： N = R A ⋅ cos α + (q ⋅ sin α ) ⋅ S =
1 (q ⋅ sin α ) + 1 A W
S=
l d l d + = + ⋅ tan α 0 2 8 cot α 0 2 8
10-11 某厂房柱子，受到吊车梁的铅垂轮压 P＝220 kN，屋 架传给柱顶的水平力 Q =8 kN，及风载荷 q＝1kN/m 的作用。P 力作用线离柱的轴线距离 e＝0.4m，柱子底部截面为矩形，尺 寸为 lm × 0.3m，试计算柱子底部危险点的应力。 解：
轴向分量： q ⋅ sin α 横向分量： q ⋅ cos α
∑MB = 0
RA = q ⋅ l ⋅ cos α 1 = ql cot α 2 sin α 2
1 ql ⋅ cot α ⋅ cos α + q ⋅ sin α × S 2 1 1 1 M ( s ) = ( R A ⋅ sin α ) ⋅ S − (q ⋅ cos α ) ⋅ S 2 = ql cot α sin α ⋅ S − q cos α ⋅ S 2 2 2 2 N M dσ σ = + ， =0 A W ds 1 cos α cos α ⎛1 ⎞ × × 2s ⎟ = 0 ⎜ q ⋅ l ⋅ cot α ⋅ sin α − q × 2 sin α sin α ⎝2 ⎠
MPa
10-14 正方形截面拉杆受拉力 P＝90kN 作 用 ， a＝5cm， 如在杆的根部挖去 1／4 如图示 。 试求杆内最大拉应力之值。 解：
tan α =
fz 1.95 = f y 0.305
, α = 81.1�
10-4简支梁的受力及横截面尺寸如图示。钢材的许用应力 [ σ ]＝160 MPa，试确定梁危 险截面中性轴的方向与校核此梁的强度。
解： J z =
π 4 bh 3 π 4 × 63 d − = × 10 4 − = 909.748 32 12 32 12
f = 0.5434 2 + 0.259 2 = 0.602 cm
方向 ⊥ 中性轴： α = 25.47
�
15cm
P2
h
b
10-3 矩形截面木材悬臂梁受力如图示， P1 ＝ 800 N ， P2 ＝ 1600 N 。材料许用应力 [σ]=10MPa，弹性模量 E＝10GPa，设梁截面的宽度 b 与高度 h 之比为 1：2。①试选择梁的 截面尺寸；②求自由端总挠度的大小和方向。 解： （ I） M z max = P2 × 1 = 1.6 KN
fy =
Py l 3
48 EJ z
=
9.66 × 10 3 × 33 = 0.5434 × 10 −2 m 9 4 −8 48 × 10 × 10 × 10 × 10
fz =
Pz l 3 2.59 × 10 3 × 33 = = 0.259 × 10 − 2 m 48 EJ y 48 × 10 × 10 9 × 5625 × 10 −8
= −146.2
MPa
σC =
My Mz ⋅ yA − ⋅ z A = −36.42 MPa J zO J yo My J yO
⋅ zB = 17.68 × 10 3 × 80.47 × 10 −3 = 120.56 −8 1180.04 × 10
σB =
MPa
10-6 旋臂 式 吊 车 梁 为 16 号工 字 钢 ， 尺 寸 如 图 所 示 ， 允 许 吊 重 P=10kN ，材 料 的 [ σ ]=160MPa。试校核吊车梁的强度。 解： B 点：
10-12 简单夹钳如图示。如夹紧力 P=6kN，材料的许用应力[ σ ]=140MPa。试校核其 强度。 解：
σ =
P Peb 6 × 10 3 6 × 6 × 10 3 × 6 × 10 −2 + 2 = + = 130 × 10 6 Pa = 130 MPa < [σ ] −4 2 −6 A bh 2 × 3 × 10 2 × 3 × 10
2.5 × 10 2 = 41.667cm 3 6
N M + ≤ [σ ] A W P = 120 × 10
6
⎛ 1 60 × 10 − 2 ⎞ ⎜ ⎟ + ⎜ 25 × 10 − 4 41.667 × 10 −6 ⎟ ⎝ ⎠
= 8108 N = 8.108 KN
最大应力点：
10-8 悬重构架如图所示，立柱 AB 系用 No25a 的工字钢制成。许用应力[ σ ]＝160 MPa， 在构架 C 点承受载荷 P＝20kN。①绘立柱 AB 的内力图；②找出危险截面，校核立柱强度； ③列式表示顶点 B 的水平位移。 解： （ i）
图
（II）
图
σ max =
N M 20 × 10 3 60 × 10 3 + = + = 153.42 × 10 6 Pa −4 −6 A W 48.5 × 10 401.883 × 10 = 153.42 MPa < [σ ]
P × 93 P × 6 2 (3 × 9 − 6) = 117 P (→) (III) f B = − 3EJ 6 EJ EJ
4
Pz = P sin ϕ = 10 × sin 15� = 2.59 KN Jz =
15 × 20 3 = 10 4 cm 4 12
W z = 10 3 cm 3 Jy =
20 × 153 = 5625 cm 3 12
W y = 750 cm 3 M z max = Py l
4 = 9.66 × 3 = 7.25 KN-M 4
0.2 × 0.3 2 = 0.003 6
KN ⋅ m
M2 M2
σ =
N M 25 × 10 3 20 × 10 3 + = + = 7.083 A W 0.06 0.003
M Pa
s
10-10 有一等直实心圆杆， 其 B 端为铰支承， A 端靠在光滑 的竖直墙面上（摩擦力可略去）如图示。杆长 L，杆截面直径d， 已知杆的总重 P 及倾角 α 。 试确定自 A 点至由于杆自重产生最 大压应力的横截面之距离 S。 解：设杆的自重为 q （N/M）
10-13 轮船上救生艇的吊杆尺寸及受力情况如图示， 图中载荷 W 系包括救生艇自重及被 救人员重量在内。试求其固定端 A-A 截面上的最大应力。 解：
N = 18
KN
M = 18 × 1.5 = 27 KN ⋅ m
σ =
N M 18 × 10 3 27 × 10 3 + = + = 160.75 A W π × 12 2 π × 12 2 −4 −6 × 10 × 10 4 32
Wy =
σ max =
b = 9 cm ， h = 18 cm
⎛ P × 2 3 ⎞ ⎛ P2 × 13 P2 × 13 ⎞ ⎟ +⎜ （II） f = ⎜ 1 + × 1⎟ 1.97 × 10 −2 m = 1.97cm ⎟ ⎜ 3EJ y ⎟ ⎜ 3EJ z 2 EJ z ⎠ ⎝ ⎠ ⎝源自2220cm
P × (1.08 + 1.94) = 15.57 KN 1.94 N 1.94 = H 0.8 1.94 H= × 15.57 = 37.76 KN 0.8 H=
No16 工字钢： A = 26.1cm
2
， J z = 1130cm
4
， W z 141cm
3
σ
max
=
N M 37.76 × 10 3 10 × 1.08 × 10 3 + = + = 91.1 A W 26.1 × 10 − 4 141 × 10 −6
M y max = P0 × 2 = 1.6 KN Wz = bh 2 b(2b) 2 2 3 = = b 6 6 3 bh 2 2b 3 1 3 = = b 6 6 3 M z max M y max 1.6 × 10 3 1.6 × 10 3 + = + ≤ [σ ] = 10 × 10 6 3 3 2 1 Wz WY b b 3 3
第十章
组合变形的强度计算
10-1 图示为梁的各种截面形状，设横向力 P 的作用线如图示虚线位置，试问哪些为平 面弯曲？哪些为斜弯曲？并指出截面上危险点的位置。