整式的恒等变换

第一章整式的运算(4)第一部分例题解析代数式的恒等变形是初中代数的重要内容，它是学好初中代数必备的基本功之一．两个代数式，如果对于字母在允许范围内的一切取值，它们的值都相等，则称这两个代数式恒等．把一个代数式变换成另一个与它恒等的代数式叫作代数式的恒等变形．恒等式的证明，就是通过恒等变形证明等号两边的代数式相等．一般可以把恒等式的证明分为两类：一类是无附加条件的恒等式证明；另一类是有附加条件的恒等式的证明．例1 已知x+y+z=xyz，证明：x(1-y2)(1-z2)+y(1-x2)(1-z2)+z(1-x2)(1-y2)=4xyz．“由繁到简”证因为x+y+z=xyz，所以左边=x(1-z2-y2-y2z2)+y(1-z2-x2+x2z2)+(1-y2-x2+x2y2)=(x+y+z)-xz2-xy2+xy2z2-yz2+yx2+yx2z2-zy2-zx2+zx2y2=xyz-xy(y+x)-xz(x+z)-yz(y+z)+xyz(xy+yz+zx)=xyz-xy(xyz-z)-xz(xyz-y)-yz(xyz-x)+xyz(xy+yz+zx)=xyz+xyz+xyz+xyz=4xyz=右边．例2 若abc=1，求证1111=++++++++ccacbbcbaaba评注：“1”的代换是恒等变形中常用的技巧。

例3 已知bc=ad，求证：ab(c2-d2)=(a2-b2)cd 利用比例的性质证明：∵bc=ad ∴a/b=c/d,(a+b)/b=(c+d)/d, (a-b)/b=(c-d)/d,c/d=c/d将此三式左、右两边分别相乘得∴ab(c2-d2)=(a2-b2)cd评注：条件恒等式的证明常从已知条件出发推出结论。

第二部分巩固练习1、计算（x2-3x+n）（x2+mx+8）的结果中不含x2和x3项，则m、n的值为（）BA、m=0，n=0B、m=3，n=1C、m=-3，n=8D、m=-3，n=-92、如果一个多项式与（2x-3）的积是4x2-12x+9，那么这个多项式是（）AA、2x-3B、4x2+9C、8x2-27D、2x+33、若 4a2-2ka+9是一个完全平方的展开形式，试求k的值：（）BA、12B、±6C、6D、±124、下列计算正确的有（）A①、（-4m2a）3=-64m6a3②、(2m2x3)2=4m2x6③、a m-n=a m-a n④、6a n+2÷3a n-1=2a ⑤、(-a3)2=-a6A、1个B、2个C、3个D、4个5、若a、b是有理数，且a 2001+b 2001=0，则ＣA、a=b=0B、a-b=0C、a+b=0D、ab=06、若abc满足a2+b2+c2=9，则代数式(a-b)2+(b-c)2+(c-a)2的最大值是( )A提示：(a+b+c)2≥0,得ab+bc+ca最小值A、27B、18C、15D、127、已知⎪⎩⎪⎨⎧+=+=+=200420012003200120022001x c x b x a ，则ca bc ab c b a ---++222的值是( )Ｄ A 、0 B 、1 C 、2 D 、38、如果11111=++=++z y x z y x ，则下列说法正确的是( ) Ａ提示：先用Z 表示x,y ，讨论中可得到(x-1)(y-1)=0A 、x 、y 、z 中至少有一个为1B 、x 、y 、z 都等于1C 、x 、y 、z 都不等于1D 、以上说法都不对 9、已知=+-=-+-+=-+-+=++-+q q q q b a c c b a a c b b a c c b a a c b 23 ,则( )Ｄ提示：q 3+q 2+q=A*B*C+A*B+A=1A 、1B 、1-qC 、1-q 3D 、1-2q 210、已知a+b+c=10，a 2+b 2+c 2=38，a 3+b 3+c 3=160，则abc 的值是( )BA 、24B 、30C 、36D 、42提示：先求ab+bc+ca,再利用a 3+b 3+c 3公式求abc,再(a 2+b 2+c 2)2,及a 2b 2+ b 2c 2+ c 2 a 2=( ab+ bc+ c a)2,最终可求a ４+b ４+c ４11、已知()()()=+≠--=-a c b a a c b a c b ，则且0 412 212、已知a-b=2，b-c= -3，c-d=5，则(a-c) (b-d) ÷ (a-d)= -1/213、已知abc ≠0，a+b+c=0，则211111b 1a +⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+b a c a c b c 的值为 提示：乘进去，再分组-114、计算⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-22221011911311211 = 11/20 15、已知a 、b 、c 、d 均不为0，当a ≠b 且a d dc c b b a ===时，=-+++++ad c b d c b a 0 第三部分 提高练习１、求证：2(a-b) (a-c)+2(b-c) (b-a)+2(c-a) (c-b)= (b-c)2+(c-a)2+(a-b)2２、求证：(a 2+b 2+c 2) (m 2+n 2+k 2) – (am+bn+ck)2=(an-bm)2+(bk-cn)2+(cm-ak)2(拉格朗日恒等式)３、若14(a 2+b 2+c 2)=(a+2b+3c)2，求证：a ∶b ∶c=1∶2∶3４、已知a、b、c、d满足a+b=c+d，a3+b3=c3+d3, 求证：a2001+b2001=c2001+d 2001提示：先用立方差公式得到a+b=c＋d=0,或ab=cd两种情况．第二种情况设ab=cd=m，代入a+b=c+d，分解因式．。

第8讲整式恒等变形模块一恒等变形→降幂迭代与换元基础夯实题型一降幂迭代法与大除法【例1】(第14届“希望杯”邀请赛试题)如果x2＋x－1＝0，那么x3＋2x2＋3＝__________．【练1】(1990年第一届希望杯初二第一试)已知3x2＋4x－7＝0，求6x4＋11x3－7x2－3x－7的值．题型二 整体代入消元法【例2】(第14届希望杯1试)若x ＋y ＝－1，求x 4＋5x 3y ＋x 2y ＋8x 2y 2＋xy 2＋5xy 3＋y 4的值．【练2】当x －y ＝1时，求x 4－xy 3－x 3y －3x 2y ＋3xy 2＋y 4的值．题型三 换元法强化挑战【例3】化简(y ＋z －2x )2＋(z ＋x －2y )2＋(x ＋y －2z )2－3(y －z )2－3(x －y )2－3(x －z )2．【练3】已知x ，y ，z 为有理数(y －z )2＋(z －x )2＋(x －y )2＝(y ＋z －2x )2＋(x ＋z －2y )2＋(x ＋y －2z )2，求()()()()()()222111111yz zx xy x y z ++++++的值．模块二 恒等变形→因式分解与不定方程题型一 因式分解基础夯实【例4】(1)已知a 5－a 4b －a 4＋a －b －1＝0，且2a －3b ＝1，则a 3＋b 3的值等于________．(2)若a 4＋b 4＝a 2－2a 2b 2＋b 2＋6，则a 2＋b 2＝________．【练4】(1)若x 满足x 5＋x 4＋x ＝－1则x ＋x 2＋x 3＋…＋x 2012＝__________．(2)已知15x 2－47xy ＋28y 2＝0，求x y的值．强化挑战【例5】已知：a 、b 、c 为三角形的三条边，且a 2＋4ac ＋3c 2－3ab －7bc ＋2b 2＝0，求证：2b ＝a ＋c ．【练5】(1)在三角形ABC 中，a 2－16b 2－c 2＋6ab ＋10bc ＝0，其中a ，b ，c 是三角形的三边，求证：a ＋c ＝2b ．(2)已知△ABC 三边a 、b 、c ，满足条件a 2c －a 2b ＋ab 2－b 2c ＋c 2b －ac 2＝0，试判断△ABC 的形状，并说明理由．题型二 不定方程【例6】(1)方程xy －2x －2y ＋7＝0的整数解(x ≤y )为___________．(2)已知a ＞b ＞c ≥0，求适合等式abc ＋ab ＋ac ＋bc ＋a ＋b ＋c ＝2011的整数a ，b ，c 的值．【练6】(1)长方形的周长为16cm ，它的两边长x ，y 均为整数，且满足x －y －x 2＋2xy －y 2＋2＝0，求它的面积．(2)矩形的周长28cm ，两边长为x cm 、y cm ，且x 3＋x 2y －xy 2－y 3＝0，求矩形的面积．【例7】(2000年联赛)实数x ，y 满足x ≥y ≥1和2x 2－xy －5x ＋y ＋4＝0，则x ＋y ＝_______．【练7】当x 变化时，分式22365112x x x x ++++的最小值是________．模块三 恒等变形→配方法【例8】已知x 2＋2xy ＋2y 2＋4y ＋4＝0，求x ，y ．【练8】已知x 2－6xy ＋10y 2－4y ＋4＝0，求x ，y ．【例9】已知x2＋2xy＋2y2＋4x＋8＝0，求x，y．【练9】已知x2－6xy＋10y2＋2x－8y＋2＝0，求x，y．【例10】已知实数a、b、c满足a－b＋c＝7，ab＋bc＋b＋c2＋16＝0．则ba的值等于____．【练10】已知a－b＝4，ab＋c2＋4＝0，则a＋b＝________．模块四恒等变形→乘法公式知识点睛【常见乘法公式】1、二元二次：(1)(a＋b)(a－b)＝__________．(2)(a－b)2＝__________．2、三元二次：(3)(a＋b＋c)2＝_________．(4)a2＋b2＋c2＋ab＋bc＋ca＝_______．3、二元三次：(5)(a＋b)3＝______________．(6)a3＋b3＝______________．4、三元三次：(7)(a＋1)(b＋1)(c＋1)＝abc＋ab＋bc＋ca＋a＋b＋c＋1(8)(a＋b)(b＋c)(c＋a)＝a2b＋b2c＋c2a＋ab2＋bc2＋ca2＋2abc(9)(a＋b＋c)(ab＋bc＋ca)＝a2b＋b2c＋c2a＋ab2＋bc2＋ca2＋3abc(10)a3＋b3＋c3－3abc＝(a＋b＋c)(a2＋b2＋c2－ab－bc－ca)5、三元四次：(11)(a＋b＋c)(a＋b－c)(b＋c－a)(c＋a－b)＝－a4－b4－c4＋2a2b2＋2b2c2＋2c2a26、二元n次：(12)a n－b n＝(a－b)(a n－1＋a n－2b＋a n－3b2＋…＋ab n－2＋b n－1)(13)a n＋b n＝(a＋b)(a n－1－a n－2b＋a n－3b2＋…－ab n－2＋b n－1)(n为奇数)7、n元二次：(14)(a1＋a2＋…＋a n)2＝a12＋a22＋…＋a n2＋2a1a2＋2a1a3＋…＋2a1a n＋2a2a3＋2a2a4＋…＋2a n－1a n．(15)a12＋…＋a n2＋a1a2＋…＋a1a n＋a2a3＋…＋a2a n＋…＋a n－1a n＝1[(a1＋a2)2＋…＋(a n－1＋a n)2]强化挑战【例11】已知实数a、b、x、y满足a＋b＝x＋y＝3，ax＋by＝4，求(a2＋b2)xy＋ab(x2＋y2)的值．【练11】(第6届希望杯初一)已知ax＋by＝7，ax2＋by2＝49，ax3＋by3＝133，ax4＋by4＝406，试求1995(x＋y)＋6xy－172(a＋b)的值．【例12】若a＋b＋c＝0，a3＋b3＋c3＝0，求证：a2011＋b2011＋c2011＝0．【练12】若a＋b－c＝3，a2＋b2＋c2＝3，那么a2012＋b2012＋c2012＝___________．【例13】(2009年北京市初二数学竞赛)设a＋b＋c＝0，a2＋b2＋c2＝1．(1)求ab＋bc＋ca的值；(2)求a4＋b4＋c4的值．【练13】若a＋b＋c＝1，a2＋b2＋c2＝2，a3＋b3＋c3＝83，(1)求abc的值；(2)求a4＋b4＋c4的值．巅峰突破【例14】若x＋y＝a＋b，且x2＋y2＝a2＋b2，求证:x2014＋y2014＝a2014＋b2014．【练14】已知a＋b＝c＋d，a3＋b3＝c3＋d3，求证:a2013＋b2013＝c2013＋d2013．【拓14】已知a＋b＝c＋d，a5＋b5＝c5＋d5，求证：a2013＋b2013＝c2013＋d2013．第8讲课后作业【习l】已知x2＋x－1＝0，求x8－7x4＋11的值．【习2】已知a＋b＋c＝1，b2＋c2－4ac＋6c＋1＝0，求abc的值．【习3】若m＝20062＋20062×20072＋20072，则m( )A．是完全平方数，还是奇数B．是完全平方数，还是偶数C．不是完全平方数，但是奇数D．不是完全平方数，但是偶数【习4】正整数a、b、c是等腰三角形三边的长，并且a＋bc＋b＋ca＝24，则这样的三角形有( ) A．1个B．2个C．3个D．4个【习5】已知a、b、c是一个三角形的三边，则a4＋b4＋c4－2a2b2－2b2c2－2c22a2的值( ) A．恒正B．恒负C．可正可负D．非负【习6】如果a＋2b＋3c＝12，且a2＋b2＋c2＝ab＋bc＋ca，求a＋b2＋c3的值．【习7】已知实数a、b、x、y满足a＋b＝x＋y＝2，ax＋by＝5，求(a2＋b2)xy＋ab(x2＋y2)的值．【习8】已知x是实数并且x3＋2x2＋2x＋1＝0．求x2008＋x2011＋x2014的值．【习9】(1999年北京市初二数学竞赛)若3x3－x＝1，求9x4＋12x3－3x2－7x＋2010的值．的值．【习11】(十八届希望杯初二二试)已知a1，a2，a3，…，a2007，是彼此互不相等的负数，且M＝(a1＋a2＋…＋a2006)(a2＋a3＋…＋a2007)，N＝(a1＋a2＋…＋a2007)(a2＋a3＋…＋a2006)，试比较M、N的大小．【习12】(2013年联赛)已知实数x，y，z满足x＋y＝4，|z＋1|＝xy＋2y－9，则x＋2y＋3z＝_______．【习13】(2013年竞赛)已知正整数a、b、c满足a＋b2－2c－2＝0，3a2－8b＋c＝0，则abc的最大值为____________．【习14】(2001年联赛)求实数x，y的值，使得(y－1)2＋(x＋y－3)2＋(2x＋y－6)2达到最小值．。

联赛题型解读（一）——整式与恒等变形左右。

而代数的基础便是整式,其中乘法公式、因式分解以及恒等变形,为代数提供了丰富的知识和技巧。

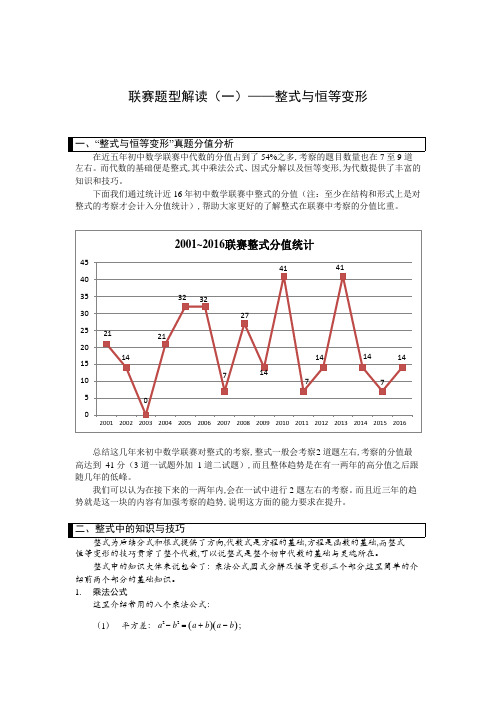
下面我们通过统计近16 年初中数学联赛中整式的分值（注：至少在结构和形式上是对整式的考察才会计入分值统计）,帮助大家更好的了解整式在联赛中考察的分值比重。

总结这几年来初中数学联赛对整式的考察,整式一般会考察2道题左右,考察的分值最高达到41 分（3 道一试题外加 1 道二试题）,而且整体趋势是在有一两年的高分值之后跟随几年的低峰。

我们可以认为在接下来的一两年内,会在一试中进行2 题左右的考察。

而且近三年的趋势就是这一块的内容有加强考察的趋势,说明这方面的能力要求在提升。

恒等变形的技巧贯穿了整个代数,可以说整式是整个初中代数的基础与灵魂所在。

整式中的知识大体来说包含了：乘法公式,因式分解及恒等变形,三个部分,这里简单的介绍前两个部分的基础知识。

1.乘法公式这里介绍常用的八个乘法公式：（1）平方差：a2 -b2 =(a +b)(a -b)；⎣⎦（2） 平方： (a ± b )2= a 2 ± 2ab + b 2 ；（3） 三元完全平方： (a + b + c )2= a 2 + b 2 + c 2 + 2ab + 2bc + 2ca ；（4）a 2 +b 2 +c 2 ± ab ± bc ± ca = 1 ⎡(a ± b )2 + (b ± c )2 + (c ± a )2⎤ ； 2 （5） 和（差）的立方： (a + b )3= a 3 + b 3 + 3ab (a + b );(a - b )3= a 3 - b 3 - 3ab (a - b )；（6） 立方和（差）： a 3 + b 3 = (a + b )(a 2 - ab + b 2 ); a 3 - b 3 = (a - b )(a 2 + ab + b 2 )；（7）（8） a 3 + b 3 + c 3 - 3abc = (a + b + c )(a 2 + b 2 + c 2 - ab - bc - ca )-a 4 - b 4 - c 4 + 2a 2b 2 + 2b 2c 2 + 2c 2 a 2= (a + b + c )(a + b - c )(b + c - a )(c + a - b )2. 因式分解简单的介绍一下初中阶段可以学习和使用的 10 种常见因式分解的方法： （1） 提取公因式：上午+下午=（上+下）午；（2） 公式法： x 6 - y 6 = (x 3 + y 3 )(x 3 - y 3 ) = (x + y )(x - y )(x 2 + xy + y 2 )(x 2 - xy + y 2 )； （3） 分组分解法： ax + ay + bx + by = a (x + y ) + b (x + y ) = (a + b )(x + y ) ； （4） 十字相乘:二次三项式 abx 2 + (ad + bc ) x + cd = (ax + b )(cx + d ) ；（5） 双十字相乘：选定两个二次三项式进行十字相乘；分步两次十字相乘大致相同； （6） 拆项天项: a 4 + a 2b 2 + b 4 = a 4 + 2a 2b 2 + b 4 - a 2b 2 = (a 2 + ab + b 2 )(a 2 - ab + b 2 ) ; （7） 整体换元：对于较复杂的式子可以进行适当换元让结构形式变得简单；（8） 主元法：多字母的代数式,可以选择结构较好的字母当做主元进行因式分解； （9） 因式定理：多项式 f (x ) ,当 x = a 的时候 f (a ) = 0 ,则 f ( x ) 有因式 x - a （10） 轮换对称式:简单举例：若关于 x 、y 、z 的轮换式有因式 x - y ,则其有因式(x - y )( y - z )(z - x )前 8 种因式分解的方法在初中均要求学生掌握,后 2 种有兴趣有精力的学生可以选择性的进行学习。

整式恒等变形【专题简介】把一个多项式在一个范围（如有理数范围内分解，即所有项均为有理数）化为几个最简整式的积的形式，这种变形叫做因式分解，也叫作分解因式，在数学求根作图方面有很广泛的应用．因式分解是代数式恒等变形的基础之一，方法众多，相应的训练对学生的代数能力提升较为明显．基本的分解方法有：①提公因式法②公式法③十字相乘常见分解技巧有：①主元法②换元法③拆添法④双十字相乘法高端分解方法有：①因式定理②待定系数③轮换对称【学习目标】学习换元法、因式定理、待定系数题型一消元与降次强化挑战【例1】化简(y＋z－2x)2＋(z＋x－2y)2＋(x＋y－2z)2－3(y－z)2－3(x－y)2－3(x－z)2【练1】已知x，y，z为有理数，(y－z)2＋(x－y)2＋(x－z)2＝(y＋z－2x)2＋(z＋x－2y)2＋(x＋y－2z)2，求(yz＋1)(zx＋1)(xy＋1)的值．()z2＋1x2＋1()y2＋1()【例2】（第14届希望杯1试）若x＋y＝－1，求x4＋5x3y＋x2y＋8x2y2＋xy2＋5xy3＋y4的值【练2】当x－y＝1，求x4－xy3－x3y－3x2y＋3xy2＋y4的值【例3】（第14届希望杯邀请赛试题）如果x2＋x－1＝0，那么x3＋2x2＋3＝.【练3】（1990年第一届希望杯初二第一试）已知3x2＋4x－7＝0，求6x4＋11x3－7x2－3x－7的值．题型二因式分解基础夯实【例3】（1）已知a5＋a4b－a4＋a－b－1＝0，且2a－3b＝1，则a3＋b3＝.(2)若a4＋b4＝a2－2a2b2＋b2＋6，则a2＋b2＝.(3)已知a ＞b ＞c ≥0，求适合等式abc ＋ab ＋bc ＋ac ＋a ＋b ＋c ＝2011的整数a 、b 、c 的值．【练4】（1）方程xy －2x －2y ＋7＝0的整数解（x ≤y ）为 .(2)若x 5＋x 4＋x ＝－1，则x ＋x 2＋x 3＋…＋x 2012＝ .(3)已知15x 2－47xy ＋28y 2＝0，求x y的值．【例5】长方形的周长为16cm ，它的两边x ，y 是整数，且满足x －y －x 2＋2xy －y 2＋2＝0，求它的面积．【练5】矩形的周长为28cm ，它的两边长x cm ，y cm ，且x 3＋x 2y －xy 2－y 3＝0，求矩形的面积．强化挑战【例6】（已知a 、b 、c 为三角形的三条边，且a 2＋4ac ＋3c 2－3ab －7bc ＋2b 2＝0，求2b ＝a ＋c .【练6】（1）在三角形ABC 中，a 2－16b 2－c 2＋6ab ＋10bc ＝0，其中a ，b ，c 是三角形的三边，求证：a ＋c ＝2b .(2)已知∆ABC 三边a ，b ，c 满足条件a 2c －a 2b ＋ab 2－b 2c ＋c 2b －ac 2＝0，试判断∆ABC 的形状，并说明理由．题型三乘法公式强化挑战【例7】若x ＋y ＝a ＋b ，且x 2＋y 2＝a 2＋b 2，求证：x 2014＋y 2014＝a 2014＋b 2014.【练7】已知a ＋b ＝c ＋d ，a 3＋b 3＝c 3＋d 3，求证：a 2013＋b 2013＝c 2013＋d 2013.巅峰突破【例8】已知a＋b＝c＋d，a5＋b5＝c5＋d5，求证：a2013＋b2013＝c2013＋d2013.【练8】（第6届希望杯初一）已知ax＋by＝7，ax2＋by2＝49，ax3＋by3＝133，ax4＋by4＝406，试求1995(x＋y)＋6xy－172(a＋b)的值【例9】已知a＋b＋c＝0，a3＋b3＋c3＝0，求证：a2011＋b2011＋c2011＝0. 【练9】若a＋b－c＝3，a2＋b2＋c2＝3，那么a2012＋b2012＋c2012＝．【例10】（2009北京市初二数学竞赛）设a＋b＋c＝0，a2＋b2＋c2＝1，（1）求ab＋bc＋ac的值（2）求a4＋b4＋c4的值【练10】若a＋b＋c＝0，a2＋b2＋c2＝1，a3＋b3＋c3＝83，求①abc的值；②a4＋b4＋c4的值题型四配方深入研究【例11】已知x2＋2xy＋2y2＋4y＋4＝0，求x，y【练11】已知x2－6xy＋10y2－4y＋4＝0，求x，y【例12】已知x2＋2xy＋2y2＋4x＋8＝0，求x，y【练12】已知x2－6xy＋10y2＋2x－8y＋2＝0，求x，y.【例13】已知实数a ，b ，c 满足a －b ＋c ＝7，ab ＋bc ＋b ＋c 2＋16＝0，则 b a的值等于 ．【练13】已知a －b ＝4，ab ＋c 2＋4＝0，则a ＋b ＝ ．【例14】当x 变化时，分式3x 2＋6x ＋512x 2＋x ＋1的最小值是 ．【练14】（2000年联赛）实数x ，y 满足x ≥y ≥1和2x 2－xy －5x ＋y ＋4＝0，则x ＋y＝ .第9讲7年级尖端班课后作业【习1】已知求x2＋x－1＝0，求x8－7x4＋11的值.【习2】已知a＋b＋c＝1，b2＋c2－4ac＋6c＋1＝0，求abc的值．【习3】若m＝20062＋20062×20072，则m（）A．是完全平方数还是奇数B.是完全平方数，还是偶数C．不是完全平方数，但是奇数D.不是完全平方数，但是偶数【习4】正整数a、b、c是等腰三角形三边的长，并且a＋bc＋b＋ca＝24则这样的三角形有（）A．1个B．2个C．3个D．4个【习5】已知a、b、c是三角形三边，则a4＋b4＋c4－2a2b2－2b2c2－2c2b2的值（）A恒正B恒负C可正可负D非负【习6】如果a＋2b＋3c＝12，且a2＋b2＋c2＝ab＋bc＋ca，求a＋b2＋c3的值【习7】已知实数a、b、x、y满足a＋2b＝x＋y＝2，ax＋by＝5，求（a2＋b2）xy＋ab（x2＋y2）的值【习8】已知x是实数，并且x3＋2x2＋2x＋1＝0，求x2008＋x2011＋x2014的值【习9】（1999年北京初二数学竞赛）若3 x3－x＝1，求9x4＋12x3－3x2－7x＋2010的值．【习10】（第18届希望杯初一）有理数a、b、c满足a∶b∶c＝2∶3∶5，且a2＋b2＋c2＝abc，求a＋b＋c的值．【习11】（2010北京市初二数学竞赛）x、y为实数，满足x＋y＝1，x4＋y4＝72，求x2＋y2的值．【习12】（十八届希望杯初二二试）已知a1、a2、a3……a2007是彼此互不相等的负数，且M＝（a1＋a2＋a3……＋a2006）（a2＋a3……＋a2007）N＝（a1＋a2＋a3……＋a2007）（a2＋a3……＋a2006）试比较M、N的大小【习13】（2013年联赛）已知实数x、y、z满足x＋y＝4，│z＋1│＝xy＋2y－9，则x＋2y＋3z＝．【习14】（2013年竞赛）已知正整数a、b、c满足a＋b2－2c－2＝0，3a2－8b＋c＝0则abc的最大值为．【习15】（2001年联赛）求实数x、y的值，便得（y－1）2＋（x＋y－3）2＋(2x＋y－6)2达到最小值．。

整式的恒等变形1. 乘法公式也叫作简乘公式，就是把一些特殊的多项式相乘的结果加以总结，直接应用。

公式中的每一个字母，一般可以表示数字、单项式、多项式，有的还可以推广到分式、根式。

公式的应用不仅可从左到右的顺用（乘法展开），还可以由右到左逆用（因式分解），还要记住一些重要的变形及其逆运算――除法等。

⒉ 基本公式就是最常用、最基础的公式，并且可以由此而推导出其他公式。

完全平方公式：()2222a b a ab b ±=±+，平方差公式：()()22a b a b a b +-=-． 立方和（差）公式：()()2233a b a ab b a b ±+=±．⒊ 公式的推广：①多项式平方公式：()22222222222a b c d a b c d ab ac ad bc bd cd +++=+++++++++即：多项式平方等于各项平方和加上每两项积的2倍。

②二项式定理：()3322333a b a a b ab b ±=+±()4432234464a b a a b a b ab b ±=±+±+()554322345510105a b a a b a b a b ab b ±=±+±+±…………注意观察右边展开式的项数、指数、系数、符号的规律 ③由平方差、立方和（差）公式引伸的公式()()322344a b a a b ab b a b +-+-=-()()43223455a b a a b a b ab b a b +-+-+=+()()5432234566a b a a b a b a b ab b a b +-+-+-=-…………注意观察左边第二个因式的项数、指数、系数、符号的规律 在正整数指数的条件下，可归纳如下：设n 为正整数()()2122232222122n n n n n n n a b a a b a b ab b a b -----+-+-+-=-()()2212222122121n n n n n n n a b a a b a b ab b a b ---+++-+--+=+类似地： ()()123221n n n n n n n a b a a b a b ab b a b ------+++++=-⒋ 公式的变形及其逆运算由()2222a b a ab b +=++得()2222a b a b ab +=+-由()()3322333333a b a a b ab b a b ab a b +=+++=+++得()()3333a b a b ab a b +=+-+ 由公式的推广③可知：当n 为正整数时 n n a b -能被a b -整除， 2121n n a b +++能被a b +整除，22n n a b -能被a b +及a b -整除。

七年级上册数学第二单元整式整式是数学中的重要概念，它在代数运算中起到了重要作用。

在七年级上册的数学课程中，我们将学习整式的相关知识。

本文将详细介绍七年级上册数学第二单元整式的概念、性质和基本运算。

同时，我们还将探讨整式在实际问题中的应用。

一、整式的概念整式是由常数和变量按照代数运算规则通过加减乘的组合而得到的代数表达式。

例如：3x²+5x-2就是一个整式。

其中，3、5、-2是常数，x²和x则是变量的n次幂。

整式通常有以下几种形式：1. 常数：如3、-5等；2. 变量：如x、y等；3. 同类项的和：如2x+3x，或者2x²+3x²等。

二、整式的性质整式具有一些重要的性质：1. 恒等性：整式的恒等性是指两个整式在定义域内的值总是相等。

例如，2x+x和3x就是恒等的。

2. 同类项：整式中具有相同变量的项称为同类项。

例如，在3x²+5x+2中，3x²和5x都是同类项。

3. 系数：整式中每一项都有一个系数，表示该项的权重或倍数。

在3x²+5x+2中，3、5和2分别是x²、x和常数项的系数。

三、整式的基本运算整式的基本运算包括加法、减法和乘法。

1. 加法：将同类项的系数相加，保留相同的变量和指数。

例如，(3x²+5x)+(2x²+3x)等于5x²+8x。

2. 减法：将同类项的系数相减，保留相同的变量和指数。

例如，(3x²+5x)-(2x²+3x)等于x²+2x。

3. 乘法：使用分配律将每一项相乘，然后将同类项合并。

例如，(2x+3)(x+4)等于2x²+11x+12。

四、整式的应用整式在实际问题中有广泛的应用。

例如，可以用整式来表示图形的面积和周长，解决各种几何问题；还可以用整式来表示物体的运动规律，解决物理问题；此外，整式也可以用来表示经济、统计等领域的数据关系。

整式恒等变形一、配方法 (1)二、降次 (6)三、整体思想 (8)四、其他 (8)一、 配方法1. （1985年全国初中数学联赛1试）设2-=a b ，2-=b c 222++---a b c ab bc ca 的值为_______．【难度】 ★★【解析】15 令222S a b c ab bc ca =++---，则2222222222S a b c ab bc ca =++---222()()()a b b c c a =-+-+- ((222224=+++30=．∴130152S =⨯=．即22215a b c ab bc ca ++---=．2. （1986年全国初中数学联赛1试）设a ，b ，c ，d 都是整数，且22m a b =+，22n c d =+，则mn 也可表示成两个整数的平方和，其形式是：mn =__________．【难度】 ★★【解析】22()()ac bd ad bc -++或填22()()ac bd ad bc ++- 2222()()mn a b c d =+⋅+ 22()()ac bd ad bc =++- 22()()ac bd ad bc =-++填出以上两种形式的任何一种都是正确的．3. （1992年全国初中数学联赛1试）若21310x x -+=，则44x x -+的个位数字是（ ） A ．1 B ．3 C ．5 D ．7 【难度】 ★★ 【解析】D 由21310x x -+=知0x ≠， 所以113x x -+=，222133167x x -+=-=， 4421672x x -+=-．从而4421672x x -+=-的个位数字为927-=． 故选D ．4. （1992年全国初中数学联赛1试）若a ，b 都是正实数，且1110a b a b--=+，则33b a a b ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭__________． 【难度】 ★★★【解析】∵1110a b a b --=+，即1b a a b -=，而b a a b +．∴33333b a b a b a b a a b a b a b a b ⎛⎫⎛⎫⎛⎫⎛⎫+=+-⋅+=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭5. （1994年全国初中数学联赛1试）设a ，b ，c 是不全相等的任意实数，若2x a bc =-，2y b ca =-，2z c ab =-，则x ，y ，z （ ）A ．都不小于0B ．都不大于0C ．至少有一个小于0D ．至少有一个大于0【难度】 ★★★【解析】D 很容易可以联想到这样的公式；2222222()()()()a b c ab bc ca a b b c c a ++---=-+-+-， 所以有：2222()2()x y z a b c ab bc ca ++=++--- 222()()()0a b b c c a =-+-+->，即0x y z ++>，故x ，y ，z 中至少有一个大于0． 故选D ．6. （1998年全国初中数学联赛1试）设a ，b 为实数，那么222a ab b a b ++--的最小值是_______． 【难度】 ★★★ 【解析】 1-222a ab b a b ++-- ()2212a b a b b =+-+-2213312424b a b b -⎛⎫=++-- ⎪⎝⎭()221311124b a b -⎛⎫=++--- ⎪⎝⎭≥ 当102b a -+=，10b -=， 即0a =，1b =时，上式不等式中等号成立，故所求最小值为1-．7. （1999年全国初中数学联赛1试）已知21()()()4b c a b c a -=--且0a ≠，则b ca+=__________． 【难度】 ★★★【解析】2 本题主要考查的是因式分解和一些常用的公式，首先反整个等式展开：∵()()()24b c a b c a -=--，即22224444b b c ac bc ab a -+=-+-， ∴22244420a b c ac ab bc ++--+=，很显然应该对上式逐步配方，然后即可得a b c ，，之间的关系： ∴()()22440b c a b c a +-++=， ∴()220a b c -+=⎡⎤⎣⎦， ∴2a b c =+， ∴2b ca+=．8. （2000年全国初中数学联赛1试）实数x ，y 满足1x y ≥≥和22540x xy x y --++=，则x y +=________．【难度】 ★★★【解析】4 解法一：对于二元的方程，要求未知数我们一般考虑方程的判别式，但对于本题来说，我们应该利用条件所给的不等式，通过配方来分析．2254x xy x y --++()()2244x x x xy x y =-++--+()()()221x x y x =-+--0=．又0x y -≥，1x -≥0，()220x -≥，所以()()()2210x x y x -=--=． 故2x y ==，4x y +=． 解法二：由已知条件条形得()()225411x x y x x x -+=--≤，即2440x x -+≤．()2202x x -⇒=≤．代回原式得到2y =． 得4x y +=．9. （2001年全国初中数学联赛2试）在直角坐标系中有三点(01)A ，，(13)B ，，(26)C ，；已知直线y ax b =+上横坐标为0，1，2的点分别为D ，E ，F ．试求a ，b 的值使得222AD BE CF ++达到最小值．【难度】 ★★★【解析】 D ，E ，F 的坐标为()0D b ，，()1E a b +，，()22F a b +，， 由图象可知：()()()2222221326AD BE CF b a b a b ++=-++-++-22563302046a ab b a b =++--- ()2563032046a b a b b 2=+-+-+2236532155a b b b ⎛⎫=+-+-+ ⎪⎝⎭223651535566a b b ⎛⎫⎛⎫=+-+-+ ⎪ ⎪⎝⎭⎝⎭，当3305506a b b ⎧+-=⎪⎪⎨⎪-=⎪⎩时，上式取得最小值，此时52a =，56b =，最小值为16．10. （2001年全国初中数学联赛2试）求实数x ，y 的值，使得222(1)(3)(26)y x y x y -++-++-达到最小值．【难度】 ★★★【解析】 ()()()2221326y x y x y -++-++-22563302046x xy y x y =++--+()2563032046x y x y y 2=+-+-+2223353533204655x y y y y ⎛⎫⎛⎫=+---+++ ⎪ ⎪⎝⎭⎝⎭2236532155x y y y ⎛⎫=+-+-+ ⎪⎝⎭223651535566x y y ⎛⎫⎛⎫=+-+-+ ⎪ ⎪⎝⎭⎝⎭当3305506x y x ⎧+-=⎪⎪⎨⎪-=⎪⎩时，上式取得最小值，此时52x =，56y =，最小值为16．11. （1995年全国初中数学联赛1试）设x 为正实数，则函数21y x x x=-+的最小值是_________．【难度】 ★★【解析】1， 这个题目是将二次函数2y x x =-与反比例函数1y x=作叠加，前面已经说过要求极值一般情况下是要配方的，这里出现了1x，可以联想到公式212x x +-=，这样我们进行两次配方可得：()()22211111y x x x x =-++-=-++． 因而1x =时，y 有最小值1．12. （2013年全国初中数学联赛1试）已知实数x ，y ，z 满足4x y +=，|1|29z xy y +=+-，则23x y z ++=________． 【难度】 ★★【解析】4 由题意：4x y =-，∴()()22|1|29429693z xy y y y y y y y +=+-=-+-=-+-=--， ∴310y z -=+=，∴131x y z ===-，，，∴234x y z ++=．13. （2013年全国初中数学联赛2试）已知实数a b c d ，，，满足222222323()6a c b d ad bc +=+=-=，求2222()()a b c d ++的值．【难度】 ★★★★【解析】 设22m a b =+，22n c d =+，则222223223312m n a b c d +=+++=．因为22(23)(23)2424m n m n mn mn +=-+≥，即21224mn ≥，所以6mn ≤① 又因为222222222222()()mn a b c d a c b d a d b c =++=+++222()()()6ac bd ad bc ad bc =++--=≥② 由①，②可得6mn =，即2222()()6a b c d ++=．注：符合条件的实数a b c d ，，，存在且不唯一，a 1b =，c =，d =14. （2013年全国初中数学联赛1试）如果实数x ，y ，z 满足222()8x y z xy yz zx ++-++=，用A 表示||x y -，||y z -，||z x -的最大值，则A 的最大值为________．【难度】 ★★★不妨设x y z >>，则A x z =-，令x y a -=，y z b -=，则x z a b -=+，由222()8x y z xy yz zx ++-++=可知，()()()222182x y y z z x ⎡⎤-+-+-=⎣⎦， ∴()22216a b a b +++=，228a b ab ++=，∵()2223830a b a b ab ab ab -=++-=-≥，∴83ab ≤，∴()2832833a b ++=≤，∴a b +．二、 降次15. （1994年全国初中数学联赛1试）当x =32001(419971994)x x --的值为（ ） A ．1B ．1-C ．20012D ．20012-【难度】 ★★【解析】B因为x ()2211994x -=，即24419930x x --=． 于是，()20013419971994x x --()()2001224419934419931x x x x x ⎡⎤=--+---⎣⎦()200111=-=-．故选B ．16. （1986年全国初中数学联赛1试1试）若x =，则分式4322621823815x x x x x x --++=-+_________． 【难度】 ★★【解析】5 ∵4x ==∴28130x x -+=．且分式的分母除以2813x x -+后余2，分式的分子除以2813x x -+后余10． ∴原式值为5．17. （1995年全国初中数学联赛1试1试）已知a 是方程2104x x +-=的根，则354321a a a a a -+--的值等于_______．【难度】 ★★【解析】20这类问题一般都先化简后代值，直接把a =代入将导致复杂的计算． 由已知，有214a a +=，① 原式()()()()2221111a a a a a a -++=-+ ()()222211142014a a a a +++===⎛⎫+ ⎪⎝⎭． 同学们在这道题上的错误主要是化简的方向不明确，最后又不会将2a a +作为整体代入．这里关键是整体代入，抓住这一点，计算可以灵活．由①有3214a a a +=，②54314a a a +=③由②-①，得 ()3114a a a -=-④由③-②并将④代入，得()()54323111416a a a a a a a +--=-=-．⑤ ()()32111611612014116a a a a -⎛⎫==++=+= ⎪⎝⎭-原式18. （2008年全国初中数学联赛1试）设a ，则5432322a a a a a a a+---+=-________．【难度】 ★★ 【解析】 2-∵221a a ==-⎝⎭，∴21a a +=，∴()()32325432322222a a a a a a a a a a a a a a a a+--+++---+=-⋅- ()()333322212111(11)211a a a a a a a a a a a --+--===-=-++=-+=-⋅----．19. （2009年全国初中数学联赛1试）设1a ，则32312612a a a +--=（ ） A ．24B ．25 C．10 D．12【难度】 ★★ 【解析】A 由()217a +=，有2226,62a a a a +==-．于是32312612a a a +--()()3621262612a a a a =-+---()2261212621224a a a a =+-=+-=三、 整体思想四、 其他20. （1996年全国初中数学联赛1试）设333199519961997x y z ==，0xyz >，且，则111x y z++=________．【难度】 ★★★ 【解析】1 设333199519961997x y z k ===，显然0k ≠，所以： 333199519961997k k kx y z ===，，，带入方程可得：333=．即：33111x y z ⎛⎫++ ⎪⎝⎭． ∵0k ≠，∴111x y z=++． 由已知可得0x >，0y >，0z >， ∴1111x y z++=.21. （1997年全国初中数学联赛1试）若实数a ，b ，c 满足2229a b c ++=，代数式222()()()a b b c c a -+-+-的最大值是（ ） A ．27B ．18C ．15D ．12【难度】 ★★ 【解析】A ()()()()()22222222a b b c c a a b c ab bc ca -+-+-=++-++，考虑到等式()()22222a b c a b c ab bc ca ++=+++++， 将两个等式相加得到()()()()()2222222327a b b c c a a b c a b c -+-+-+++=++=，当0a b c ++=时，()()()222a b b c c a -+-+-有最大值27． 故选A ．22. （2002年全国初中数学联赛1试）若22m n =+，22()n m m n =+≠，则332m mn n -+的值为（ ） A ．1 B ．0C ．1-D ．2-【难度】 ★★ 【解析】D22m n =+，22n m =+，两式相减得到()()2210m n n m m n m n -=-⇒-++=．又m n ≠，所以1m n +=-，由立方和公式()()332222m mn n m n m mn n mn -+=+-+- ()222m mn n mn =--+-22m mn n =---()2m m n n =-+-2m n =-．又由已知条件22n m =+，所以33222m mn n m n -+=-=-，故选择D ．23. （2004年全国初中数学联赛1试）已知0abc ≠，且0a b c ++=，则代数式222a b c bc ca ab++的值是（ ） A ．3 B ．2 C ．1 D ．0【难度】 ★★【解析】A 本题利用基本恒等式来变形： 原代数式222333a b c a b c bc ca ab abc++++=． 又()()3332223a b c a b c a b c ab bc ca abc ++=++++---+． 由已知0a b c ++=，故33330a b c abc ++-=．即3333a b c abc ++=，代回原式得到2223333a b c a b c bc ca ab abc++++==，选A ．24. （2012全国初中数学联赛1试）已知实数a b ，满足221a b +=，则44a ab b ++的最小值为（ ） A ．18- B ．0 C ．1 D ．98 【难度】 ★★★【解析】B ()()22244222219221248a ab b a b a b ab ab ab ab ⎛⎫++=+-+=-++=--+ ⎪⎝⎭， 又∵()20a b +≥，()20a b -≥，故1122ab -≤≤， ∴当12ab =-时，44a ab b ++取最小值0．。