solidworks方程式草图
- 格式:doc
- 大小:2.68 MB
- 文档页数:9




SolidWorks方程式的使用
SolidWorks方程式的使用
在SolidWorks中,方程式的使用必不可少,因为很多时候我们的模型可能是根据其他模型变过来的或者和其他模型存在某种关系,这个时候方程式就派上用场了,那么方程式能做什么呢?方程式其实和Excel基本类似,下面我们就看一下吧。
1. 打开SolidWorks绘制出相关产品模型,完善产品基本数据。
1. 2. 在设计树内找到方程式点击右键进入管理方程式或者工具—【∑方程式】
1. 3. 在方程式内找到需要使用条件的尺寸
1. 4. 键入你需要的条件,例:如果草图1的尺寸小于65,那么螺栓长度为100,否则为120(D1@凸台-拉伸=IIF(”D1@草图1”<65,”100”,”120”))
1. 5.如果D1@草图1=60,相对应的螺栓长度就应该为100
上述是if语句,其实在SolidWorks 方程式里面还能进行方程式讲特征压缩:
我们也可以通过用if语句的方式给特征进行条件压缩/解压缩,当然有人要问了这个压缩和在设计树里压缩有什么不同,可以告诉你肯定是不同的,首先是有条件给他压缩,切条件在,在设计树里就不能进行解除压缩。
大家可以试验一下。
SolidWorks不仅支持条件语句还提供更多的选择,如三角函数等,大家都可以根据自己的需要来选择,能让设计者能更方便和快捷的来设计。





SolidWorks中“方程式驱动的曲线”工具的应用潘思达SolidWords自从2007版开始,草图绘制工具中添加了“方程式驱动的曲线”工具,用户可通过定义”笛卡尔坐标系”(暂时还不支持其他坐标系) 下的方程式来生成你所需要的连续曲线。
这种方法可以帮助用户设计生成所需要的精确的数学曲线图形,目前可以定义“显式的”和“参数的”两种方程式。
本文将分别依次介绍这两种方程式的定义方法,以及绘制一些特殊曲线时的注意事项。
“显式方程”在定义了起点和终点处的 X 值以后,Y 值会随着 X 值的范围而自动得出;而“参数方程”则需要定义曲线起点和终点处对应的参数(T)值范围,X 值表达式中含有变量 T,同时为Y值定义另一个含有T值的表达式,这两个方程式都会在T的定义域范围内求解,从而生成需要的曲线。
下面介绍一下笛卡尔坐标系下常用的一些曲线的定义方法,通过图片可以看出所绘制曲线的关键位置的数值。
对于有些在其他坐标系下定义的曲线方程,例如极坐标系方程,大家可以使用基本的数学方法先将该坐标系下的曲线方程转化到笛卡尔坐标系以后就可以重新定义该曲线了。
关于“方程式曲线”对话框其他的选项功能大家可以参照SolidWords帮助文件详细了解使用方法。
(一)显式方程类型:正弦函数函数解析式:1正弦曲线是一条波浪线,k、ω和φ是常数(k、ω、φ∈R,ω≠0)2A——振幅、(ωx+φ)——相位、φ——初相3k——偏距、反应图像沿Y轴整体的偏移量4ω目标:模拟交流电的瞬时电压值得正玄曲线图像,周期,φ=,A=2操作:新建零件文件→工具→选择绘图基准面→方程式驱动的曲线,键入如下方程。
方程式:X1=- ,X2=函数图像:如图 1-1 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-1类型:一次函数函数解析式:Yx=1一次函数是一条直线 , y值与对应x值成正比例变化,比值为k 2k、b是常数,x∈R目标:模拟速度—位置曲线,k=4,b=0操作:新建零件文件→选择基准面→驱动的曲线,键入如下方程方程式: Yx=4*x+0函数图像:如图 1-2 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-2类型:二次函数函数解析式:Yx=1平面内,到一个定点F和不过F的一条定直线L距离相等的点的轨迹(或集合)称之为抛物线。
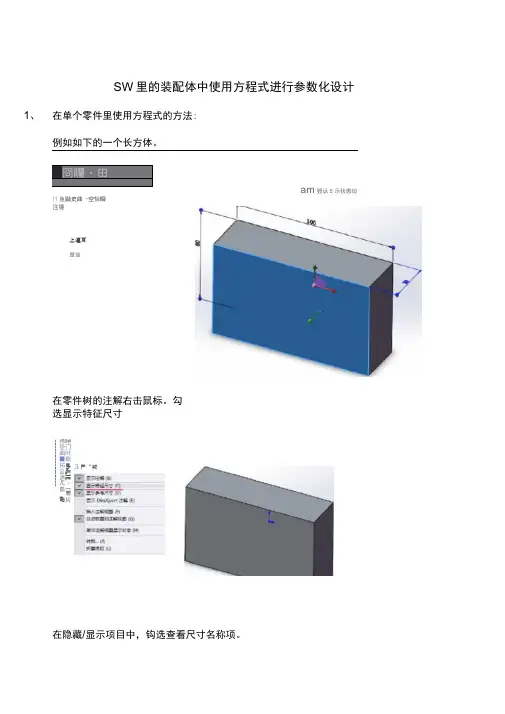
SW 里的装配体中使用方程式进行参数化设计在单个零件里使用方程式的方法:例如如下的一个长方体。
冏矚・田am 毀认5示状恚垃!1鱼鼬史曲 -空怡瞬 注境在零件树的注解右击鼠标。
勾选显示特征尺寸在隐藏/显示项目中,钩选查看尺寸名称项。
1、 上連耳 厚音睜门叶菇mhJLIE -『Ml 片務箜曲■祐0&遗儿血 曲----------------3尸“戒也可以在视图菜单中选择显示尺寸名称0 規囹、询措入咼工畀曰 Sinul^tian Toorbgx Phot^View 560 妾匚旳稱E添加方程式。
菜单下拉“工具”二》“方程式”,打开方程式对话框。
S 一oil 一一Ctrl +R昱示(D)*悸險【林〕光源与柜机(口 >基准邮 活曲」垢面⑴BmafX)』蔦点(I) 呈标至(0 草图⑸ 网梧⑹^(N)步蹈点血这样只要我们点中零件。
零件就会显示出尺寸及其名称了闵 ■一a -m «-・n ^B ・・!r ^!-!----J J方程式 垒本吏量、及尺寸然后在对应的列里,点选零件显示的尺寸名称即可在方程式对话框中。
点击“按序排列视图”名称D2£罩多-"—便的画]数值/方程式无论是草图尺寸还是特征。
都可以互相进行方程式。
2、 下面在装配体中进行方程式的添加。
新建立2个零件。
曹f仔—0]佻 --------------- ■ I Wvi W]] 5i*nJBtifln |・张• B 4"用式.牛注用尺岂E T 民协P 霄西碎眉吟snIfiAH 1亠「•" T ~-~一Hmm-D?a<ril三琲mJ然后新建装配体。
把这2个零件装配起来。
在注解里勾上显示特征尺寸视图菜单里把尺寸名称显示这样只要双击装配体中的零件,就会显示出尺寸及名称。
方便我们添加方程式。
开始在装配体中添加方程式。
比如我们要零件3的宽度二零件4的长度的一半。
方程式如下:JOO£回M 才坤冏吟承椁-Krta/加m5酝_ >奸>名称处点选零件3的D1尺寸。

SolidWorks3D—草图和方程式驱动曲线的练习
'
此图用SolidWorks2019版建模,用KeyShot 9.0 渲染(上面两
张图)。
SW原文件在今日文件夹里。
建模过程
1.在【前视基准面】上画一个内切圆三角形。
(多边形)
2.【曲面拉伸】两侧对称:30 。
3.进入【3D草图】在各条边线的中点上画一个:点。
4.【通过参考的的曲线】依次点选上一步画的草图点,闭环曲线打勾。
5.【删除/保留实体】删除蓝色面。
6.【扫描】圆形轮廓,直径:10 。
(圆形轮廓,2016版才开始有这个功能)
7.添加外观。
也可以用方程式画一个类似的图形
8.进入【3D草图】——在样条曲线的下拉菜单里选择【方程式驱动的曲线】。
8-1.输入方程式:
Xt=sin(t)+2*sin(2*t) Yt=cos(t)-2*cos(2*t) Zt=sin(3*t)
t1=0 ; t2=1.995*pi
9.【扫描】圆形轮廓,直径:1 。
10.可以把图形整体调大一些,修改方程如下:
11.轮廓直径改为:10 。
12.完成。
13.用KeyShot简单渲染一下:
'。
第2章绘制草图2.3 上机指导SolidWorks是一个尺寸驱动式的绘图软件,因此绘图的方式和以前传统的绘图方式有很大的不同。
在绘制草图的过程中应该注意以下几个原则。
根据建立特征的不同以及特征间的相互关系,确定草图的绘图平面和基本形状。
零件的第一幅草图应该以原点定位,从而确定特征在空间的位置。
每一幅草图应尽量简单,不要包含复杂的嵌套,有利于草图的管理和特征的修改。
2.3.1 中心线、直线练习绘制如图2.9所示草图。
图2.9 中心线、直线练习(1)(2)(3) 2.10所示。
图2.10 绘制水平中心线提示:在绘制草图时,中心线非常重要,尤其对于形状对称的图形,利用中心线和镜向命令,能提高作图效率和准确性。
中心线还可用来给图元(即图形元素)定位和标注尺第2章 绘制草图·11··11· 寸,但不会影响零件特征的创建。
(4)2.11所示。
图2.11 绘制直线 (5)2.9所示。
(6) 2.3.2 圆中心线、圆、圆角练习绘制如图2.12(1)(2)(3)3条互成120°B 和C ,单击【圆】按185圆DD ,如图 2.13 所示。
图2.12 圆中心线、圆、圆角练习 图2.13 圆转化为构造几何线(4)E 、F 、G 、H 、I 、J 、K 和L 。
单击【添加几何关系】E 、F 和G;再次单J ,建立“相等”几何关系,单击【确定】按钮2.14所示。
(5) 3个凸缘,如图2.15所示。
SolidWorks 2007基础教程与上机指导·12· ·12·图2.14 圆图2.15 修整3个凸缘 (6)输入“10mm2.12所示。
(7)2.3.3 草图综合练习绘制如图2.16所示草图。
图2.16 综合练习草图效果(1)(2)(3)尺寸。
如图2.17(4)A 、B 和C 45第2章 绘制草图·13· ·13·圆BD ,标注尺寸,如图2.18所示。
在SolidWorks中,可以使用3D草图和方程式驱动的曲线来创建基于方程式的3D曲线。
具体步骤如下:
打开SolidWorks并进入3D建模模式。
在功能树中选择“草图”选项,然后选择“方程式驱动的曲线”。
在方程式输入框中输入您想要的曲线方程。
例如,要创建一个半径为r的圆,可以使用方程式x=cos(t)*r、y=sin(t)*r、z=0,其中t是参数,x、y、z是曲线上点的坐标。
根据需要设置其他参数,如曲线的起始点和结束点。
点击“确定”按钮,SolidWorks将根据您输入的方程式生成相应的3D曲线。
通过这种方式,您可以使用SolidWorks创建各种基于方程式的3D曲线,如螺旋线、摆线、椭圆等。
这些曲线可用于创建复杂的3D模型,并在需要精确几何形状的应用中使用。
SolidWorks 中“方程式驱动的曲线”工具的应用潘思达SolidWords 自从2007版开始,草图绘制工具中添加了“方程式驱动的曲线”工具,用户可通过定义”笛卡尔坐标系”(暂时还不支持其他坐标系) 下的方程式来生成你所需要的连续曲线。
这种方法可以帮助用户设计生成所需要的精确的数学曲线图形,目前可以定义“显式的”和“参数的”两种方程式。
本文将分别依次介绍这两种方程式的定义方法,以及绘制一些特殊曲线时的注意事项。
“显式方程”在定义了起点和终点处的 X 值以后,Y 值会随着 X 值的范围而自动得出;而“参数方程”则需要定义曲线起点和终点处对应的参数(T)值范围,X 值表达式中含有变量 T ,同时为Y 值定义另一个含有T 值的表达式,这两个方程式都会在T 的定义域范围内求解,从而生成需要的曲线。
下面介绍一下笛卡尔坐标系下常用的一些曲线的定义方法,通过图片可以看出所绘制曲线的关键位置的数值。
对于有些在其他坐标系下定义的曲线方程,例如极坐标系方程,大家可以使用基本的数学方法先将该坐标系下的曲线方程转化到笛卡尔坐标系以后就可以重新定义该曲线了。
关于“方程式曲线”对话框其他的选项功能大家可以参照SolidWords 帮助文件详细了解使用方法。
(一)显式方程类 型: 正弦函数函数解析式:Yx=A ×si n(ωx +φ)+k 1正弦曲线是一条波浪线,k 、ω和φ是常数(k 、ω、φ∈R ,ω≠0) 2A ——振幅、(ωx+φ)——相位、φ——初相 3k ——偏距、反应图像沿Y 轴整体的偏移量 4 ω=2πT目 标:模拟交流电的瞬时电压值得正玄曲线图像,周期T=2π3,φ=π2,A=2 操 作:新建零件文件→工具→选择绘图基准面→方程式驱动的曲线,键入如 下方程。
方 程 式:Yx =2∗sin(3∗x +pi 2)X 1=- pi 2,X 2=pi 2函数图像:如图 1-1 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-1类型:一次函数函数解析式:Yx=kx+b1一次函数是一条直线 , y值与对应x值成正比例变化,比值为k2k、b是常数,x∈R目标:模拟速度—位置曲线,k=4,b=0操作:新建零件文件→选择基准面→驱动的曲线,键入如下方程方程式: Yx=4*x+0函数图像:如图 1-2 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-2类型:二次函数函数解析式:Yx=ax2+bx+c1平面内,到一个定点F和不过F的一条定直线L距离相等的点的轨迹(或集合)称之为抛物线。
SolidWorks中“方程式驱动的曲线”工具的应用
潘思达SolidWords自从2007版开始,草图绘制工具中添加了“方程式驱动的曲线”工具,用户可通过定义”笛卡尔坐标系”(暂时还不支持其他坐标系) 下的方程式来生成你所需要的连续曲线。
这种方法可以帮助用户设计生成所需要的精确的数学曲线图形,目前可以定义“显式的”和“参数的”两种方程式。
本文将分别依次介绍这两种方程式的定义方法,以及绘制一些特殊曲线时的注意事项。
“显式方程”在定义了起点和终点处的X 值以后,Y 值会随着X 值的范围而自动得出;而“参数方程”则需要定义曲线起点和终点处对应的参数(T)值范围,X值表达式中含有变量T,同时为Y值定义另一个含有T值的表达式,这两个方程式都会在T的定义域范围内求解,从而生成需要的曲线。
下面介绍一下笛卡尔坐标系下常用的一些曲线的定义方法,通过图片可以看出所绘制曲线的关键位置的数值。
对于有些在其他坐标系下定义的曲线方程,例如极坐标系方程,大家可以使用基本的数学方法先将该坐标系下的曲线方程转化到笛卡尔坐标系以后就可以重新定义该曲线了。
关于“方程式曲线”对话框其他的选项功能大家可以参照SolidWords帮助文件详细了解使用方法。
(一)显式方程
类型:正弦函数
函数解析式:
1正弦曲线是一条波浪线,k、ω和φ是常数(k、ω、φ∈R,ω≠0)
2A——振幅、(ωx+φ)——相位、φ——初相
3k——偏距、反应图像沿Y轴整体的偏移量
4ω
目标:模拟交流电的瞬时电压值得正玄曲线图像,周期,φ=,A=2
操作:新建零件文件?工具?选择绘图基准面?方程式驱动的曲线,键入如下方程。
方程式:
X1=- ,X2=
函数图像:如图1-1 所示,使用尺寸标注工具得出图像关键点对应的数值
图1-1
类型:一次函数
函数解析式:Yx=
1一次函数是一条直线, y值与对应x值成正比例变化,比值为k 2k、b是常数,x∈R
目标:模拟速度—位置曲线,k=4,b=0
操作:新建零件文件?选择基准面?驱动的曲线,键入如下方程
方程式: Yx=4*x+0
函数图像:如图1-2 所示,使用尺寸标注工具得出图像关键点对应的数值
图1-2
类型:二次函数
函数解析式:Yx=
1平面内,到一个定点F和不过F的一条定直线L距离相等的点的轨迹(或集合)称之为抛物线。
目标:模拟任意一条抛物线,a=、b=4、c=5
操作:新建零件文件--草图工具--选择基准面---方程式驱动的曲线,键入如下方程。
方程式: Yx=
X0=-5, X1=3
函数图像:如图1-3 所示,使用尺寸标注工具得出图像关键点对应的数值
图1-3
(二)参数方程
类型:阿基米德螺线
函数解析式:
1.阿基米德螺线亦称“等速螺线”,当一点P沿动射线OP以等速率运动的同时,
这射线又以等角速度绕点O旋转,点P的轨迹称为“阿基米德螺线”。
2.笛卡尔坐标方程式为:
3.将r带入方程整理后在SolidWorks中表示为:
t代表螺旋圈数、v理解为P点在射线OP上的直线速率
目标:
1.模拟基本的阿基米德螺线
2.试图将螺旋线起点开始的角度值修改为,即从Y轴开始螺旋
3.v=10
操作:新建零件文件--草图工具--方程式驱动的曲线--选择绘图基准面--点选“参数式”,键入如下方程。
目标方程式:
1.
函数图像1:如图1-4 所示,使用尺寸标注工具得出图像关键点对应的数值
图1-4
2.通过三角函数诱导公式进一步推倒得到以下结果,红色位置代表曲线绕原点的旋
转弧度值。
这里取值为pi/2
Xt= cos(pi/2)*10*(1+t)*cos(t*2*pi)-sin(pi/2)*10*(1+t)*sin(t*2*pi)
Yt= sin(pi/2)*10*(1+t)*cos(t*2*pi)+cos(pi/2)*10*(1+t)*sin(t*2*pi)
函数图像2:如图1-5所示,曲线起始点已与Y轴重合
图1-5
类型:渐开线
函数解析式:
将一个圆轴固定在一个平面上轴上缠线,拉紧一个线头,让该线绕圆轴运动且始终与圆轴相切,那么线上一个定点在该平面上的轨迹就是渐开线。
渐开线方程为:
X
Z=0
式中r为基圆半径;为展角其单位为弧度,在SolidWorks中可以表示为:
t代表展角范围
目标:模拟渐开线,展角0,r
操作:新建零件文件--草图工具--方程式曲线--选择基准面、点选“参数性”
方程式:
t0=0,t1=2*pi
函数图像:如图1-6所示
图1-6
类型:螺旋线
函数解析式:
SolidWorks软件在曲线工具栏中包含了既有的“螺旋线”工具,可以帮助用户完成变化多样的螺旋曲线,比如变半径、变螺距、锥形螺旋和平面螺旋等几种螺旋线。
下面使用“方程式曲线”工具来绘制最简单的一条螺旋线,螺旋半径和螺距都为恒定值。
方程式表示为:
式中R代表螺旋半径、P代表螺距、H代表曲线起始点距离原点的高度、t代表螺旋圈数可输入小数值。
目标:模拟一条螺旋线,R=20、P=10、H=5、t=5
操作:新建零件文件--草图工具--选择基准面---方程式驱动的曲线,键入如下方程。
t0=0, t1=5
函数图像:如图1-7 所示
图1-7
类型:圆周曲线
函数解析:
到平面内点P(a,b)距离等于定值R的点的集合就叫做叫做圆。
圆曲线方程为:
式中R为圆半径;点P(a,b)为圆心坐标,若a=b=0,在SolidWorks中可以表示为:
t代表射线OP与X轴夹角
目标:模拟3/4圆周曲线,0,r
操作:新建零件文件--草图工具--方程式曲线--选择基准面、点选“参数性”
方程式:
t0=0,t1=
函数图像1:如图1-8
图1-8
因为曲线方程工具暂时不支持封闭的曲线,即变量值起点与终点重合的情况,所以如果需要得到整个圆周曲线的话,可以先绘制半圆再进行镜像操作,如图1-9所示。
类似情况还有“星形曲线”、“叶形曲线”等等封闭曲线,如图1-10和1-11所示。
图1-9
图1-10
图1-11
通过上面的实例可以看出对于一般的方程式曲线,SolidWorks曲线方程式工具都可以很好的支持,相比以往通过绘制关键点坐标等等的其他方法来说,在曲线精度、绘制效率和修改参数等方面都极大地方便了用户。
如果绘制的曲线是封闭的且具有一定的对称性,那么在定义变量t的区间时可以先取整体的若干部分,镜像后即可。