有限元分析基础复习题

1. 数学:偏微分方程变换成代数方程进行求解2. 力学:连续体划分成小单元体,各单元节点间相连接并建立力平衡关系.3. 有限元模型:有限元模型是真实系统理想化的数学抽象.由一些简单形状的单元组成,单元之间通过节点连接,并承受一定载荷.4. 有限元法:是以力学理论为基础,随着力学\数学和计算机科学相结合而发展起来的一种数值计算方法.5. 传统结构设计流程:设计----建模----测试---再设计.(1)作很大简化,计算精度差;(2)结构尺寸与重量偏大;(3)结构局部强度或刚度不足;(4)设计周期长,试制费用高6. 现代产品设计: Design(CAD)----VirtualTest(CAE)---Build---Test---Redesign。

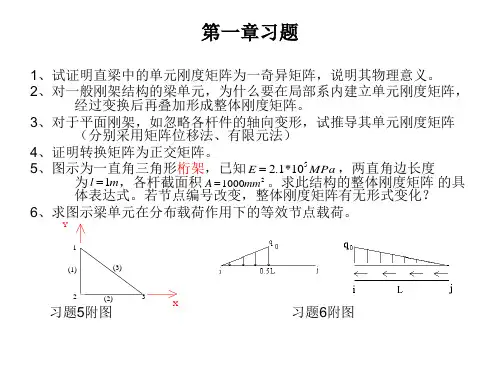
有限元法是CAE 的核心部分7. 汽车结构有限元分析的内容：（1）零部件及整车的疲劳分析，估计产品的寿命，分析部件损坏的原因；（2）结构件、零部件的强度、刚度和稳定性分析（3）结构件模态分析、瞬态分析、谐响应分析和响应谱分析；（4）车身内的声学设计，车身结构模态与车身内声模态耦合；（5）汽车碰撞历程仿真和乘员安全保护分析（被动安全性）；（6）结构件、零部件的优化设计（质量或体积为目标函数）；（7）车身空气动力学计算，解决高速行驶中的升力、阻力和湍流问题8. 汽车结构有限元分析的流程：（1）制定方案；（2）建立结构模型；（3）划分有限元模型；（4）有限元模型检查；（5）加载和增加约束条件；（6）求解计算；（7）结果分析。

P99. 模态分析：固有频率和振型，从数学上讲，固有频率就是系统矩阵的特征值，振型就是该特征值所对应的特征向量。

10.谐响应分析：确定结构对已知幅值和频率的正弦载荷的响应。

11.瞬态动力学分析：确定结构对随时间变化载荷的响应。

12.单元：用于离散结构的杆、梁、三角形、四边形、四面体、六面体等。

节点：单元与单元之间的连接点。

具有一定自由度和存在相互物理作用。

1、有限元法是近似求解（连续）场问题的数值方法。

2、有限元法将连续的求解域（离散），得到有限个单元，单元与单元之间用（节点）相连。

3、从选择未知量的角度看，有限元法可分为三类（位移法力法混合法）。

4、以（节点位移）为基本未知量的求解方法称为位移量。

5、以（节点力）为基本未知量的求解方法称为力法。

7、直梁在外力作用下，横截面上的内力有（剪力）和（弯矩）两个。

8、平面刚架结构在外力作用下，横截面上的内力有（剪力）、（弯矩）、（轴力）。

9、进行直梁有限元分析，节点位移有（转角）、（挠度）。

10、平面刚架有限元分析，节点位移有（转角）、（挠度）、（？？？）。

11、在弹性和小变形下，节点力和节点位移关系是（）。

12、弹性力学问题的方程个数有（15）个，未知量个数有(15)个。

13、弹性力学平面问题方程个数有（8），未知数（8）个。

15h、几何方程是研究（应变）和（位移）关系的方程。

16、物理方程描述（应力）和（应变）关系的方程。

17、平衡方程反映（应力）和（位移）关系的方程。

18、把进过物体内任意一点各个（截面）上的应力状况叫做（该点）的应力状态。

19、形函数在单元节点上的值，具有本点为（1），他点为零的性质，并在三角形单元的后一节点上，三个形函数之和为（1）。

20、形函数是（三角形）单元内部坐标的（线性位移）函数，它反映了单元的（位移）状态。

21、节点编号时，同一单元相邻节点的（编号）尽量小。

25、单元刚度矩阵描述了（节点力）和（节点位移）之间的关系。

矩形单元边界上位移是（线性）变化的。

从选择未知量的角度来看，有限元法可分为三类，下面那种方法不属于其中（C）。

力法B、位移法C、应变法D、混合法下面对有限元法特点的叙述中，哪种说法是错误的（D）。

可以模拟各种几何形状负责的结构，得出其近似值。

解题步骤可以系统化，标准化。

容易处理非均匀连续介质，可以求解非线性问题。

需要适用于整个结构的插值函数。

几何方程研究的是（A）之间关系的方程式。

《有限元法》复习题一. 单选题1.平面刚架单元坐标转换矩阵的阶数为（ ） A ．2⨯2 B ．2⨯4 C ．4⨯4 D ．6⨯62.图示的四根杆组成的平面刚架结构，用杆单元进行有限元分析，单元和节点的划分如图示，则总体刚度矩阵的大小为（ ） A.8⨯8阶矩阵 B.10⨯10阶矩阵 C.12⨯12阶矩阵 D.16⨯16阶矩阵3.坐标转换矩阵可归类为（ ）A.正交矩阵B.奇异矩阵C.正定矩阵D.对称矩阵 4.图示弹簧系统的总体刚度矩阵为（ ）A 11112322244434000000k k k k k k k k k k k k k k -⎡⎤⎢⎥-++-⎢⎥⎢⎥-+⎢⎥-+⎣⎦ B. 1111222244434000000k k k k k k k k k k k k k -⎡⎤⎢⎥-+-⎢⎥⎢⎥-+-⎢⎥-+⎣⎦C. 11112323224434340000k k k k k k k k k k k k k k k k -⎡⎤⎢⎥-++--⎢⎥⎢⎥-+-⎢⎥--+⎣⎦D. 1111223224434340000k k k k k k k k k k k k k k k -⎡⎤⎢⎥-+--⎢⎥⎢⎥-+⎢⎥--+⎣⎦5.确定已知三角形单元的局部码为1(e),2(e),3(e)，对应总码依次为3，6，4，则其单元的刚度矩阵中的元素k 24应放在总体刚度矩阵的( )。

A.1行2列B.3行12列C.6行12列D.3行6列 6.对一根只受轴向载荷的杆单元，k 12为负号的物理意义可理解为（ ） A.当节点2沿轴向产生位移时，在节点1引起的载荷与其方向相同 B.当节点2沿轴向产生位移时，在节点1引起的载荷与其方向相反 C.当节点2沿轴向产生位移时，在节点1引起的位移与其方向相同 D.当节点2沿轴向产生位移时，在节点1引起的位移与其方向相反7.平面桁架中，节点3处铅直方向位移为已知，若用置大数法引入支承条件，则应将总体刚度矩阵中的（ ）A.第3行和第3列上的所有元素换为大数AB.第6行第6列上的对角线元素乘以大数AC.第3行和第3列上的所有元素换为零D.第6行和第6列上的所有元素换为零 8.在任何一个单元内（ ）A.只有节点符合位移模式B.只有边界点符合位移模式C.只有边界点和节点符合位移模式D.单元内任意点均符合位移模式 9.平面应力问题中(Z 轴与该平面垂直)，所有非零应力分量均位于（ ） A.XY 平面内 B.XZ 平面内 C.YZ 平面内 D.XYZ 空间内 12.刚架杆单元与平面三角形单元（ ）A.单元刚度矩阵阶数不同B.局部坐标系的维数不同C.无任何不同D.节点截荷和位移分量数不同 13.图示平面结构的总体刚度矩阵［Ｋ］和竖带矩阵［K *］的元素总数分别是（ ）A.400和200B.400和160C.484和200D.484和160 14.在有限元分析中，划分单元时，在应力变化大的区域应该（ ）A.单元数量应多一些，单元尺寸小一些B.单元数量应少一些，单元尺寸大一些C.单元数量应多一些，单元尺寸大一些D.单元尺寸和数量随便确定 15.在平面应力问题中，沿板厚方向（ ）A.应变为零，但应力不为零B.应力为零，但应变不为零C.应变、应力都为零D.应变、应力都不为零16.若把平面应力问题的单元刚度矩阵改为平面应变问题的单元刚度矩阵只需将（ ） A. E 换成E/(1-μ2)，μ换成μ/(1-μ2) B. E 换成E/(1-μ2)，μ换成μ/(1-μ) C. E 换成E/(1-μ)，μ换成μ/(1-μ2) D. E 换成E/(1-μ)，μ换成μ/(1-μ) 17.图示三角形单元非节点载荷的节点等效载荷为（ ） A.F yi =-100KN F yj =-50KN F yk =0 B. F yi =-80KN F yj =-70KN F yk =0 C. F yi =-70KN F yj =-80KN F yk =0 D. F yi =-50KN F yj =-100KN F yk =018.半斜带宽矩阵r 行s 列的元素对应于竖带矩阵元素( )。

有限元法基础试题（A）一、填空题（5X2分）1.1单元刚度矩阵r = f B7 DBdQ中，矩阵fi为___________ ，矩阵£＞为__________ 。

1.2边界条件通常冇两类。

通常发生在位置完全固定不能转动的情况为_____ 边界，具体指定杏限的非零值位移的情况，如支撑的下沉，称为______ 边界。

1.3内部微元体上外力总虚功：〜pw +（、.+ 〜+ /%，）加］心办 + t + 〜什y + ~ （d\、. + ）p祷的表达式中，第一项为 __________________ 的虚功，第二项为 ___________________ 的虚功。

1.4弹簧单元的位移函数' + ;v2 = _________ 。

1.5 ~数学表込式：令＜= _______ ，d k=_____ ，k羊j，则力二、判断题（5X2分）2.1位移函数的假设合理与否将直接影响到有限元分析的计算精度、效率和可靠性。

（）2.2变形体虛功原理适川于一切结构（一维杆系、二维板、三位块体）、适用于任何力学行为的材料（线性和非线性），是变形体力学的普遍原理。

（）2.3变形体虚功原理要求力系平衡，要求虚位移协调，是在“平衡、协调”前提下功的怛等关系。

（）2.4常应变三角单元中变形矩阵是或y的阑数。

（）2.5对称单元中变形矩阵是x或;v的函数。

（）三、简答题（26分）3.1列举有限元法的优点。

（8分）3.2写岀有限单元法的分析过程。

（8分）3.3列出3种普通的旮限元单元类型。

（6分）3.4简要闸述变形体虚位移原理。

（4分）四、计算题（54分）4.1对于下图所示的弹簧组合，单元①的弹簧常数为10000N/m,单元②的弹簧常数为20000N/m，单元③的弹簧常数为10000N/m,确定各节点位移、反力以及单元②的单元力。

（10 分）4.2对于如图所示的杆组装，弹性模量E为lOGPa,杆单元长L均为2m，横截面面积A均为SXIoAn2,弹簧常数为2000kN/m，所受荷载如图。

有限元复习一、选择题（每题1分，共10分）二、判断题（每空1分，共10分）三、填空题（每空1分，共10分）三、简答题（共44分）共6题四、综述题（共26分）两题一．基本概念1. 平面应力/平面应变问题；空间问题/轴对称问题；杆梁问题；线性与非线性问题平面应力问题（1） 均匀薄板（2）载荷平行于板面且沿厚度方向均匀分布在六个应力分量中，只需要研究剩下的平行于XOY 平面的三个应力分量，即x y xy yx σσττ=、、 （000z zx xz zy yz σττττ=====，，）。

一般0z σ=，z ε并不一定等于零，但可由x σ及y σ求得，在分析问题时不必考虑。

于是只需要考虑x y xy εεγ、、三个应变分量即可。

平面应变问题（1） 纵向很长，且横截面沿纵向不变。

（2）载荷平行于横截面且沿纵向均匀分布z yz zx εγγ===只剩下三个应变分量x y xy εεγ、、。

也只需要考虑x y xy σστ、、三个应力分量即可轴对称问题物体的几何形状、约束情况及所受外力都对称于空间的某一根轴。

轴对称单元的特点（与平面三角形单元的区别）：轴对称单元为圆环体，单元与单元间为节圆相连接；节点力与节点载荷是施加于节圆上的均布力；单元边界是一回转面；应变不是常量。

在轴对称问题中，周向应变分量θε是与r 有关。

板壳问题一个方向的尺寸比另外两个方向尺寸小很多，且能承受弯矩的结构称为板壳结构，并把平分板壳结构上下表面的面称为中面。

如果中面是平面或平面组成的折平面，则称为平板；反之，中面为曲面的称为壳。

杆梁问题杆梁结构是指长度远大于其横断面尺寸的构件组成的系统。

在结构力学中常将承受轴力或扭矩的杆件称为杆，而将承受横向力和弯矩的杆件称为梁。

平面（应力应变）问题与板壳问题的区别与联系平面应力问题是指很薄的等厚度薄板，只在板边上受有平行于板面并且不沿厚度变化的面力，同时，体力也平行于板面并且不沿厚度变化。

而平面应变问题是指很长的柱形体，在柱面上受有平行于横截面并且不沿长度变化的面力，同时体力也平行于横截面并且不沿长度变化。

有限元试题及答案一、选择题1.有限元分析是一种利用计算机数值方法进行结构分析的方法，下面哪个说法是正确的？A. 有限元分析对结构的约束条件没有要求B. 有限元分析只适用于静力分析C. 有限元分析可以用来研究结构的动力响应D. 有限元分析的计算结果一定是精确的答案：C2.有限元法的基本步骤包括以下几个环节：I. 离散化II. 单元划分III. 节点连接IV. 计算材料性质V. 施加边界条件VI. 构建刚度矩阵和载荷向量VII. 求解节点位移和应力VIII. 后处理与结果分析请问选择项中正确的顺序是：A. IV – I – II – III – V – VI – VII – VIIIB. I – II – III – IV – V – VI – VII – VIIIC. II – III – V – IV – VI – I – VII – VIIID. I – III – II – IV – V – VI – VII – VIII答案：B3.在有限元分析中，单元是指将结构划分为有限个小单元来近似表示结构的方法。

下面哪个选项给出了常用的结构单元类型？A. 三角形单元，四面体单元，六面体单元B. 矩形单元，六面体单元，圆形单元C. 圆形单元，矩形单元，六面体单元D. 四面体单元，矩形单元，三角形单元答案：D二、填空题1.有限元分析中，刚度矩阵的计算需要根据单元的_________和材料的_________计算得到。

答案：几何形状，物理性质2.有限元法最常用的数学插值函数是_________函数。

答案：形函数3.在有限元分析中，自由度是指结构中的每个_________未知量。

答案：位移三、计算题1.给定如图所示的二维结构，使用有限元法进行分析。

假设结构材料为线性弹性材料，其杨氏模量为200 GPa，泊松比为0.3。

结构整体尺寸为5m x 3m，单元尺寸为1m x 1m。

分析载荷为2000 N，施加在结构的中心节点上。

《有限元法》复习题一.单选题1.平面刚架单元坐标转换矩阵的阶数为（）A．2⨯2 B．2⨯4 C．4⨯4 D．6⨯62.图示的四根杆组成的平面刚架结构，用杆单元进行有限元分析，单元和节点的划分如图示，则总体刚度矩阵的大小为（）A.8⨯8阶矩阵B.10⨯10阶矩阵C.12⨯12阶矩阵D.16⨯16阶矩阵3.坐标转换矩阵可归类为（）A.正交矩阵B.奇异矩阵C.正定矩阵D.对称矩阵4.图示弹簧系统的总体刚度矩阵为（）A111123222444340000k kk k k k kk k k kk k k-⎡⎤⎢⎥-++-⎢⎥⎢⎥-+⎢⎥-+⎣⎦B.11112222444340000k kk k k kk k k kk k k-⎡⎤⎢⎥-+-⎢⎥⎢⎥-+-⎢⎥-+⎣⎦C.111123232244343400k kk k k k k kk k k kk k k k-⎡⎤⎢⎥-++--⎢⎥⎢⎥-+-⎢⎥--+⎣⎦D.11112232244343400k kk k k k kk k k kk k k k-⎡⎤⎢⎥-+--⎢⎥⎢⎥-+⎢⎥--+⎣⎦5.确定已知三角形单元的局部码为1(e),2(e),3(e)，对应总码依次为3，6，4，则其单元的刚度矩阵中的元素k24应放在总体刚度矩阵的( )。

A.1行2列B.3行12列C.6行12列D.3行6列6.对一根只受轴向载荷的杆单元，k12为负号的物理意义可理解为（）A.当节点2沿轴向产生位移时，在节点1引起的载荷与其方向相同B.当节点2沿轴向产生位移时，在节点1引起的载荷与其方向相反C.当节点2沿轴向产生位移时，在节点1引起的位移与其方向相同D.当节点2沿轴向产生位移时，在节点1引起的位移与其方向相反7.平面桁架中，节点3处铅直方向位移为已知，若用置大数法引入支承条件，则应将总体刚度矩阵中的（）A.第3行和第3列上的所有元素换为大数AB.第6行第6列上的对角线元素乘以大数AC.第3行和第3列上的所有元素换为零D.第6行和第6列上的所有元素换为零8.在任何一个单元内（）A.只有节点符合位移模式B.只有边界点符合位移模式C.只有边界点和节点符合位移模式D.单元内任意点均符合位移模式9.平面应力问题中(Z轴与该平面垂直)，所有非零应力分量均位于（）A.XY平面内B.XZ平面内C.YZ平面内D.XYZ空间内12.刚架杆单元与平面三角形单元（）A.单元刚度矩阵阶数不同B.局部坐标系的维数不同C.无任何不同D.节点截荷和位移分量数不同13.图示平面结构的总体刚度矩阵［Ｋ］和竖带矩阵［K*］的元素总数分别是（）A.400和200B.400和160C.484和200D.484和16014.在有限元分析中，划分单元时，在应力变化大的区域应该（）A.单元数量应多一些，单元尺寸小一些B.单元数量应少一些，单元尺寸大一些C.单元数量应多一些，单元尺寸大一些D.单元尺寸和数量随便确定15.在平面应力问题中，沿板厚方向（）A.应变为零，但应力不为零B.应力为零，但应变不为零C.应变、应力都为零D.应变、应力都不为零16.若把平面应力问题的单元刚度矩阵改为平面应变问题的单元刚度矩阵只需将（）A. E换成E/(1-μ2)，μ换成μ/(1-μ2)B. E换成E/(1-μ2)，μ换成μ/(1-μ)C. E换成E/(1-μ)，μ换成μ/(1-μ2)D. E换成E/(1-μ)，μ换成μ/(1-μ)17.图示三角形单元非节点载荷的节点等效载荷为（）A.F yi=-100KN F yj=-50KN F yk=0B. F yi=-80KN F yj=-70KN F yk=0C. F yi=-70KN F yj=-80KN F yk=0D. F yi=-50KN F yj=-100KN F yk=018.半斜带宽矩阵r行s列的元素对应于竖带矩阵元素( )。

有限元试题及答案一、选择题1. 有限元法是一种数值方法，主要用于求解什么类型的数学问题？A. 线性代数方程B. 微分方程C. 积分方程D. 偏微分方程答案：D2. 在有限元分析中，以下哪项不是网格划分的基本原则？A. 网格应尽量均匀B. 网格应避免交叉C. 网格应尽量小D. 网格应适应几何形状答案：C3. 有限元方法中，单元的局部刚度矩阵可以通过以下哪种方式获得？A. 直接积分B. 矩阵乘法C. 线性插值D. 经验公式答案：A二、填空题1. 有限元方法中，______ 是指将连续的域离散化成有限数量的小单元。

答案：离散化2. 在进行有限元分析时，______ 是指在单元内部使用插值函数来近似求解场变量。

答案：近似3. 有限元法中，______ 是指在单元边界上满足的连续性条件。

答案：边界条件三、简答题1. 简述有限元法的基本步骤。

答案：有限元法的基本步骤包括：（1）定义问题域；（2）离散化问题域，生成网格；（3）为每个单元定义局部坐标系和形状函数；（4）组装全局刚度矩阵和载荷向量；（5）施加边界条件；（6）求解线性代数方程；（7）提取结果并进行后处理。

2. 描述有限元分析中的单元类型有哪些，并简述每种单元的特点。

答案：常见的单元类型包括：（1）一维单元，如杆单元和梁单元，特点是沿一个方向传递力；（2）二维单元，如三角形和四边形单元，特点是在平面内传递力；（3）三维单元，如四面体和六面体单元，特点是在空间内传递力。

每种单元都有其特定的形状函数和刚度矩阵。

四、计算题1. 给定一个简单的一维弹性杆问题，其长度为L，两端固定，中间施加集中力P。

使用有限元法求解该杆的位移和应力分布。

答案：首先，将杆离散化为一个单元。

使用一维杆单元的局部刚度矩阵和形状函数，可以推导出全局刚度矩阵。

然后，施加边界条件，即杆的两端位移为零。

最后，将集中力P转换为等效节点载荷，求解线性代数方程，得到节点位移。

应力可以通过位移和杆的截面特性计算得出。