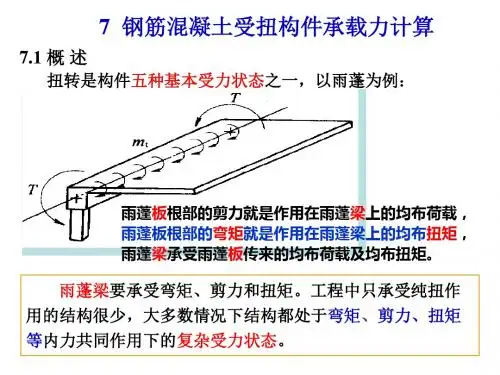
第七章 受扭构件承载力计算7.1 概述工程中的钢筋砼受扭构件有两类：● 一类是 —— 平衡扭矩：是静定结构由于荷载的直接作用所产生的扭矩，这种构件所承受的扭矩可由静力平衡条件求得，与构件的抗扭刚度无关。
如：教材图7·1a 、b 所示受檐口竖向荷载作用的挑檐梁，及受水平制动力作用的吊车梁以及平面曲梁、折线梁、螺旋楼梯等。
● 另一类是 —— 协调扭矩：是超静定结构中由于变形协调条件使截面产生的扭矩，构件所承受的扭矩与其抗扭刚度有关。
如：教材图7·2 所示现浇框架的边梁。
由于次梁在支座（边梁）处的转角产生的扭转，边梁开裂后其抗扭刚度降低，对次梁转角的约束作用减小，相应地边梁的扭矩也减小。
● 本章只讨论平衡扭转情况下的受扭构件承载力计算。
在工程结构中，直接承受扭矩、弯矩、剪力和轴向力复合作用的构件是常遇的。
但规范对弯扭、剪扭和弯剪扭构件的设计计算，是以抗弯、抗剪能力计算理论和纯扭构件的承载力计算理论为基础，采用分别计算和叠加配筋的方法进行的，故有必要先了解纯扭构件的受力性能和承载力的计算方法。
7.2 纯扭构件的受力性能7.2.1 素砼纯扭构件的受力性能素砼构件也能承受一定的扭矩。
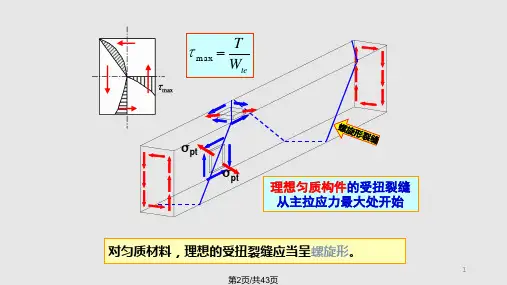
素砼构件在扭矩T 的作用下，在构件截面中产生剪应力τ及相应的主拉应力tp σ 和主压应力cp σ（教材图7·3）。
根据微元体平衡条件可知：τστσ==cp tp ,由于砼的抗拉强度远低于它的抗压程度，因此当主拉应力达到砼的抗拉强度时，即t tp f ≥=τσ时，砼就会沿垂直于主拉应力方向裂开（教材图7·3）。
所以在纯扭矩作用下的砼构件的裂缝方向总是与构件轴线成45o的角度。
并且砼开裂时的扭矩T 也就是相当于t f =τ时的扭矩，即砼纯扭构件的受扭承载力co T 。
为了求得co T ，需要建立扭矩和剪应力之间的关系，然后根据强度条件，即砼纯扭构件的破坏条件求出受扭承载力co T 。
7.2.2 素砼纯扭构件的承载力计算(一) 、弹性分析法：用弹性分析方法计算砼纯扭构件承载力时，认为砼构件为单一匀质弹性材料。
