5受扭构件承载力计算

第五章 受扭构件承载力计算一、填空题：1、钢筋混凝土弯、剪、扭构件，剪力的增加将使构件的抗扭承载力 ；扭矩的增加将使构件的抗剪承载力 。

2、由于配筋量不同，钢筋混凝土纯扭构件将发生 、 、 、 四种破坏。

3、抗扭纵筋应沿 布置，其间距 。

4、钢筋混凝土弯、剪、扭构件箍筋的最小配筋率 ，抗弯纵向钢筋的最小配筋率 ，抗扭纵向钢筋的最小配筋率 。

5、混凝土受扭构件的抗扭纵筋与箍筋的配筋强度比ς应在 范围内。

6、为了保证箍筋在整个周长上都能充分发挥抗拉作用，必须将箍筋做成 形状，且箍筋的两个端头应 。

二、判断题：1、受扭构件中抗扭钢筋有纵向钢筋和横向钢筋，它们在配筋方面可以互相弥补，即一方配置少时，可由另一方多配置一些钢筋以承担少配筋一方所承担的扭矩。

（ ）2、受扭构件设计时，为了使纵筋和箍筋都能较好地发挥作用，纵向钢筋与箍筋的配筋强度比值ς控制在7.16.0≤≤ς。

（ ）3、在混凝土纯扭构件中，混凝土的抗扭承载力和箍筋与纵筋是完全独立的变量。

（ ）4、矩形截面纯扭构件的抗扭承载力计算公式t t W f T 35.0≤+s f A A yv st cor12.1ζ只考虑混凝土和箍筋提供的抗扭承载力（ ）5、对于承受弯、剪、扭的构件，为计算方便，规范规定： t t W f T 175.0≤时，不考虑扭矩的影响，可仅按受弯构件的正截面和斜截面承载力分别进行计算。

（ ）6、对于承受弯、剪、扭的构件，为计算方便，规范规定：035.0bh f V t ≤或01875.0bh f V t +≤λ时，不考虑剪力的影响，可仅按受弯和受扭构件承载力分别进行计算。

（ ）7、弯、剪、扭构件中，按抗剪和抗扭计算分别确定所需的箍筋数量后代数相加，便得到剪扭构件的箍筋需要量。

（ ）8、对于弯、剪、扭构件，当c c tf W T bh V β25.08.00≤+加大截面尺寸或提高混凝土强度等级。

（ ） 9、对于弯、剪、扭构件，当满足t tf W T bh V 7.00≤+时，箍筋和抗扭纵筋按其最小配筋率设置。

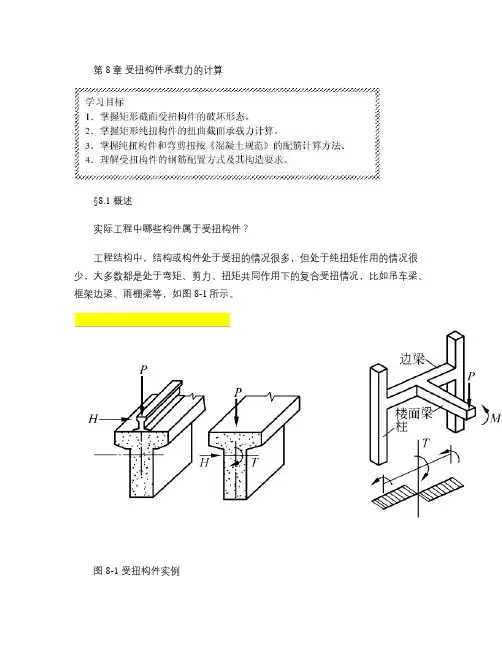
第8章受扭构件承载力的计算§8.1 概述实际工程中哪些构件属于受扭构件？工程结构中，结构或构件处于受扭的情况很多，但处于纯扭矩作用的情况很少，大多数都是处于弯矩、剪力、扭矩共同作用下的复合受扭情况，比如吊车梁、框架边梁、雨棚梁等，如图8-1所示。

图8-1 受扭构件实例受扭的两种情况：平衡扭转和协调扭转。

静定的受扭构件，由荷载产生的扭矩是由构件的静力平衡条件确定的，与受扭构件的扭转刚度无关，此时称为平衡扭转。

如图8-1（a ）所示的吊车梁，在竖向轮压和吊车横向刹车力的共同作用下，对吊车梁截面产生扭矩T 的情形即为平衡扭转问题。

对于超静定结构体系，构件上产生的扭矩除了静力平衡条件以外，还必须由相邻构件的变形协调条件才能确定，此时称为协调扭转。

如图8-1（b ）所示的框架楼面梁体系，框架的边梁和楼面梁的刚度比对边梁的扭转影响显著，当边梁刚度较大时，对楼面梁的约束就大，则楼面梁的支座弯矩就大，此支座弯矩作用在边梁上即是其承受的扭矩，该扭矩由楼面梁支承点处的转角与该处框架边梁扭转角的变形协调条件所决定，所以这种受扭情况为协调扭转。

§8.2 纯扭构件的试验研究8.2.1 破坏形态钢筋混凝土纯扭构件的最终破坏形态为：三面螺旋形受拉裂缝和一面（截面长边）的斜压破坏面，如图8-3所示。

试验研究表明，钢筋混凝土构件截面的极限扭矩比相应的素混凝土构件增大很多，但开裂扭矩增大不多。

图8-2 未开裂混凝土构件受扭图8-3 开裂混凝土构件的受力状态 8.2.2 纵筋和箍筋配置对纯扭构件破坏性态的影响受扭构件的四种破坏形态受扭构件的破坏形态与受扭纵筋和受扭箍筋配筋率的大小有关，大致可分为适筋破坏、部分超筋破坏、完全超筋破坏和少筋破坏四类。

对于正常配筋条件下的钢筋混凝土构件，在扭矩作用下，纵筋和箍筋先到达屈服强度，然后混凝土被压碎而破坏。

这种破坏与受弯构件适筋梁类似，属延性破坏。

此类受扭构件称为适筋受扭构件。

受扭构件承载力计算一、（纯扭） 某矩形截面纯扭构件，承受扭矩设计值为m KN T .18=，截面尺寸mm 500250⨯，C25混凝土，箍筋为HRB335级钢筋，纵筋为HRB400级钢筋。

混凝土净保护层厚度为c=30mm 。

环境类别为二类，试计算截面的配筋数量。

（注：2/9.11mm N f c =，2/27.1mm N f t =，2/360mm N f y =，2/300mm N f yv =）解题思路：本题属矩形截面纯扭构件的计算，先验算截面尺寸，再验算是否需要按计算配置受扭筋；若不需按计算配置抗扭钢筋，则按构造要求配筋；若需要按计算配置抗扭钢筋，可先假定ς值，然后按矩形截面钢筋混凝土纯扭构件的抗扭承载力计算公式即可求得，按步骤进行计算。

【解】2/9.11mm N f c =，2/27.1mm N f t =，2/360mm N f y =，2/300mm N f yv =，混凝土保护层为mm 301、验算截面尺寸是否满足要求362210021.13)2505003(6250)3(6mm b h b W t ⨯=-⨯⨯=-= 975.29.110.125.025.0728.110021.138.010188.066=⨯⨯==⨯⨯⨯=c c t f W T β 故截面尺寸满足要求2、验算是否按计算配置抗扭钢筋m KN T m KNN W f t t .18.58.1110021.1327.17.07.06==⨯⨯⨯=故需按计算配置受扭钢筋3、抗扭箍筋的计算mm b cor 190230250=⨯-=，mm h cor 440230500=⨯-=（1）假定1.1=ζ（2）由t t W f T 35.0≤+s f A A yv st cor 12.1ζ得387.04401903001.12.110021.1327.135.010182.135.0661=⨯⨯⨯⨯⨯⨯-⨯=-=cor yv t t st A f W f T s A ς（3）箍筋直径及间距的确定选用8Φ箍筋（213.50mm A sv =），双肢箍，2=n则mm A s st 130387.03.50387.01=== 取mm s 120=<mm s 200max = （满足构造要求）即所配箍筋为120@8Φ（4）验算抗扭箍的配筋率%12.030027.128.028.0%34.01202503.5022min ,1===≥=⨯⨯==yv t sv st sv f f bs A ρρ 满足要求4、抗扭纵筋的计算（1）按cor st yv stl y st yv corstly A f s A f s A f A f μμζ11/==得 214841203.503604401903001.1mm s A f u f A st y cor yv stl =⋅⨯⨯⨯=⋅=ς （2）验算抗扭纵筋配筋率%30.036027.185.085.0%387.0500250484min ,=⨯==≥=⨯==y t tl stl tl f f bh A ρρ 满足要求（3）选筋：选用（2678mm A s =）弯、剪、扭构件计算三、 某雨篷梁，承受弯矩、剪力、扭矩设计值为m KN M .25=， KN V 40=，m KN T .6=，截面尺寸mm 240240⨯，C25混凝土，箍筋为HRB335级钢筋，纵筋为HRB400级钢筋。

桥梁受扭构件破坏特征及承载力计算桥梁是连接两个地理位置的重要交通设施，它承载着车辆和行人的重量。

桥梁的承载力是指其能够支撑的最大荷载，而桥梁受扭构件是桥梁中的重要组成部分。

本文将介绍桥梁受扭构件的破坏特征和承载力计算方法。

一、桥梁受扭构件的破坏特征1.剪切破坏：扭转会产生剪应力，当剪应力大于材料的抗剪强度时，受扭构件会发生剪切破坏。

2.扭转破坏：在受扭构件上，扭转力作用会使其发生相对旋转，当达到一定角度时，受扭构件会失去承载能力，发生扭转破坏。

3.弯曲破坏：受扭构件在受到扭矩力矩作用时，由于材料的抗弯刚度有限，会发生弯曲破坏。

4.龙骨翻转：龙骨是支撑桥面板的主要构件，受到扭矩作用时，龙骨可能会翻转，导致桥面板的破坏。

1.线性弹性理论法：在这种计算方法中，假设受扭构件材料的应力-应变关系服从线性弹性的规律，利用弹性力学理论进行力学计算，得到受扭构件的最大承载力。

2.极限强度理论法：这种计算方法基于构件材料的极限强度，假设受扭构件在超过一定弯曲角度后失去承载能力，利用建筑结构力学知识和试验数据，根据构件的几何形状、材料性能和边界条件等因素，确定承载力。

无论采用何种计算方法，桥梁受扭构件的承载力计算都需要考虑以下因素：1.受扭构件的几何形状和材料性能。

2.受扭构件所受的荷载类型和大小。

3.受扭构件所处的边界条件和约束。

4.受扭构件的安全系数。

通过对以上因素的综合考虑和计算，可以得到桥梁受扭构件的承载力。

在实际设计和施工中，为了保证桥梁的安全性和稳定性，通常会采用一定的安全系数，并结合实际情况进行合理的调整。

总之，桥梁受扭构件的破坏特征和承载力计算是保证桥梁安全可靠运行的重要内容。

通过合理的设计和计算，可以确保桥梁受扭构件具备足够的承载能力，满足实际的使用需求。

钢筋混凝土受扭构件承载力设计计算摘要：结合桥梁设计工作实践经验论述了受扭构件承载力的计算方法和计算公式，结合具体实例，提出了钢筋混凝土受扭构件设计及承载力的计算方法及适用范围，以供设计者参考借鉴。

关键词：桥梁工程桥梁构件混凝土受扭构件承载力设计内力计算桥梁工程中扭转构件其受力的基本形式之一，钢筋混凝土结构中常见的构件形式，例如现浇框架边梁或折梁等结构构件都是受扭构件。

受扭构件根据截面上存在的内力情况可分为纯扭、剪扭、弯扭、弯剪扭等多种受力情况。

在实际工程中，纯扭、剪扭、弯扭的受力情况较少，弯剪扭的受力情况则较普遍。

因此，在桥梁结构设计工作中构件的内力计算至关重要。

1 钢筋混凝土矩形截面纯扭构件的设计与计算（1）开裂扭矩的计算：纯扭构件的扭曲截面承载力计算中，首先需要计算构件的开裂扭矩。

如果扭矩大于构件的开裂扭矩，则还要按计算配置受扭纵筋和箍筋，以满足构件的承载力要求。

否则，应按构造要求配置受扭钢筋。

在《公路钢筋混凝土及应力混凝土桥涵设计规范》(JTG D62-2004)中规定，钢筋混凝土矩形截面纯扭构件的开裂扭矩可用公式计算：2 钢筋混凝土弯、剪、扭构件的配筋设计与计算在《公路钢筋混凝土及应力混凝土桥涵设计规范》(JTG D62-2004)中规定，弯、剪、扭构件的配筋计算，也采取叠加计算的截面设计简化方法。

（1）受剪扭的构件承载力计算：现行设计规范中规定，钢筋混凝土剪扭构件的承载能力，一般按受扭和受剪构件分别计算承载能力，然后再它们叠加起来。

但是，剪、扭共同作用的构件，剪力和扭矩对混凝土和箍筋的承载能力均有一定影响。

如果采取简单地叠加，对箍筋和混凝土尤其是混凝土是偏于不安全的。

构件在剪扭的共同作用下，其截面的某一受压区内承受剪切和扭转应力的双重作用，这不仅会降低构件内混凝土的抗剪和抗扭能力，而且分别小于单独受剪和受扭时相应的承载能力。

由于受扭钢筋混凝土构件的受力情况比较复杂，所以对箍筋所承担的承载能力采取简单叠加，混凝土的抗扭和抗剪承载能力考虑其相互影响，在混凝土的抗扭承载能力计算式中，应引入剪扭构件混凝土承载能力的降低系数。

钢筋混凝土受扭构件承载力计算1．钢筋混凝土构件受扭状态可以分为哪两大类？何谓平衡扭转和协调扭转？答：钢筋混凝土构件受扭状态可以分为两大类，平衡扭转和协调扭转。

平衡扭转是指其扭矩依据构件扭矩平衡关系，由荷载直接确定且与构件的扭转刚度无关的受扭状态；例如支承悬臂板的梁及吊车梁等承受的扭矩既为平衡扭转。

对于平衡扭转，构件必须具有足够的受扭承载力，否则将因不能与作用扭矩平衡而引起破坏。

协调扭转是指作用在构件上的扭矩由平衡关系与变形协调条件共同确定的受扭状态；例如框架中的边梁，受到次梁负弯矩的作用，在边梁上引起的扭转。

对于协调扭矩，在受力过程中，因为混凝土和钢筋的非线性性能，尤其是混凝土的开裂和钢筋的屈服，会引起内力重分布。

2．钢筋混凝土构件在纯扭作用下的破坏状态随配筋状况的不同大致可分为哪四种类型？各有何破坏特点？答：钢筋混凝土构件在纯扭作用下的破坏状态随配筋状况的不同大致可分为适筋破坏、部分超筋破坏、超筋破坏、少筋破坏四种类型。

它们的何破坏特点如下：（1）适筋破坏正常配筋条件下的钢筋混凝土构件，在外扭矩的作用下，纵筋和箍筋首先达到屈服强度，然后混凝土压碎而破坏。

这种破坏与受弯构件的适筋梁类似，属延性破坏，此类受扭构件称为适筋构件；（2）部分超筋破坏当纵筋和箍筋配筋比率相差较大，破坏时仅配筋率较小的纵筋或箍筋达到屈服强度，而另一种钢筋不屈服，此类构件破坏时，亦具有一定的延性，但比适筋构件的延性小，此类构件称为部分超配筋构件；这类构件应在设计中予以避免。

（3）超筋破坏当纵筋和箍筋配筋率都过高，会发生纵筋和箍筋都没有达到屈服强度，而混凝土先行压坏的现象，这种现象类似于受弯构件的超筋脆性破坏，这种受扭构件称为超配筋构件；这类构件应在设计中予以避免。

（4）少筋破坏当纵筋和箍筋配置均过少，一旦裂缝出现，构件会立即发生破坏，此时纵筋和箍筋应力不仅能达到屈服强度而且可能进入强化阶段，配筋只能稍稍延缓构件的破坏，其破坏性质与素混凝土矩形截面构件相似，破坏过程急速而突然，破坏扭矩基本上等于开裂扭矩。