点与圆的位置关系 课件

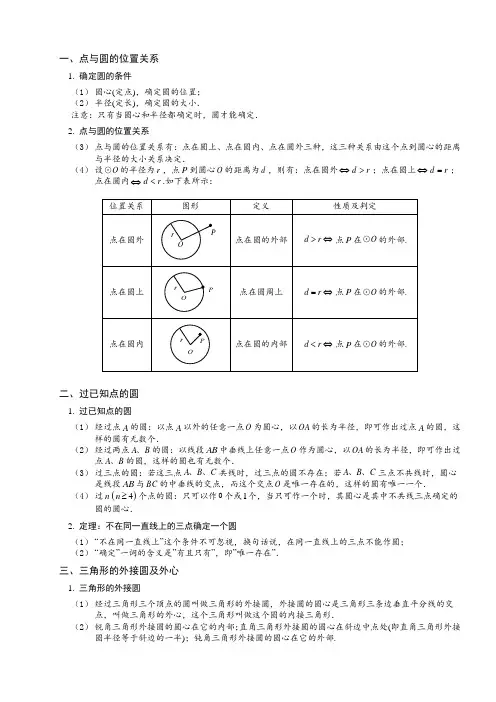
一、点与圆的位置关系1.确定圆的条件（1）圆心(定点)，确定圆的位置；（2）半径(定长)，确定圆的大小．注意：只有当圆心和半径都确定时，圆才能确定．2.点与圆的位置关系（3）点与圆的位置关系有：点在圆上、点在圆内、点在圆外三种，这三种关系由这个点到圆心的距离与半径的大小关系决定．（4）设O=；⊙的半径为r，点P到圆心O的距离为d，则有：点在圆外⇔d r>；点在圆上⇔d r 点在圆内⇔d r<.如下表所示：二、过已知点的圆1.过已知点的圆（1）经过点A的圆：以点A以外的任意一点O为圆心，以OA的长为半径，即可作出过点A的圆，这样的圆有无数个．（2）经过两点A B、的圆：以线段AB中垂线上任意一点O作为圆心，以OA的长为半径，即可作出过点A B、的圆，这样的圆也有无数个．（3）过三点的圆：若这三点A B C、、三点不共线时，圆心、、共线时，过三点的圆不存在；若A B C是线段AB与BC的中垂线的交点，而这个交点O是唯一存在的，这样的圆有唯一一个．（4）过n()4n≥个点的圆：只可以作0个或1个，当只可作一个时，其圆心是其中不共线三点确定的圆的圆心．2.定理：不在同一直线上的三点确定一个圆（1）“不在同一直线上”这个条件不可忽视，换句话说，在同一直线上的三点不能作圆；（2）“确定”一词的含义是”有且只有”，即”唯一存在”．三、三角形的外接圆及外心1.三角形的外接圆（1）经过三角形三个顶点的圆叫做三角形的外接圆，外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心，这个三角形叫做这个圆的内接三角形．（2）锐角三角形外接圆的圆心在它的内部；直角三角形外接圆的圆心在斜边中点处(即直角三角形外接圆半径等于斜边的一半)；钝角三角形外接圆的圆心在它的外部.2. 三角形外心的性质（1） 三角形的外心是指外接圆的圆心，它是三角形三边垂直平分线的交点，它到三角形各顶点的距离相等； （2） 三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合.一、点与圆的位置关系【例1】 已知圆内一点到圆周上的点的最大距离是7，最小距离是5，则该圆的半径是( )A ．2B ．6C ．12D ．7【巩固】1、一个已知点到圆周上的点的最大距离为5cm ，最小距离为1cm ，则此圆的半径为______．2、若⊙O 所在平面内一点P 到⊙O 上的点的最大距离为a ，最小距离为b （a>b ），则此圆的半径为（ ）DA ．2b a + B ．2ba - C ．22ba b a -+或 D ．b a b a -+或3、定义：定点A 与O ⊙上的任意一点之间的距离的最小值称为点A 与O ⊙之间的距离．现有一矩形ABCD如图，14cm 12cm AB BC ==，，K ⊙与矩形的边AB BC CD 、、分别相切于点E F G 、、，则点A 与K ⊙的距离为______________．【例2】 已知ABC ∆中，90C ∠=︒，2AC =，3BC =，AB 的中点为M ，⑴以C 为圆心，2为半径作C ⊙，则点A ，B ，M 与C ⊙的位置关系如何？ ⑵若以C 为圆心作C ⊙，使A ，B ，M 三点至少有一点在C ⊙内，且至少有一点在C ⊙外，求C⊙半径r 的取值范围．M CBA【巩固】1、Rt ABC ∆的两条直角边3BC =，4AC =，斜边AB 上的高为CD ，若以C 为圆心，分别以12r =，2 2.4r =，33r =为半径作圆，试判断D 点与这三个圆的位置关系.DCBA2、在ABC ∆中，90C ∠=︒，4AC =，5AB =，以点C 为圆心，以r 为半径作圆，请回答下列问题，并说明理由.⑴当r 取何值时，点A 在C ⊙上，且点B 在C ⊙内部？⑵当r 在什么范围内取值时，点A 在C ⊙外部，且点B 在C ⊙的内部？ ⑶是否存在这样的实数r ，使得点B 在C ⊙上，且点A 在C ⊙内部？CBA二、过三点的圆【例3】 如图，四边形ABCD 中，AB AC AD ==，若7613CAD BDC ∠=︒∠=︒，，则CBD ∠=_________，BAC ∠=__________．DCBA【例4】 如图，在平面直角坐标系中，O '与两坐标轴分别交于A B C D ，，，四点，已知：()60A ，，()03B -，，()20C -，，则点D 的坐标是（ ） A ．()02，B ．()03，C ．()04，D ．()05，三、三角形的外接圆及外心【例5】 如图，ABC ∆内接于O ⊙，120BAC ∠=︒，AB AC =，BD 为O ⊙的直径，6AD =，则BC =.【巩固】等边三角形的外接圆的半径等于边长的（ ）倍．ABCD ．12【例6】 设Rt ABC ∆的两条直角边长分别为3，4，则此直角三角形的内切圆半径为 ，外接圆半径为 ．【巩固】1、如图，直角坐标系中一条圆弧经过网格点A B C ，，，其中B 点的坐标为()44，，则该圆弧所在圆的圆心的坐标为 ．2、ABC ∆中，10AB AC ==，12BC =，求其外接圆的半径．【例7】 在等腰ABC ∆中，AB BC =，BH 是高，点M 是边AB 的中点，而经过点B ，M 于C 的圆同BH的交点是K ，求证32BK R =，其中R 是ABC ∆的外接圆半径．【巩固】1、已知∆ABC 中，=AB AC ，D 是∆ABC 外接圆劣弧AC 上的点(不与点A C ，重合)，延长BD 至E ．⑴求证：AD的延长线平分∠CDE；⑵若30∠=︒BAC，∆ABC中BC边上的高为2∆ABC外接圆的面积．AB CD E2、已知如图，ACD∆的外角平分线CB交其外接圆于B，连接BA、BD，求证：BA BD=．N一、直线与圆的位置关系设O⊙的半径为r，圆心O到直线l的距离为d，则直线和圆的位置关系如下表：切线的性质定理：圆的切线垂直于过切点的半径．推论1：经过圆心且垂直于切线的直线必经过切点．推论2：经过切点且垂直于切线的直线必经过圆心．注意：这个定理共有三个条件，即一条直线满足：①垂直于切线②过切点③过圆心①过圆心，过切点⇒垂直于切线．AB过圆心，AB过切点M，则AB l⊥．②过圆心，垂直于切线⇒过切点．AB过圆心，AB l⊥，则AB过切点M．③过切点，垂直于切线⇒过圆心．AB l⊥，AB过切点M，则AB过圆心．l3.切线的判定（1）定义法：和圆只有一个公共点的直线是圆的切线；（2）距离法：和圆心距离等于半径的直线是圆的切线；（3）定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．注意：定理的题设是①“经过半径外端”，②“垂直于半径”，两个条件缺一不可；定理的结论是“直线是圆的切线”．因此，证明一条直线是圆的切线有两个思路：①连接半径，证直线与此半径垂直；②作垂直，证垂直在圆上．l4.切线长和切线长定理（1）切线长：在经过圆外一点的圆的切线上，这点和切点之间的线段的长，叫做这点到圆的切线长．（2）切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．三、三角形的内切圆1.三角形的内切圆：和三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．2. 多边形的内切圆：和多边形的各边都相切的圆叫做多边形的内切圆，这个多边形叫做圆的外切多边形．3. 直角三角形内切圆的半径与三边的关系cb acbaO F ED CACBAC B A设a 、b 、c 分别为ABC △中A ∠、B ∠、C ∠的对边，面积为S ，则内切圆半径为sr p=，其中()12p a b c =++．若90C ∠=︒，则()12r a b c =+-． 一、直线与圆位置关系的确定【例1】 如图，已知⊙O 是以数轴的原点O 为圆心，半径为1的圆，45AOB ∠=︒，点P 在数轴上运动，若过点P 且与OA 平行的直线与⊙O 有公共点，设OP x =，则x 的取值范围是A ．0≤x B．≤x C ．－1≤x ≤1D ．x【例2】 Rt ABC ∆中，90C ∠=︒，3cm AC =，4cm BC =，给出下列三个结论： ①以点C 为圆心，3 cm长为半径的圆与AB 相离；②以点C 为圆心，4cm 长为半径的圆与AB 相切；③以点C 为圆心，5cm 长为半径的圆与AB 相交．上述结论中正确的个数是（ ） A ．0个 B ．l 个 C ．2个 D ．3个【巩固】在Rt ABC ∆中，90C ∠=︒，12cm AC =，16cm BC =，以点C 为圆心，r 为半径的圆和AB 有怎样的位置关系？为什么？⑴ 9cm r =；⑵10cm r =；⑶9.6cm r =．DCBA【例3】 如下左图，在直角梯形ABCD 中，AD BC ∥，90C =︒∠，且AB AD BC >+，AB 是O 的直径，则直线CD 与O 的位置关系为( ) A ．相离 B ．相切 C ．相交 D ．无法确定【巩固】如图，BC是半圆O的直径，点D是半圆上的一点，过点D作O的切线AD，BA DA⊥，10BC=，4AD=，那么直线CE与以点O为圆心，52为半径的圆的位置关系是．二、切线的性质及判定【例4】已知：O为BAC∠平分线上一点，OD AB⊥于D，以O为圆心．以OD为半径作圆O．求证：O⊙与AC相切．【巩固】如图，ABC∆为等腰三角形，AB AC=，O是底边BC的中点，O⊙与腰AB相切于点D，求证AC 与O⊙相切．【例5】已知：如图，ABC∆内接于O，AD是过A的一条射线，且B CAD∠=∠．求证：AD是O的切线．【巩固】已知：如图，AB是O⊙的直径，C为O⊙上一点，MN过C点，AD MN⊥于D，AC平分DAB∠．求证：MN为O⊙的切线．【例6】如图，已知OA是O⊙的半径，B是OA中点，BC OA⊥，P是OA延长线上一点，且PA AC=．求证：PC是O⊙的切线．【巩固】如图，AB是O⊙的直径，C点在圆上，CD AB⊥于D．P在BA延长线上，且PCA ACD∠=∠．求证：PC是O⊙的切线．BP【例7】如图，O⊙是Rt ABC∆的外接圆，90ABC∠=︒，点P是圆外一点，PA切O⊙于点A，且PA PB=．（1）求证：PB是O⊙的切线．（2）已知1PA BC=，求O⊙的半径．【巩固】1、如图，AB 为O ⊙的直径，D 是BC 的中点，DE AC ⊥交AC 的延长线于E ，O ⊙的切线BF 交AD 的延长线于点F ．求证：DE 是O ⊙的切线；FAB2、如图，已知O 是正方形ABCD 对角线上一点，以O 为圆心、OA 长为半径的O ⊙与BC 相切于M ，与AB 、AD 分别相交于E 、F ．（1）求证：CD 与O ⊙相切．（2）若正方形ABCD 的边长为1，求O ⊙的半径．【例8】 如图，AB BC =，以AB 为直径的O ⊙交AC 于点D ，过D 作DE BC ⊥，垂足为E ．（1）求证：DE 是O ⊙的切线；（2）作DG AB ⊥交O ⊙于G ，垂足为F ，若308A AB ∠=︒=，，求弦DG 的长．【巩固】如图，AC 为O ⊙的直径，B 是O ⊙外一点，AB 交O ⊙于E 点，过E 点作O ⊙的切线，交BC 于D 点，DE DC =，作EF AC ⊥于F 点，交AD 于M 点．求证：BC 是O ⊙的切线；D CB A【例9】 如图，AB 是O 的直径，30BAC ∠=︒，M 是OA 上一点，过M 作AB 的垂线交AC 于点N ，交BC 的延长线于点E ，直线CF 交EN 于点F ，且ECF E ∠=∠． （1）证明CF 是O 的切线；（2）设O 的半径为1，且AC CE =，求MO 的长．A1. 已知60ABC ∠=︒，点O 在ABC ∠的平分线上，5cm OB =，以O 为圆心3cm 为半径作圆，则O 与BC 的位置关系是________．2.如图，半径为3cm 的O ⊙切直线AC 于B ，3cm AB BC =，，则AOC ∠的度数是 ．3.如图所示在Rt ABC ∆中，90B ∠=︒，A ∠的平分线交BC 于D ，E 为AB 上一点，DE DC =，以D 为圆心，以DB 的长为半径画圆．求证：（1）AC 是D ⊙的切线；（2）AB EB AC +=．E B4.如图，四边形ABCD 内接于O ，BD 是O 的直径，AE CD ⊥，垂足为E ，DA 平分BDE ∠．（1）求证：AE 是O 的切线；（2）若301cm DBC DE ∠==，，求BD 的长．5.如图，在以O 为圆心的两个同心圆中，AB 经过圆心O ，且与小圆相交于点A 、与大圆相交于点B ．小圆的切线AC 与大圆相交于点D ，且CO 平分ACB ∠． ⑴ 试判断BC 所在直线与小圆的位置关系，并说明理由； ⑵ 试判断线段AC AD BC 、、之间的数量关系，并说明理由；⑶ 若8cm 10cm AB BC ==，，求大圆与小圆围成的圆环的面积．。