投影与三视图
- 格式:doc
- 大小:66.18 KB
- 文档页数:5



投影与视图;一.投影:1.光源点光源:像手电筒、路灯、台灯都可以看成一个点光源。
平行光源:太阳光可以看成是一个平行光源2.概念定义:一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影,照射光线叫做投影线,投影所在的平面叫做投影面。
(1)平行投影:由平行光线(太阳的光线是平行光线)形成的投影。
(2)中心投影:由同一点(点光源发出的光线)形成的投影。
(3)两者区别与联系:区别光线物体与投影面平行联系时的投影平行投影平行的投射线全等都是物体在光线的照射下,在某中心投影从一点出发的投射线放大(位似变换)个平面内形成的影子。
(即都是投影)3.投影知识点:测量同一时刻物体的高度和影长时:①若两物体的高度之比等于影长之比时,则这两个物体的影子是平行投影。
②若两物体的高度之比不等于影长之比时,则这两个物体的影子是中心投影4.投影的性质:①将两个等高物体垂直于与地面放置时,离点光源较近的物体的影子较短,反之则越长。
②将两个等高物体平行于与地面放置时,离点光源较近的物体的影子较长,反之则越短。
5.易错题整理:1)直线的平行投影一定是直线(×)原因:2)矩形的投影一定是矩形(×)原因:3)一个圆在平面上的投影一定是圆。
(×)原因:二.视图:1.概念:用正投影的方法绘制的物体在投影面上的图形,称为物体的视图。
2.分类:视图有:主视图、左视图、俯视图3.正方体的主要视图及展开:正方体的展开图有11种:1)1-4-1型:6种 2)2-3-1型:3种3)2-2-2型:1种 4) 3-3 型:1种4.看视图确定物体有多少正方体组成:在俯视图中画圈标注法,取较小数值的和。


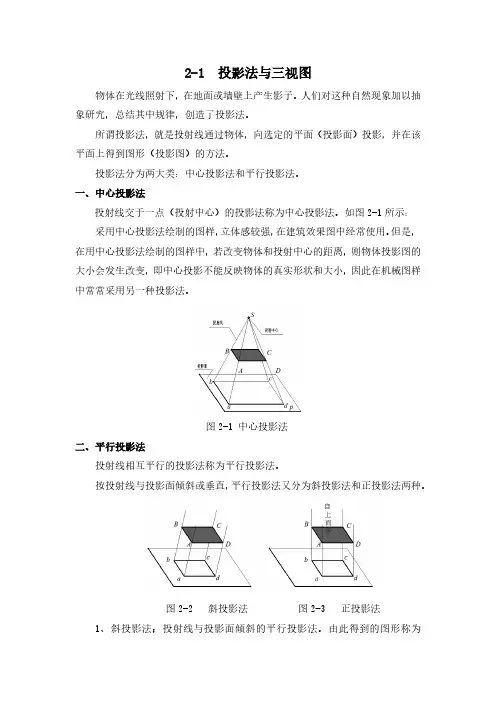
2-1 投影法与三视图物体在光线照射下,在地面或墙壁上产生影子。
人们对这种自然现象加以抽象研究,总结其中规律,创造了投影法。
所谓投影法,就是投射线通过物体,向选定的平面(投影面)投影,并在该平面上得到图形(投影图)的方法。
投影法分为两大类:中心投影法和平行投影法。
一、中心投影法投射线交于一点(投射中心)的投影法称为中心投影法。
如图2-1所示:采用中心投影法绘制的图样,立体感较强,在建筑效果图中经常使用。
但是,在用中心投影法绘制的图样中,若改变物体和投射中心的距离,则物体投影图的大小会发生改变,即中心投影不能反映物体的真实形状和大小,因此在机械图样中常常采用另一种投影法。
图2-1 中心投影法二、平行投影法投射线相互平行的投影法称为平行投影法。
按投射线与投影面倾斜或垂直,平行投影法又分为斜投影法和正投影法两种。
图2-2 斜投影法图2-3 正投影法1、斜投影法:投射线与投影面倾斜的平行投影法。
由此得到的图形称为斜投影图(简称斜投影)。
如图2-2所示。
2、正投影法:投射线与投影面垂直的平行投影法。
由此得到的图形称为正投影图(简称正投影)。
如图2-3所示。
正投影图度量性好,作图简单,机械图样常常采用正投影法绘制。
三、正投影的基本特性(单投影面)1、真实性:当物体上的平面(或直线)与投影面平行时,其投影反映实形(或实长)。
如图2-4(a)。
2、积聚性:当物体上的平面(或直线)与投影面垂直时,其投影积聚成直线(或点)。
如图2-4(b)。
3、类似性(亦称收缩性):当物体上的平面(或直线)与投影面倾斜时,其投影收缩成原来形状的类似形。
如图2-4(c)。
图2-4 正投影的特性四、三视图的形成及投影规律1、三投影面体系一般情况下,物体的一个投影图(二维)不能准确地反映物体(三维)的完整形状,如图2-5所示。
要想准确表达物体的结构形状,就必须增加投影图。
工程上常采用在三投影面体系中得到的三面投影图来表达物体的形状,如图2-6所示。
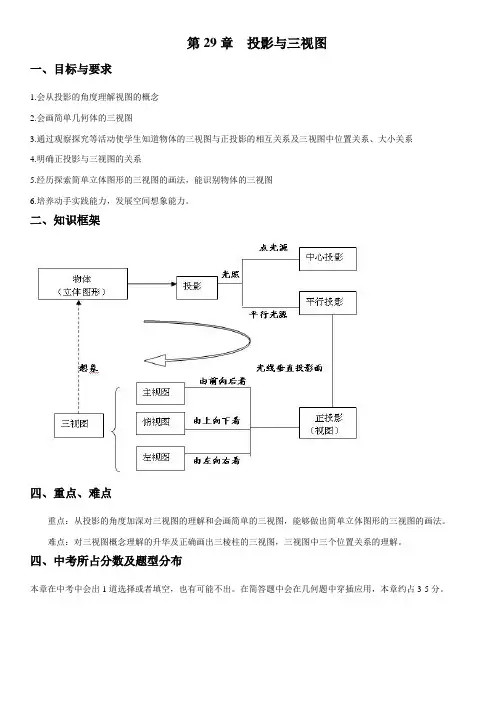
第29章投影与三视图一、目标与要求1.会从投影的角度理解视图的概念2.会画简单几何体的三视图3.通过观察探究等活动使学生知道物体的三视图与正投影的相互关系及三视图中位置关系、大小关系4.明确正投影与三视图的关系5.经历探索简单立体图形的三视图的画法,能识别物体的三视图6.培养动手实践能力,发展空间想象能力。
二、知识框架四、重点、难点重点:从投影的角度加深对三视图的理解和会画简单的三视图,能够做出简单立体图形的三视图的画法。
难点:对三视图概念理解的升华及正确画出三棱柱的三视图,三视图中三个位置关系的理解。
四、中考所占分数及题型分布本章在中考中会出1道选择或者填空,也有可能不出。
在简答题中会在几何题中穿插应用,本章约占3-5分。
第29章 投影与三视图29.1 投影1.投影:用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影,照射光线叫做投影线,投影所在的平面叫做投影面。
2.平行投影:有时光线是一组互相平行的射线,例如太阳光或探照灯光的一束光中的光线。
由平行光线形成的投影是平行投影.3.中心投影:由同一点(点光源发出的光线)形成的投影叫做中心投影。
4.正投影:投影线垂直于投影面产生的投影叫做正投影。
例.把一根直的细铁丝(记为线段AB)放在三个不同位置:(1)铁丝平行于投影面;(2)铁丝倾斜于投影面;(3)铁丝垂直于投影面(铁丝不一定要与投影面有公共点).三种情形下铁丝的正投影各是什么形状?通过观察、测量可知:(1)当线段AB 平行于投影面P 时,它的正投影是线段11A B ,线段与它的投影的大小关系为11AB A B =;(2)当线段AB 倾斜于投影面P 时,它的正投影是线段22A B ,线段与它的投影的大小关系为22AB A B =;(3)当线段AB 垂直于投影面P 时,它的正投影是一个点3A .例.把一正方形硬纸板P (记正方形ABCD )放在三个不同位置:(1)纸板平行于投影面;(2)纸板倾斜于投影面;(3)纸板垂直于投影面。



三维目标
1.掌握平行投影和中心投影,了解空间图形的不同表示形式和相互转化,发展学生的空间想象能力,培养学生转化与化归的数学思想方法.
2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,并能识别上述三视图表示的立体模型,会用材料(如纸板)制作模型,提高学生识图和画图的能力,培养其探究精神和意识.
1知识与技能:了解中心投影与平行投影;能画出简单几何体的三视图;能识别三视图所表示的空间几何体。
2过程与方法:通过学生自己的亲身实践,动手作图来完成“观察、思考”栏目中提出的问题。
3情感态度与价值观:培养学生空间想象能力和动手实践能力,激发学习兴趣。
二、教学重点:画出简单组合体的三视图
三、教学难点:识别三视图所表示的空间几何体
重点难点
教学重点:画出简单组合体的三视图,给出三视图和直观图,还原或想象出原实际图的结构特征.
教学难点:识别三视图所表示的几何体.
一、创设情景,揭开课题
“横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中”。
这是北宋诗人苏轼的一首诗,同学们,苏轼是怎样观察庐山的呢?对,横看,侧看,近看,远看,身处山中看。
这说明从不同的角度看同一物体视觉的效果可能不同,要比较真实地反映出物体的结构特征,我们可从多角度观看物体。
在上一
节我们认识了空间几何体的结构特征,如何将这些空间几何体画在纸上,并体现立体感呢?这堂课我们主要学习中心投影与平行投影及空间几何体的三视图。
(点出课题:投影和三视图).
二、新知识探究
1. 中心投影与平行投影:
我们知道,物体在灯光或日光的照射下,就会在地面或墙壁上产生影子,这是一种自然现象。
投影就是由这类自然现象抽象出来的。
所谓投影,是一个不透明物体在光的照射下,在物体后面的屏幕上留下这个物体的影子,这种现象叫做投影.其中的光线叫做投影线,留下物体影子的屏幕叫做投影面.生活中有许多利用投影的例子,如手影表演,皮影戏等。
不同的光源发出的光线是有差异的,其中灯泡发出的光线与太阳发出的光线有什么不同?我们把光由一点向外散射形成的投影叫做中心投影,把在一束平行光线照射下形成的投影叫做平行投影,在平行投影中,投影线正对着投影面时叫做正投影,投影方向与投影面倾斜的投影叫做斜投影。
那么用灯泡照射物体和太阳照射物体形成的投影分别是哪种投影?
中心投影的特点:中心投影的投影大小与物体和投影面之间的距离有关。
平行投影的特点:与投影面平行的平面图形留下的影子, 与物体的形状大小完全相同,与物体和投影面之间的距离无关。
把一个空间几何体投影到一个平面上,可以获得一个平面图形. 但只有一个
平面图形难以把握几何体的全貌,因此我们需要从多个角度进行投影,这样就能较好地把握几何体的形状和大小,通常选择三种正投影,即正面、侧面和上面。
2.三视图:
光线从几何体的前面向后面正投影,得到投影图,这种投影图叫做几何体的正视图(也叫主视图);光线从几何体的上面向下面正投影,得到投影图,这种投影图叫做几何体的俯视图;光线从几何体的左面向右面正投影,得到投影图,这种投影图叫做几何体的侧视图(也叫左视图);几何体的正视图、侧视图和俯视图统称为几何体的三视图。
如图,设长方体的长、宽、高分别为a 、b 、c ,那么其三视图分别是什么?
三视图的位置关系:一般地,侧视图在正视图的右边;俯视图在正视图的下边.. 观察长方体的三视图,你能得出同一个几何体的正视图、侧视图和俯视图在形状、大小方面的关系吗?
投影规律:(1)正视图反映了物体的高度和长度;
俯视图反映了物体的长度和宽度;
侧视图反映了物体的高度和宽度.
(2)一个几何体的正视图和侧视图高度一样,正视图和俯视图长度一样,侧视图和俯视图宽度一样,即正、俯视图——长对正;主、侧视图——高平齐;俯、侧视图——宽相等. 正视图 侧视图 俯视图
等
三、巩固新知
例1 说说圆柱、圆锥、圆台、球的三视图分别是什么?
例2 请同学们画下面这两个圆台的三视图,如果你认为这两个圆台的三视图一样,画一个就可以;如果你认为不一样,请分别画出来。
探究:在以上画三视图的过程中应该注意什么?
注意:
(1)长对正,高平齐,宽相等。
(2)画几何体的三视图时, 能看见的轮廓和棱用实线表示, 不能看见的轮廓和棱用虚线表示。
(3)三视图的位置关系:侧视图在正视图的右边;俯视图在正视图的下边。
例 3图(1)、(2)分别是两个几何体的三视图,你能说出它们对应的几何体的名称吗?
使学生掌握由视体到立体图型的方法,培养空间想象能力。
探究:实践动手作图:
讲台上放球、长方体实物,教师引导学生用类比方法画出简单组合体的三视图
(1)画出球放在长方体上的三视图
正视图 侧视图
俯视图 (2) 正视图 侧视图 俯视图 (1)
(2)画出矿泉水瓶(实物放在桌面上)的三视图
学生画完后,可把自己的作品展示并与同学交流,总结自己的作图心得。
四课堂小结
本节课学习了:
1.中心投影和平行投影.
2.简单几何体和组合体的三视图的画法及其投影规律.
3.由三视图判断原几何体的结构特征.
4.空间想象能力,逆向思维能力
重点讲解由三视图判断几何体的结构特征,
感谢您的阅读,祝您生活愉快。