10-回路电流法—课件文档

-US1 + IL1R1 + (IL1 - IL2) R2 =0
(IL2-IL1) R2 +IL2R3+ US3 =0
例1 列写回路电流方程
I1
a I3
解I：-US1 + IL1R1 + (IL1 - IL2) R2 =0 (IL2-IL1) R2 +IL2R3+ US3 =0
R1 +
il1 R2
I2 il2
uS1
–
R3 将解I的结果，以回路电路为未知量整理得 +
–uS3 (R1 R2 )I L1 R2 I L2 U S1
b 选取回路如图所示
(R3 R2 )I L2 R2I L1 U S3
解II：
总结以上结果的规律，记住自阻、互阻的概念，背过公式，直接列 出以上方程，便是解法II：
二、 网孔电流法：（仅适用于平面电路）
对平面电路，若以网孔为独立回路，此时回路电流也
称为网孔电流，对应的分析方法称为网孔电流法。 若以自然网孔为回路，即，网孔电流法
❖ END
推导回路电流方程：
a
i1
i2
i3
R1
R2
R3
+ uS1
il1uS2 +
il2
–
–
+ uS3 –
b
对回路列KVL， 用回路电流替代
支路电流
回路电 流方程
支路电流与回路电 流关系
i1 il1 i2 il1 il 2
i3 il 2
KVL：
R1i1 R2i2 uS 2 uS1 0
R2i2 R3i3 uS3 uS 2 0
解I优点： 不用背公式 分析过程可以不写

将 ud = u2 = R2(il1 – il2) 代入上式，整理得：
返回 上页 下页
第3章 电阻电路的分析方法
例10
R1
－ uS2＋
iS1
＋
i2 R3
il1
R2
u2 －
il2 ＋ uS3
－
il3
id il4
R4 ＋
ud
－
–R2il1 + (R2 + R3)il2 + R3il3 – R3il4 = uS2 – uS3
第3章 电阻电路的分析方法
3.4.2 回路电流法
网孔电流法 ★适用平面电路
回路电流法
★适用平面电路 ★适用非平面电路
◆网孔电流是在网孔中连续流动的假想电流 ◆回路电流是在回路中连续流动的假想电流
返回 上页 下页
第3章 电阻电路的分析方法
回路电流法
以回路电流为未知量列写电路方程进行电路 分析的方法叫做回路电流法。
－
il3
id il4
R4 ＋
ud
－
解 让iS1和 id都只有一个回路电流流过，前者为
il1、后者为il3，这样就不需要列回路1和回路3
的KVL方程。
返回 上页 下页
第3章 电阻电路的分析方法
例10
R1
－ uS2＋
iS1
＋
i2 R3
il1
R2
u2 －
il2 ＋ uS3
－
il3
id il4
R4 ＋
ud
R1
+ uS1
解 如图（b）所示，选择
支路4、5、6为树，
R2 Il1
R6
Il1
R5
R4

a i1 R1 uS1 + – il1 i2 R2 + –
uS2
推导回路电流方程： 推导回路电流方程： a i1 R1 uS1 + – il1 i2 R2 + – b i3 il2 R3 + uS3 – 支路电流 与回路电 流关系 i1 = il 1 i2 = il 1 − il 2 i3 = il 3 R1 i1 + R2 i2 = uS 1 − uS 2
对称阵， 对称阵，且 互电阻为负
用回路法求含有受控电压源电路的各支路电流。 受控电压源电路的各支路电流 例2. 用回路法求含有受控电压源电路的各支路电流。 1Ω 2Ω Ω Ω VCVS看作独立源建立方程 看作独立源建立方程； ① 将VCVS看作独立源建立方程； I1 2V + _ − I3 3Ω U2 Ω Ia Ib + I2 I4 1Ω Ω + Ic 3U2 –
Ia=1.19A Ib=0.92A Ic=-0.51A -
I1= Ia=1.19A, I2= Ia- Ib=0.27A, I3= Ib=0.92A, I4= Ib- Ic=1.43A, I5= Ic=–0.52A. * 由于含受控源，方程的系数矩阵一般不对称。 由于含受控源，方程的系数矩阵一般不对称。
方法2：选取独立回路时， 理想电流源支路仅 方法 ：选取独立回路时，使理想电流源支路仅仅 属于一个回路, 属于一个回路 该回路电流即 IS 。 R3 _ Ui + US1_ R1 I1=IS -R2I1+(R2+R4+R5)I2+R5I3=-US2 R1I1+R5I2+(R1+R3+R5)I3=US1 + I3 R4 I2 R5

K
u k ( t ) 0 或
u降 u升 或 uR US
k 1
式中 uk(t) 为该回路中第 k 条支路电压，K 为该回路处的支路数
示例
R2 i2
+ US_1
+ u2 _ +
R1 i1
+ _u1
_u3 _ u4 +
_ US4+ R4 i4
R3 i3
① 标定各元件电压、电流参考方向 ② 选定回路绕行方向，顺时针或逆时针 顺时针
小结 · 分析电路前必须选定电压和电流的参考方向
· 参考方向一经选定，必须在图中相应位置标注 （包括方向和符号）， 在计算过程中不得任意改变。
· 参考方向也称为假定正方向，以后讨论均在参考方向下进行，不考虑 实际方向。
· 电路中电位参考点可任意选择，参考点一经选定，电路中各点的电位
值就是唯一的，当选择不同的电位参考点时，电路中各点电位值将
Lumped parameter element
集总条件 实际电路的尺寸远小于使用时其最高工作频率所对应的
波长 d
注意
• 采用集总电路模型意味着不考虑电路中电场与磁场的相互作用， 不考虑电磁波的传播现象，认为电能的传送是瞬时完成的
• 集总假设为本课程的基本假设，以后所述的电路基本定律、定理 等均是以该假设为前提成立的
_
R1
+ US2
_
R2
b=3
n=2
R3
l=3
m=2
精品课件
22
2. 基尔霍夫电流定律 （KCL）
在集总参数电路中，任意时刻，对任意节点流出或流入该节点电流的代数 和等于零。
K
ik (t) 0

u1 R1i1
受控电压源先当作独立电压源列方程， 然后附加一个用回路电流表示控制量的方程 思考：控制量是电流和电压有什么不同？
含独立电流源
R1
R3
R2
R5
uS 1
iS
R4
uS 2
含独立电流源的处理方法-方法1
R1
R3
R2
R5
R4
uS 1
i1
iS
i2
i3
uS 2
u
回路1: (R1 R2 )i1 R2i2 us u
10
10
回路1: (10 20 20)i1 20i2 20i3 40
40V
i1
20 i2
20V 回路2 : - 20i1 (20 10 5)i2 5i3 20
20 i3
5
40
10V
按图示回路绕向列写回路电流方程
回路3: - 20i1 5i2 (20 5 40)i3 10
自阻取“+”
互阻正负取决于相邻回路电流在互 阻上的方向：相同取“+”，相反取 “-”
右端电源电压项：与回路电流关联 则“-”，非关联则“+”
含受控电压源
R1
R2
u1
uS
i1
R3 i2
50u1
含受控电压源的处理方法
R1
R2
u1
回路1: (R1 R3)i1 R3i2 us
uS
i1
R3 i2
50u1 回路2 : R3i1 (R2 R3)i2 50u1
到底该列多少个方程？
1. 如果既没有受控源，也没有电流源，那么有多少 个独立回路就列多少个回路电流方程。
2. 如果有受控源或电流源要视具体的电路和所用的 方法而定。

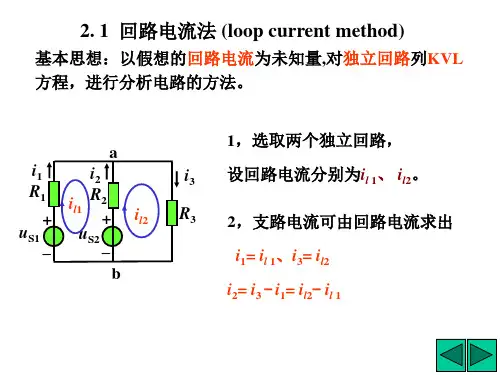
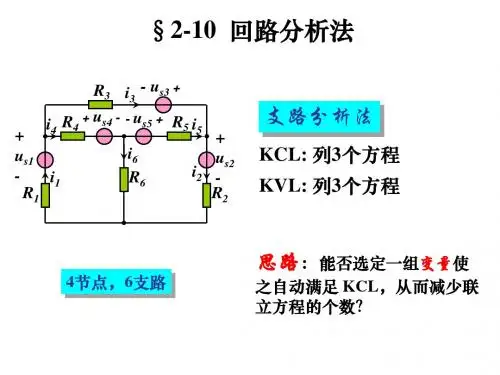
回路电流法的灵活应用回路电流法的灵活应用回路电流法的灵活应用回路电流法也是电路的系统分析方法之一．回路电流法的本质就是先利用 KCL 定理减少未知量的数目，然后只列 KVL 方程。

当电路的节点数较多，回路数较少时，采用画路电流法较为简单，因为列的方程数较少。

特别是当有理想电流源串连在支路中时，只要灵活应用回路电流法，便 _ 口丁以进一步减少昕列的 KVI 方程数。

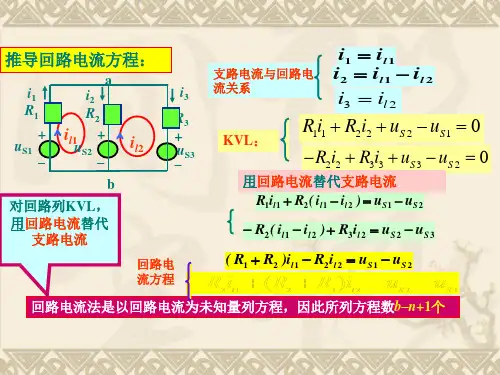
图 1 中有 3 个独立回路 ( 也即网孔 ) ，选取 3 个独立回路的回路电流为未知量，图中选取的是网孔，未知当有一理想电流源串联在支路中时，独立回路选取的原则是让理想电流源所在的支路在且仅在一个选取的独立回路中，这样理想电流源支路只有一个回路电流流过，该回路电流即为理想电流源的值，是已知的，这样未知量便少一个，所需列的 KVL 方程也可以少一个，选哪些回路列 KVL 方程呢 ? 因为电流源两端的电压与该元件本身无关，是由外电路决定的．故无法用设置的未知量表达其两端的电压，所以列KVL 方程时，要避开有理想电流源的独立回路来列 KVL 方程。

图 2 中同样有 3 个独立回路，理想电压源 Is 直接串联在支路中，选取独立回路时，先满足让理想电流源 Is所在支路在一个独立回路中 ( 图中的回路 1) ，该电路有 3 个独立回路，故还需选取两个回路，为满足让理想电流源支路仅在一个独立回路中，剩余的回路去掉电流源支路来选取，如图 2 中的回路 2 画路电流为 I2 与画路 3 回路电流为 I3 ，这样选好回路以后回路电流 I1=IS 为已知的，只需列回路 2 与回路 3 的 KVL 方程图 3 有两个理想电流源串联在支路中，独立回路数 3 个，恰当选取独立回路，即：让理想电流源所在的支路 ( 且仅在一个独立回路 ) 中。

可以只列一个 KVL 方程．选回路时，先让 ls1在回路 1 中，回路电流为 I1 ，第二步去掉 ls1 所在支路来选取独立回路， Is2 在回路 2 中，让画路电流为 I2 ，第三步去掉 Ist 与 Is2 所在支路，剩下的回路 3为所选取的第三个独立回路，回路电流为 I3 ，这样确保 iS1 支路与 Is2 支路在且仅在一个独立回路中，因此回路 I 的回路电流 I1=Is1 为已知的，回路 2 的回路电流I2=Is2 也为已知的，只需列回路 3 的 KVL 方程为：回路电流法回路电流法是以一组独立回路电流作为变量列写电路方程求解电路变量的方法。

由同名端及u、i参考方向确定互感线圈的特性方程
有了同名端，以后表示两个线圈相互作用，就不再考虑实际绕向，而只画 出同名端及参考方向即可。
M
*
*
i1
+ u21 –
M
*
*
i1
– u21 +
u21
M
di1 dt
u21
M
di1 dt
例
i1
M
i2
+*
*+
u1 L1 _
L2 u2 _
u1
L1
di1 dt
M
di2 dt
u
L1
L2
–
i1
M
i2
+
**
+
u
L1
L2
u
–
–
•
I
jM
j(L1－M)
•
•
I1 I2
j(L2－M)
•
I1
j(L1－M)
•
I2
j(L2－M)
jM
4. 受控源等效电路
i1
M
i2
+
**
+
u
L1
L2 u
–
–
•
I1
+
j L1
•
U1
+
•
jM
–
I–2
•
I2
+
j L2
•
+
U2
•
jMI 1
–
–
•
•
•
U 1 jL1 I 1 jM I 2
US
j (L1 L3 2M31)

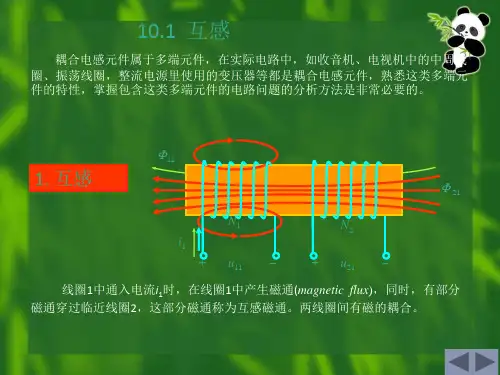
回路电流法
回路电流法，也称为基尔霍夫第二定律，是电路分析中常
用的一种方法。

它基于基尔霍夫电流定律，即在一个电路中，电流在节点处的总和为零。

回路电流法的基本原理是，将电路分解为若干个回路，在
每个回路中，假设一个未知的电流方向，然后根据基尔霍
夫第二定律，在每个节点处列出方程，解方程组得到未知
电流的值。

具体步骤如下：
1. 将电路分解为若干个回路，选择一个回路作为参考回路。

2. 对每个回路，假设一个未知电流方向，并定义电流的正
方向。

3. 对每个节点，根据基尔霍夫第二定律，列方程。

对于每
个节点，电流进入节点的总和等于电流离开节点的总和。

4. 解方程组，得到未知电流的值。

通过回路电流法，可以得到电路中各个分支的电流大小和
方向，从而可以求解电路中的各种参数，如电压和功率等。

需要注意的是，回路电流法只适用于直流电路或稳态交流
电路，且要求电路是线性的。

教后记
教学程序
教学内容
教学方法与
教学手段
[练习]
解：假设回路电流I11、I22和I33，方向如图中所示。
根据基尔霍夫电压定律列出回路电压方程式
I11（R1+R3）- I22R3= E1
I22（R3+R4+R5）- I11R3+ I33R4= 0
I33（R2+R4）+ I22R4= E2
代入数据得
25I11– 20I22– 45 = 0
代入已知量，得
I11 （8+15+2）+I22 15=60
I22 （15+15+5）+I11 15=10
所以I11= 3A I22= -1A
I1=I11=3A方向同I11
I2= -I22= 1A方向与I22相反
I3=I11+I22=2A方向同I11
回路电流法：用于支路较多而回路较少的电路。
P. 66 5
P．66
6．在图所示的电路中，已知E1=60V，E2=10V，r1=2Ω,r2=5Ω,R1=8Ω,R2=R3=15Ω，用回路电流法求各支路上的电流。
教后记
教学程序
教学内容
教学方法与
教学手段
小结：
作业：
解：设回路电流方向如图所示，
I11 （R1+R3+r1）+I22R3=E1
I22 （R2+R3+r2）+I1142I33= 0
45I33+ 42I22– 48 = 0
所以I11= 1A I22= - 1A I33= 2A
由此即可确定各支路中的电流分别是
I1= 1A I2= 2A I3= I11– I22= 2A

4.2网孔电流法的一般步骤
(1) 选定电路中各个网孔的绕行方向；
(2) 对m个网孔，以网孔电流为未知量，列写其KVL方程； (3) 求解上述方程，得到m个网孔电流； (4) 求各支路电流（用网孔电流表示）； (5) 结果验证。
例6. 用网孔电流法求各支路电流。 I1 R1 + US1 _ I2 R2 Im1 + US2 _ I3 Im2
从上式中可知，对单连支回路来说，连支电流就是回路 电流，树支电流可以通过连支电流或回路电流表示，即全部 支路电流可以通过回路电流表示。
5.2回路电流方程
对于具有b条支路、n个结点的电路，回路电流方程的
一般形式为（独立回路数l = b - n + 1）：
R11il1 + R12il 2 + + R1l ill = uS11 R21il1 + R22il 2 + + R2l ill = uS22 Rl1il1 + Rl 2il 2 + + Rll ill = uSll 其中 Rkk：自电阻(总为正) ，k = 1，… ，l ( 任选绕行方向)。
Rjk： 互电阻
流过互阻的两回路电流方向相同，则 Rjk前面取正号
流过互阻的两回路电流方向相反，则 Rjk前面取负号
两个回路之间没有公共支路或虽有公共支路但其电 阻为零时，Rjk = 0
5.2回路电流方程
R11il1 + R12il 2 + + R1l ill R21il1 + R22il 2 + + R2l ill Rl1il1 + Rl 2il 2 + + Rll ill = uS11 = uS22 = uSll

3Ω
i6 1Ω il2
+
i2
14V -

il1

(1
2

2) il2

2il3

2 14
2Ω 6il1 2il2 3 2 6il3 6 2 2
i1 il1 3 A i2 il2 1A i3 il3 2 A
i4 il1 il3 1A
R3 i3 - us3 +
+ i4 R4 + us4 - -ilu3s5 + R5 i5 +
us1
R1
i1
il1
i6 R6 il2
i2
us2 -
R2
R11、R22 、R33分别是回路1、2、3的各支路电阻之和，并分别
称为回路1、2、3的自电阻(self resistance)；
自电阻前的符号为正
I4 = I1+I2 =(154) A = 11 A I5 = I1+I3 =(15+2) A = 17 A I6 = I3-I2 =(2+4) A = 6 A
解法二：选取回路电流如图所示
I1 = 15 A
I3

1 9Ux
(1 2 3)I4
3 Ux 9
(1 3)15
0
补充方程
i2=il2
i3=il3
i4=il1-il3 i5=il2-il3 i6=-il1-il2
i i4 i5 i6
(il1 il3 ) il 2 il 3 il1 il 2
0
il1、 il2、 il3自动满足KCL 是一组完备的独立变量

•网孔电流经过的各条支路，若某支路上仅流过一个网孔电 流，且方向与网孔电流一致时，则这条支路电流在数值上应 等于该网孔电流，若方向相反应为回路电流的负值；若某公 共支路上通过两个网孔电流时，则支路电流在数值上应等于 这两个网孔电流之代数和，其中与该支路电流方向一致的网 孔电流取正值，与该支路电流方向相反的网孔电流取负值。
求各元件上吸收的功率，进行功率平衡校验
R1上吸收的功率为：PR1=62×7=252W R2上吸收的功率为：PR2=(－2)2×11=44W R3上吸收的功率为：PR3=42×7=112W US1上吸收的功率为：PS1=－(6×70)=－420W 发出功率 US2上吸收的功率为：PS2=－(－2)×6=12W 吸收功率 元件上吸收的总功率：P=252+44+112+12=420W
电路分析基础
第2章 电路的基本分析方法
2.1 支路 电流法
2.2 回路 电流法
2.3 结点 电压法
2.5 戴维南 定理
2.4 叠加 定理
返章目录
本章的学习目的和要求
熟练掌握支路电流法，因为它是直接应 用基尔霍夫定律求解电路的最基本方法之一； 理解回路电流及结点电压的概念，掌握回路电 流法和结点电压法的内容及其正确运用；深刻 理解线性电路的叠加性，了解叠加定理的适用 范围；理解有源二端网络和无源二端网络的概 念及其求解步骤，初步学会应用维南定理分析 电路的方法。
• 应用KCL列写n-1个独立结点方程式。
• 应用KVL列写m-n+1个独立电压方程式。 • 联立求解方程式组，求出m个支路电流。
支路电流法应用举例
• 举例一
用支路电流法求解下图所求电路中各支路电流，并用功
率平衡校验求解结果。

选择③为参考节点；
节点电压：u1，u2； u1, u2自动满足KVL
（电位单值性） 是一组完备的独立变量。
+ us1 - R1 i1
R3 1
i2 R2
3
i3
2 i5
i4
R5
R4
+
us2
-
电路原理
§2-10 回路分析法·回路电流
回路分析法
关键：回路电流
+ us1 - R1 i1
il1 R3
i3
2 i5
回路中独占支路的电流就为该回路的回路电流；
回路共有支路的电流就为流过该支路的回路电流
i4 R4 il3
R5
+ us2
-
叠加。
方向：指定的回路电流参考方向
3
(独立)回路电流数＝支路数-节点数+1=支路数-独立节点数
求解3个变量 列写3个独立方程 ?
电路原理
§2-10 回路分析法 ·回路电流 + us1 - R1 i1
+ us1 - R1 i1
il1 R3 1
(R1 R3 )il1 R3il2 us1
i2
il2
R2
R3il1 (R2 R3 R4 )il2 R4il3 0
i3
2 i5
i4 R4 il3
R5
+ us2
-
R4il2 (R4 R5 )il3 us2
3
电路原理
§2-10 回路分析法 ·物理意义
1
KVL：ub 0
(b-n+1)个
i2
il2
R2
i4 R4 il3
R5
+ us2
-

−Ri1 + (R + R2 )i2 = U 1 1
−R4i1 + (R + R4 )i3 = − U 3
RS + US _ R1 R2 电流源看作电 压源列方程
i1
R4
iS i2
+ _ U
增补方程： 增补方程：
i3 R 3
iS = i2 − i3
电路 选取独立回路，使理想电流源支路仅仅属于一个 选取独立回路， 回路, 回路, 该回路电流即 IS 。 例
(uA-uB)+uB-uA=0
KVL自动满足 iS3
uA
uB
1 i1 iS1 R1
实例
选定参考结点， 选定参考结点， 标明其余n-1个独立 结点的电压
i2 R 2 2 R4
i3 R3 i4 R5 + uS _
3 i5
方程： 列KCL方程：
iS2 1 i1 iS1 R1 i2 R 2 2 R4 i3 R3 i4
电路
例
RS + US _
R1
i1
+ R4
i2 i3 5U
R2 _ + R3 U _
增补方程： 增补方程：
U = R i3 3
(RS + R + R4 )i1 − Ri2 − R4i3 = US 1 1 −Ri1 + (R + R2 )i2 = 5 U 1 1
−R4i1 + (R + R4 )i3 = −5 U 3
电路
3.5 回路电流法
以基本回路为独立回路， 以基本回路为独立回路， 以独立回路电流 连支电流）为变量列方程。 回路电流（ 以独立回路电流（连支电流）为变量列方程。 是网孔电流法的推广， 是网孔电流法的推广，不再仅适用于平面电路

例2 列写下图含VCCS电路的节点电压方程。
解： (1) 先把受控源
1
R2 2
当作独立源看
(2) 用节点电压 表示控制量。
iS1
R1 R
+ uR2 _ R3
11
1
( R1
R2
)U n1
R2
Un2
iS1
1 R2
Un1
( 1 R3
1 R2
)U n 2
gmuR2
uR2 Un1 Un2
G12 G21
例1 用节点法列写以UA、 UB为节点电压的方程。
G1 UA
G2 UB G3
+US1
G4 IS
G5
+US2
解： 电路可改画为 G1 UA G2 UB G3
US1
G4 IS
G5
US2
G1 UA G2 UB G3
US1
G4 IS
G5
US2
列节点电压方程：
(G1 G4 G2 )UA G2UB IS G1US1 G2UA (G2 G3 G5 )UB IS G3US2
R12= -R2 ， R21= -R2 代表回路1和回路2的公共电阻（互电阻）
uSl1= uS1-uS2 回路1中所有电压源电压升的代数和
uSl2= uS2 回路2中所有电压源电压升的代数和
一般情况，对于具有 l=b-(n-1) 个回路的电路，有
R11i1+R12i2+ …+R1l il=uSl1
回路电流法：以回路电流为未知量列写电路方程分析电路
的方法。
a
i1
i2
i3
R1
R2
+ il1 + il2

回路电流法
1、基本的回路电流 法
1、已知右图电路结构，其中中电阻的单位为欧姆。 求：R4中的电流I=？
分析：该电路是具有3个独立回路的电路, 无电流源和受控电源, 可在选 取独立回路的基础上直接列出标准的回路方程求解，方程左、右的规 律由KVL决定，选独立回路的方法不限。本题可选取网孔为独立回路
解：
本题采规用虚回假路的回电路电流流法法。列出标准方程，一般采用虚假的回
(15+10)I1+10I2-10I3=-3U1
(2+4+6路)I1-电6I2=流16-法48+，32 即设包含有电流源的电流为回路电流； -（8I注1+意(或2:选+8增择+4自0加)I然2-网4电0孔I3流作=为13源独6 立两回端路,已的标电于图压中）为独立变量，再按KVL
R3
已分知析电 ：列路该结电出构路独如中右含立，有其理回中想路电电阻流的单源位，电为不流欧能姆用方。常 程进行求解。本题采用前 1、基本者的进回路行电流求法解，独立回路的选择方法已标在图上。
U S1
2、含有无伴电流源的回路电流法
已知电路结构如右，其中电阻单位为欧姆。
解： 者进行求解，独立回路的选择方法已标在图上。
解得：U1=30V
*注意:独立回路的选择方法 不同于前面两个题目。
2、含有无伴电流源的回路电流法
已知电路结构如右，其中电阻单位为欧姆。
3、含有求受：控源电的回压路U电0流。法
1、已知右图电路结构，其中中电阻的单位为欧姆。
1-1、0I已1-(知2+右3+图10电分)I路2 +结析(1构0：+，1+其该2+中3)中电I3电=3路阻U1的中单位含为有欧姆理。想电流源，不能用常