拓展资源：分层练习

分层作业练习题在学习过程中，分层作业练习题是一种有效的学习工具，它可以帮助学生巩固所学知识，检验他们的理解和应用能力，并提供个性化的学习反馈。

本文将探讨分层作业练习题的定义、优势以及如何有效设计和使用这些练习题。

一、分层作业练习题的定义分层作业练习题是指针对不同学生水平和能力的练习题集。

这些题目根据学生的理解和应用能力被分为不同的层次或难度。

通过这种方式，学生可以选择适合自己水平的题目进行练习，提高学习效果。

二、分层作业练习题的优势1. 个性化学习：分层作业练习题允许学生根据自己的能力水平选择适合自己的题目进行练习，帮助他们更好地理解和应用所学知识。

2. 激发兴趣：通过提供不同层次和类型的练习题，学生可以选择自己感兴趣或有挑战性的题目，激发他们的学习兴趣。

3. 个性化反馈: 分层作业练习题可以为学生提供个性化的学习反馈，帮助他们了解自己的学习情况，发现自己的不足，并有针对性地进行学习和提高。

三、如何设计和使用分层作业练习题1. 明确学习目标：在设计分层作业练习题之前，教师需要明确学习目标，确定所要教授的知识和技能，并根据学生的水平和能力进行细分。

2. 分层设计：根据学生的水平和能力，将练习题分为不同的层次或难度。

每个层次的题目应该有适当的挑战性，既能够保持学生的兴趣，又不会让学生感到过于困难。

3. 提供选择：教师应该向学生提供多个不同难度和类型的练习题，让学生根据自己的能力和兴趣进行选择。

这样可以满足学生的个性化需求，并激发他们的学习动力。

4. 反馈与指导：学生完成练习题后，教师应该及时给予个性化的学习反馈，并提供必要的指导。

这样可以帮助学生更好地理解和应用所学知识，纠正错误，提高学习效果。

5. 管理和评估：教师需要合理安排和管理学生的分层作业练习，确保学生按时完成，并及时对学生的练习情况进行评估。

这样可以及时发现学生的学习进步和困难，调整教学策略。

总结：分层作业练习题是一种有益于学生学习的工具，它可以个性化地满足学生的需求，提供挑战和反馈，并激发学生的学习动力。

四年级数学课堂作业分层练习题作为四年级学生，在数学课上，我们经常需要通过课堂作业来巩固和提高自己的数学能力。

这就意味着我们需要有一个有效的方法来划分和分类练习题，以便我们能够有针对性地进行练习。

在本文中，我将介绍一种常用的方法——分层练习题法，来帮助四年级学生更好地完成数学课堂作业。

一、基础练习题层基础练习题层是数学课堂作业的第一层，它主要涵盖了四年级数学课程的基本概念和操作。

在这一层中，我们将遇到一些简单而基础的练习题，例如四则运算、数学公式的应用和简单的几何图形等。

这些题目旨在培养我们的计算能力和逻辑思维能力，帮助我们建立数学基础。

二、拓展练习题层拓展练习题层是数学课堂作业的第二层，它在基础练习题层的基础上，进一步提高了题目的难度和复杂程度。

在这一层中，我们将遇到一些需要运用多种数学知识和技巧解决的问题，例如应用题、成大问题和逻辑推理等。

这些题目旨在激发我们的创造力和思维能力，培养我们解决实际问题的能力。

三、拔高练习题层拔高练习题层是数学课堂作业的第三层，它是整个练习题的高难度部分。

在这一层中，我们将遇到一些复杂而抽象的数学问题，例如多步运算题、复杂的几何图形问题和数学证明等。

这些题目旨在挑战我们的智力和推理能力，培养我们解决复杂问题的能力。

总结：通过分层练习题法，四年级学生可以根据自己的数学水平和能力来有针对性地进行数学课堂作业。

基础练习题层可以帮助我们打牢数学基础，拓展练习题层可以提高我们的综合能力，拔高练习题层可以培养我们的智力和解决问题的能力。

因此，四年级学生在完成数学课堂作业时，可以根据题目的难度来合理划分和分类练习题，选择适合自己的练习题层次，通过有计划地练习，提高数学学习效果。

总结起来，四年级数学课堂作业的分层练习题法可以让我们有条不紊地提高数学水平，帮助我们更好地理解和掌握数学知识。

我们应该认真对待每一道题目，勤于思考和动手实践，相信通过不断地努力，我们一定会在数学学习中取得更大的进步！。

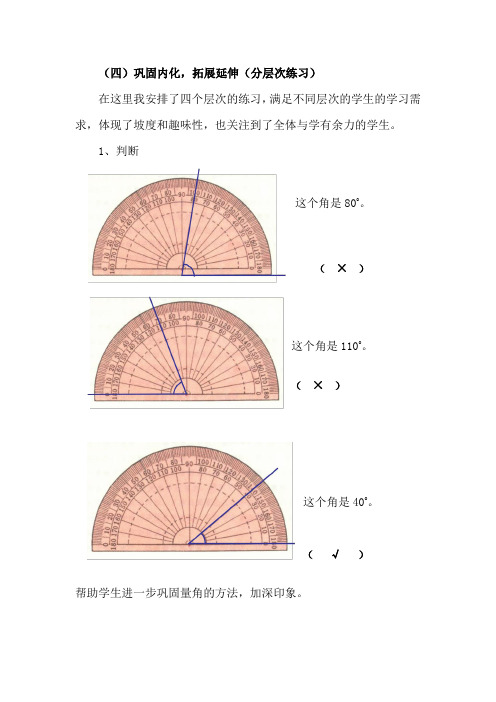
（四）巩固内化，拓展延伸（分层次练习）在这里我安排了四个层次的练习，满足不同层次的学生的学习需求，体现了坡度和趣味性，也关注到了全体与学有余力的学生。

1、判断这个角是80o。

（×）这个角是110o。

（×）这个角是40o。

（√）帮助学生进一步巩固量角的方法，加深印象。

2、先比较每组角中哪个角大，再进行测量，说说你发现了什么。

（1） 边长相等，角的大小不等。

（2）边长不等，角的大小相等。

学生独立完成，教师可以投影演示量角过程，不仅可以巩固量角的方法，而且借助量角练习，复习巩固了二年级已经认知的角的大小与边的长短无关，与两边叉开的大小有关。

3、小明已经将角的顶点和量角器的中心点对齐，你能猜出下面两个角的度数吗？（ 30o）o )(o第一道题，由于角的两边都有露出的部分，所以学生可以毫不犹豫的说出是30o 。

第二道题学生会产生分歧，有些学生会发现图中遮挡住了角的一条边，无法判断角的度数。

在这里我预设了三种情况，一种是角的一条边与内刻度的0o 刻度线重合，得出的角是70o ；一种是角的一条边与外刻度线的0o 刻度线重合，得出的角是70o ；第三种是角的边不与0o 刻度线重合，那么我们可以利用数格的方式进行量角计算。

由此可想到许多种可能，所以这道题答案是不唯一的。

通过这项练习，再一次巩固学生对测量及读数方法的掌握，加深了对量角器的认知程度，提升了自己的思维模式。

4、这道题可以作为一个课堂反馈练习，并且提升难度，让学生感知什么是对顶角。

发现：两条直线相交，相邻的两个角的度数相加的和都等于180°，对顶角大小相等。

拓展资源：分层练习根据本校学生及教学情况，可在教学过程中，选择以下内容进行补充或拓展基础训练① 为了拓展销路，商店对某种照相机的售价了调整，按原价的8折出售，此时的利润率为14%，若此种照相机的进价为1200元，问该照相机的原售价为多少元？ 1710元② 某种商品进价为a 元，商店将价格提高30％作零售价销售，在销售旺季过后，商店又以8折（即售价的80％）的价格开展促销活动.这时一件商品的售价为 （ C ）A. a 元B. a 8.0元C. a 04.1元D. a 92.0元提高训练③ 新年来临爸爸想送Ｍike 一个书包和随身听作为新年礼物．爸爸对Ｍike 说：“我在家乐福、人民商场都发现同款的随身听的单价相同，书包单价也相同，随身听和书包单价之和是452元，且随身听的单价比书包单价的4倍少8元，你能说出随身听和书包单价各是多少元，那么我就买给你做新年礼物”。

你能帮助他吗？（1）解：设书包单价为x 元，则随身听单价为y 元,根据题意可列出方程：⎩⎨⎧=-=+.84,452y x y x 解之得：⎩⎨⎧==.360,92y x 答：书包单价92元，随身听单价360元。

最优化决策：聪明的Mike 想了想回答正确后便同爸爸去买礼物，恰好赶上商家促销，人民商场所有商品打八折销售，家乐福全场购物满100元返购物券30元销售（不足100元不返券，购物券全场通用），但他只带了400元钱，如果他只在一家购买看中的这两样物品，你能帮助他选择在哪一家购买吗？若两家都可以选择，在哪一家购买更省钱？提示：书包单价92元，随身听单价360元。

（2）在人民商场购买随声听与书包各一样需花费现金452×108=361.6（元） ∵ 361.6<400 ∴可以选择在人民商场购买。

在家乐福可先花现金360元购买随身听，再利用得到的90元返券，加上2元现金购买书包，共花现金360+2=362（元）。

因为362＜400，所以也可以选择在家乐福购买。

第五单元：三角形第2课时：三角形的分类班级：姓名: 等级:【基础训练】一、选择题。

1.直角三角形也可以是（）。

A. 等腰三角形B. 等边三角形C. 钝角三角形2.一个钝角三角形，它也可能是（）。

A. 有一个直角B. 三条边相等C. 有两条边相等3.下面四位同学的说法中，正确的是（）。

A. 等腰三角形一定是锐角三角形。

B. 小月班同学的平均体重36千克，小飞班同学的平均体重38.5千克，小月的体重不一定比小飞轻。

C. 三角形3个内角的度数之和等于一个周角的度数。

D. 直角三角形只有一条高。

4.下图中的三角形都被长方形遮住了一部分，其中一定为锐角三角形的是( )。

A. B. C. D.5.在一个三角形里，如果最大的内角是100°，这个三角形一定是（）A. 锐角三角形B. 直角三角形C. 钝角三角形二、判断题。

6.三角形按边分为等边三角形和锐角三角形。

（）7.顶角是60度的等腰三角形一定是等边三角形。

（）8.如果一个三角形的三个内角的度数比为1：2：3，那么这个三角形一定是直角三角形。

（）9.等边三角形的每一个内角都是60°。

（）10.一个三角形中最大的角是钝角，这个三角形一定是钝角三角形。

（）三、填空题。

11.在一个三角形中，两个角分别是65度和40度，那么第三个角的度数是________度，这是一个________三角形。

12.一个三角形中最少有________个锐角，最多有________个钝角。

【拓展运用】13.下面是三块三角形玻璃打碎后留下的碎片，你能判断出它们原来各是什么三角形吗？参考答案1.【答案】A2.【答案】C3.【答案】B4.【答案】D5.【答案】C6.【答案】错误7.【答案】正确8.【答案】正确9.【答案】正确10.【答案】正确11.【答案】75；锐角12.【答案】2；113.【答案】解：图一中打碎的那个角的度数是180°-30°-40°=110°，所以这个三角形原来是钝角三角形；图二中打碎的那个角的度数是180°-60°-60°=60°，所以这个三角形原来是锐角三角形；图三中打碎的那个角的度数是180°-50°-40°=90°，所以这个三角形原来是直角三角形。

部编版⼩学语⽂四年级语⽂有效作业分层练习（拓展）公开课教案四年级语⽂第⼀单元学校班别姓名⼀、⽐⼀⽐，然后选择恰当的词语填空。

观赏欣赏玩赏赞赏1、我静静地（）着优美的交响乐曲。

2、中外游客不约⽽同地来到令⼈神往的九寨沟，（）那美丽的⼭⽔。

3、⼤家（）着同学们亲⼿制作的飞机、轮船、汽车模型。

4、这次活动给⼤家留下了深刻的印象，赢得了⼤家的（）。

⼆、句式练习1、照样⼦写句⼦。

（1）例：漓江的⽔真静。

漓江的⽔真静啊，静得让你感觉不到它在流动。

花坛真漂亮。

（2）溪流时⽽宽，时⽽窄，时⽽缓，时⽽急，溪声也时时变换调⼦。

（3）桂林的⼭真秀啊，像翠绿的屏障，像新⽣的⽵笋，⾊彩明丽，倒映⽔中。

三．补充诗句，并在诗句后⾯的括号内写出诗句所描写的季节。

（1）⼩河才露尖尖⾓，（）。

（）（2）孤⾈蓑笠翁，（）。

（）（3）停车坐爱枫林晚，（）。

（）（4）碧⽟妆成⼀树⾼，（）。

（）南开实验学校有效作业分层练习（拓展）四年级语⽂第⼆单元学校班别姓名给我⼀个承诺故事发⽣在美国的得克萨斯州。

⼀个风雪交加的夜晚，⼀位名叫克雷斯的年轻⼈因为汽车“抛锚”被困在郊外。

正当他万分焦急的时候，有⼀位骑马的男⼦正巧路过这⾥。

见此情景，这位男⼦⼆话没说，使⽤马帮助克雷斯把汽车拉到了⼩镇上。

事后，当感激不尽的克雷斯拿出⼀沓美钞（chāo）对他表⽰酬谢时，这位男⼦说：“这不需要回报，但我要你给我⼀个承诺，当别⼈有困难的时候，你也要尽⼒帮助他。

”于是，在后来的⽇⼦⾥，克雷斯主动帮助了许许多多的⼈，并且每次都没有忘记转述那句同样的话给所有被他帮助过的⼈。

⼏年后的⼀天，克雷斯被突然暴发的洪⽔困在了⼀个孤岛上，⼀位勇敢的少年冒着被洪⽔吞没的危险救了他。

当他感谢少年的时候，少年竟然也说出了那句克雷斯曾说过⽆数次的话。

“我不需要回报，但我要你给我⼀个承诺……”克雷斯的胸中顿时涌起了⼀股暖流。

爱⼼是不需要回报的，但爱⼼是可以传递的。

如果说，每⼀件善事都是⼀颗珍珠的话，那么我们每⼀个⼈都可以是⼀条⾦线。

拓展资源：分层练习根据本校学生及教学情况可在教学过程中，选择以下内容进行补充或拓展。

基础训练1．某医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y （微克）随时间x （时）的变化情况如图所示，当成人按规定剂量服药后，（1）服药后 时，血液中含药量最高，达每毫升微克，接着逐步衰减；（2）服药5时，血液中含药量为每毫升 微克；（3）当x ≤2时，y 与x 之间的函数关系式是 ； （4）当x ≥2时，y 与x 之间的函数关系式是 ；（5）如果每毫升血液中含药量3微克或3微克以上时，治疗疾病最有效，那么这个有效时间范围是 ．2．如图，AB OB ,分别表示甲、乙两人的运动图象，请根据图象回答下列问题：（1）如果用t 表示时间，s 表示路程，那么甲、乙两人各自的路程与时间的函数关系式是甲： ，乙： ；（2）甲的运动速度是 千米/时；（3）两人同时出发，相遇时，甲比乙多走 千米． 提高训练1、观察甲、乙两图，解答下列问题（1）填空：两图中的（ ）图比较符合传统寓言故事《龟免赛跑》中所描述的情节．（2）根据1中所填答案的图象填写下表：265432y/微克x/时O26542015105t/小时s/千米BA O（3）根据1中所填答案求：○1龟免赛跑过程中的函数关系式（要注明各函数的自变量的取值范围）；○2乌龟经过多长时间追上了免子，追及地距起点有多远的路程？2、某电视机厂要印刷产品宣传材料，甲印刷厂提出：每份材料收1元印刷费，另收1500元制版费；乙印刷厂提出：每份材料收2.5元印刷费，不收制版费．（1）分别写出两厂的收费y （元）与印制数量x （份）之间的关系式； （2）在同一直角坐标系内作出它们的图象； （3）根据图象回答下列问题：① 印制800份宣传材料时，选择哪家印刷厂比较合算？② 电视机厂拟拿出3000元用于印刷宣传材料，找哪家印刷厂印刷宣传材料能多些？3、生态公园计划在园内的坡地上造一片有A B ，两种树的混合林，需要购买这两种树苗2000棵．种植A B ，两种树苗的相关信息如下表：设购买A 种树苗x 棵，造这片林的总费用为y 元．解答下列问题：（1）写出y （元）与x （棵）之间的函数关系式；（2）假设这批树苗种植后成活1960棵，则造这片林的总费用需多少元？4、如图，l A 与 l B 分别表示A 步行与B 骑车同一路上行驶的路程S 与时间t 的关系． （1）B 出发时与A 相距多少千米？（2）走了一段路后，自行车发生故障，进行修理，所用的时间是多少小时？ （3）B 出发后经过多少小时与A 相遇？（4）若B 的自行车不发生故障，保持出发时的速度前进，那么经 过多少时间与A 相遇？相遇点离B 的出发点多远？你能用哪些方法 解决这个问题？在图中表示出这个相遇点C ．视野拓展抗震救灾中，某县粮食局为了保证库存粮食的安全，决定将甲、乙两个仓库的粮食，全部转移到具有较强抗震功能的A ,B 两仓库。

本文由顾梓汐贡献 ｄｏｃ文档可能在ＷＡＰ端浏览体验不佳。

建议您优先选择ＴＸＴ，或下载源文件到本机查看。

部分分层拓展习题 进行分层训练，既满足了不同学生的需求，同时也便于教师及时地了解学生的情况．教　师可以根据学生的情况选择以下题目进行练习，也可留作家庭作业． 基础训练 １．为迎接新年的到来，同学们做了许多拉花布置教室，准备召开新年晚会，小刚搬来　一架高为　２．５　米的木梯，　准备把拉花挂到　２．４　米的墙上，　则梯脚与墙角的距离应为　２．如图，小张为测量校园内池塘　Ａ，Ｂ　两点的距离，他在池塘边选　定一点　Ｃ，使∠ＡＢＣ＝９０°，并测得　ＡＣ　长　２６ｍ，ＢＣ　长　２４ｍ，则　Ａ，Ｂ　两点间的距离为 Ａ　Ｃ　Ｂ 米． ｍ．　． ７　２５　ｃｍ． ３．如图，阴影部分是一个半圆，则阴影部分的面积为　（　π　不取近似值）　４．底边长为　１６ｃｍ，底边上的高为　６ｃｍ　的等腰三角形的腰长为 ５．一艘轮船以　１６ｋｍ／ｈ　的速度离开港口向东北方向航行，另一艘轮船同时离开港口以　１２ｋｍ／ｈ　的速度向东南方向航行，它们离开港口半小时后相距　ｋｍ． 提高训练 ６．一个长为　１０ｍ　为梯子斜靠在墙上，梯子的顶端距地面的垂直高度为　８ｍ，梯子的顶　端下滑　２ｍ　后，底端滑动　ｍ． Ｂ　Ａ　Ｃ　Ｄ ７．如图所示的图形中，所有的四边形都是正方形，所有的三角形都　是直角三角形，其中最大的正方形的边长为　７ｃｍ，则正方形　Ａ，Ｂ，Ｃ，Ｄ　的面积的和是　ｃｍ　． ２ ７ｃｍ ８．已知　Ｒｔ△ＡＢＣ　中，∠Ｃ＝９０°，若　ａ　＋　ｂ　＝　１４　ｃｍ，　ｃ　＝　１０　ｃｍ，则　Ｒｔ△ＡＢＣ　的面积　为（　）　．　（Ａ）２４ｃｍ２　（Ｂ）３６ｃｍ２　（Ｃ）４８ｃｍ２　（Ｄ）６０ｃｍ２ ９．如图，分别以直角三角形的三边为边长向外作正方形，然后分别以三个　正方形的中心为圆心，正方形边长的一半为半径作圆，记三个圆的面积分别为　Ｓ１，Ｓ２，Ｓ３，则　Ｓ１，Ｓ２，Ｓ３　之间的关系是（　（Ａ）　Ｓ１　＋　Ｓ　２　＞　Ｓ　３　（Ｃ）　Ｓ１　＋　Ｓ　２　＜　Ｓ　３　）　． Ｓ３　Ｓ２　Ｓ１ （Ｂ）　Ｓ１　＋　Ｓ　２　＝　Ｓ　３　（Ｄ）无法确定 １０．暑假中，小明和同学们到某海岛去探宝旅游，按照如图所示的　路线探宝．　他们登陆后先往东走　８ｋｍ，又往北走　２ｋｍ，遇到障碍后又往　西走　３ｋｍ，再折向北走　６ｋｍ　处往东一拐，仅走　１ｋｍ　就找到了宝藏，则　登陆点到埋宝藏点的直线距离为　ｋｍ． 登登埋　８ １ 埋埋埋埋 ６　３　２ 知识拓展 １１．如图，已知直角△ＡＢＣ　的两直角边分别为　６，８，分别以其三边为直径作半圆，求　图中阴影部分的面积． Ｃ　６　Ａ　８　Ｂ １２．如图，有一块直角三角形纸片，两直角边　ＡＣ＝６ｃｍ，ＢＣ＝８ｃｍ，现将直角边　ＡＣ　沿直线　ＡＤ　折叠，使它恰好落在斜边　ＡＢ　上，且与　ＡＥ　重合，求　ＣＤ　的长． Ａ　Ｅ　Ｂ Ｃ Ｄ１。

拓展资源：分层练习根据本班学生实际情况可在教学过程中选择下述内容补充或拓展.(1)基础训练1.下列函数中，是一次函数但不是正比例函数的是（ ）. A.3x y =- B.3y x =- C.12x y += D.2212x y x += 2.若函数23y x b =+-是正比例函数，则b = .3.某学生的家离学校2km ，他以16km/min 的速度骑车到学校，写出他与学校的距离s （km ）和骑车的时间t(min)的函数关系式为 ，s 是t 的 函数.(2)提高训练4.如图,在三角形ABC 中,∠B 与∠C 的平分线交于点P,设∠A=x ,∠BPC=y ,当∠A 变化时,求y 与x 之间的函数关系式,并判断y 是不是x 的一次函数.5.将长为13.5cm ，宽为8cm 的长方形白纸，按照图所示的方法粘合起来，粘合部分宽为1.5cm.（1）求5张白纸粘合后的长度；（2）设x 张白纸粘合后的总长度为y cm ，求y 与x 之间的函数关系式.(3)知识拓展6.现从A ，B 向甲、乙两地运送蔬菜，A ，B 两个蔬菜市场各有蔬菜14吨，其中甲地需要蔬菜15吨，乙地需要蔬菜13吨，从A 到甲地运费50元/吨，到乙地30元/吨；从B 地到甲运费60元/吨，到乙地45元/吨．（1）设A 地到甲地运送蔬菜x 吨，请完成下表：运往甲地(单位：吨) 运往乙地(单位：吨) P A B C13.58A xB（2）设总运费为W元，请写出W与x的函数关系式．（3）怎样调运蔬菜才能使运费最少？答案:1. C.2. 23b =. 3. 126s t =-，（012t ≤≤）；一次函数. 4. 1902y x =+，(0180)x <<；y 是x 的一次函数. 5. 61.5cm ；13.5 1.5(1)12 1.5y x x x =--=+.6.（1）（2）由题意，得5030146015451W x x x x =+-+-+-（）（）（）整理得，51275W x =+．（3）∵A ，B 到两地运送的蔬菜为非负数，∴0,140,150,10.x x x x ≥⎧⎪-≥⎪⎨-≥⎪⎪-≥⎩ 解不等式组，得114x ≤≤ 在51275W x =+中，W 随x 增大而增大， ∴当x 最小为1时，W 有最小值 1280元．运往甲地(单位：吨) 运往乙地(单位：吨) A x 14x - B 15x - 1x -。

小学二年级语文分层作业设计一、设计目的为提高小学二年级学生在语文学习过程中的兴趣，挖掘学生潜能，促进个性化发展，实现教学目标，特制定本分层作业设计。

二、作业分层标准1. 基础层：掌握课文生字、词语、句子，能够正确、流利地朗读课文。

2. 提高层：在基础层的基础上，理解课文内容，能够用自己的话复述课文，运用所学知识进行简单的写作。

3. 拓展层：在前两层的基础上，深入分析课文，理解作者意图，能够进行创意写作和课外阅读。

三、作业内容设计1. 基础层：（1）生字词学习：每个课时学习5-10个生字词，通过听写、组词、造句等形式巩固。

（2）课文朗读：每天安排一篇课文，要求学生正确、流利地朗读，家长签字确认。

2. 提高层：（1）课文理解：针对每个课时，设计1-2道理解性问题，要求学生用自己的话回答。

（2）写作练习：每周一篇小练笔，结合所学课文，进行仿写、续写等。

3. 拓展层：（1）课文分析：每周选取一篇课文，进行深入分析，理解作者写作手法和意图。

（2）创意写作：每月一次，结合所学知识，进行创意写作。

（3）课外阅读：每学期推荐一本课外读物，要求学生完成阅读笔记。

四、作业评价与反馈1. 作业评价：教师对每个学生的作业进行评价，分为优秀、良好、合格、不合格四个等级。

2. 反馈机制：针对学生作业中存在的问题，教师及时给予指导和建议，帮助学生提高。

3. 定期总结：每学期末，对学生的作业完成情况进行总结，为下学期的教学提供参考。

五、作业布置与批改1. 布置原则：结合教学进度和分层标准，合理布置作业。

2. 批改要求：教师认真批改学生作业，及时给予评价和反馈。

3. 家长参与：鼓励家长参与学生作业的完成过程，关注学生学习情况。

六、作业完成时间1. 基础层：每天30分钟内完成。

2. 提高层：每周1小时内完成。

3. 拓展层：根据实际情况，每周1-2小时内完成。

七、注意事项1. 教师应关注学生个体差异，合理调整作业难度。

2. 学生应养成良好的学习习惯，按时完成作业。