第三章行波法(2)

第3章 波动问题的行波法§3.1 二阶线性方程的分类与化简本节讨论：①两个自变量方程的分类与化简，②多个自变量方程的分类与化简⒈ 两个自变量方程的分类与化简二阶方程的一般形式 二阶变系数方程可写为1112220(,)2(,,,,)(,)xx xy yy x y Lu x y a u a u a u x y u u u f x y =+++Φ= (3.1.1)式中：11a 、12a 、22a 为x 、y 的函数，0(,,,,)x y x y u u u Φ为低阶导数项。

公式关于二阶导数项为线性的，即称方程为准线性的。

若0(,,,,)x y x y u u u Φ关于u 及其x u 、y u 为线性的，则称方程为线性的。

方程的变换 为了简化上述方程，作可逆变换：(,)(,)x y x y ξξηη=⎧⎨=⎩， (,)0(,)J x y ξη∂=≠∂， (,)(,)x x y y ξηξη=⎧⎨=⎩(3.1.2) 代入方程中，不难得到：11122212(,,,,)(,)Lu A u A u A u u u u f ξξξηηηξηξηξη=+++Φ= (3.1.3)式中： 22111112222x x y yA a a a ξξξξ=++ (3.1.4) 12111222()x x x y y x y y A a a a ξηξηξηξη=+++ (3.1.5)22221112222x x y yA a a a ηηηη=++ (3.1.6) 我们化简的目的是使得二次项的项数尽量少，并且值尽量为简单（如0ij A =或1ij A =±）。

顾及ij A 的表达式，取关于z 的一阶非线性偏微分方程2211122220x x y y a z a z z a z ++= (3.1.7)若该方程有解),(1y x z ϕ=、),(2y x z ψ=，则110A =及220A =；公式大大简化了。

第三章行波法与积分变换法在第二章中，讨论了分离变量法，它是求解有限区域内定解问题的一个常用方法，只要求解的区域很规则（其边界在某种坐标系中的方程能用若干个只含有一个坐标变量的方程表示），对三种典型的方程均可运用。

本章介绍另外两个求解定解问题的方法，一是行波法，一是积分变化法。

行波法只能用于求解无界域内波动方程的定解问题，积分变换法不受方程类型的限制，主要用于无界域，但对有界域也能应用。

§3.1 一维波动方程的达朗贝尔（D’Alembert）要求一个常微分方程的特解，惯用的方法是先求出它的通解，然后利用初始条件确定通解中的任意常数得到特解。

对于偏微分方程能否采用类似的方法呢？一般来说是不行的，原因之一是在偏微分方程中很难定义通解的概念，原因之二是即使对某些方程能够定义并求出它的通解，但此通解中包含有任意函数，要由定解条件确定出这些任意函数是会遇到很大困难的。

但事情不是绝对得，在少数情况下不仅可以求出偏微分方程的通解（指包含有任意函数的解），而且可以由通解求出特解。

本节就一维波动方程来建立它的通解公式，然后由它得到初值问题解的表达式。

对于一维波动方程22222u u a t x ∂∂=∂∂ （3.1） 作如下代换：x at x at ξη=+⎧⎨=-⎩（3.2） 利用复合函数微分法则，得u u u u u x x x ξηξηξη∂∂∂∂∂∂∂=+=+∂∂∂∂∂∂∂ 2222222()()2u u u u u x x xu u u ξηξξηηξηξξηη∂∂∂∂∂∂∂∂∂=+++∂∂∂∂∂∂∂∂∂∂∂∂=++∂∂∂∂ （3.3）同理有2222222222()()[2]u u u u u a a t u u u a ξξηηξηξξηη∂∂∂∂∂∂∂=---∂∂∂∂∂∂∂∂∂∂=-+∂∂∂∂ （3.4）将（3.3）及（3.4）代入（3.1）得20u ξη∂=∂∂ （3.5） 将（3.5）式对η积分得()u f ξξ∂=∂，（()f ξ是ξ的任意可微函数） 在对此式对ξ积分得212(,)()()()()u x t f d f f x at f x at ξξη=+=++-⎰ （3.6）其中1f ，2f 都是任意二次连续可微函数。

第三章行波法数理方法研究物理和工程问题的三大步骤：1、写出定解问题2、求解3、分析解答我们已经学会了导出方程和写出定解条件（定解问题）的基本方法，下边的重点是求解和解答过程：各种求解数学物理方程的方法，主要包括：1、行波法2、分离变量法3、积分变换法4、格林函数法5、保角变换法本章问题的引入：1、无限长细弦的抖动（一维）2、投石入水中形成的圆形扩散波（二维）3、灯塔上的灯光（三维）若当研究问题时只关心一端时间某处发生的振动，边界的影响还来不及达到该处，波将一直向前传播，称此为行进波（行波），解决这类行波问题引入了行波法。

中心：用行波法求解无界空间波动问题。

1、掌握达朗贝尔公式的应用和行波法解题步骤；2、有源问题化为无源问题的冲量法；3、三维问题化为一维问题的平均值法。

三、分析解答：1、适定性的证明：（1）解存在：并且满足泛定方程和定解条件；利用公式（2）唯一性：因为f 1和f 2的任意性已经由定解条件确定，所以解是唯一的。

（3）稳定性：不妨设：()()()()110022|, |t t t x x u u x x ϕψϕψ==⎧⎧⎪⎪==⎨⎨⎪⎪⎩⎩()()()()1212||,||x x x x ϕϕδψψδ−≤−≤2、行波法：（1）它基于波动的特点；（2）引入了坐标变换简化方程；（3）优点：求解方式易于理解，求解波动方程十分方便；（4）缺点：通解不易求，有局限性。

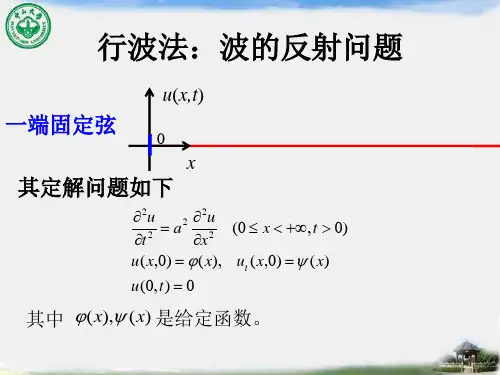
习题 3.12232110, (,0)0, (,0)1;(3) 0, (,0), (,0);8230(,0)3(,0)0tt xx t tt xx t xx xy yy yu a u u x u x u a u u x x u x x u u u u x x u x −===−===+−=⎧⎪=⎨⎪=⎩、确定下列初值问题的解：（）、解下列初值(仅需思考，选作）问题：OXYZ(,,)M x y z 0000(,,)M x y z ϕθ处的解和xyzz ′x ′y ′ϕθ(,,)M x y z ′′′′(,,)M x y z泊松公式的物理意义：定解问题在M 点t 时刻的值与以M 点为中心，以at 为半径的球面上的初值确定的。

第三章 行波法§3.1 达朗贝尔法（行波法）考虑无界弦的自由振动问题，有定解问题如下：⎪⎪⎪⎩⎪⎪⎪⎨⎧==∂∂=∂∂)()0,()()0,(22222x x u x x u x u a t u tψϕ ∞+<∞-+∞<<∞->+∞<<∞-x x t x 0, 对于上面的标准形方程，它有两族特征曲线1c at x =+，2c at x =-作变换at x +=ξ，at x -=η由上面的方程变为：02=∂∂∂ηξu 求上面偏微分方程的解先对η积分一次得)(1ξηf u =∂∂ 再对ξ积分一次得：⎰+=+=)()()()(2ηξηξξG F f d f u其中G F ,是具有任意连续可微函数，将原自变量代回得原方程的通解为)()(),(at x G at x F t x u -++=下面通过初始条件确定上面的任意函数G F ,∵ )(0x u t ϕ==，)(0x u t t ψ==∴ )()()(x x G x F ϕ=+ （1）)()()(//x x aG x aF ψ=- （2）对（2）从0x 到x 积分得：⎰-+=-x x x G x F d ax G x F 0)()()(1)()(00ααψ （3）（1）+（3）得)]()([21)(21)(21)(000x G x F d a x x F x x -++=⎰ααψϕ ⎰---=x x x G x F d a x x G 0)]()([21)(21)(21)(00ααψϕ ∴ ⎰+-+++-=at x atx d a at x at x t x u ααψϕϕ)(21)]()([21),( 该公式叫达朗贝尔公式例：确定初值问题：⎪⎩⎪⎨⎧==>∞+<∞∂∂=∂∂-122222)0,( cos )0,(0 e x u x x u ,t x -x u a t u t 解：略。

达朗贝尔方程的物理定义：先讨论0)(=x ψ （即振动只有初始位移）)]()([21),(at x at x t x u ++-=ϕϕ 先看)(at x -ϕ项：当0=t 时若观察者位于c x =处，此时 )()(c at x ϕϕ=-在x 轴上，若观察者以速度a 沿轴正方向运动，则在t 时刻观察者位于at c x +=处，此时：)()()(c at at c at x ϕϕϕ=-+=-由于t 是任意的，这说明观察者在运动过程中随时可以看到相同的波形，可见，波形和观察者一样，以速度a 沿x 轴正方向传播。