乘法公式(1)

高等数学一(微积分)常用公式表-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN1、乘法公式（1）（a+b ）²=a 2+2ab+b 2 （2）(a-b)²=a ²-2ab+b ²（3）(a+b)(a-b)=a ²-b ² （4）a ³+b ³=(a+b)(a ²-ab+b ²) （5）a ³-b ³=(a-b)(a ²+ab+b ²)2、指数公式：（1）a 0=1 （a ≠0）（2）a P -=P a 1（a ≠0）（3）amn=mna（4）a m a n =a n m +（5）a m ÷a n=n m aa =a nm -（6）（am）n =amn（7）（ab ）n =a n b n（8）（b a）n =n n ba （9）（a ）2=a （10）2a =|a|3、指数与对数关系： （1）若a b=N ，则N b a log = （2）若10b=N ，则b=lgN （3）若be =N ，则b=㏑N4、对数公式： （1）b a b a =log , ㏑eb=b （2）N aaN=log ，eNln =N（3）aN N a ln ln log =（4）a b be aln = （5）N M MN ln ln ln +=（6）N M NMln ln ln -= （7）Mn M n ln ln =（8）㏑nM =M nln 15、三角恒等式：（1）（Sin α）²+（Cos α）²=1 （2）1+（tan α）²=(sec α)²（3）1+(cot α)²=(csc α)²（4）αααtan cos sin =（5）αααcot sin cos =（6）ααtan 1cot =（7）ααcos 1csc =（8）ααcos 1sec =7.倍角公式： （1）αααcos sin 22sin = （2）ααα2tan 1tan 22tan -=（3）ααααα2222sin 211cos 2sin cos 2cos -=-=-=8.半角公式（降幂公式）：（1）（2sin α）2=2cos 1a - （2）（2cosα）2=2cos 1a + （3）2tan α=a a sin cos 1+=a acos 1sin +常用公式表（二）1、求导法则：（1）（u+v ）/=u /+v / （2）（u-v ）/=u /-v /（3）（cu ）/=cu / （4）（uv ）/=uv /+u/v （5）2v v u v u v u '-'='⎪⎭⎫ ⎝⎛ 5、定积分公式：（1）⎰⎰=babadtt f dx x f )()( （2）⎰=aadx x f 0)(（3）()()dx x f dx x f abba⎰⎰-= （4）⎰⎰⎰+=bac ab cdxx f dx x f dx x f )()()(（5）若f （x ）是[-a,a]的连续奇函数，则⎰-=aadx x f 0)(（6）若f （x ）是[-a,a]的连续偶函数，则6、积分定理：（1）()()x f dt t f xa ='⎥⎦⎤⎢⎣⎡⎰ ()()()()()[]()()[]()x a x a f x b x b f dt t f x b x a '-'='⎥⎦⎤⎢⎣⎡⎰2（3）若F （x ）是f （x ）的一个原函数，则)()()()(a F b F x F dx x f ba b a -==⎰7.积分表()C x x xdx ++=⎰tan sec ln sec 1 ()C x x xdx +-=⎰cot csc ln csc 2()C a xa dx x a +=+⎰arctan 11322 ()C a x dx x a +=-⎰arcsin 1422()C a x ax a dx ax ++-=-⎰ln 211522 8．积分方法()()bax x f +=1；设：t b ax =+()()222x a x f -=；设：t a x sin = ()22a x x f -=；设：t a x sec =()22x a x f +=；设：t a x tan =()3分部积分法：⎰⎰-=vdu uv udv。

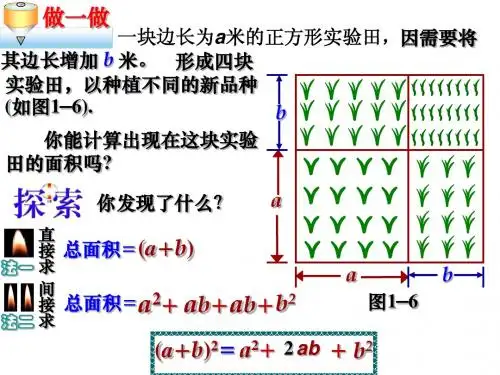
乘法公式和因式分解（一）、知识点：1、单项式乘单项式：单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

2、单项式乘多项式：单项式与多项式相乘，用单项式乘多项式的的每一项，再把所得的积相加。

m(a+b－c)＝ma+mb－mc3、多项式乘多项式：多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。

(a+b)(c+d)=ac+ad+bc+bd(二)、知识要点 1、乘法公式2、因式分解因式分解：（1）把一个多项式写成几个整式的积的形式叫做多项式的因式分解。

注、公因式：各项都含有的公共的因式叫做这个多项式各项的公因式。

（2）多项式的乘法与多项式因式分解的区别简单地说：乘法是积化和，因式分解是和化积。

3、因式分解的方法： （1）、提公因式法：如果多项式的各项有公因式，可以把这个公因式提到括号外面，将多项式写成因式乘积的形式，这种分解因式的方法叫做提公因式法。

（2）、运用公式法：运用乘法公式把一个多项式因式分解的方法叫运用公式法。

（3）、分组分解法：把各项适当分组，先使分解因式能分组进行，再使分解因式在各组之间进行． （4）、十字相乘法：有些二次三项式，可以把第一项和第三项的系数分别分解为两个数之积，然后借助画十字交叉线的方法，把二次三项式进行因式分解，这种方法叫十字相乘法。

简单的说十字相乘法就是：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数。

注意：十字相乘法不是适合所有二次三项式，只有在一次项系数和二次项系数以及常数项存在一种特殊关系时才能用，这个特殊关系我们通过例题来说明： 注意：我们在用十字相乘法之前一定要根据第一步判断是否能用十字相乘法。

我们在分解常数项和二次项系数时变化多端，目的是交叉相乘之和要等于一次项系数，如何分配常数项和二次项系数要根据情况而定。

很有用的乘法速算公式-CAL-FENGHAI.-(YICAI)-Company One11.十几乘十几：口诀：头乘头，尾加尾，尾乘尾。

例：12×14=解: 1×1=1２＋４＝６２×４＝８12×14=168注：个位相乘，不够两位数要用0占位。

２.头相同，尾互补(尾相加等于10)：口诀：一个头加１后，头乘头，尾乘尾。

例：23×27=解：２＋１＝３２×３＝６３×７＝2123×27=621注：个位相乘，不够两位数要用0占位。

３.第一个乘数互补，另一个乘数数字相同：口诀：一个头加１后，头乘头，尾乘尾。

例：37×44=解：3+1=44×4=167×4=2837×44=1628注：个位相乘，不够两位数要用0占位。

４.几十一乘几十一：口诀：头乘头，头加头，尾乘尾。

例：21×41=解：2×4=82+4=61×1=121×41=861５.11乘任意数：口诀：首尾不动下落，中间之和下拉。

例：11×23125=解：2+3=53+1=41+2=32+5=72和5分别在首尾11×23125=254375注：和满十要进一。

６.十几乘任意数：口诀：第二乘数首位不动向下落，第一因数的个位乘以第二因数后面每一个数字，加下一位数，再向下落。

例：13×326=解：13个位是33×3+2=113×2+6=123×6=1813×326=4238注：和满十要进一。

指数函数运算公式8个
指数函数是形如y=a^x的函数，其中a是底数，x是幂。

指数函数具有以下8个运算公式：
1.乘法公式：
a^x*a^y=a^(x+y)
这个公式说明了相同底数的指数函数相乘时，底数不变，指数相加。

2.除法公式：
(a^x)/(a^y)=a^(x-y)
这个公式说明了相同底数的指数函数相除时，底数不变，指数相减。

3.平方公式：
(a^x)^y=a^(x*y)
这个公式说明了指数函数的指数也可以是指数。

4.根式公式：
(a^x)^(1/y)=a^(x/y)
这个公式说明了指数函数可以求根号。

5.幂公式：
(a^x)^y=a^(x*y)
这个公式说明了对一个指数函数求幂时，可以将指数间的乘法提到指数外面。

6.对数公式：
loga (a^x) = x
这个公式说明了对一个指数函数求底数为a的对数时，可以得到其指数。

7.指数和对数互补公式：
a^loga (x) = x
这个公式说明了对一个以底数为x的对数函数求以底数为a的指数时，结果是x。

8.复合函数公式：
g(f(x))=(a^x)^y
=a^(x*y)
这个公式说明了一个指数函数作为复合函数时，可以把两个指数相乘。

这些指数函数运算公式是指数函数的基本性质，通过这些公式可以对
指数函数进行各种运算和简化。

对于求解指数函数的实际问题，这些公式
具有重要的应用价值。

乘法的所有公式乘法是数学中最基本的算术运算之一，用于计算两个数的积。

下面列出了乘法的所有公式，供大家参考：1. 乘法的基本性质乘法具有以下基本性质：- 交换律：a × b = b × a- 结合律：(a × b) × c = a × (b × c)- 分配律：a × (b + c) = (a × b) + (a × c)2. 乘法的特殊形式乘法有一些特殊形式，其中包括：- 任何数乘以1等于它本身：a × 1 = a- 任何数乘以0等于0：a × 0 = 0- 任何数乘以-1等于它的相反数：a × -1 = -a- 任何负数的积是正数，任何正数的积是正数，一个正数和一个负数的积是负数3. 乘法的幂乘法的幂是指一个数自乘若干次的运算，用上标表示。

比如，2³表示2自乘3次，即2×2×2=8。

乘法的幂有以下公式：- a的负n次方等于1/(a的正n次方)：a^-n = 1/a^n- a的0次方等于1：a^0 = 1- a的正n次方等于a自乘n次：a^n = a × a × ... × a (共n个a)4. 乘法的简便计算在乘法的计算中，有一些简便计算方法：- 乘法竖式：将两个数竖着排列，从个位开始相乘，得到的结果逐位相加。

- 合并同类项：将两个数相乘后，将同类项合并，即将相同的字母因数相乘，并将指数相加。

- 借位乘法：在小学的乘法计算中，如果有一个位上的乘积大于9，就需要借位，这种方法被称为借位乘法。

5. 乘法的应用乘法在数学中广泛应用于不同的领域中，比如：- 代数学中，乘法是多项式运算中的重要运算。

- 几何学中，乘法用于计算面积、体积等。

- 物理学中，乘法用于计算力、功等。

- 经济学中，乘法用于计算利润、成本等。

总的来说，乘法是一项十分基本的数学运算，能够在各个领域中发挥重要作用。

乘法公式知识讲解乘法公式是指在数学中用于求解乘法运算的规则。

它们是数学中最基本也是最重要的公式之一，常用于求解各种复杂的乘法运算，可以大大简化计算过程。

在这篇文章中，我将详细介绍乘法公式的相关知识，并为大家提供一些实例来帮助理解。

首先，我们来讨论最基本的乘法公式，即两个数的乘法。

设有两个数a和b，它们的乘积可以表示为a × b或ab。

在乘法中，我们通常使用乘号（×）或圆点（·）来表示乘法运算。

下面是一些常见的乘法公式：1.乘法交换律：a×b=b×a乘法交换律表示，两个数相乘的结果与两个数的顺序无关。

例如，3×4=4×3=122.乘法结合律：(a×b)×c=a×(b×c)乘法结合律表示，三个数相乘的结果与它们的运算顺序无关。

例如，(2×3)×4=2×(3×4)=243.数值相同的乘法：a×a=a^2数值相同的乘法表示，一个数与其自身相乘的结果可以用该数的平方来表示。

例如，4×4=4^2=16接下来，我们将进一步讨论乘法公式的应用。

1.乘法分配律：a×(b+c)=(a×b)+(a×c)乘法分配律是乘法中的一个重要规则。

它表示一个数乘以两个数的和等于该数分别乘以这两个数后的和。

例如，2×(3+4)=(2×3)+(2×4)=142.幂与乘法：a^m×a^n=a^(m+n)幂与乘法表示，两个具有相同底数的幂相乘，底数不变，指数相加。

例如，2^3×2^4=2^(3+4)=2^7=1283.倒数乘法：a×(1/a)=1倒数乘法表示一个数与其倒数相乘的结果等于1、例如，5×(1/5)=14.零乘法：a×0=0零乘法表示任何数与0相乘的结果都是0。

乘法运算公式
乘法运算是学习数学的基础，也是日常工作、学习中必不可少的基本运算。

乘法运算公式是由奥地利数学家费尔期发现，他发现乘法公式可以由加减乘除中的任意两个组合出来，就是我们现在熟悉的公式：a×b=b+b+b+…（a次）。

按照这个公式，可以得出a × b（a≥0，b≥1）的结果。

首先将b累加a次，因此乘法运算是将乘数（这里的b）乘以被乘数（这里的a）的次数，得出的结果就是两个数的乘积。

举个例子，8×5=5+5+5+5+5+5+5+5=40，得出乘法运算的结果就是40。

让乘法运算变得更简单的一个方法是九九乘法表，它把乘法运算的公式进行简单的排列组合，使得学习者更容易理解乘法运算的原理和计算方式。

乘法运算几乎在日常生活和学习中都会使用，比如烹饪、建筑等，它们都会用到乘法运算来精确控制和计算。

另外，学习者也可以运用乘法运算理解更高难度的数学概念，比如组合数、概率等。

由此可见，乘法运算在我们的日常生活中起着至关重要的作用，只有掌握了乘法运算的基础知识，才能更好地掌握数学，并进一步深入学习。

乘法的三种运算定律公式乘法是初等数学中的基础运算之一，它可以用于两个或多个数的相乘。

在乘法运算中，有着许多基本的性质和规则，其中最重要的三个运算定律公式为结合律、交换律和分配律。

1. 结合律：结合律是指在三个或更多项的乘法运算中，不改变因子的顺序可以改变乘积的分组方式。

表述为(a×b)×c = a×(b×c)。

例如，对于2×3×4，可以将先将2和3相乘得到6，再将6和4相乘得到24，也可以先将3和4相乘得到12，再将2和12相乘得到24。

这就是结合律的表现。

乘法结合律的证明方法有很多种，其中一种方法是使用数学归纳法。

首先，任意三个自然数 a、b 和 c，可以通过结合律得到下列式子：(a×b)×c = a×(b×c)然后，当我们增加一个新因子 d 时，我们可以应用结合律来重新组合它们，得到：((a×b)×c)×d = (a×b)×(c×d) =a×(b×(c×d)) = a×((b×c)×d)因此，在数学归纳法的证明中，我们可以认为结合律适用于有限数量的任意自然数上。

2. 交换律：交换律是指在两项乘积中，可以改变它们的次序而保持其值不变。

表述为a×b = b×a。

例如，2×3=3×2。

这表明在乘法中，因子可以任意交换而不改变乘积的值。

交换律的证明相对简单，可以用数学归纳法证明。

首先，在两个自然数 a 和 b 上，如果应用交换律，我们可以得到：a×b = b×a然后，假设交换律在所有 k 个自然数上都成立。

当增加一个因子 c 时，我们可以将它插入到乘积公式中并交换其顺序得到：(a×b)×c = (b×a)×c = b×(a×c) = c×(b×a) = c×a×b因此，交换律对任意数量的自然数同样适用。

1.十几乘十几：口诀：头乘头，尾加尾，尾乘尾。

例：12×14=？解: 1×1=1２＋４＝６２×４＝８12×14=168注：个位相乘，不够两位数要用0占位。

２.头相同，尾互补(尾相加等于10)：口诀：一个头加１后，头乘头，尾乘尾。

例：23×27=？解：２＋１＝３２×３＝６３×７＝2123×27=621注：个位相乘，不够两位数要用0占位。

３.第一个乘数互补，另一个乘数数字相同：口诀：一个头加１后，头乘头，尾乘尾。

例：37×44=？解：3+1=44×4=167×4=2837×44=1628注：个位相乘，不够两位数要用0占位。

４.几十一乘几十一：口诀：头乘头，头加头，尾乘尾。

例：21×41=？解：2×4=82+4=61×1=121×41=861５.11乘任意数：口诀：首尾不动下落，中间之和下拉。

例：11×23125=？解：2+3=53+1=41+2=32+5=72和5分别在首尾11×23125=254375注：和满十要进一。

６.十几乘任意数：口诀：第二乘数首位不动向下落，第一因数的个位乘以第二因数后面每一个数字，加下一位数，再向下落。

例：13×326=？解：13个位是33×3+2=113×2+6=123×6=1813×326=4238注：和满十要进一。

初中数学什么是乘法公式乘法公式是指数学中用于求解乘法运算的一些基本公式。

这些公式可以帮助我们简化乘法运算，从而更快速地计算结果。

在初中数学中，有几个常见的乘法公式，包括分配律、同底数幂相乘法则、平方差公式和立方差公式等。

下面我将详细解释这些乘法公式，并给出示例来说明如何应用它们。

1. 分配律：分配律是乘法公式中的基本法则之一。

它表示两个数分别与一个数的和（或差）相乘，等于这两个数分别与这个数相乘后再相加（或相减）。

具体的表达式如下：a × (b + c) = a × b + a × ca × (b - c) = a × b - a × c示例：计算3 × (4 + 2)：3 × (4 + 2) = 3 × 4 + 3 × 2 = 12 + 6 = 18计算5 × (7 - 3)：5 × (7 - 3) = 5 × 7 - 5 × 3 = 35 - 15 = 202. 同底数幂相乘法则：同底数幂相乘法则适用于两个具有相同底数的幂相乘的情况。

在这种情况下，我们只需要将底数保持不变，指数相加即可。

具体的表达式如下：a^m × a^n = a^(m + n)示例：计算2^3 × 2^4：2^3 × 2^4 = 2^(3 + 4) = 2^7 = 1283. 平方差公式：平方差公式用于将一个算式表示为两个数的平方差的形式。

具体的表达式如下：a^2 - b^2 = (a + b)(a - b)示例：将9^2 - 4^2 表示为两个数的平方差的形式：9^2 - 4^2 = (9 + 4)(9 - 4) = 13 × 5 = 654. 立方差公式：立方差公式用于将一个算式表示为两个数的立方差的形式。

具体的表达式如下：a^3 - b^3 = (a - b)(a^2 + ab + b^2)示例：将8^3 - 2^3 表示为两个数的立方差的形式：8^3 - 2^3 = (8 - 2)(8^2 + 8 × 2 + 2^2) = 6 × 68 = 408这些乘法公式在数学中非常常见，并且可以帮助我们简化乘法运算。

二年级数学公式大全表必背二年级学生在学习数学的时候，需要掌握一些基本的数学公式，这些公式可以帮助他们更好地理解数学知识，提高计算能力。

下面是二年级数学公式大全表，并按照列表划分好，希望对学生们的数学学习有所帮助。

一、加法公式1、加法交换律：a+b=b+a2、加法结合律：(a+b)+c=a+(b+c)3、零元素：a+0=0+a=a4、加法逆元：a+(-a)=0二、减法公式1、减法定义：a-b=a+(-b)2、减法同加法：a-b=-（b-a）三、乘法公式1、乘法交换律：a×b=b×a2、乘法结合律：(a×b)×c=a×(b×c)3、乘法分配律：a×(b+c)=a×b+a×c4、乘法单位元素：a×1=1×a=a5、乘法零元素：a×0=0×a=0四、除法公式1、除法定义：a÷b=a×1/b2、除法分配律：(a+b)÷c=(a÷c)+(b÷c)五、算术平均数公式1、算术平均数定义：a1+a2+…+an=n×平均数六、面积公式1、正方形面积：S=a×a (a为正方形的边长)2、矩形面积：S=a×b (a、b为矩形的长和宽)3、三角形面积：S=1/2×底×高 (底为底边长度，高为垂直于底边的线段长度)4、梯形面积：S=(上底+下底)×高/2 (上底和下底为梯形的边长，高为梯形的高度)七、周长公式1、正方形周长：C=4×a (a为正方形的边长)2、矩形周长：C=2×(a+b) (a、b为矩形的长和宽)3、三角形周长：C=a+b+c (a、b、c为三角形的三条边长)4、圆周长：C=2×π×r (π≈3.14，r为圆的半径)以上就是二年级数学公式大全表，学生们可以根据这些公式来进行数学计算，提高数学能力，取得更好的成绩。

乘法公式（1）一 选择题1.下列可以用平方差公式计算的是( )A 、(x －y) (x + y)B 、(x －y) (y －x)C 、(x －y)(－y + x)D 、(x －y)(－x + y)2.下列各式中，运算结果是22169b a -的是( )A 、)43)(43(b a b a --+-B 、)34)(34(a b a b --+-C 、)34)(34(a b a b -+D 、)83)(23(b a b a -+3.下列各式中,计算结果为x 2-16y 2的是( )A.()()y x y x 82-+B.()()y x y x 16-+C.()()x y x y ++-44D.()()y x y x 44+-- 4.22)213()213(-+a a 等于( )A 、4192-a B 、161814-a C 、161298124+-a a D 、161298124++a a 5.在下列多项式的乘法中，可以用平方差公式计算的是（ ）A 、(x+3)(x-3)B 、(a+0.5b)(0.5b-a)C 、(-x+y)(x-y)D 、(a 2-b)(a+b 2)6.（-m+2n ）2的运算结果是( )A 、m 2+4mn+4n 2 B 、-m 2-4mn+4n 2 C 、m 2-4mn+4n 2 D 、m 2-2mn+4n 27.运算结果为1-2x 2+4x 4的是( )A 、22)1(x +- B 、22)1(x + C 、22)1(x -- D 、2)1(x - 8若x 2+2mx+[ ]是完全平方式，则[ ]应填入的代数式（ ）A.m B.-m C.m 2 D.±m9.如果m-n=1／5, m 2+n 2=51／25,那么(mn)2005的值为( )A.1 B.-1 C.0 D.无法确定10.若4x 2-Mxy+9y 2是两数和的平方,则M 的值是( ) A.36 B.±36 C.12 D.±12 二 填空题1.下列多项式①（m －n ）（n －m ）②（a+b ）（－a －b ）③（－a －b ）（a －b ）④（a+b ）（a+b ），可以用平方差公式计算的是______2.已知（a+b ）2=7，（a-b ）2=4则a 2+b 2=______，ab=______3.要使x 2-6x+k 是完全平方式，则k=________4.要使y 2+my+4成为完全平方式，那么m=________5.将多项式x 2+9加上一个整式，使它成为完全平方式，这个整式可以是_______________6.计算（a －b ）（a+b ）（a 2+b 2）（a 4－b 4）的结果是_______________7.若9m 2-25n 2=20，且3m+5n=4，则3m-5n=8.若x 2+kx+0.25=（x －0.5）2，则k=_______；若x 2－kx+1是完全平方式，则k=______9.填写算式： ① (－7m －11n) (11n －7m) = __________________；②（2y-x ）（-x-2y ）=_______________；③（a-2）（a 2+4）（a+2）=_________________；④(-3ab 2+2a 2b)(3ab 2+2a 2b)=_______________10.填写算式：① (－7m －8n) 2 = __________________；②（3y-4x ）2=_______________；③〔（-3a-2）（2-3a ）〕2=_________________； 三 解答题1.计算 ①（-5m+4）2 ②（-2x-3）2 ③(ab+5)(ab-5) ④(-x-3y)(-x+3y) ⑤（1－3y ）（1+3y ）（1+9y 2）⑥（x －2）（x+2）－（x+1）（x －3） ⑦（ab+1）2－（ab －1）2 ⑧（1-x ）（1+x ）（1+x 2）（1+x 4）2.运用乘法公式简便计算 ①9982 ②197×2033.先化简，再求值 ①2(3x 1)(x 2)(x 2)4x(x 2)-+-+--，其中x=－1②[（xy+2）（xy －2）－3x 2y 2+4]，其中x=10，y=－1254.若x+y=6，xy=3，求2()x y -，22x y xy +的值5.已知(x-y)2=4,(x+y)2=64，，求下列代数式的值：（1）x 2+y 2；（2）xy6.若a=2005，b=2006，c=2007，求a 2+b 2+c 2-ab-bc-ac 的值7.观察下列算式：111122⨯=-，222233⨯=-，333344⨯=-，…… ,（1）猜想并写出第n 个等式；（2）证明你写出的等式的正确性8.如图，边长为a 的正方形内有一个边长为b 的小正方形，①请用a 、b 的代数式表示图1中阴影部分的面积；②小明把阴影部分拼成了一个长方形，如图2，这个长方形的长和宽分别是多少？③比较① ②的结果，你能验证平方差公式吗？。