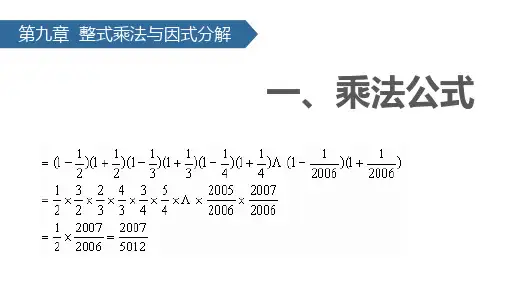
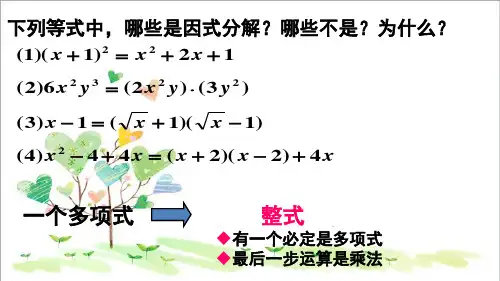
乘法公式课件ppt
- 格式:ppt
- 大小:526.00 KB
- 文档页数:23









消防控制室值班制度及消防控制室管理及应急程序一、消防控制室值班制度消防控制室是保障单位消防安全的重要部门,为了确保消防控制室的正常运行和及时响应各类应急情况,制定一套科学合理的值班制度是非常必要的。
1. 值班人员的职责和要求值班人员是消防控制室的核心力量,他们需要具备以下职责和要求:(1)24小时轮班,确保消防控制室的连续运行。
(2)熟悉消防设备的操作和维护,能够及时处理各类消防报警。
(3)掌握应急预案和操作流程,能够迅速响应各类紧急情况。
(4)具备较强的沟通和协调能力,能够与其他部门和外部单位进行有效的信息交流。
(5)保持良好的工作状态和精神状态,确保能够高效地应对各类突发情况。
2. 值班制度的安排(1)根据消防控制室的工作量和人员数量,制定合理的值班班次和轮班制度。
(2)确保每个班次都有足够的人员配备,避免因人员不足而导致值班工作的疏漏。
(3)制定值班人员的换班规定,确保换班时的交接工作顺利进行,避免信息的遗漏和传递不及时。
(4)定期进行值班人员的培训和考核,提高他们的专业素质和应急处理能力。
二、消防控制室的管理消防控制室是一个高度机密的地方,管理工作的严谨性和规范性对于消防安全至关重要。
1. 人员管理(1)建立健全的人员管理制度,包括招聘、培训、考核和奖惩等方面的规定。
(2)对消防控制室的工作人员进行背景调查和安全审查,确保其具备良好的品行和职业操守。
(3)定期对消防控制室的工作人员进行岗位培训和技能培训,提高他们的专业水平和应急处理能力。
(4)建立健全的考核制度,对工作人员的工作情况进行定期评估,发现问题及时进行纠正和改进。
2. 设备管理(1)建立健全的设备管理制度,确保消防设备的正常运行和有效维护。
(2)定期对消防设备进行检查和维护,及时发现和解决设备故障,确保其处于良好的工作状态。
(3)建立设备档案,记录设备的购置、维修和更换等信息,方便日后的管理和维护工作。
(4)加强对设备的保密工作,确保设备信息不被泄露,防止设备被非法操作和损坏。