9.4乘法公式(1)

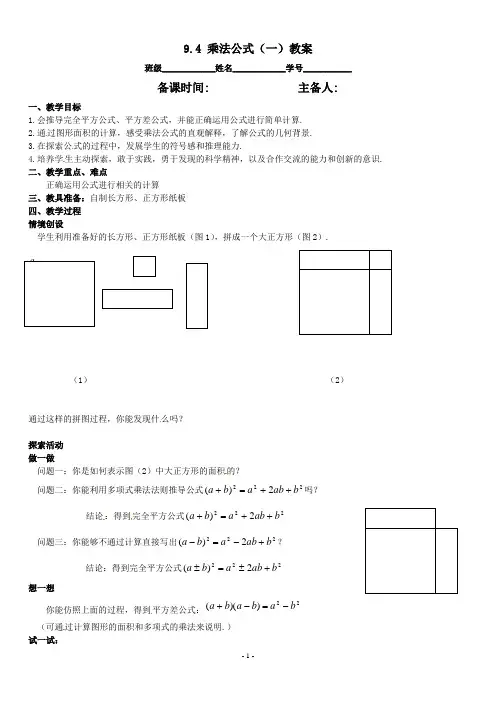
9.4 乘法公式（一）教案班级____________姓名____________学号___________备课时间: 主备人:一、教学目标1.会推导完全平方公式、平方差公式，并能正确运用公式进行简单计算.2.通过图形面积的计算，感受乘法公式的直观解释，了解公式的几何背景.3.在探索公式的过程中，发展学生的符号感和推理能力.4.培养学生主动探索，敢于实践，勇于发现的科学精神，以及合作交流的能力和创新的意识.二、教学重点、难点正确运用公式进行相关的计算三、教具准备：自制长方形、正方形纸板四、教学过程情境创设学生利用准备好的长方形、正方形纸板（图1），拼成一个大正方形（图2）.（1）（2）通过这样的拼图过程，你能发现什么吗？探索活动做一做问题一：你是如何表示图（2）中大正方形的面积的？问题二：你能利用多项式乘法法则推导公式2222)(b ab a b a ++=+吗？结论：得到完全平方公式2222)(b ab a b a ++=+问题三：你能够不通过计算直接写出2222)(b ab a b a +-=-？结论：得到完全平方公式2222)(b ab a b a +±=±想一想你能仿照上面的过程，得到平方差公式：22))((b a b a b a -=-+ （可通过计算图形的面积和多项式的乘法来说明.）试一试：1.计算（1）2)2(+x （2）2)2(-x （3）)2)(2(-+x x（4）2)52(+a （5）2)52(--a练一练（1）))()((22y x y x y x ++- （2）1)12)(12)(12)(12(842+++++3.计算（1）21.10 （2）2999练一练（1）98102⨯ （2）19952005⨯小结（1） 分别说出完全平方公式、平方差公式的特征（2） 在式子bd ad bc ac d c b a +++=++))((中当a 、b 、c 、d 满足什么关系时，由它可得到乘法公式？ 作业：P80练一练1、2、3、4。

自主学习任务单-------9.4 乘法公式一、学习目标1．会推导完全平方公式，并能运用公式进行简单的计算；2．通过图形面积的计算，感受乘法公式的直观解释；3．经历探索完全平方公式的过程，发展学生的符号感和推理能力．二、学习过程（一）活动：做一做1.你能用代数式表示图中大正方形的面积吗？你可以用几种方法表示？2. 你能用多项式的乘法法则计算()2+吗？请你写出来.a b3. 例1 计算()2-.a b（二）新知：请你尝试用文字语言来叙述这两个等式.()2222a b a ab b +=++ ()2222a b a ab b -=-+（三）例题用完全平方公式计算(1) ()253p + ； (2) ()227x y - ；(3) ()22x y -+ ； (4) ()225a -- .拓展：用完全平方公式计算(1)2199 ； (2) ()2a b c ++.三、效果检测1. 下面的计算是否正确？如有错误，请改正.(1)222()x y x y -＝－˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙（ ）(2)222(2)a b a ab b ---＝+ ˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙（ ）(3)22224()2m n m n mn +++＝ ˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙˙（ ） (4)22422111124a b a b a b ⎛⎫-=-+ ⎪⎝⎭ ˙˙˙˙˙˙˙˙˙˙˙˙˙˙（ ） 2．填空：如果229x kxy y ++是一个完全平方公式展开后的结果，那么常数k 的值为 .3. 填空：一个正方形的边长为(6)acm a >.若边长减少6cm ， 则这个正方形的面积减少了 2cm .4. 用完全平方公式计算：(1) ()223x y + ； (2) 2142a ⎛⎫-+ ⎪⎝⎭ ；(3) 2302 ； (4) ()2a b c -+ .5.已知2x y +=，1xy =，求()2x y +和22x y +的值.6.已知7a b -=，2ab =，求22a b +和()2a b +的值.附件1：教材内容附件2: 检测答案1. (1) 错误，原式222x xy y =-+.(2) 错误，原式()2=a b +222a ab b =++.(3) 错误，原式()22=222m m n n +⋅⋅+2244m mn n =++.(4) 正确，原式222224211=21121142a b a b a b a b ⎛⎫-⨯⋅+=- ⎪⎭+⎝. 2．6±解析：()222223699x y x xy y x kxy y ±=±+=++Q ，6k ∴=±. 3. 1236a -解析：正方形的面积减少了()()2222612361236a a a a a a --=--+=- 4. (1) 原式()()2222233x x y y =+⋅⋅+224129x xy y =++(2) 原式221124422a a ⎛⎫⎛⎫=-+⋅-⋅+ ⎪ ⎪⎝⎭⎝⎭214164a a =-+ (3)原式()222300230023002291204=+=+⨯⨯+=(4) 原式()2a b c =-+⎡⎤⎣⎦()()222a b a b c c =-+-+222222a ab b ac bc c =-++-+ 222222a b c ab ac bc =++-+-5. 解：将2x y +=两边平方得，()24x y +=， 即2224x y xy ++=，把1xy =代入得：222x y +=.6. 解：将7a b -=两边平方得：()222249a b a b ab -=+-=， 把2ab =代入得：22449a b +-=，即2253a b +=，则()222253457a b a b ab +=++=+=.。

9.4乘法公式（完全平方公式）班级 姓名 学号 等第 教学目标：(1) 探索并推导完全平方公式、并能运用公式进行简单的计算； (2) 引导学生感受转化的数学思想以及知识间的内在联系。

教学重点：完全平方公式；教学难点：正确的应用完全平方公式、进行计算教学方法：探索、引导法教具准备：三角尺、投影仪 a 教学过程：一. 情景创设 b如右图：你能通过不同的方法计算大正方形的面积吗？ 从而你发现了什么？ 二. 探索活动问题一：如何用字母表示上图中大正方形的面积？ 生： 将上图看成一个大正方形，则面积为 2)(b a +。

师：很好，还有没有其它的方法呢？生：可将上图看成是由两个小长方形和两个小正方形组成的图形，那么它的面积为222b ab a ++。

师：两种方法都求出了大正方形的面积，从而我们可以发现什么呢？ 生：2)(b a +=222b ab a ++ 这个公式就叫做一个完全平方公式。

问题二：你能用多项式的乘法法则推导公式2)(b a +=222b ab a ++吗？ 生：2)(b a +=))((b a b a ++=22b ba ab a +++=222b ab a ++ 师：很好，你能用同样的方法计算2)(b a -吗？生：222222))(()(b ab a b ba ab a b a b a b a +-=---=--=- 即：2222)(b ab a b a +-=-，这是我们要学习的另一个完全平方公式。

完全平方公式：2)(b a + 222b ab a ++=2222)(b ab a b a +-=-师：你能用文字语言叙述这两个公式吗？两数和 (差)的平方等于这两数的平方和加上 （减去）这两数乘积的两倍师：你能说出这两个公式的特点吗？生：左边是：两数和 （差）的平方. 右边是: 两数的平方和加上（减去）这两数乘积的两倍. 三. 范例点睛例1 计算：( a – b )2想一想：你有几种方法计算 (a -b )2例2 用完全平方公式计算(1) ( 5 + 3p )2 (2) ( 2x - 7y )2例3 用完全平方公式计算（1）（ -x + 2y ）2 (2) ( -2a - 5)2例4 用完全平方公式计算 （1）9982 （2） 1012例4：填空题：（注意分析，找出a 、b ）①()()2216=++x ； ②()()()22243=+-y x③()()22=+-ab a ；④()()225025=++ab a ⑤()-+=⎪⎭⎫ ⎝⎛-2224116214y x y x⑥()()222b ab a b a ++=+- ()()222b ab a b a +-=-+例5．已知3=+y x ，2=xy ，求①22y x +；②yx 11+四．随堂练习1、用完全平方公式计算 (1)（1＋x ）2 （2） (y -4)2（3） ( x − 2y )2 （4） (2x y + x )22. 一个正方形的边长为a c m 。

苏科版数学七年级下册《9.4 乘法公式》说课稿3一. 教材分析乘法公式是数学中的一种基本公式，广泛应用于各个领域。

苏科版数学七年级下册《9.4 乘法公式》这一节主要介绍了平方差公式和完全平方公式。

平方差公式可以帮助我们简化计算，快速求出两个数的平方差；而完全平方公式则可以帮助我们求出一个数的平方，或者两个数的乘积的平方。

这两个公式在解决实际问题中具有重要的作用。

二. 学情分析学生在学习这一节之前，已经学习了有理数的乘法、乘方等基础知识，对于公式有一定的认识。

但乘法公式较为抽象，需要学生在理解的基础上进行记忆。

同时，学生需要掌握如何将实际问题转化为乘法公式的形式，从而解决问题。

三. 说教学目标1.知识与技能目标：学生能够掌握平方差公式和完全平方公式，并能够灵活运用这两个公式解决实际问题。

2.过程与方法目标：通过小组合作、讨论等方式，培养学生主动探究、合作学习的意识，提高学生的数学思维能力。

3.情感态度与价值观目标：培养学生对数学的兴趣，增强学生自信心，使学生能够积极主动地参与到数学学习中。

四. 说教学重难点1.重点：平方差公式和完全平方公式的记忆与运用。

2.难点：如何将实际问题转化为乘法公式的形式，以及如何在复杂问题中灵活运用乘法公式。

五. 说教学方法与手段1.采用启发式教学，引导学生主动探究、发现规律，培养学生的数学思维能力。

2.利用多媒体课件，生动形象地展示乘法公式的推导过程，帮助学生理解记忆。

3.小组合作、讨论，鼓励学生发表自己的观点，培养学生的合作意识。

4.创设实际问题情境，引导学生运用乘法公式解决问题，提高学生的应用能力。

六. 说教学过程1.导入：通过复习有理数的乘法、乘方等基础知识，引出本节课的主题——乘法公式。

2.讲解：讲解平方差公式和完全平方公式的推导过程，让学生理解并记忆这两个公式。

3.练习：布置一些简单的练习题，让学生运用平方差公式和完全平方公式进行计算，巩固所学知识。

4.应用：创设一些实际问题情境，让学生运用乘法公式解决问题，培养学生的应用能力。

《平方差公式》教学案一、教材分析“平方差公式”是苏教版七年级数学（下册）第九章《从面积到乘法公式》的教学内容，是学习了整式的乘法运算后为了简化计算而归纳的一个公式，是对多项式乘法中出现的较为特殊的算式归纳、总结；是从一般到特殊的认识过程的范例，也是进一步学习完全平方公式、进行相关代数运算与变形的重要知识基础。

它的依据是多项式乘以多项式法则以及合并同类项法则。

“平方差公式”这一内容属于数学再创造活动的结果，教材为学生在数学活动中获得数学思想方法、提高能力提供了良好的契机，它在整式乘法、因式分解、分式运算及其它代数式的变形中起着十分重要的作用，因此，是构建学生有价值的数学知识体系并形成相应数学技能的重要内容，是让学生感悟换元思想，感受数学再创造的好教材。

二、教学目标知识目标：会推导平方差公式，了解公式的几何背景，并能运用公式进行计算。

能力目标：通过平方差公式的运用，培养学生运用公式的能力、分析、综合和概括能力。

情感目标：培养学生从特殊到一般、从一般到特殊的思维能力，让学生在合作探究的学习过程中体验成功的喜悦，培养学生善于观察、大胆创新的思维品质。

三、教学重点掌握公式的结构特征，并学会正确运用公式。

四、教学难点理解平方差公式的结构特征，灵活运用平方差公式。

五、教学问题诊断分析1.学生刚学过多项式乘法，已经具备学习和运用平方差公式的知识结构。

2.多项式相乘的形式复杂多变，学生较容易被假象所迷惑；学生学习能力也参差不齐，部分学生对多项式相乘还不够熟练和细心。

3.学生的基础能力存在差异，在猜想过程中分不同层次，请学生大胆地猜测出公式，并对公式有一个直观的认识。

4.为突破难点，可采用小组合作、先体验后归纳的教学方式，使学生从中感悟换元和数形结合的数学思想。

5.大部分学生都能通过探索小结出平方差公式的特点，但在具体的问题中，还是有些同学会“判断失误”，关键在于要抓住平方差公式的本质。

在完成练习后，应该及时小结平方差公式应用的前提。