下载文档原格式
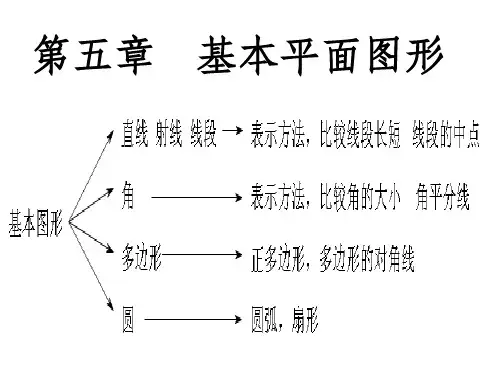
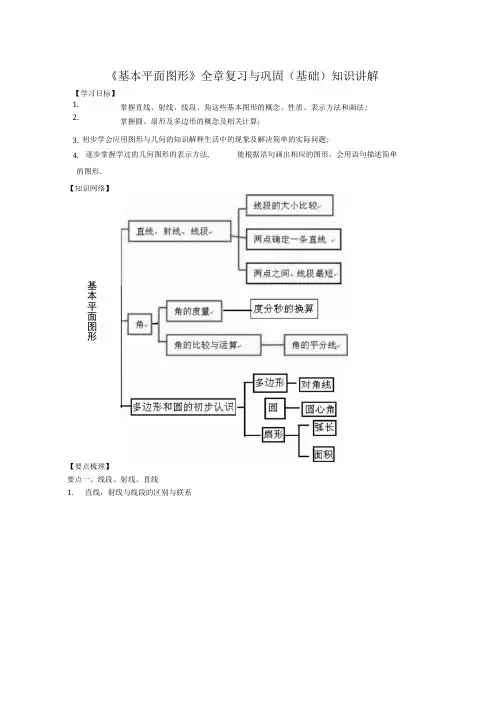
《基本平面图形》全章复习与巩固（基础）知识讲解掌握直线、射线、线段、角这些基本图形的概念、性质、表示方法和画法; 掌握圆、扇形及多边形的概念及相关计算；初步学会应用图形与几何的知识解释生活中的现象及解决简单的实际问题;的图形. 【知识网络】【要点梳理】要点一、线段、射线、直线1.直线，射线与线段的区别与联系【学习目标】1. 2.4. 逐步掌握学过的几何图形的表示方法,能根据语句画出相应的图形，会用语句描述简单3. 基本平面图形类别、直线射线图形表示方法A B '①两个大写字母；②一个小写字母A B '①角个大写字母(表示蠕点的字母在U);②一个小写字母A B1①表示两端点的两个大写字母;②一个小写字母端点个数无1个2个延伸性的两方无限延伸向一方无限延伸不可延伸性成两点确定一条JL线两点之间，成段最短SB不可以不可以可以作图叙述过作直以4为端点作射我,48连接m2.基本性质(1)直线的性质:两点确定一条直线.(2)线段的性质:两点之间，线段最短.要点诠释：①本知识点可用来解释很多生活中的现象.如：要在墙上固定一个木条，只要两个钉子就可以了，因为如果把木条看作一条直线，那么两点可确定一条直线.②连接两点间的线段的长度，叫做两点的距离.3.画一条线段等于已知线段(1)度量法：可用直尺先量出线段的长度，再画一条等于这个长度的线段.(2)用尺规作图法：用圆规在射线AC上截取AB=a,如下图：4.线段的比较与运算(1)线段的比较：比较两条线段的长短,(2)线段的和与差:如下图，有AB+BC=AC,或AC=a+b； AD=AB-BD。
A aB b CA D B(3)线段的中点：把一条线段分成两条相等线段的点，叫做线段的中点.如下图，有：AM=MB = -AB2要点诠释:常用两种方法，一种是度量法；一种是叠合法.①线段中点的等价表述：如上图，点M在线段AB上，且有AM=-AB,则点M为线段2AB的中点.②除线段的中点（即二等分点）夕卜，类似的还有线段的三等分点、四等分点等.如下图，点M, N.P 均为线段AB的四等分点.0 --------------- ® ----------------- 9---------------------0 ------------------ •A M N P BAM = MN = NP=PB = -AB4要点二、角1.角的度量（1）角的定义：有公共端点的两条射线组成的图形叫做角，这个公共端点是角的顶点，这两条射线是角的两条边；此外，角也可以看作由一条射线绕着它的端点旋转而形成的图形.（2）角的表示方法：角通常有三种表示方法：一是用三个大写英文字母表示，二是用角的顶点的一个大写英文字母表示，三是用一个小写希腊字母或一个数字表示.例如下图：要点诠释：①角的两种定义是从不同角度对角进行的定义；②当一个角的顶点有多个角的时候，不能用顶点的一个大写字母来表示.（3）角度制及角度的换算1周角=360° , 1平角=180° , 1° =60' , 1' =60”,以度、分、秒为单位的角的度量制，叫做角度制.要点诠释：①度、分、秒的换算是60进制，与时间中的小时分钟秒的换算相同.②度分秒之间的转化方法：由度化为度分秒的形式（即从高级单位向低级单位转化）时用乘法逐级进行；由度分秒的形式化成度（即低级单位向高级单位转化）时用除法逐级进行.③同种形式相加减：度加（减）度，分加（减）分，秒加（减）秒；超60进一，减一成60.（4）角的分类：(5)画一个角等于已知角(1)借助三角尺能画出15°的倍数的角，在0〜180°之间共能画出11个角.(2)借助量角器能画出给定度数的角.(3)用尺规作图法.2.角的比较与运算(1)角的比较方法：①度量法；②叠合法.(2)角的平分线：从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线，例如:如下图，因为0C是ZA0B的平分线，所以Z1=Z2=- ZA0B,或ZAOB=2Z1=2Z2.2类似地，还有角的三等分线等.3.方位角以正北、正南方向为基准，描述物体运动的方向，这种表示方向的角叫做方位角.要点诠释：(1)方位角还可以看成是将正北或正南的射线旋转一定角度而形成的.所以在应用中一要确定其始边是正北还是正南.二要确定其旋转方向是向东还是向西，三要确定旋转角度的大小.(2)北偏东45°通常叫做东北方向，北偏西45°通常叫做西北方向，南偏东45°通常叫做东南方向，南偏西45°通常叫做西南方向.(3)方位角在航行、测绘等实际生活中的应用十分广泛.要点三、多边形和圆的初步认识1.多边形及正多边形:多边形是由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形.其中，各边相等、各角也相等的多边形叫做正多边形.如下图：五边形正六边形要点诠释：(1)n边形有n个顶点、n条边，对角线的条数为虹主.2(2)多边形按边数的不同可分为三角形、四边形、五边形、六边形等.2.圆及扇形：(1)圆：如图，在一个平面内，线段0A绕它固定的一个端点。
平面图形的认识复习课（教案）20232024学年数学六年级下册人教版教学内容：本节课主要复习平面图形的基本概念和性质，包括点、线、面的基本概念，直线、射线、线段的特点和区别，角的概念和分类，以及平行线和垂线的性质。
通过复习，使学生能够熟练掌握平面图形的基本概念和性质，提高解题能力。
教学目标：1. 知识与技能：使学生能够熟练掌握平面图形的基本概念和性质，包括点、线、面的基本概念，直线、射线、线段的特点和区别，角的概念和分类，以及平行线和垂线的性质。
2. 过程与方法：通过引导学生自主探究和合作交流，培养他们的观察能力、分析能力和逻辑思维能力。
3. 情感态度价值观：激发学生对数学的兴趣和好奇心，培养他们积极主动的学习态度和合作精神。
教学难点：1. 直线、射线、线段的特点和区别。
2. 角的概念和分类。
3. 平行线和垂线的性质。
教具学具准备：1. 教具：直线、射线、线段模型，角度模型，平行线和垂线模型。
2. 学具：学生自备直尺、量角器、圆规等绘图工具。
教学过程：一、导入1. 引导学生回顾平面图形的基本概念和性质，包括点、线、面的基本概念，直线、射线、线段的特点和区别，角的概念和分类，以及平行线和垂线的性质。
2. 提问：同学们，我们之前学习了平面图形的基本概念和性质，那么谁能告诉我直线、射线、线段有什么区别呢？角的概念和分类又是怎样的呢？平行线和垂线又有哪些性质呢？二、新课导入1. 讲解直线、射线、线段的特点和区别，通过模型展示和举例说明，使学生理解并掌握。
2. 讲解角的概念和分类，通过模型展示和举例说明，使学生理解并掌握。
3. 讲解平行线和垂线的性质，通过模型展示和举例说明，使学生理解并掌握。
三、巩固练习1. 发放练习题，让学生独立完成，巩固所学知识。
2. 讲解练习题，解答学生的疑问，确保学生理解并掌握。
2. 提问：同学们，通过本节课的学习，我们复习了平面图形的基本概念和性质，那么谁能告诉我直线、射线、线段的特点和区别？角的概念和分类又是怎样的呢？平行线和垂线又有哪些性质呢？板书设计：平面图形的认识复习课一、直线、射线、线段的特点和区别二、角的概念和分类三、平行线和垂线的性质作业设计：1. 完成练习题，巩固所学知识。
第五章 基本平面图形 复习课
一、基础知识回顾：
1、在墙上钉一根水平方向的木条，至少需要 个钉子，用数学知识解释为
2、如图，图中线段和射线的条数分别为 。
3、已知线段AB ，请用尺规按下列要求组图：
（1）延长AB 到C ，使BC=AB ；（2）延长BA 到D ，使AD=AC 。
若AB=2cm ，那么AC= cm ，BD cm ，CD cm 。
4、如图，C 、D 是数轴上两点，它们分别表示有理数-2.4，1.6，O 为原点，则线段CD 的中点A 表示的有理数是 。
5、在∠AOB 的的内部，从顶点O 引出三条射线OC 、OD 、OE ，图中共有 个角，若引5条射线呢？若引n 条射线呢？
6、1.45º= '= ''，1800''= '= º。
7、如图，OC 是∠AOB 的平分线，∠DOB = 13
∠COD ， ∠DOB=15º，那么∠COD = ，∠BOC = ，∠AOB =
8、若扇形甲的面积占圆的面积的15%，则此扇形的圆心角
为 ，十边形从一个顶点可引出 条对角线，可分成
三角形，一共可画出 条对角线。
二、知识网络构建
三、变式深化
1、如果点C 在AB 上,下列表达式①AC=12
AB;②AB=2BC;③AC=BC;④AC+BC=AB 中, 能表示C 是AB 中点的有( ) A.1个 B.2个 C.3个 D.4个
2、如图所示，从A 地到达B 地，最短的路线是（ ）．
A ．A →C →E →
B B ．A →F →E →B
C ．A →
D →
E →B D ．A →C →G →E →B
3、如下图,∠AOC=∠BOD=90°。
（1）若 ∠BOC=38° ,求∠AOD 的度数. （2）图中相等的角有哪些？（3）若∠BOC 变小，∠AOD 如何变化？（4）利用三角板在图中画一个与∠AOB 相等的角。
4、从n 边形的一个顶点出发，可以画 条对角线，n 边形总共有 条对角线。
5、将一个半径为10cm 的圆分成3个扇形，其圆心角的比1：2：3，求：
①各个扇形的圆心角的度数。
②其中最小一个扇形的面积。
6、如图所示,OE 平分∠BOC,OD 平分∠AOC,∠COE=20.6°, ∠COD=40°40′,•求∠AOB 的度数.
四、经典探究
O C A D B E C B A D O
1、如图，AB>CD ，则AC 与BD 的大小关系是 。
2、已知A 、B 、C 三点在同一条直线上，M 、N 分别为线段AB 、BC 的中点，且AB=60，BC=40，则MN 的长为 。
3、如图，∠AOB=90°，∠AOC 是锐角，OF 平分∠AOC ，OE 平分∠BOC ，求∠EOF 的度数。
4、已知线段a 和b ，求作线段MN ，使MN=a+b 。
五、应用拓展
1、同一平面内互不重合的三条直线的交点的个数是（ ）.
A 、可能是0个，1个，2个
B 、可能是0个，2个，3个
C 、可能是0个，1个，2个或3个
D 、可能是1个，3个
2、下列说法中，正确的有（ ）.
①过两点有且只有一条直线；②连接两点的线段叫做两点的距离；③两点之间，线段最短；④若AB=BC ，则点B 是线段AC 的中点．A 、1 B 、2个 C 、3个 D 、4个
3、钟表上12时15分钟时，时针与分针的夹角为（ ）.
A 、90°
B 、82.5°
C 、67.5°
D 、60°
4、按下列线段长度，可以确定点A 、B 、C 不在同一条直线上的是（ ）.
A 、AB=8cm ，BC=19cm ，AC=27cm
B 、AB=10cm ，BC=9cm ，AC=18cm
C 、AB=11cm ，BC=21cm ，AC=10cm
D 、AB=30cm ，BC=12cm ，AC=18cm
5、已知OA ⊥OC ，过点O 作射线OB,且∠AOB=30°，则∠BOC 的度数为（ ）.
A 、30°
B 、150°
C 、30°或150°
D 、以上都不对
6、点A ，B ，P 在同一直线上，下列说法正确的是（ ）．
(A)若AB =2PA ，则P 是AB 的中点 (B)若AP =PB ，则P 是AB 的中点
(C)若AB =2PB ，则P 是AB 的中点 (D)若AB =2PA =2PB ，则P 是AB 的中点
7、如图，点C 是线段AB 上一点，点M 是AC 的中点，点N 是BC 的中点，如果MC 比NC 长2cm ，AC 比BC 长（ ）．
(A)1 cm (B)2 cm (C)4 cm (D)6 cm 8、平面内的6条直线两两相交，最多有（ ）个交点．(A)12 (B)15 (C)16 (D)20
9、一个钝角的平分线和这个角的一边形成的角一定是（ ）．
(A)锐角 (B)钝角 (C)直角 (D)平角
10、如图，圆的四条半径分别是OA ，OB ，OC ，OD ，其中点O ，A ，B
在同一条直线上，∠AOB ＝90°，∠AOC ＝3∠BOC ，那么圆被四条半径分成的四个扇形的面积的比是（ ）
(A)1∶2∶2∶3 (B) 3∶2∶2∶3 (C) 4∶2∶2∶3 (D) 1∶2∶2∶1
11、0.15°= ′= ″. 12、若∠1：∠2：∠3=1：2：3，且∠1+∠2+∠3=180°， 则∠2= 度.
13、钟表在3点30分时，时针与分针所成的锐角是 度.
A B
C M N O A B C D
A
E
B D
C 14、直线AB 上有一点C ，直线AB 外有一点P ，由A 、B 、C 、P 四点可以确定 条线段。
15、从五边形的一个顶点出发可以画出 条对
角线；过多边形的一个顶点的所有对角线，将这个多
边形分成8个三角形，这个多边形是 边形。
16、把一副三角尺如图所示拼在一起， 试确定图中∠A 、∠B 、∠AEB 、∠ACD 的度数，
并用“＜”将它们连起来。
17、如图所示, 点O 是直线AB 上一点.
∠AOC=30°,∠BOD=60°.
（1）求∠COD 的度数.
（2）若OM 、ON 分别是∠AOC、∠BOD 的角平分线,
求∠MON 的度数.
18、如图，OE 为∠AOD 的平分线，
∠COD=41∠EOC ，∠COD=15°. 求：①∠EOC 的大小； ②∠AOD 的大小.
19、在直线l 上有两点A 、B ，已知A 、B 两点之间的距离为6cm ，点C 在直线l 上，回答下面的问题：
（1）是否存在点C ，使点C 与点A 、B 之间的距离之和等于5cm ，为什么？
（2）是否存在点C ，使点C 与点A 、B 之间的距离之和等于6cm ，点C 的位置应该在哪里？这样的点C 有多少个？ C D E
O l。
