第3—4章复习思考和作业题(有附加题,含答案)

七年级下册数学三四章期末复习题学习目的：1、会用迷信记数法表示数. 用近似数表示生活中的数量，了解有效数字是什么，会从统计图中尽能够多地获取信息，能笼统、有效地运用统计图描画数据;2、了解肯定事情、不能够事情和不确定事情发作的能够性大小，了解事情发作的等能够性及游戏规那么的公允性、会求事情发作的概率。

了解概率的计算方法。

能设计契合要求的复杂概率模型。

一、主要内容：1、迷信记数法。

如：用迷信记数法表示：(1)、0.0000045= ，(2)、-0.006= ，(3)、30200= ，(4)、-5200= ，(5)、-0.000203=2、3、(1)人的头发丝直径大约是710-3米，那么一根头发丝直径是百万分之一米的倍.(2)近似数0.03601有个有效数字，区分是 ;近似数2.4万有个有效数字，它准确到位;2.40万有个有效数字，准确到位;近似数3.6104有个有效数字，它准确到位;4、能够性的大小、概率(1)普通地，就事情发作的能够性而言，可将事情分为、和。

(2)小明在一个小正方体的六个面上区分标了1、2、3、4、5、6六个数字，随意地掷出小正方体，那么P(掷出地数字小于7)=________. P(掷出地数字等于7)=________.(3)王刚设计了一个转盘游戏：随意转动转盘，使指针最后落在白色区域的概率为1/3，假设他将转盘等分红12份，那么白色区域应占的份数是 .(4)游戏的公允性是指双方获胜的概率5、将以下事情发作的概率标在以下图中.(1)50年后地球将消逝;(2)投一枚硬币正面朝上;(3)10个苹果分装三个果盘里,一定有一个果盘里至少装4个苹果.6、如图，线段AB的长度准确到10厘米是___厘米，有___个有效数字.7、课本P106 5、P112转盘、P126 例18、小狗在如下图的方砖上走来走去，最终停在黑砖上的概率为( )A. B. C. D .二、课堂训练1、以下各题的数，是准确数的是( )A.初一有800名同窗B.月球距离地球38万千米C.小明身高148cm D.明天气温估量28℃2、将2.4697准确到千分位是( ) A、2.469B、2.460 C、2.47D、2.4703、6.510-3用小数可表示为( ) A.0.0065 B.0.00065 C.0.065D. 0.0000654、以下事情发作的概率为0的是( )A.小明买体彩中了大奖B.小强的体重25公斤C.某年有370天 D .未来三天有强降雨5、小明用一枚平均的硬币实验，前7次掷得的结果都是反面向上，假设将第8次掷得反面向上的概率记为P，那么( )A、P=0.5B、P0.5C、P0.5D、无法确定6、一幅扑克去掉大小王后，从中任抽一张是红桃的概率是( ) A. B. C. D.7、关于四舍五入失掉的近似数3.20215，以下说法正确的选项是( )A.有3个有效数字，准确到百分位B.有6个有效数字，准确到个位C.有2个有效数字，准确到万位D.有3个有效数字，准确到千位8、一箱苹果的质量是10.90千克,这箱苹果可近似的看作是10千克，这是准确到了( )A.10千克B. 1千克C.0.1千克D. 0.01千克9、一个袋子中装有5个白球，3个红球，甲摸到白球，乙摸到红球胜，为使甲、乙两人获胜的能够性一样大，那么必需往袋中再放入个球.10、甲、乙两同窗做掷骰子游戏,骰子是平均的正方体,六个面区分刻有1、2、3、4、5、6六个数.游戏规则:掷一次2的倍数朝上,甲同窗获胜;掷一次朝上的数字大于3那么乙同窗获胜.你以为这个游戏公允吗?请说明理由.新课标第一网三、晚间练习1.以下数据中，准确的是( )A、第五次人口普查说明，我国人口总数为12.9533亿人B、某词典共有1234页C、珠穆朗玛峰的高度为海拔8848米D、小明的身高为167厘米2. 以下说法正确的选项是( )A、四舍五入失掉的近似数49.0是准确到个位，有效数字是4、9两个B、四舍五入失掉的近似数21.00是准确到百分位，有效数字是2、1、0、0四个C、两个近似数1千和1000的准确度是相反的D、近似数2.30和2.3是一样的3、一个口袋中有8个红球,2个黑球,每个球除颜色不同外,其他都相反,假定从中恣意拿出3个球,那么以下结论成立的是()A.所取3个球中至少有1个是黑球B.所取3个球中至少有2个是红球C.所取3个球中至少有1个是红球D.所取3个球中最多有2个红球4、小明所在的七年级二班有54人,在投票选举班长时,小明得了28票,超越半数且票数第一,中选班长,那么小明当班长的支持率为() A. B. C. D.5、1纳米= 米，某种植物花粉的直径约为35000纳米，那么用迷信记数法表示该种花粉的直径为( ) A 3.5 米 B 3.5 米C 3.5 米D 3.5 米6、一箱灯泡有24个，合格率为80%，从中恣意拿一个是次品的概率为( )A、 B、80% C、 D、17、柜子里有5双鞋，取出右脚穿的鞋的概率为( )A、1/10B、1/5C、1/3D、1/28、李明用6个球设计了一个摸球游戏，共有四种方案，一定不能成功的是( )A. 摸到黄球、红球、白球的概率区分为、、B. 摸到黄球、红球的概率是C. 摸到黄球的概率是，摸到红球、白球的概率都是D.摸到黄球、红球、白球的概率都是9、某种原子的半径为0.00000000021米，用迷信记数法可表示为 ;近似数0.05010有个有效数字，准确到位;近似数5.3万有个有效数字，它准确到位; 近似数9.06104有个有效数字，它准确到位;256700保管两位有效数字，写成 ; 10、用10个球设计一个摸球游戏，(1)使摸到红球的概率为 ;(2)使摸到红球和白球的概率都是 (各球除颜色不同外其他均相反).11、设计了一个转盘游戏：随意转动转盘，使指针最后落在白色区域的概率为。

学案4章末总结一、光的折射定律、全反射规律的应用几何光学是以光线为工具研究光的传播规律，所以解决几何光学问题的关键是根据“光的传播规律”画出光路图，然后再利用几何学知识，寻找相应的边角关系．(1)几何光学主要包括四条原理：①光的直线传播规律；②光的反射定律；③光的折射定律；④光路可逆原理．其中折射定律、不同色光的折射率、全反射现象是高考的重点和热点．解题时常用的三个公式：①折射定律公式：n＝sin isin r；②折射率与速度的关系：n＝cv；③全反射的临界角：sin C＝1n.(2)注意法线的画法：法线画成虚线；法线垂直于界面，如果界面是圆面，那应该垂直于圆的切线，即法线沿半径指向圆心．例1(2012·山东·37(2))如图1所示，一玻璃球体的半径为R，O为球心，AB为直径．来自B点的光线BM在M点射出，出射光线平行于AB，另一光线BN恰好在N点发生全反射．已知∠ABM＝30°，求：图1①玻璃的折射率；②球心O到BN的距离．解析 ①设光线BM 在M 点的入射角为i ，折射角为r ，由几何知识可知i ＝30°，r ＝60°，根据折射定律得n ＝sin rsin i代入数据得n ＝ 3②光线BN 恰好在N 点发生全反射，则∠BNO 为临界角C ，sin C ＝1n设球心到BN 的距离为d ，由几何知识可知：d ＝R sin C联立解得d ＝33R .答案 ①3 ②33R例2 如图2所示，某种透明物质制成的直角三棱镜ABC ，∠A 等于30°.一束光线在纸面内垂直AB 面射入棱镜，如图2所示，发现光线刚好不能从BC 面射出，而是最后从AC 面射出．求：图2(1)透明物质的折射率n .(2)光线从AC 面射出时的折射角α.(结果可以用α的三角函数表示)解析 (1)由题意可知，光线从AB 面垂直射入，恰好在BC 面发生全反射，光线最后从AC 面射出，光路图如图所示．设该透明物质的临界角为C ，由几何关系可知C ＝θ1＝θ2＝60°，sin C ＝1n解得：n ＝233(2)由几何关系知：β＝30°由折射定律知n ＝sin αsin β解得：sin α＝33，α＝arcsin 33 答案 (1)233 (2)arcsin 33二、测折射率的方法测折射率常见的方法有成像法、插针法及全反射法，不管哪种方法其实质相同，由折射定律知n ＝sin θ1sin θ2，只要确定出入射角θ1及折射角θ2即可测出介质的折射率，下面以测定水的折射率为例对上述方法举例说明． (1)成像法原理：利用水面的反射成像和水的折射成像．图3方法举例：如图3所示，在一盛满水的烧杯中，紧挨杯口竖直插一直尺，在直尺的对面观察水面，能同时看到直尺在水中的部分和露出水面部分的像，若从P 点看到直尺在水下最低点的刻度B 的像B ′(折射成像)恰好跟直尺在水面上刻度A 的像A ′(反射成像)重合，读出AC 、BC 的长，量出烧杯内径d ，即可求出水的折射率 n ＝(BC 2＋d 2)/(AC 2＋d 2). (2)插针法原理：光的折射定律．图4方法举例：如图4所示，取一方木板，在板上画出互相垂直的两条线AB 、MN ，从它们的交点O 处画直线OP (使∠PON <45°)，在直线OP 上的P 、Q 两点垂直插两枚大头针．把木板放入水中，使AB 与水面相平，MN 与水面垂直．在水面上观察，调整视线使P 的像被Q 的像挡住，再在木板S 、T 处各插一枚大头针，使S 挡住Q 、P 的像，T 挡住S 及Q 、P 的像．从水中取出木板，画出直线ST ，量出图中的角θ1、θ2，则水的折射率n ＝sin θ1/sin θ2. (3)全反射法 原理：全反射现象．图5方法举例：在一盛满水的大玻璃缸下面放一发光电珠，如图5所示．在水面上观察，看到一圆的发光面，量出发光面直径D 及水深h ，则水的折射率n ＝D 2＋4h 2D .例3 某同学利用“插针法”测定玻璃的折射率，所用的玻璃砖两面平行．正确操作后，作出的光路图及测出的相关角度如图6所示．(1)此玻璃的折射率计算式为n ＝________(用图中的θ1、θ2表示)；(2)如果有几块宽度大小不同的平行玻璃砖可供选择，为了减小误差，应选用宽度________(填“大”或“小”)的玻璃砖来测量．图6解析 据题意可知入射角为(90°－θ1)，折射角为(90°－θ2)，则玻璃的折射率为n ＝sin (90°－θ1)sin (90°－θ2)＝cos θ1cos θ2；玻璃砖越宽，光线在玻璃砖内的传播方向越容易确定，测量结果越准确．故应选用宽度大的玻璃砖来测量．答案 (1)cos θ1cos θ2⎣⎢⎡⎦⎥⎤或sin (90°－θ1)sin (90°－θ2) (2)大 三、光的波速、折射率与频率的综合应用例4 半圆形玻璃砖横截面如图7所示，AB 为直径，O 点为圆心．在该界面内有a 、b 两束单色可见光从空气垂直于AB 射入玻璃砖，两入射点到O 点的距离相等．两束光在半圆边界上反射和折射的情况如图4所示，则a 、b 两束光( )图7A ．在同种均匀介质中传播，a 光的传播速度大B ．以相同的入射角从空气斜射入水中，b 光的折射角大C ．从同一介质以相同的入射角射向空气，若a 光不能进入空气，则b 光也不能进入空气D ．a 光的频率大于b 光的频率解析由于两束光的入射点到O点的距离相等，因此它们在半圆边界上的入射角相同，由于b光发生全反射，而a光能够折射，说明b光的全反射临界角小于a光的全反射临界角，由n＝1sin C可知，b光在介质中的折射率大于a光在介质中的折射率，所以b光的频率比a光的频率高，由v＝cn可知，在同种介质中a光的传播速度大，A项正确，D项错误；以相同的入射角从空气斜射入水中，b光的折射程度大，折射角小，B项错误；由于b光全反射临界角小，所以C项正确．答案AC1．(光的折射定律)一束复色光由空气射向一块平行平面玻璃砖，经折射分成两束单色光a、b.已知a光的频率小于b光的频率．下列光路图中可能正确的是()答案 B解析由于a光的频率小于b光的频率，a光在玻璃中的折射率小于b光在玻璃中的折射率，由两种单色光进入玻璃后偏折程度不同且玻璃砖两平面平行，可判定B正确．2．(光的折射定律)如图8所示，一束复色光从空气中沿半圆形玻璃砖半径方向射入，从玻璃砖射出后分成a、b两束单色光．则()图8A．玻璃砖对a光的折射率为 2B．玻璃砖对a光的折射率为1.5C．b光的频率比a光的频率大D．b光在玻璃中的传播速度比a在玻璃中的传播速度大答案AC解析 a 光的折射率n ＝sin45°sin30°＝2，故A 对，B 错．由题图可知，a 光的偏折程度比b 光的小，所以a 光的频率小，折射率也小，由n ＝c v 可得v ＝cn ，a 光在玻璃中的传播速度比b 光的大，故C 对，D 错．3．(对全反射的理解)如图9所示，扇形AOB 为透明柱状介质的横截面，圆心角∠AOB ＝60°.一束平行于角平分线OM 的单色光由OA 射入介质，经OA 折射的光线恰平行于OB .图9(1)求该介质的折射率．(2)折射光线中恰好射到M 点的光线________(填“能”或“不能”)发生全反射． 答案 (1)3 (2)不能 解析 依题意作出光路图．(1)由几何知识可知， 入射角i ＝60°，折射角r ＝30°根据折射定律得n ＝sin isin r代入数据解得n ＝ 3(2)不能．由图中几何关系可知，射到M 点的光线的入射角θ＝30°，sin30°＝12<13，故不能发生全反射．4．(2014·新课标Ⅱ·34(2))一厚度为h 的大平板玻璃水平放置，其下表面贴有一半径为r 的圆形发光面．在玻璃板上表面放置一半径为R 的圆纸片，圆纸片与圆形发光面的中心在同一竖直线上．已知圆纸片恰好能完全遮挡住从圆形发光面发出的光线(不考虑反射)，求平板玻璃的折射率． 答案 1＋(h R －r)2解析根据全反射定律，圆形发光面边缘发出的光线射到玻璃板上表面时入射角为临界角(如图所示)设为θ，且sin θ＝1n根据几何关系得：sin θ＝Lh 2＋L 2而L ＝R －r联立以上各式，解得n ＝1＋(h R －r )2。

E D CA BH命题与证明一、选择题：（每题3分，共24分） 1、下列语句不是命题的是（ ）A 、两点之间线段最短B 、不平行的两条直线有一个交点C 、x 与y 的和等于0吗？D 、对顶角不相等。

2、命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等。

其中假命题有（ ）A 、1个B 、2个C 、3个D 、4个 3、如图，△ABC 中，︒=∠90ACB ,BE 平分∠ABC ，AB DE ⊥，垂足 为D ，如果cm AC 3=，那么DE AE +的值为（ ） A 、2㎝ B 、3㎝C 、5㎝ D 、4㎝ 4、下列各组所述几何图形中，一定全等的是（ ）A 、一个角是45°的两个等腰三角形B 、两个等边三角形C 、腰长相等的两个等腰直角三角形D 、各有一个角是40°，腰长都为5㎝的两个等腰三角形5、等腰三角形的一个外角是80°，则其底角是（ ）A 、40°B 、100°或40°C 、100°D 、806、如图，Rt △ABC 中，CD 是斜边AB 上的高，角平分线AE 交CD 于H ， EF ⊥AB 于F ，则下列结论中不正确的是（ ） A 、∠ACD=∠B B 、CH=CE=EF C 、AC=AF D 、CH=HD7、在同一平面内,两条直线可能的位置关系是（ ）A 、 平行B 、相交C 、平行或相交D 、 平行、相交或垂直 8、如图，已知AB ＝AC ，BE ＝CE ，延长AE 交BC 于D ，则图中全等三角形共有（ ）A 、1对B 、2对C 、3对D 、4对二、填空题：（每空2分，共34分）9、把命题：三角形的内角和等于180° 改写如果 ，那么 ；并找出结论 。

10、命题的定义是： 。

11、判断角相等的定理（写出2个） ， 。

12、判断线段相等的定理（写出2个） ， 。

13、写出下列假命题的反例：1） 有两个角是锐角的三角形是锐角三角形。

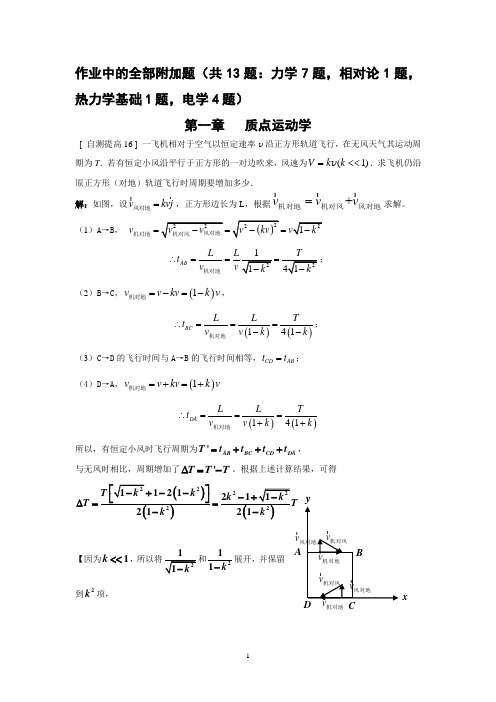
作业中的全部附加题（共13题：力学7题，相对论1题，热力学基础1题，电学4题）第一章 质点运动学[ 自测提高16 ] 一飞机相对于空气以恒定速率v 沿正方形轨道飞行，在无风天气其运动周期为T ．若有恒定小风沿平行于正方形的一对边吹来，风速为)1(<<=k k V v ．求飞机仍沿原正方形（对地）轨道飞行时周期要增加多少．解：如图，设风对地v kvj =，正方形边长为L ，根据+风对地机对地机对风v v v =求解。

（1）A →B ，机对地v ===AB L t v ∴===机对地（2）B →C ，()1机对地v v kv k v =-=-，()()141BC L L Tt v v k k ∴===--机对地； （3）C →D 的飞行时间与A →B 的飞行时间相等，CD AB t t =； （4）D →A ，()1机对地v v kv k v =+=+()()141DA L L Tt v v k k ∴===++机对地所以，有恒定小风时飞行周期为'AB BC CD DA T t t t t =+++， 与无风时相比，周期增加了'T T T ∆=-。

根据上述计算结果，可得()()221212121T k T k k ⎤--⎣⎦∆==--【因为1k <<，211k -展开，并保留到2k 项，xy A B 风对地v 机对风v 风对地v 机对风v 机对地v 机对地v得 22213112224T k T T k k ⎡⎤∆≈+++-≈⎢⎥⎣⎦】（【】中的内容可以不写）第二章 牛顿运动定律（自测提高18）一条质量分布均匀的绳子，质量为M 、长度为L ，一端拴在竖直转轴OO ′上，并以恒定角速度ω在水平面上旋转，如图2-32。

设转动过程中绳子始终伸直不打弯，且忽略重力，求距转轴为r 处绳中的张力T ( r )。

解：取距转轴为r 处，长为d r 的小段绳子，其质量为( M /L ) d r ．由于绳子作圆周运动，所以小段绳子有径向加速度，由牛顿定律得：T ( r )-T ( r + d r ) = ( M / L ) d r （ r ω2）令 T ( r )－T (r + d r ) = - d T ( r )得 d T =－( M ω2 / L ) r d r由于绳子的末端是自由端，T (L ) = 0有r r L M T Lrr T d )/(d 2)(⎰⎰-=ω 所以 )2/()()(222L r L M r T -=ω第三章 动量与角动量（自测提高13）有一水平运动的皮带将砂子从一处运到另一处，砂子经一竖直的静止漏斗落到皮带上，皮带以恒定的速率v 水平地运动．忽略机件各部位的摩擦及皮带另一端的其它影响，试问：(1) 若每秒有质量为q m =d M /d t 的砂子落到皮带上，要维持皮带以恒定速率v 运动，需要多大的功率？(2) 若q m =20 kg/s ，v ＝1.5 m/s ，水平牵引力多大？所需功率多大？解：(1) d t 时间内，有d M=q m d t 的砂子落到皮带上，速率为v ，根据动量定理，皮带作用在砂子上的力F 的冲量为：d d v d 0d v F t M M M =-⋅=⋅∴ d d m MF q t==⋅v v 由牛顿第三定律，砂子对皮带的作用力'F F =-．由于皮带匀速运动，所需的水平牵引力为'''F F F =-=，因此，所需供给的功率为：2''m m P F F q q =⋅=⋅=⋅=v v v v v(2) 当q m ＝d M/d t = 20 kg/s ，v ＝1.5 m/s 时，水平牵引力大小为 F "＝v q m =30 NO ω O ′ ω所需功率为 P= v 2q m = 45 W（註：解答的内容可适当简化些，比如说有些文字可以不写了）第四章 功与能1、（基础训练18） 半径为R ，质量为m ’，表面光滑的半球放在光滑水平面上，在其正上方放一质量为m 的小滑块。

第3章练习与思考"答案一、填空题1.定量地描述磁场在一定面积分布情况的物理量是通聖_,定量地描述磁场中各点的强弱和方向的物理量是磁感应强度B。

在均匀磁场中，它们之间的关系是①= BS。

2.用来表示物质导磁性能的物理量是磁导率H ,根据磁导率的大小，对将物质分成两类, 即非铁磁物质和铁磁物质。

3.磁场中某点的磁场强度等于该点的磁感应强度与媒介质的磁导率的比值,用公式表示为H=-oA4.铁磁材料具有高导磁性、磁饱和性和磁滞性。

5.变压器是按照电磁感应原理工作的,它的用途主要有变换电压、变换电流和变换阻抗。

6.变压器的原绕组880匝，接在220V的交流电源上，要在副绕组上得到6V电压，副绕组的匝数应是_ 24 ,若副绕组上接有3Q的电阻，则原绕组的电流为2A 。

7.变压器的损耗包插铜损和铁损两种。

8.电磁铁由励磁线圈、铁芯和衔铁三个主要部分组成。

9.汽车上使用的继电器很多，如起动继电器、喇叭继电器、闪光继电器等。

10.直流电动机是将输入的直流电能转换成机械能输出,它由立子和转子两个主要部分组成。

11 •直流电动机按励磁方式分为串励电动机、并励电动机、复励电动机和他励电动机。

12.车用起动机电枢绕组与磁场绕组的联接为串联方式。

二、判断题1 •两个形状、大小和匝数完全相同的环形螺管线圈，其一用硬纸板作芯子，另用铁芯。

当线圈通以大小相等的电流时，硬纸板和铁芯屮的磁场强度不相等。

（X ）2.变压器可以改变各种电源的电压。

（X ）3.变压器带负载运行时，当初级绕组加以额定电压后，在任何负载下，初级绕组中电流都是额定值。

（X ）4.当变圧器在额定电压和额定电流下工作时，变压器输出的有功功率就是其额定容量。

5.当电磁式继电器的线圈通电后，其动断触点打开。

（7 ）6.用万用表RxlkQ挡测量汽车点火系统中的点火线圈二次绕组阻值，若万用表指示阻值无穷大，则说明二次绕组短路。

（X ）7.流过直流电动机电枢绕组的电流为直流电。

部编版七年级下册课后练习答案〔第3、4单元〕K9阿长与《山海经》一、熟读课文,看看文章围绕阿长写了哪些事情,详写了什么,略写了什么。

从这些事情中,可以看出阿长是个什么样的人?结合课文,想一想作者为什么要写这样一个人。

设计意图:引导学生围绕中心人物梳理全文的构造层次,体会布局谋篇中的民心并根据事件中人物外在的言行,体会人物内在的品格特点;进而领会作者的写作意图,整体把握全文的主旨。

参考答案：第一局部,介绍她的身份和称呼。

第二局部,首先围绕阿长的日常言行,略写“喜欢切切察察”、对“我”过分看管,详写睡相粗俗;其次围绕阿长“满肚子是费事的礼节”详写“元旦的乖僻仪式”,略写给“我”灌输各种礼仪禁忌;再次,围绕阿长的迷信可笑详写讲长毛故事赢得“我”“空前的敬意”,略写“谋害”隐鼠而失去“我”的敬意;第三局部,围绕阿长对“我”的真诚慈祥,详写阿长为“我”买《山海经》。

从这些事情中,可以看出阿长虽然地位卑微、身世不幸,却乐天安命;虽没有文化俗、好事、迷信,却天性纯朴仁慈、仁厚慈祥阿长毫不计较“我”对她的各种不屑和无礼,真心实意关心保护“我”,努力满足我”的愿望,这让成年之后的“我”深感惭愧,同时也倍加感谢与思念。

二、这是一篇回忆童年生活的散文,作者将写作时的回忆与童年的感受彼此交织转换。

在通篇阅读、整体感知的根底上,讨论并完成以下各题1.分别找出代表“写作时的回忆”与“童年的感受”的一些语句,体会文中“成年的我”和“童年的我”两种表达视角的不同。

关于“写作时的回忆”:如“长妈妈,已经说过,是一个一向带着着我的女工,说得阔气一点,就是我的保姆”,这里“已经说过”很明显地说明作者是站在“成年的我的角度来表达;再如“此外,如今大抵忘却了,只有元旦的乖僻仪式记最清楚”,“如今”也鲜明地说明作者是站在“成年的我”的角度来表达。

关于“童年感受”:如“一到夏天,睡觉时她又伸开两脚两手,在床中间摆成一个‘大’字,挤得我没有余地翻身,久睡在一角的席子上,又已经烤得那么热。

第三、四章 生活中的数据、概率认识百万分之一·把一个绝对值大于10的数写成n a a n，的形式，其中10110<≤⨯为正整数，这就是科学计数法。

怎样用科学计数法表示绝对值较小的数（1）：确定)101(<≤a a 如：用科学计数法表示0.000000043，可以确定a=4.3 (2)：确定n ，可采用移动小数点法，即将原数的小数点右移动几位后就能得到a ，n 就取几。

例：填空（1） 将0.000 005 7用科学计数法表示为 m a 10⨯ ， 则a =________， m=________；单位换算：1米=10分米，1分米=10厘米，1厘米=10毫米； 另外规定，1毫米=1000微米，1微米=1000纳米。

学习新概念（1）精确度：利用四舍五入法取一个数的近似数时，四舍五入到哪一位，就说这个近似数精确到哪一位。

（2）有效数字：对于一个近似数，从左边第一个不是0的数字起，到精确到的数位．．．．．．止，所有的数字都叫这个数的有效数字。

例；把下列各数用科学记数学法表示： （1）0．000 000 001 65；（2）0．000 36微米，相当于多少米？（3）600纳米，相当于多少米？例2 小明量得课桌长为1.025米,请按下列要求取这个近似数:（1）四舍五入到百分位；（2）四舍五入到十分位； （3）四舍五入到个位。

补充例题1：按要求取下列各数的近似数：（1）0.00539(保留两个有效数字)；（2）349500（保留两个有效数字）。

2；判断下列近似数各有几个有效数字？并指出每个近似数的有效数字。

1、 近似数2.306；2、近似数0.02306；3、近似数0.2060 3、由四舍五入法得到的近似数1.20，精确到 位。

4、由四舍五入法得到的近似数21.3万精确到 位。

5、由四舍五入法得到的近似数3.600米精确到 位。

6、近似数0.000 000 36用科学记数法表示为 ，它精确到 位。

第三章教育与个人的发展一、单项选择题1-10 DBCABACBAC 11-20 CCDBDDCBBA21-31 CBDABCDBBCB二、多项选择题1、ABE2、ACE3、BDE4、ABCD5、ABCDE6、ABCE7、ABC8、ACE9、ACD 10、ABCD 11、ABCDE 12、BCDE 三、判断题1-8×××√××××四、填空题1、社会实践2、内在需要3、费洛伊德4、基因复制5、成熟机制6、孟子7、外铄论8、荀子9、“白板说” 10、华生 11、多因素相互作用论 12、创造性 13、阶段性 14、互补性 15、个别差异性 16、个别差异性 17、生理解剖 18、前提，可能性 19、环境 20、维果茨基 21、成熟 22、个体主观能动性 23、心理，社会 24、身体，精神 25、精神力量 26、人格 27、发展个性，个性 28、心理断乳期 29、帮助少年起飞 30、青年期 31、青年期 32、认识、价值五、名词解释1、个体身心发展：个体身心发展是指作为复杂整体的个体在从生命开始到生命结束的全部人生过程中，不断发生的变化过程，特别是指个体的身心特点向积极的方面变化的过程。

2、年龄特征：是儿童发展过程中呈现的一般的、典型的、本质的共同特征。

3、遗传素质：遗传是指从上代继承下来的生理解剖上的特点，如机体的结构、形态、感官和神经系统等的特点，也叫遗传素质。

4、成熟：在教育学中，成熟是指儿童个体生长发育的一种状况，指个体的生理和心理机能与能力都达到比较完备的阶段，即已由儿童成长发育为成人。

5、人的价值：所谓人的价值，是指人在世界中的地位得到肯定，人的作用得到发挥，人的尊严得到保证。

6、人的潜能：潜能是人区别于动物的重要标志，是能够把未成熟的人培养为成熟的人，把平凡的人培养成出色的人的可能性或前提条件。

7、发展个性：是要在人的共同性的基础上，充分把人的差别性表现出来，从而使每个人都具有自主性和独特性，实现生命的个体价值和社会价值。

第三章3-1 半径为R 、质量为M 的均匀薄圆盘上，挖去一个直径为R 的圆孔，孔的中心在12R 处，求所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量。

分析：用补偿法（负质量法）求解，由平行轴定理求其挖去部分的转动惯量，用原圆盘转动惯量减去挖去部分的转动惯量即得。

注意对同一轴而言。

解：没挖去前大圆对通过原圆盘中心且与板面垂直的轴的转动惯量为：2112J MR =① 由平行轴定理得被挖去部分对通过原圆盘中心且与板面垂直的轴的转动惯量为：2222213()()2424232c M R M R J J md MR =+=⨯⨯+⨯= ② 由①②式得所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量为：2121332J J J MR =-=3-2 如题图3-2所示，一根均匀细铁丝，质量为M ，长度为L ，在其中点O 处弯成120θ=︒角，放在xOy 平面内，求铁丝对Ox 轴、Oy 轴、Oz 轴的转动惯量。

分析：取微元，由转动惯量的定义求积分可得 解：（1）对x 轴的转动惯量为：2022201(sin 60)32Lx M J r dm l dl ML L ===⎰⎰ （2）对y 轴的转动惯量为：20222015()(sin 30)32296Ly M L M J l dl ML L =⨯⨯+=⎰（3）对Z 轴的转动惯量为：22112()32212z M L J ML =⨯⨯⨯=3-3 电风扇开启电源后经过5s 达到额定转速，此时角速度为每秒5转，关闭电源后经过16s 风扇停止转动，已知风扇转动惯量为20.5kg m ⋅，且摩擦力矩f M 和电磁力矩M 均为常量，求电机的电磁力矩M 。

分析：f M ，M 为常量，开启电源5s 内是匀加速转动，关闭电源16s 内是匀减速转动，可得相应加速度，由转动定律求得电磁力矩M 。

解：由定轴转动定律得：1f M M J β-=，即11252520.50.5 4.12516f M J M J J N m ππβββ⨯⨯=+=+=⨯+⨯=⋅ 3-4 飞轮的质量为60kg ，直径为0.5m ，转速为1000/min r ，现要求在5s 内使其制动，求制动力F ，假定闸瓦与飞轮之间的摩擦系数0.4μ=，飞轮的质量全部分布在轮的外周上，尺寸如题图3-4所示。