双语版材料力学第四章

Chapter 4 Internal Forces in BendingMECHANICS OF MATERIALS 材料力学（双语）Content§4.1 Concept of symmetrical bending and calculation sketch of the beam §4.2 The shearing force and bending moment of the beam §4.3 The shearing-force and bending-moment equations · the shearing-force and bending-moment diagrams §4.4 Relations among the shearing force、the bending moment and the density of the distributed load and their applications §4.5 Plot the bending-moment diagram by the theorem of superposition §4.6 The internal-force diagrams of the planar rigid frames and curved rods2目录§4.1 对称弯曲的概念及梁的计算简图 §4.2 梁的剪力和弯矩 §4.3 剪力方程和弯矩方程 ·剪力图和弯矩图 §4.4 剪力、弯矩与分布荷载集度间的关系及应用 §4.5 按叠加原理作弯矩图 §4.6 平面刚架和曲杆的内力图34.1 Concept of symmetrical bending and calculation sketch of the beam1. Concepts of Bending 1). BENDING(弯曲): The action of the external force or the external couple vector perpendicular to the axis of the rod makes the axis of the rod change into curve from original straight lines, this deformation is called bending. 2). BEAM（梁): The member of whose deformation is mainly bending is generally called beam.43). Practical example in engineering about bending564). Symmetric bending(平面弯曲) After deformation the curved axis of the beam is still in the same plane with the external forces. P1 q P2MThe plane of symmetry7Unsymmetrical bending： If a beam does not possess any plane of symmetry, or the external forces do not act in a plane of symmetry of the beam with symmetric planes, this kind of bending is called unsymmetrical bending.82. Calculation sketch of the beamIn general supports and external forces of the beam are very complex. We should do some necessary simplification for them for our convenient calculation and obtain the calculation sketch.1). Simplification(简化) of the beamsIn general case we take the place of the beam by its axis.2). Simplification of the loads (荷载)The loads (including the reaction) acting on the beam may be reduced into three types：concentrated force、concentrated force couple and distributed force.3). Simplification of the supports (支座条件)9①Fixed hinged support固定铰支座2 constraints，1 degree of freedom. Such as the fixed hinged support under bridges.②Movable hinged support可动铰支座1 constraint，2 degree of freedom. Such as the movable hinged support under the bridge.10θA BDB R RA A AB B B0.50.50.5P0.5PP0.50.50.5P0.5PP 0。

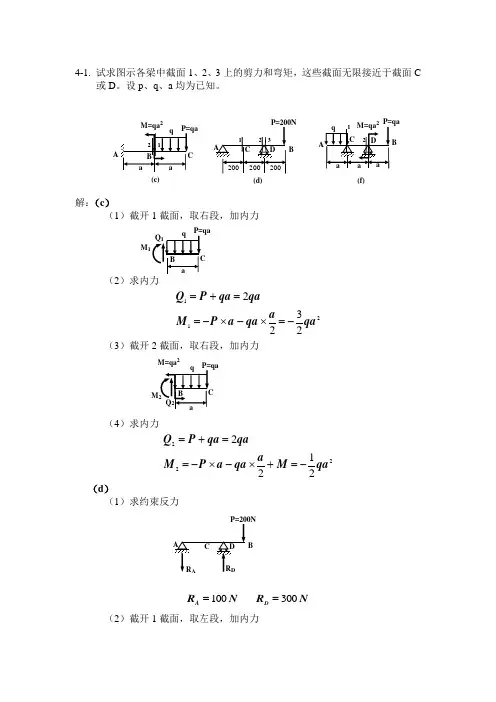
4-1. 试求图示各梁中截面1、2、3上的剪力和弯矩，这些截面无限接近于截面C或D 。

设p 、q 、a 均为已知。

解：（c ）（1）截开1截面，取右段，加内力（22112322qaa qa a P M qaqa P Q -=⨯-⨯-==+=（3）截开2截面，取右段，加内力（4）求内力2222122qaM a qa a P M qaqa P Q -=+⨯-⨯-==+=（d ）（1）求约束反力N R N R D A 300 100==（2）截开1截面，取左段，加内力(d)B(f)B(c)M=qa 2M M M=qa 2B（3）求1截面内力NmR M N R Q A A 202.010011-=⨯-=-=-=（4）截开2截面，取左段，加内力（5）求2截面内力NmR M N R Q A A 404.010022-=⨯-=-=-=（6）截开3截面，取右段，加内力（7）求3截面内力NmP M N P Q 402.020023-=⨯-===（f ）（1）求约束反力qa R qa R D C 25 21==（2）截开1截面，取左段，加内力Q 1M 12BMB（3）求1截面内力2112121 qa a qa M qa Q -=⨯-=-=（4）截开2截面，取右段，加内力（5）求2截面内力222223qa M a P M qaR P Q D -=-⨯=-=-= 4-3. 已知图示各梁的载荷P 、q 、M0和尺寸a 。

(1)列出梁的剪力方程和弯矩方程；(2)作剪力图和弯矩图；(3)确定∣Q ∣max 和∣M ∣max 。

q(c)M 0=qa 2 (d)(f)(e) (g)q(h)1BM (a)(b) Bq解：（a ）（1）求约束反力Pa M P R A A == 2（2）列剪力方程和弯矩方程⎪⎩⎪⎨⎧∈=-⨯-+⨯=∈-=+⨯=⎩⎨⎧∈=-=∈==),0[ )(2)(],0( 2)(]2,( 02)(),0( 2)(2222211111222111a x Pa a x P M x R x M a x Pa Px M x R x M a a x P R x Q a x P R x Q A A A A A A （3）画Q 图和M 图（4）最大剪力和最大弯矩值(i)q(j)BP=20kN(l)q(k)qM xxPa M P Q ==max max 2（b ）（1）求约束反力223 qa M qa R B B ==（2）列剪力方程和弯矩方程⎪⎪⎩⎪⎪⎨⎧∈-⨯-=∈-=⎩⎨⎧∈-=∈-=)2,[ )2()(],0[ 21)()2,[ )(],0[ )(2222121112221111a a x a x qa x M a x qx x M a a x qa x Q a x qx x Q （3）画Q 图和M 图（4）最大剪力和最大弯矩值2maxmax 23 qa M qa Q == （c ）（1）求约束反力qBxxqM 0=qa 2M2 2qa M qa R A A ==（2）直接画Q 图和M 图（3）最大剪力和最大弯矩值2max max 2qa M qa Q ==（d ）（1）求约束反力P R R B A == 0（2）直接画Q 图和M 图（3）最大剪力和最大弯矩值Pa M P Q ==max maxxxxx。

材料力学第4章杆件的基本变形课件第一篇：材料力学第4章杆件的基本变形课件重点：材料力学的任务，变形固体性质的基本假设难点：理解强度、刚度、稳定性的概念第4章§4.1 材料力学的任务建筑物承受荷载而起骨架作用的部分，称为结构。

组成结构或机械的单个部分则称为构件或零件。

如：桥梁的桥墩、桥面等。

每一构件都应满足一定的条件，这些条件主要是指经济与安全。

所谓经济是指构件应采用适当的材料并使截面尺寸最小（消耗最少的材料）；安全则是指构件在受力或受外界因素（如温度改变、地基沉陷等）影响时，应同时满足强度、刚度及稳定性三方面的要求。

即：安全包括三个方面：（1）足够的强度──构件具有足够的抵抗破坏的能力；（2）足够的刚度──构件具有足够的抵抗变形的能力，即要把变形控制在一定的范围内；（3）足够的稳定性──构件具有足够的保持原有平衡形式的能力。

构件在强度、刚度和稳定性三方面所具有的能力统称为构件的承载能力。

经济与安全是一对矛盾的两个方面。

而材料力学就是要解决这一矛盾，即是研究构件在各种外力或外界因素影响下的强度、刚度和稳定性的原理及计算方法的科学。

包括对材料的力学性质的研究。

这就是材料力学的任务。

§4.2 可变形固体的性质及其基本假设任何固体在外力作用下都要产生形状及尺寸的改变──即变形。

外力大到一定程度构件还会发生破坏，这种固体称为“变形固体”。

承认构件的变形，是材料力学研究问题、解决问题的基本前提。

变形包括：（1）弹性变形──外力去掉后可消失的变形；（2）塑性变形──外力去掉后不能消失的变形。

关于变形固体性质的基本假设：1．连续性假设：材料内部连续、密实地充满着物质而毫无空隙；2．均匀性假设：材料沿各部分的力学性能完全相同；3．各向同性假设：材料沿各方向的力学性能完全相同。

这样的材料称为各向同性材料，否则称为各向异性材料。

4．小变形假设：认为受力后构件的变形与其本身尺寸相比很小。

小变形包括两方面含义：（1）变形与原始尺寸在量级上进行比较，很小；（2）变形对外力的影响很小──不会显著改变外力的作用位置或不产生新的外力成分。

材料力学双语教学学习资料第一章绪论Chapter 1 Introduction§1-1 材料力学的任务The Tasks of Mechanics of Materials1＊. 材料力学: Mechanics of Materials2. 构件: Structural Members3. 变形: Deformation4＊. 强度: Strength5＊. 刚度: Rigidity6＊. 稳定性: Stability§1-2 变形固体的基本假设Fundamental Assumptions of SolidDeformation Bodies1. 连续性假设: Continuity2. 均匀性假设: Homogeneity3. 各向同性假设: Isotropy§1.3 外力及其分类External Forces and Classification1. 分布力: Distributed Force2. 集中力: Point Force3. 静载荷: Static Load4. 动载荷: Dynamic Load§1.4 内力、截面法和应力的概念Concepts of Internal Forces，Method ofSection and Stress1＊. 内力: Internal Force2＊. 截面法: Method of Section3. 截面法的三个步骤：截开，代替，平衡Three steps of method of section: cut off, substitute , and equilibrium.4＊. 应力: Stress5. 平均应力：Average stress6. 应力（全应力）：Whole stress（sum stress）7＊. 正应力: Normal Stress8＊. 剪应力(切应力)：Shearing Stress§1.5 变形与应变Deformation and Strain1．线应变: Strain2．剪应变: Shearing Strain§1.6 杆件变形的基本形式Basic Types of Deformations of Rods1＊. 拉伸或压缩: Tension or Compression2＊. 剪切: Shear3＊. 扭转: Torsion4＊. 弯曲: Bending第二章拉伸、压缩与剪切Chapter 2 Tension，Compression andShear§2.1 轴向拉伸与压缩的概念和实例The Concept and Examples of AxialTension and Compression1. 拉杆: Tensile Rod2. 压杆: Compressive Rod3. 受力特点：外力合力的作用线与杆轴线重合Characteristic of the External Forces: The acting line of the resultant of external forces is coincided with the axis of the rod.4. 变形特点：杆沿轴向伸长或缩短Characteristic of Deformation: Rod will elongate or contract along the axis of the rod.§2.2 轴向拉伸或压缩时横截面上的内力和应力Internal Force and Stress of Axial Tension or Compression on the Cross Section1＊. 横截面: Cross Section2＊. 轴力: Normal Force3＊. 轴力图: Diagram of Normal Force§2.3 直杆轴向拉伸或压缩时斜截面上的应力Stress of Axial Tension or Compressionon the Skew Section1. 斜截面: Skew Section2.ασσα2cos = αστα2s i n 2=§2.4 材料在拉伸时的力学性能Mechanical Properties of Materialswith Tensile Load1. 标准试件: Specimen2. 低碳钢(C ≤0.3%): Low Carbon Steel3. 弹性阶段:Elastic Region4. 屈服阶段:Yielding Stage5. 强化阶段:Hardening Stage6. 颈缩阶段: Necking Stage 7＊.σp ----比例极限: Proportional Limit 8＊.σe ----弹性极限: Elastic Limit 9＊.σs ----屈服极限: Yielding Stress 10＊.σb ----强度极限: Ultimate Stress 11. 延伸率: Percent Elongation12. 断面收缩率: Percent Reduction of Area 13. 塑性材料: Ductile Materials 14. 脆性材料: Brittle Materials 15. 铸铁:Cast iron§2.7 失效、安全系数和强度计算 Failure, Safety factor and Strengthcalculation1＊. 许用应力: Allowable Stress 2. 安全系数: Safety Factor 3＊. 强度条件: Strength Condition][max σσ≤=AF N4＊. 强度校核: Check strength][max σσ≤5＊. 截面设计: Section design][σNF A ≥6＊. 确定许可载荷:Determine allowable load][σA F N ≤§2.8 轴向拉伸或压缩时的变形 Deformation in Axial Tension orCompression1. 弹性变形: Elastic Deformation2. 塑性变形: Plastic Deformation3. 纵向应变: Longitudinal Strainll l l l -=∆=1ε 4. 横向应变: Lateral Straindd d d d -=∆=''ε5．线弹性变形:Linear Elastic Deformation6.泊松比:Poisson’s ratioεεμ'=7＊.弹性模量-E ：表示材料抵抗拉压变形的 能力 E - modulus of elasticity ：Indicates the capability of materials for resisting tension or compression 8＊.抗拉刚度-EA :表示构件抵抗拉压变形的能力EA -the axial rigidity: Indicates the capability of constructive members for resisting tension or compression 9＊. 胡克定律（Hooke’s Law ）:当应力不超过材料的比例极限时，应力与应变成正比.The stress is proportional to the strain within the elastic region.εσE =§2.12 应力集中的概念The Concept of Stress Concentration 1.由于截面尺寸的突然变化，使截面上的应力分布不再均匀，在某些部位出现远大于平均值的应力，称应力集中。