函数的最大值和最小值

函数的最大值与最小值在数学中，函数的最大值和最小值是非常重要的概念。

最大值指的是函数在某个区间上取得的最大数值，而最小值则是函数在该区间上取得的最小数值。

求解函数的最大值和最小值在实际问题中具有重要的应用，如寻找最佳解、优化问题等。

本文将介绍如何求解函数的最大值和最小值，并探讨其中的相关概念和方法。

一、局部最值和全局最值函数的最大值和最小值可以分为局部最值和全局最值两种情况。

局部最值指的是函数在某个小区间内取得的最大或最小值，而全局最值则是函数在整个定义域上取得的最大或最小值。

为了更好地理解这两个概念，我们考虑一个简单的例子。

假设有一个函数f(x) = x^2，在闭区间[-1, 1]上进行观察。

当x为-1时，f(-1) = 1；当x为0时，f(0) = 0；当x为1时，f(1) = 1。

可以看出，函数f(x)在这个区间内的最大值和最小值分别为1和0。

因此，在这个例子中，最大值和最小值都是局部最值。

然而，如果我们考虑函数f(x)在整个定义域上的取值情况，就会发现函数f(x)在x等于0时取得了全局最小值0。

因此，全局最值并不一定出现在局部最值处。

二、求解最值的方法在求解函数的最大值和最小值时，有一些常用的方法和技巧。

1. 导数法导数法是一种常见且经典的求解最值的方法。

它基于一个重要的数学定理：在函数的极值点处，导数等于0。

假设有一个定义在区间[a, b]上的函数f(x)，我们想要求解在该区间上的最大值和最小值。

首先，我们可以计算出函数f(x)的导数f'(x)。

然后，我们找到f'(x) = 0的所有解，这些解即为函数f(x)的极值点。

接下来，我们需要判断这些极值点是函数的最大值还是最小值。

可以通过一些判定条件进行判断，如利用二阶导数的符号、导数的变化规律等。

2. 区间法区间法在求解最值时，将区间等分成多个小区间，然后计算函数在每个小区间的取值，并找出最大值和最小值。

具体做法是将区间[a, b]等分成n个小区间，每个小区间的长度为Δx = (b - a) / n。

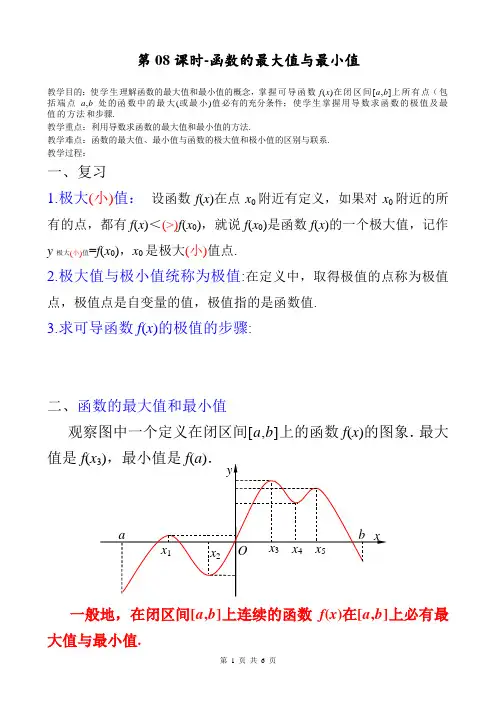
第08课时-函数的最大值与最小值教学目的：使学生理解函数的最大值和最小值的概念，掌握可导函数f(x)在闭区间[a,b]上所有点（包括端点a,b处的函数中的最大(或最小)值必有的充分条件；使学生掌握用导数求函数的极值及最值的方法和步骤.教学重点：利用导数求函数的最大值和最小值的方法.教学难点：函数的最大值、最小值与函数的极大值和极小值的区别与联系.教学过程：一、复习1.极大(小)值：设函数f(x)在点x0附近有定义，如果对x0附近的所有的点，都有f(x)＜(>)f(x0)，就说f(x0)是函数f(x)的一个极大值，记作y极大(小)值=f(x0)，x0是极大(小)值点.2.极大值与极小值统称为极值:在定义中，取得极值的点称为极值点，极值点是自变量的值，极值指的是函数值.3.求可导函数f(x)的极值的步骤:二、函数的最大值和最小值观察图中一个定义在闭区间[a,b]上的函数f(x)的图象．最大值是f(x一般地，在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值.说明：(1)在开区间(a ,b )内连续的函数f (x )不一定有最大值与最小值．如函数f (x )=x 1在(0,+∞)内连续，但没有最大值与最小值；(2)函数的最值是比较整个定义域内的函数值得出的；函数的极值是比较极值点附近函数值得出的.(3)函数f (x )在闭区间[a ,b ]上连续，是f (x )在闭区间[a ,b ]上有最大值与最小值的充分条件而非必要条件.(4)函数在其定义区间上的最大值、最小值最多各有一个，而函数的极值可能不止一个，也可能没有一个.三、例题选讲： 利用导数求函数的最值例1：求下列函数在相应区间上的最大值与最小值. (1) y =x 4-2x 2+5，x ∈[-2,2]；(2)x x x f sin 21)(+=，x ∈]2,0[π(1)解：先求导数，得x x y 443/-=令/y ＝0即0443=-x x 解得1,0,1321==-=x x x导数/y 的正负以及)2(-f ，)2(f 如下表从上表知，当时，函数有最大值13，当时，函数有最小值4 .小结：利用导数求函数的最值步骤:由上面函数f (x )的图象可以看出，只要把连续函数所有的极值与定义区间端点的函数值进行比较，就可以得出函数的最值了.设函数f (x )在[a ,b ]上连续，在(a ,b )内可导，则求f (x )在[a ,b ]上的最大值与最小值的步骤如下： (1)求f (x )在(a ,b )内的极值；(2)将f (x )的各极值与f (a )、f (b )比较得出函数f (x )在[a ,b ]上的最值.练习：求下列函数的值域：（1）]4,0[,)2()1(22∈--=x x x y ； （2）]4,2[,2122-∈-+=x x xy ；（3）)10(3)(3≤≤+-=x ax x x f （a 为常数）.例2：已知动点M 在抛物线y 2=2px (p >0)上，问M 在何位置时到定点P (p ,p )的距离最短.练习：动点P(x,y)是抛物线y=x2-2x-1上的点，O为原点，设S=|OP|2，求S的最小值.例3：已知x,y为正实数，且满足关系式x2-2x+4y2=0，求x⋅y 的最大值.例4：已知抛物线y= -x2+2，过其上一点P引抛物线的切线l，使l与两坐标轴在第一象限围成的三角形的面积最小，求l的方程.小结：⑴函数在闭区间上的最值点必在下列各种点之中：导数等于零的点，导数不存在的点，区间端点；⑵函数f(x)在闭区间[a,b]上连续，是f(x)在闭区间[a,b]上有最大值与最小值的充分条件而非必要条件；⑶闭区间[a,b]上的连续函数一定有最值；开区间(a,b)内的可导函数不一定有最值，若有唯一的极值，则此极值必是函数的最值.例5：设a ∈R ，函数f (x )=x 2e 1-x -a (x -1)．(1)当a =1时，求f (x )在⎝⎛⎭⎪⎪⎫34，2内的极大值； (2)设函数g (x )=f (x )+a (x -1-e 1－x )，当g (x )有两个极值点x 1，x 2(x 1<x 2)时，总有x 2g (x 1)≤λf '(x 1)，求实数λ的值．(其中f '(x )是f (x )的导函数)．[解] (1)当a ＝1时，f (x )＝x 2e 1－x －(x －1)，则f '(x )＝(2x －x 2)e 1－x－1＝(2x －x 2)－e x －1e x －1， 令h (x )＝(2x －x 2)－e x －1，则h '(x )＝2－2x －e x －1，显然h '(x )在⎝⎛⎭⎫34，2内是减函数，又h ′⎝⎛⎭⎫34＝12－14e<0，故x ∈⎝⎛⎭⎫34，2时，总有h '(x )<0，所以h (x )在⎝⎛⎭⎫34，2内是减函数．又h (1)＝0，所以当x ∈⎝⎛⎭⎫34，1时，h (x )>0，从而f '(x )>0，这时f (x )单调递增，当x ∈(1,2)时，h (x )<0，从而f '(x )<0，这时f (x )单调递减，所以f (x )在⎝⎛⎭⎫34，2内的极大值是f (1)＝1.(2)由题可知g (x )＝(x 2－a )e 1－x ，则g '(x )＝(2x －x 2＋a )e 1－x ＝(－x 2＋2x ＋a )e 1－x .根据题意，方程－x 2＋2x ＋a ＝0有两个不同的实根x 1，x 2(x 1<x 2)， 所以Δ＝4＋4a >0，即a >－1，且x 1＋x 2＝2， 因为x 1<x 2，所以x 1<1.由x 2g (x 1)≤λf ′(x 1)，其中f ′(x )＝(2x －x 2)e 1－x －a ，可得(2－x 1)(x 21－a )e1－x 1≤λ[(2x 1－x 21)e 1－x 1－a ]，注意到－x 21＋2x 1＋a ＝0，所以上式化为(2－x 1)(2x 1)e 1－x 1≤λ[(2x 1－x 21)e 1－x 1＋(2x 1－x 21)]，即不等式x 1[2e 1－x 1－λ(e 1－x 1＋1)]≤0对任意的x 1∈(－∞，1)恒成立．①当x 1＝0时，不等式x 1[2e 1－x 1－λ(e 1－x 1＋1)]≤0恒成立，λ∈R ；②当x 1∈(0,1)时，2e 1－x 1－λ(e 1－x 1＋1)≤0恒成立，即λ≥2e 1－x 1e 1－x 1＋1，令函数k (x )＝2e 1－x e 1－x ＋1＝2－2e 1－x ＋1，显然，k (x )是R 上的减函数，所以当x ∈(0,1)时，k (x )<k (0)＝2e e ＋1，所以λ≥2ee ＋1；③当x 1∈(－∞，0)时，2e 1－x 1－λ(e 1－x 1＋1)≥0恒成立，即λ≤2e 1－x 1e 1－x 1＋1，由②，当x ∈(－∞，0)时，k (x )>k (0)＝2e e ＋1，所以λ≤2ee ＋1.综上所述，λ＝2ee ＋1.作业布置：完成《全品》练习册P15-16完成《全品》单元测评（一）A。

函数最大值最小值函数的最大值和最小值是函数分析中的重要概念。

在数学和科学领域，函数最大值和最小值的确定经常用于解决实际问题。

在这篇文章中，我们将探讨函数最大值和最小值以及它们在数学和科学中所起的重要作用。

让我们来了解什么是函数最大值和最小值。

在数学中，函数的最大值和最小值是指函数在定义域内的最大和最小值。

换句话说，当一个函数在定义域内达到其最大值或最小值时，我们称该函数具有最大值或最小值。

这些点称为函数的极值点。

在数学中，函数的最大值和最小值可以用求导数来求解。

求导数是函数的导数，它代表了函数在某一点的斜率。

函数的最大值和最小值出现在导数为零或不存在的点。

这些点称为函数的临界点。

通过对函数求导并找到所有临界点，我们可以确定函数的最大值和最小值。

在科学领域，函数的最大值和最小值有很多应用。

例如，在物理学中，通过确定物体的运动方程式，可以确定运动物体的最大高度和最小速度。

在经济学中，通过确定收入函数，可以确定财务分析中的最大利润和最小成本。

在生物学中，函数的最大值和最小值可以用于确定生物体的最佳生长条件。

通过确定生物体的生长率函数，可以确定生物体的最适生长条件。

这些条件可以通过确定生物体的最大值和最小值来确定。

在计算机科学中，函数的最大值和最小值可以用于确定算法的最大效率和最小时间。

通过确定算法的最大值和最小值，可以确定最优解决方案。

这些解决方案可以通过找到函数的最大值和最小值来确定。

函数的最大值和最小值是数学和科学中的重要概念。

它们可以用于解决各种实际问题，如物理学、经济学、生物学和计算机科学中的问题。

通过确定函数的最大值和最小值，可以确定最优解决方案。

因此，了解和应用函数的最大值和最小值对于解决实际问题至关重要。

求函数最大值最小值的方法
求函数的最大值和最小值可以通过7种方法：1、配方法；2、判别式法；
3、利用函数的单调性；
4、利用均值不等式；
5、换元法；
6、数形结合法；
7、利用导数求函数最值。

1、配方法：形如的函数，根据二次函数的极值点或边界点的取值确定函数的最值。

2、判别式法：形如的分式函数，将其化成系数含有y的关于x的二次方程。

由于，所以≥0，求出y的最值，此种方法易产生增根，因而要对取得最值时对应的x值是否有解检验。

3、利用函数的单调性：首先明确函数的定义域和单调性，再求最值。

4、利用均值不等式，形如的函数，注意正、定等的应用条件，即：a，b均为正数，是定值，a=b的等号是否成立。

5、换元法：形如的函数，令，反解出x，代入上式，得出关于t的函数，注意t的定义域范围，再求关于t的函数的最值。

还有三角换元法，参数换元法。

6、数形结合法：形如将式子左边看成一个函数，右边看成一个函数，
在同一坐标系作出它们的图象，观察其位置关系，利用解析几何知识求最值。

求利用直线的斜率公式求形如的最值。

7、利用导数求函数最值。

中考知识点函数的最大值与最小值函数的最大值和最小值是中考数学中的一个重要知识点。

在解题过程中，我们需要运用一些方法来求解函数的最大值和最小值。

本文将介绍三种常见的方法：图像法、导数法和附加条件法，以帮助大家更好地理解和应用这一知识点。

一、图像法使用图像法求解函数的最大值和最小值，一般需要绘制函数的图像。

在中考中，我们通常采用手绘图像的方式进行计算。

下面以一个例题来说明图像法的具体步骤。

例题：已知函数$f(x)=x^2-6x+5$，求$f(x)$的最大值和最小值。

解题步骤：（1）首先，我们绘制出函数$f(x)=x^2-6x+5$的图像。

为了方便计算，我们可以计算出函数的顶点坐标。

由二次函数的性质可知，函数的顶点坐标为$(p,q)$，其中$p$的值等于二次项系数的相反数的一半，$q$的值等于函数在$p$处的取值。

可以求得顶点坐标为$p=3$，$q=-4$。

将这个顶点坐标标在函数图像上。

（2）根据图像，我们可以看出函数$f(x)$的最大值为$q=-4$，对应的$x$值为$p=3$；最小值为$q=-\infty$（无穷小），对应的$x$值为$x\to \infty$。

因此，函数$f(x)=x^2-6x+5$的最大值为$-4$，最小值为$-\infty$。

二、导数法使用导数法求解函数的最大值和最小值，可以利用函数的导数来判断函数的增减性。

下面以一个例题来说明导数法的具体步骤。

例题：已知函数$g(x)=3x^2+4x+2$，求$g(x)$的最大值和最小值。

解题步骤：（1）首先，我们需要求出函数$g(x)$的导函数$g'(x)$。

对于一次或二次函数，我们可以通过对函数的表达式进行求导来得到导函数。

对函数$g(x)$进行求导，得到$g'(x)=6x+4$。

（2）根据导数的定义，导数表示函数在某一点的变化率。

根据函数的导数可以判断函数的增减性。

当导数大于$0$时，函数递增；当导数小于$0$时，函数递减。

最大值函数和最小值函数首先，我们来介绍最大值函数。

最大值函数是指输入一组数或一个函数集合，输出它们中的最大值。

在数学上，最大值函数可以用如下形式表示：f(x₁, x₂, ..., xₙ) = max{x₁, x₂, ..., xₙ}其中，x₁,x₂,...,xₙ是一组实数。

最大值函数的输出是输入数列或函数集合中的最大值。

举个例子，假设有一组数{x₁,x₂,...,xₙ}，其中x₁=1,x₂=4,x₃=6,x₄=2，那么最大值函数可以表示为：f(x₁, x₂, x₃, x₄) = max{1, 4, 6, 2} = 6这个函数的输出是数列中的最大值6接下来，我们来介绍最小值函数。

最小值函数类似于最大值函数，不同之处在于它输出的是数列或函数集合中的最小值。

在数学上，最小值函数可以用如下形式表示：g(x₁, x₂, ..., xₙ) = min{x₁, x₂, ..., xₙ}同样，x₁,x₂,...,xₙ是一组实数。

最小值函数的输出是输入数列或函数集合中的最小值。

继续以上面的例子，我们可以得到最小值函数：g(x₁, x₂, x₃, x₄) = min{1, 4, 6, 2} = 1这个函数的输出是数列中的最小值1最大值函数和最小值函数在数学中的应用十分广泛。

在数列分析中，我们经常需要找到数列中的最大值或最小值，以此来描述数列的特性。

例如，在股票市场中，我们可能需要找到只股票在一段时间内的最高价格和最低价格，这样可以帮助我们判断该股票的波动情况和投资风险。

在优化问题中，最大值函数和最小值函数也起到了关键作用。

例如，在线性规划中，我们需要定义目标函数并找到使其最大化或最小化的变量取值，从而求解最优解。

最大值函数和最小值函数可以帮助我们准确定义目标函数，并找到最优解。

在数据分析中，最大值函数和最小值函数常常用于寻找极端值。

通过求解数据集的最大值和最小值，我们可以获得数据集中的异常值或重要特征。

例如，在气象学中，我们可以通过求解气象数据中的最高温度和最低温度，推测地的气候情况和季节变化。

函数的最大值和最小值教学内容：本节课主要讲解函数的最大值和最小值的概念，以及如何求解函数的最大值和最小值。

教学目标：1. 理解函数的最大值和最小值的概念。

2. 学会使用图像法求解函数的最大值和最小值。

3. 学会使用导数法求解函数的最大值和最小值。

教学准备：1. 教学课件。

2. 练习题。

教学过程：一、导入（5分钟）1. 引入函数的最大值和最小值的概念。

2. 举例说明函数的最大值和最小值的意义。

二、函数的最大值和最小值的概念（10分钟）1. 讲解函数的最大值和最小值的定义。

2. 给出函数的最大值和最小值的判定条件。

三、图像法求解函数的最大值和最小值（10分钟）1. 讲解图像法求解函数的最大值和最小值的方法。

2. 举例说明图像法求解函数的最大值和最小值的步骤。

四、导数法求解函数的最大值和最小值（10分钟）1. 讲解导数法求解函数的最大值和最小值的方法。

2. 举例说明导数法求解函数的最大值和最小值的步骤。

五、练习题讲解（10分钟）1. 讲解练习题的解题思路。

2. 逐个解答学生提出的疑问。

教学反思：本节课通过讲解函数的最大值和最小值的概念，以及如何求解函数的最大值和最小值，使学生掌握了这一重要知识点。

在教学过程中，采用图像法和导数法两种方法进行讲解，使得学生能够更好地理解和运用。

通过练习题的讲解，巩固了学生所学的知识，并解答了学生提出的疑问。

总体来说，本节课的教学效果较好，学生对函数的最大值和最小值的概念和求解方法有了较为深入的理解。

但在教学过程中，仍需注意引导学生主动思考和探索，提高学生的学习兴趣和参与度。

六、案例分析：实际问题中的最大值和最小值（10分钟）1. 引入实际问题，如成本最小化、收益最大化等。

2. 展示如何将实际问题转化为函数的最大值和最小值问题。

3. 引导学生运用所学的图像法和导数法解决实际问题。

七、练习与讨论：小组合作求解复杂函数的最大值和最小值（15分钟）1. 分配练习题，要求学生以小组合作的形式进行求解。