第九讲(1)-机器人动力学--拉格朗日方程
- 格式:pdf
- 大小:516.50 KB
- 文档页数:24


四足机器人动力学建模:拉格朗日动力学引言在机器人领域中,四足机器人是一种常见的机器人类型。
它们具有四条腿和能够模拟和模仿动物行走的能力。
为了实现自主步行和平稳运动,我们需要对四足机器人的动力学进行建模和分析。
本文将介绍使用拉格朗日动力学方法对四足机器人进行建模的过程和步骤。
拉格朗日动力学简介拉格朗日动力学是一种描述系统动力学行为的方法。
它基于拉格朗日原理,通过最小化系统的运动方程,求解系统中的广义坐标和约束力。
在机器人动力学中,拉格朗日动力学方法被广泛应用于建模和控制。
四足机器人动力学建模步态与坐标系在进行四足机器人动力学建模之前,首先需要确定机器人的步态和坐标系。
通常,四足机器人的步态可以分为步行和跑步两种模式。
对于步行模式,机器人的步态可以简化为前后左右四个联系稳定的点。
在这种情况下,机器人的坐标系可以选择为正前方为x轴正方向,右侧为y轴正方向,地面为z轴正方向。
运动学分析在进行动力学建模之前,需要进行机器人的运动学分析。
运动学分析可以得到机器人各个关节的位置、速度和加速度信息。
这些信息对于后续的动力学建模非常重要。
动力学建模操作要素在进行动力学建模之前,需要确定机器人系统的操作要素。
这些要素包括机器人的质量、惯性、关节约束等。
通过对这些要素的分析和建模,可以得到机器人的整体动力学方程。
拉格朗日方程拉格朗日动力学方法使用拉格朗日方程来描述系统的运动方程。
拉格朗日方程可以通过系统的动能和势能表达式得到。
对于四足机器人,为了简化模型,通常可以假设机器人为刚体,并且忽略其柔软特性。
拉格朗日方程的形式如下:L = T - V其中,L为拉格朗日函数,T为系统的动能,V为系统的势能。
动力学模拟通过对拉格朗日方程进行求解,可以得到系统的运动方程。
为了模拟机器人的动力学行为,可以使用数值方法进行迭代求解。
常见的数值方法有欧拉法和中点法等。
结论通过拉格朗日动力学方法进行建模,可以得到四足机器人的运动方程和动力学模拟。





机器人学第九讲动力学及仿真实践黄之峰副教授广东工业大学2019-07-03主要内容:1,正逆动力学的意义2,逆动力学分析•拉格朗日法•牛顿欧拉法3,正动力学仿真•单位矢量法23机器人动力学是研究机器人的运动和作用力之间的关系。
机器人动力学的用途:机器人的最优控制:优化性能指标和动态性能,调整伺服增益;设计机器人:算出实现预定运动所需的力/力矩;机器人的仿真:根据连杆质量、负载、传动特征的动态性能仿真机器人是一个具有多输入和多输出的复杂动力学系统,存在严重的非线性,需要非常系统的方法来处理。
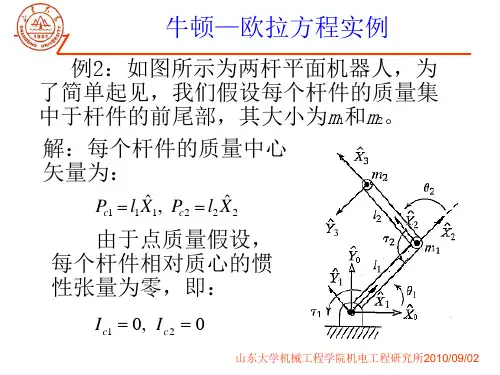
θ2θ1l 1l 2m 1m 2•逆动力学:机器人设计关节动力源选型。
前馈控制实现更好的轨迹跟踪。
正动力学数值计算•正动力学动力学仿真,评价及优化控制增益5用拉格朗日法建立机器人动力学方程的步骤1.选取坐标系,选定完全独立的广义关节变量2.选定相应关节上的广义力:当为位移变量时,则为力;当是角度变量时,则为力矩。
3.求出机器人各个构件的动能和势能,构造拉格朗日函数。
4.代入拉格朗日方程求得机器人系统的动力学方程),,2,1(n i q i i F i q i F i q 9θ2θ1l 1l 2m 1m 2p 2222y xθ2θ1l 1l 2m 1m 2θ2θ1l 1l 2m 1m 2θ2θ1l 1l 2m 1m 2θ2θ1l 1l 2m 1m 2θ2θ1l 1l 2m 1m 2θ2θ1l 1l 2m 1m 2θ2θ1l 1l 2m 1m 2θ2θ1l 1l 2m 1m 2θ2θ1l 1l 2m 1m 2常用的简化策略:1.当杆件质量不很大,重量很轻时,动力学方程中的重力项可以忽略。
2.当关节速度不很大,机器人不是高速机器人时,含向心力项,哥式力项等可以省略。
3.当关节加速度不很大,也就是关节电机的加减速不是很突然时,含有的项有可能给予省略,但是会影响机器人的循环作业时间。
21, 20θ2θ1l 1l 2m 1m 2p 2θ2θ1l 1l 2m 1mx y 0ˆ思考:酉矩阵的性质?ˆˆ T绕原点转思考1:匀速运动物体的角动量是否恒定?对于连续刚体则有:R刚体的运动分为相对于自身质心的转动以及质心的平动,这里指的标准姿态下的转动惯量是指相对于质心来计算的。


拉格朗日方程(Lagrange's equations)和虚功原理(Principle of Virtual Work)都是理论力学中常用的分析方法,用于描述物体的运动和力学系统的行为。
拉格朗日方程是描述质点或物体在广义坐标下的运动的方程。
它是源自哈密顿原理(Hamilton's principle),通过定义一个称为拉格朗日量(Lagrangian)的函数来推导得到。
拉格朗日量是系统动能与势能的差,其定义为L = T - V,其中T 是动能,V 是势能。
拉格朗日方程可以统一描述多自由度系统中质点或刚体的运动,通过求解其中的偏微分方程可以得到物体的运动方程。
虚功原理是一个广义的力学原理,用于分析力学系统中的约束。
它通过平衡约束力和虚位移所作的虚功为零来得到系统的运动方程。
虚功原理要求系统在一组虚位移下保持等势,即满足约束条件。
通过应用虚功原理,可以推导出与拉格朗日方程等价的运动方程。
虚功原理和拉格朗日方程都是建立在能量守恒原理的基础上,它们提供了一种简洁而深入的方法来描述物体的运动和约束行为。
它们在理论力学、动力学、弹性力学等领域具有重要的应用价值。
拉格朗日方程(Lagrange's equations)给出了描述力学系统中物体运动的一阶微分方程。
在一般的情况下,拉格朗日方程可以表示为:d/dt (∂L/∂ᶲ̇ᵢ) - ∂L/∂ᶲᵢ = Qᵢ其中,L 是系统的拉格朗日量,ᶲ是广义坐标(generalized coordinates),ᶲ̇是对应的广义速度(generalized velocities),Qᵢ是外力对应的广义力(generalized forces)。
在使用拉格朗日方程求解力学系统时,我们首先选择适当的广义坐标,构建系统的拉格朗日量。
然后,对拉格朗日量分别对广义速度和广义坐标求偏导,并对时间求导,得到上述方程中的项。
最后,根据外力对应的广义力,求解该方程可以得到系统的运动方程。
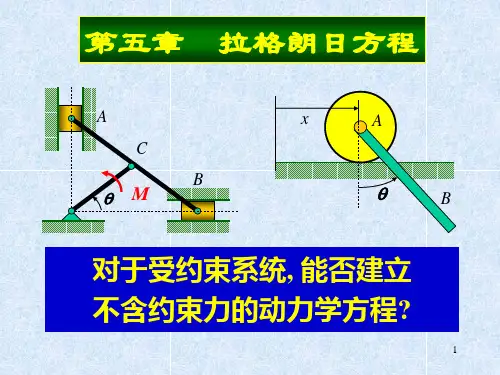
二、拉格朗日方程及其应用虽然可以直接用牛顿第二定律或达朗贝尔原理建立多自由度系统的运动微分方程,但是在许多情况下应用拉格朗日方程法更为方便。
这里用最简单的方式推导拉格朗日方程,以便更好地理解这个被广泛应用的方程的意义。
我们知道,对于一能量守恒的系统,系统的动能和势能的总和是不变的,因此,它们的总和对时间的导数等于零,即:式中:是系统的动能,它是系统广义速度的函数;是系统的势能,它是系统广义坐标的函数。
下面将说明,这两者分别可以用广义坐标和广义速度的二次型表示。
单自由度系统的动能和势能公式如下:这个结论可以推广到多自由度系统。
如下图4-6,使系统各质点产生位移,则在处的力为(a)设系统有个力作用,则系统总势能为:(b)把公式(a)代入(b)中,得:(c)若用矩阵符号,上式可写成:若把改为更一般的广义坐标符号,上式变为:(d)上式就是用广义坐标和刚度矩阵的二次型表示的系统势能表达式。
若以表示质量的速度,可以仿照单自由度系统动能的方法表示多自由度系统的动能:或写成矩阵形式:我们假设系统的动能只与广义速度有关而与广义坐标无关,对微振动这是成立的。
下面来推导拉格朗日方程。
为此,对进行全微分:(e)将对求导,有:将上式乘以并对从到求和,有:(f)比较(a),(f)两式可知:(g)对(g)进行一次微分,得(h)(h),(e)两式相减可得:根据守恒系统的原理,有(i)因为个广义坐标是独立的,不可能都等于零,因此要上式成立必须使(j)当系统还作用有除有势力之外的附加力时, 外力在上所作的功将是令,则可得:(4-8)式中是除有势力之外的所有外力,其中包括阻尼力,阻尼力可表示为:(4-9)。
物理学中的拉格朗日方程:理论的优美和实践的应用拉格朗日方程(Lagrange's equation)是物理学中一种重要的数学工具和思维模型,以其优美的形式和兼具理论和实践特性的普适性被广泛应用于众多领域,尤其是研究动力学、力学、相对论等方面。
本文将探讨拉格朗日方程的概念、原理、应用和意义,从理论和实践两个角度考察其的普适性与现实意义。
一、拉格朗日方程的概念与原理拉格朗日方程的概念最初由18世纪意大利数学家拉格朗日(Lagrangian)提出,用来描述系统在不同时间下的状态和运动。
它是一种基于哈密顿原理和变分法的数学表达式,通过用一组广义坐标表示系统的状态和动力学能量,建立了由广义坐标和其导数和得出的拉格朗日量与广义坐标和其导数的偏导进行微分运算,从而推得该系统的运动方程。
其中拉格朗日量是用来描述系统的状态和运动的重要参数,同时也是哈密顿量(传统力学领域的主要参数之一)的一个函数。
拉格朗日方程的应用基于动力学的基本原理和力学的两个基本定理:牛顿第二定律和能量守恒定律。
根据牛顿第二定律F=ma,可将系统中的受力作用表示为关于加速度、质量和力的积,再通过逐步推导,得出与使用牛顿第二定律相同的运动方程。
另一方面,能量守恒定律表明一个系统的总能量(包括动能和势能)在运动中保持不变,因此可以通过拉格朗日量的表达式,建立出系统的能量守恒方程。
二、拉格朗日方程的应用和意义拉格朗日方程作为动力学和力学的重要数学工具和思维模型,被广泛应用于相对论、天体力学、流体力学、电动力学等许多物理学领域。
其中,最为广泛应用的是新的相对论动力学,它通过拉格朗日方程描述质点或场在时空中的运动和相互作用,推导出等效于牛顿经典力学的运动方程。
同时,拉格朗日方程以其优美的形式和适用性,也很好地体现了物理学的本质和思想。
正如法国科学家朗之万所说“我们可以同样完全否认哈密顿的表达式,因为它并不是物理本质的表达方式。
拉格朗日的表达式,则是优美的物理思想。