机械可靠性设计(应力强度干涉模型)
- 格式:ppt
- 大小:575.50 KB
- 文档页数:33







机械零件强度可靠性设计的简单数学分析—《数学文化》的读书报告徐华超机设8班,2009302349摘要 我们都知道传统的设计方法是把设计变量当做确定性变量来看待。
但是对于一大批同类产品总任何特定的一件来讲,许多设计变量(例如工作载荷,极限应力,零件尺寸等)都是随机变量。
如果在产品的设计过程中通过概率与统计的方法来分析和处理这些随机变量,则可以更为准确的把握产品的可靠性。
基于上述思想及相应的方法进行对机械零件强度可靠性设计中变量分析,可以确定产品在规定的工作条件下及规定的使用期限内完成规定功能的概率,这一概率就是反应产品可靠性的定量指标之一。
关键词 应力 概率密度函数 正态分布 引言可靠性作为产品的一个重要的质量指标特征,它表示产品在规定的工作条件下及规定的使用期限内完成规定功能的能力。
在现实中可靠性好可以有效的在规定的时间内完成功能,对产品的安全性,口碑和性价比起到至关重要的作用!在设计产品中所遇到的各种变量采用概率和统计的方法来分析和处理,可以较为准确的把握产品的可靠性。
机械零件的概率设计和相应的可靠度计算是机械可靠性设计的一项重要内容,下面就机械强度的可靠度计算方法做一阐述。
(一)基本概念及公式如果广义的讲,可以把一切引起失效的外部作用的参数叫做应力,而把零件本身抵抗失效的能力叫做强度,则通过判断应力是否超过强度就可以判断零件的安全性。
若将应力和强度视为随机变量,通过计算强度高于应力的概率,就得到零件的可靠度。
根据这一思想建立的可靠度计算模型成为应力-强度干涉模型,这也是进行各种机械零件的概率设计的基础。
狭义的概念的应力-强度干涉模型是以零件的强度指标(例如零件的极限应力lim δ)和作用力σ都是随机变量的客观事实为基础的。
由于它们都是随机变量,因而必然会有相应的分布规律。
令g (r)表示强度指标r 的概率密度函数,p (s )表示作用应力s 的概率密度函数。
显然,零件失效的条件可以用以下两式的任一个来描述r s <0z r s =-<式中,z 可理解为安全裕度。

应力—强度干涉模型在产品可靠性分析中的应用作者:高洋牛耕来源:《科学与财富》2017年第24期摘要:根据机械零部件设计的目标是危险断面上的最小强度不低于最大应力的特点,建立应力—强度干涉模型对机械产品的可靠性进行预计。
以某产品卡紧机构为例,在其应力和强度均服从正态分布的情况下对可靠性进行了预计,为可靠性预计在工程上的应用提供了手段。
关键词:可靠性预计;应力—强度干涉理论;正态分布产品可靠性预计是根据组成产品的元件、部件及分组件的可靠性推测产品的可靠性,进行可靠性预计时应考虑到产品各组成部分的使用条件及环境、功能要求、设计水平、工艺条件等因素。
通过可靠性预计结果与该产品要求的可靠性指标进行比较,审查是否达到产品设计任务中提出的可靠性指标和分配给各设备的可靠性指标,另外通过可靠性预计可以发现设计中的薄弱环节,并采取相应的措施加以改进,以提高产品的可靠性水平,同时可以为可靠性试验方案的选取提供依据。
因此在产品方案研究和工程研制阶段,应及时地预计、分析系统或设备的可靠性,以利于比较不同设计方案的特点及可靠度,选择最佳设计方案,并实施“预计—改进设计”的循环,使产品达到规定的可靠性要求。
目前可靠性预计常见的方法有全概率法、相似产品预计法、数学模型法、故障率预计法等。
这些方法往往精度不高,带有局限性。
应力—强度干涉方法不仅综合考虑了应力和强度的均值及它们的变异性对可靠度的影响,而且还考虑了基本变量的概率分布类型,从而可以较全面地反映各种不确定因素的影响,提供较多的设计信息,实现将可靠度直接引入到零件的设计中,定量回答零件在运动中的安全与可靠的程度。
1 应力—强度干涉模型机械零部件设计的基本目标是,在一定的可靠度下保证其危险断面上的最小强度(抗力)不低于最大的应力,否则,零件将由于未满足可靠度要求而导致失效。
这里的应力和强度都不是一个确定的值,而是由若干随机变量组成的多元随机函数,它们具有一定的分布规律,随着时间的推移,由于环境、使用条件等因素的影响,材料强度退化,导致在某个时间应力与强度分布发生干涉(图中阴影部分),这时零部件可能发生失效。
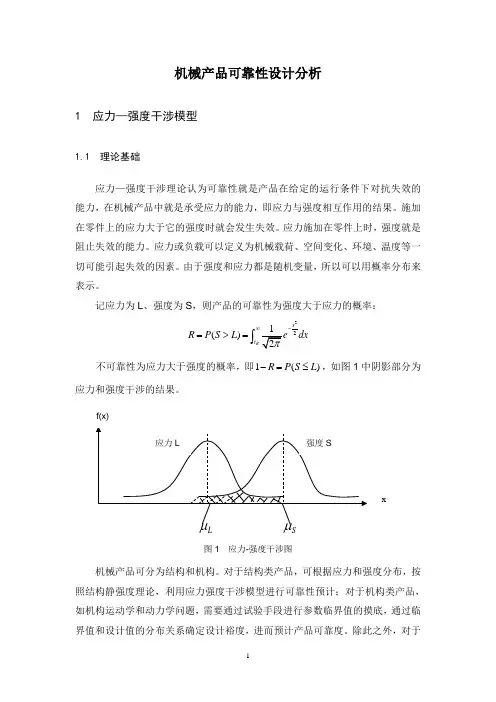
机械产品可靠性设计分析1 应力—强度干涉模型1.1 理论基础应力—强度干涉理论认为可靠性就是产品在给定的运行条件下对抗失效的能力,在机械产品中就是承受应力的能力,即应力与强度相互作用的结果。
施加在零件上的应力大于它的强度时就会发生失效。
应力施加在零件上时,强度就是阻止失效的能力。
应力或负载可以定义为机械载荷、空间变化、环境、温度等一切可能引起失效的因素。
由于强度和应力都是随机变量,所以可以用概率分布来表示。
记应力为L、强度为S,则产品的可靠性为强度大于应力的概率:22()RxtR P S L dx∞-=>=⎰不可靠性为应力大于强度的概率,即1()R P S L-=≤,如图1中阴影部分为应力和强度干涉的结果。
图1 应力-强度干涉图机械产品可分为结构和机构。
对于结构类产品,可根据应力和强度分布,按照结构静强度理论,利用应力强度干涉模型进行可靠性预计;对于机构类产品,如机构运动学和动力学问题,需要通过试验手段进行参数临界值的摸底,通过临界值和设计值的分布关系确定设计裕度,进而预计产品可靠度。
除此之外,对于机械产品还存在疲劳等可靠性问题,都可以利用概率设计方法,利用机械可靠性设计的思想来进行可靠性计算。
1.2 正态分布可靠度计算方法在不很精确的概率设计法可靠性计算中,通常不考虑随机变量的实际分布而假定服从正态分布或对数正态分布,利用正态分布进行可靠度计算。
在假设应力、强度均为正态分布随机变量2(,)L LN μσ、2(,)s s N μσ且相互独立情况下,可靠性表示为:()R R t =ΦR t =或R t =式中,S μ——强度均值;L μ——应力均值; S σ——强度标准差; L σ——应力标准差;SL f μμ=; SS S C σμ=; LL LC σμ=; 当应力为一确定的量L 时,()S SLR μσ-=Φ 如果应力和强度的母体分布参数均值和方差未知时,用样本均值和样本方差来代替。
产品强度试验结果取得x n 个强度试验值1x ,2x ,…,x n x ;产品应力试验结果取得y n 个应力试验值1y ,2y ,…,y n y 。


应力强度干涉模型
应力强度干涉模型是法律领域重要且广泛应用的模型之一。
在恩格斯-科尔杨宪法构想中,宪法是政治体系中最高子系统,且史无前例,它有自己特殊的内涵,这一内涵可以采用应力强度干涉模型来表述,因为它保证不受任何组织和政治实体的行为支配。
应力强度干涉模型,称作应力强度模型,是一种理论模型,可以应用于提供合理的预测与建议。
这一模型将政府决策的实施后果,以及政府和市民在社会中的作用推敲起来,做出相应的应力,备受宪法的约束,并以不受宪法的支配的情况下进行行动。
应力强度干涉模型,以最小损耗的前提下,及双方同意的前提下,达成最为可行的效果。
它让双方各自坚持自己的利益,宪法与其他法律可以得到更好而更快的执行,解决双方冲突的效果也将更加明显,而非有害于宪法和法律维护权利和自由的双方分歧。
应力强度干涉模型还具有灵活性,可以在繁多的政治,经济,文化,社会等社会文化情况下保持有效的。
相应的,即便是在变动的环境中,它仍然能够维护宪法尊崇的目标。
综上所述,应力强度干涉模型是宪法研究中重要的模型。
它不仅有利于促进政治,经济风险的平衡,而且可以有效地维护法律权利和自由,帮助政府更有效地推进社会建设,从而实现法治。