应力—强度干涉模型在产品可靠性分析中的应用
- 格式:doc
- 大小:868.00 KB
- 文档页数:7


交流接触器中分磁环的可靠性分析摘要:本文利用Maxwell 3D软件和ePhysics分析软件对交流接触器的电磁机构的稳态特性进行分析。
以CJ20-25型交流接触器的电磁机构为例,仿真分析了分磁环的最大应力,对分磁环进行了可靠性分析。
关键词:交流接触器分磁环ANSOFT 应力可靠性分析可靠性技术是20世纪50年代发展起来的一门技术,它包括可靠性设计、可靠性制造、可靠性管理、可靠性试验及失效分析等内容。
一个控制系统或电力系统的可靠性在很大程度取决于该系统中所用元件或设备的可靠性,如果元件或设备的可靠性不高,则系统的可靠性就很难得到保证。
在很多系统中,电磁电器占很大比例,而电磁电器的感测机构大都是电磁系统,电磁系统是各种电磁电器的重要组成部分,因而电磁系统的可靠性研究十分重要。
在交流接触器电磁机构中,因为分磁环受到洛仑兹力,会产生形变,如果分磁环的设计不合理,或者分磁环的材料不合理,会导致分磁环的松动或断裂,从而导致电磁机构所受到的最小电磁吸力不能满足要求,不能消除接触器的振动与噪声。
本文利用Ansoft公司开发的Maxwell 3D软件对交流接触器的电磁机构的稳态特性进行分析与仿真,并用ePhysics软件对交流接触器电磁机构分磁环进行应力计算。
基于应力-强度干涉模型对分磁环进行了可靠性分析。
1 交流接触器电磁机构分析模型CJ20-25型交流接触器的双E型电磁机构的模型如图1所示。
利用Maxwell 3D软件对其实体进行建模,几何模型包括:动铁心、静铁心、线圈、分磁环和求解区域。
对于已经建立好的交流电磁机构来说,我们设置求解区域为空气;输入B-H曲线定义静铁心和动铁心的材料;设置线圈和分磁环的材料为铜。
建完几何模型后,为各实体赋予已定义好的材料属性,随后即可以进行网格剖分。
本文对动静铁心、线圈进行的网格划分,是采用的手动网格剖分。
定义上下铁心剖分的网格最大边长为5mm,线圈剖分的网格最大边长为4mm,分磁环剖分的最大边长为0.4mm。

产品可靠性研究与方法产品、系统在规定的条件下,规定的时间内,完成规定功能的能力称为可靠性.可靠性的评价可以使用概率指标或时间指标,这些指标有:可靠度、失效率、平均无故障工作时间、平均失效前时间、有效度等.典型的失效率曲线是澡盆曲线,其分为三个阶段:早期失效区、偶然失效区、耗损失效区。
早期失效区的失效率为递减形式,即新产品失效率很高,但经过磨合期,失效率会迅速下降。
偶然失效区的失效率为一个平稳值,意味着产品进入了一个稳定的使用期。
耗损失效区的失效率为递增形式,即产品进入老年期,失效率呈递增状态,产品需要更新.提高可靠性的措施可以是:对元器件进行筛选;对元器件降额使用,使用容错法设计(使用冗余技术),使用故障诊断技术等。
产品可靠性可靠性(dependability;reliability;security)可靠性的定义根据国家标准GB-6583的规定,产品的可靠性是指:产品在规定的条件下、在规定的时间内完成规定的功能的能力。
一般所说的“可靠性”指的是“可信赖的"或“可信任的"。
我们说一个人是可靠的,就是说这个人是说得到做得到的人,而一个不可靠的人是一个不一定能说得到做得到的人,是否能做到要取决于这个人的意志、才能和机会。
同样,一台仪器设备,当人们要求它工作时,它就能工作,则说它是可靠的;而当人们要求它工作时,它有时工作,有时不工作,则称它是不可靠的。
对产品而言,可靠性越高就越好。
可靠性高的产品,可以长时间正常工作(这正是所有消费者需要得到的);从专业术语上来说,就是产品的可靠性越高,产品可以无故障工作的时间就越长。
简单的说,狭义的“可靠性”是产品在使用期间没有发生故障的性质。
例如一次性注射器,在使用的时间内没有发生故障,就认为是可靠的;再如某些一旦发生故障就不能再次使用的产品,日光灯管就是这类型的产品,一般损坏了只能更换新的。
从广义上讲,“可靠性”是指使用者对产品的满意程度或对企业的信赖程度。



机械设计中的可靠性分析在现代工业生产中,机械设计是一个至关重要的环节。
而可靠性作为衡量机械产品质量的关键指标之一,对于确保机械系统的稳定运行、提高生产效率、降低维护成本以及保障人员安全都具有极其重要的意义。
可靠性指的是产品在规定的条件下和规定的时间内,完成规定功能的能力。
在机械设计中,可靠性分析旨在预测和评估机械产品在其整个生命周期内可能出现的故障和失效模式,进而采取相应的措施来提高产品的可靠性。
机械产品的可靠性受到多种因素的影响。
首先,设计阶段的参数选择和结构设计直接关系到产品的可靠性。
例如,不合理的零部件尺寸、形状以及材料选择,可能导致零件在工作过程中过早失效。
其次,制造工艺的精度和质量控制对可靠性也有显著影响。
制造过程中的误差、缺陷以及热处理不当等问题,都可能削弱产品的性能和可靠性。
再者,使用环境的复杂性和恶劣程度也是不可忽视的因素。
高温、高湿、腐蚀、振动等恶劣环境条件会加速机械零件的磨损和老化,从而降低产品的可靠性。
此外,维护保养的及时性和有效性对于延长机械产品的使用寿命和保持其可靠性同样至关重要。
为了进行有效的可靠性分析,工程师们通常采用多种方法和技术。
故障模式与影响分析(FMEA)是一种常见的方法,它通过对系统中各个潜在的故障模式进行识别、分析其可能产生的影响,并评估其严重程度、发生概率和检测难度,从而为设计改进提供依据。
另一种常用的方法是故障树分析(FTA),它以系统的故障为顶事件,通过逻辑推理逐步找出导致故障发生的各种原因组合,有助于深入了解系统的故障机理和制定针对性的预防措施。
可靠性试验也是可靠性分析的重要手段之一。
通过对机械产品进行模拟实际工作条件的试验,可以直接观察和记录产品的性能变化和故障情况,为可靠性评估提供真实可靠的数据。
此外,基于概率统计的可靠性计算方法,如应力强度干涉模型,可以定量地评估机械零件在给定工作条件下的可靠度。
在机械设计过程中,提高可靠性的措施多种多样。




基于载荷-强度干涉模型的零件可靠性分析高鹏;谢里阳【摘要】分析了随机载荷大小对强度退化的影响,提出考虑强度退化和载荷作用次数的可靠度计算模型.该模型通过计算当量载荷,将随机栽荷作用下的强度退化过程等效为确定性载荷作用下的退化过程,得到零件可靠度与载荷作用次数的关系,在此基础上,通过分析不同载荷出现次数与时间的关系,得到多个载荷共同作用下零件可靠度随时间的变化规律.【期刊名称】《中国机械工程》【年(卷),期】2010(021)006【总页数】5页(P698-702)【关键词】可靠性;载荷;载荷强度干涉;泊松过程【作者】高鹏;谢里阳【作者单位】东北大学,沈阳,110004;东北大学,沈阳,110004【正文语种】中文【中图分类】TH122;TB114.30 引言可靠性是贯穿于产品全生命周期内用以衡量产品质量的重要指标,包含于产品的规划、设计、制造、试验、管理以及维修的各个环节中。
零件作为机械产品的重要组成部分,其可靠性的正确评估对于产品的安全运行具有重大的实际意义。
载荷-强度干涉模型是分析机械零部件可靠性的重要手段。
在载荷和强度已知的条件下,可以利用载荷-强度干涉模型通过积分来计算零件强度大于载荷的概率。
但是传统的载荷-强度干涉模型往往只考虑载荷作用一次时零件的可靠度,忽略了载荷作用次数对可靠度计算的影响[1-5]。
文献[6]分析了考虑载荷作用次数的零件可靠度分析方法,较好地分析了载荷作用次数对零件和系统可靠性的影响,但建立的模型实际上将强度看作随机变量,认为载荷作用过程中强度不退化。
文献[7]分析了零件强度的退化规律。
文献[8]将载荷和强度这两个因素相结合,考虑了强度随载荷作用次数的退化规律,更加符合零部件的实际工作状态,但所建立的模型没有考虑载荷的随机性及其对强度退化过程的影响,不能用于随机载荷下的零件可靠度分析。
此外,上述文献中提出的模型只适用于零件承受一种载荷的分析,且没有考虑载荷出现次数的随机性。
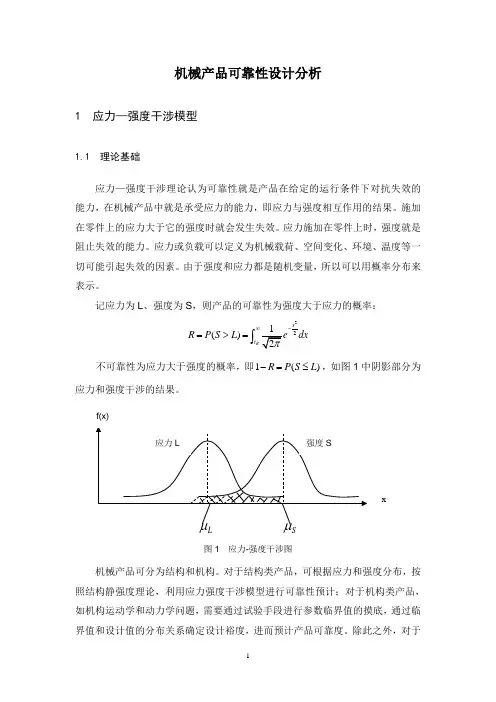
机械产品可靠性设计分析1 应力—强度干涉模型1.1 理论基础应力—强度干涉理论认为可靠性就是产品在给定的运行条件下对抗失效的能力,在机械产品中就是承受应力的能力,即应力与强度相互作用的结果。
施加在零件上的应力大于它的强度时就会发生失效。
应力施加在零件上时,强度就是阻止失效的能力。
应力或负载可以定义为机械载荷、空间变化、环境、温度等一切可能引起失效的因素。
由于强度和应力都是随机变量,所以可以用概率分布来表示。
记应力为L、强度为S,则产品的可靠性为强度大于应力的概率:22()RxtR P S L dx∞-=>=⎰不可靠性为应力大于强度的概率,即1()R P S L-=≤,如图1中阴影部分为应力和强度干涉的结果。
图1 应力-强度干涉图机械产品可分为结构和机构。
对于结构类产品,可根据应力和强度分布,按照结构静强度理论,利用应力强度干涉模型进行可靠性预计;对于机构类产品,如机构运动学和动力学问题,需要通过试验手段进行参数临界值的摸底,通过临界值和设计值的分布关系确定设计裕度,进而预计产品可靠度。
除此之外,对于机械产品还存在疲劳等可靠性问题,都可以利用概率设计方法,利用机械可靠性设计的思想来进行可靠性计算。
1.2 正态分布可靠度计算方法在不很精确的概率设计法可靠性计算中,通常不考虑随机变量的实际分布而假定服从正态分布或对数正态分布,利用正态分布进行可靠度计算。
在假设应力、强度均为正态分布随机变量2(,)L LN μσ、2(,)s s N μσ且相互独立情况下,可靠性表示为:()R R t =ΦR t =或R t =式中,S μ——强度均值;L μ——应力均值; S σ——强度标准差; L σ——应力标准差;SL f μμ=; SS S C σμ=; LL LC σμ=; 当应力为一确定的量L 时,()S SLR μσ-=Φ 如果应力和强度的母体分布参数均值和方差未知时,用样本均值和样本方差来代替。
产品强度试验结果取得x n 个强度试验值1x ,2x ,…,x n x ;产品应力试验结果取得y n 个应力试验值1y ,2y ,…,y n y 。
文章编号:1673 5196(2020)06 0168 05应力 强度干涉理论在对接焊缝中的应用韦尧兵,张如鹏,刘俭辉,王有良(兰州理工大学机电工程学院,甘肃兰州 730050)摘要:针对钢桥承载能力是否满足实际需求的问题,提出了一种将应力 强度干涉理论应用于钢桥对接焊缝数值分析的方法.对钢桥整体结构进行静力学分析,得到了钢桥主梁不同位置的应力状态;通过应力 强度干涉理论分析静载条件下对接焊缝的可靠性;以Q345钢对接焊缝为例,验证了提出方法的可行性,分析了含有残余应力的对接焊缝的可靠性.分析结果表明,在钢桥焊缝没有消除残余应力时,焊缝可靠性显著降低.关键词:对接焊缝;残余应力;数值分析;可靠性中图分类号:O346 文献标志码:A犃狆狆犾犻犮犪狋犻狅狀狅犳狊狋狉犲狊狊 狊狋狉犲狀犵狋犺犻狀狋犲狉犳犲狉犲狀犮犲狋犺犲狅狉狔犻狀犫狌狋狋狑犲犾犱狊WEIYao bing,ZHANGRu peng,LIUJian hui,WANGYou liang(CollegeofMechano ElectronicEngineering,LanzhouUniv.ofTech.,Lanzhou 730050,China)犃犫狊狋狉犪犮狋:Inordertosolvetheproblemofwhetherthebearingcapacityofsteelbridgemeetstheactualdemand,amethodofapplyingstress strengthinterferencetheorytothenumericalanalysisofbuttweldofsteelbridgeisproposedinthispaper.Firstofall,throughstaticanalysisofwholestructureofthesteelbridge,thestressstatesatdifferentpositionsofmaingirderofthesteelbridgecanbeobtained.Secondly,thereliabilityofbuttweldunderstaticloadingisanalyzedbythestress strengthinterferencetheory.Fi nally,takingthebuttweldingofQ345steelasanexample,thefeasibilityoftheproposedmethodisveri fied.Thereliabilityofthebuttweldwithresidualstressispredictednumericallyaswell.犓犲狔狑狅狉犱狊:buttweld;residualstress;numericalanalysis;reliability 随着高速公路里程数的不断增加,高速路桥数量也在不断增加,但高速路桥在建造和使用过程中出现的问题严重影响了高速路桥的使用寿命,甚至威胁到人身和财产安全,所以桥梁建造的可靠性受到人们的广泛关注.王松根等[1]、吴光宇等[2]认为桥梁的实际承载能力与设计承载能力是不同的,提出了考虑结构双重非线性的大跨预应力混凝土桥梁极限承载力分析方法,并计算了混凝土桥梁极限承载力.张劲泉等[3]指出我国公路桥梁承载能力检测评定规程没有明确其目标可靠度,尚属于半经验性半可靠性的评定规程,通过分析明确了现评定规程的研究方向,校准了现评定规程隐含的可靠度指标,给出了计算桥梁历史失效概率的方法,得到了确定评 收稿日期:2019 09 02 基金项目:国家自然科学基金青年基金(51605212),甘肃省自然科学基金(17JR5RA122) 作者简介:韦尧兵(1965 ),男,甘肃靖远人,教授.定规范目标可靠度的主要依据,为我国公路桥梁承载能力评定规程的进一步完善提供了建议.Shan等[4]通过实验和非线性数值计算研究了钢 聚氨酯夹层桥面板的屈曲,结果表明,当夹层桥面板受压时,越靠近中间部分,钢板的纵向压应力越大,但加强筋底部的纵向压应力越小.Lee等[5]介绍了在基于可靠性的设计规范中,目标可靠性指标和相应风荷载系数的一般程序;进行蒙特卡罗模拟以揭示风速和压力的统计参数之间的关系.提出了一种基于极限状态下风速返回周期确定目标可靠性指标的方法,该方法用于计算韩国公路桥梁设计规范中电缆支撑桥梁的目标可靠性指标.吴光宇等[2]、张劲泉等[3]从桥梁整体结构的角度来考虑桥梁的可靠性,为我国的桥梁事业做出了巨大的贡献,为桥梁建设者提供了大量宝贵的经验,但是钢桥局部可靠性对整体寿命的影响不能够被忽略.焊接是现代钢结构最主要的连接方式之一[6].相第46卷第6期2020年12月兰 州 理 工 大 学 学 报JournalofLanzhouUniversityofTechnologyVol.46No.6Dec.2020较于螺栓连接和铆钉连接,具有结构简单,强度高、气密性好,生产效率高的优点[7].但是由于不均匀的局部加热,焊接完成后会产生残余应力[8].葛明兰等[9]分别从焊接残余应力对结构的刚度、受压杆件稳定性、静载强度、疲劳强度、构件脆性、焊件加工精度和尺寸稳定性等方面研究残余应力对焊接结构产生的影响.高耀东等[10]利用ANSYS软件对焊接过程进行有限元模拟,获得了焊接温度场及残余应力场的分布规律.梁晓燕等[11]比较了基于ANSYS平台的焊接温度场模拟过程中不同热源模式对计算结果的影响.Wang等[12]和Balakrishnan等[13]分别从焊接速度,焊接方法对焊接残余应力进行了研究.李斌等[14]对钢结构焊接所使用的热应力法进行了详细的研究.残余应力的存在会导致局部可靠性下降,从而影响钢桥整体的承载能力和使用寿命,所以针对钢桥焊缝的可靠性研究显得尤为重要.1 应力强度干涉理论可靠性设计是现代设计理论的一种设计方法[15].机械强度的可靠性设计是将概率统计的基本理论应用到机械工程设计中的一种新方法[16].以应力强度分布的干涉理论为基础的可靠性设计,在满足可靠性设计的前提下,提高了经济效益.与传统静强度设计方法相比,应力 强度分布的干涉理论把应力狊和强度犮设定为服从某种分布函数的随机变量,犵(狊)和犳(犮)分别表示应力和强度的概率密度函数(图1).一个零件是否可靠,就以强度犮大于应力狊的概率大小来判定,即当强度犮小于工作应力狊时发生失效.图1 应力 强度干涉图犉犻犵.1 犛狋狉犲狊狊 狊狋狉犲狀犵狋犺犻狀狋犲狉犳犲狉狅犵狉犪犿在实际工程中应力狊和强度犮服从正态分布,即犆~犖(μ犮,σ犮),犛~犖(μ狊,σ狊)犆犚=μ犆+狕犆σ犆, 犛犚=μ犛+狕犛σ犛(1)式中:犆犚、犛犚分别为可靠度犚对应的材料强度和结构应力;μ犆、μ犛分别为强度和应力的均值;σ犮、σ狊分别为强度和应力的标准差;狕犆=Φ-1(1-犚);狕犛=Φ-1(犚).由此,可以得出不同可靠度下的安全系数:狀犚=犆犚犛犚=μ犮+狕犮σ犮μ犛+狕犛σ犛(2) 该方法简单有效地建立了可靠性与应力强度之间的关系,无需考虑材料、尺寸对构建可靠性的影响,具有广泛的适用性.焊缝可靠性的问题即焊接质量的问题,焊接质量通常由设计质量、加工质量、质量检验和焊后处理等环节来保证,其中设计质量决定了焊接质量.焊接产品所选用的接头类型及其计算强度应满足实际的承载能力.为了满足焊接设计质量,本文将应力 强度干涉理论应用于高速路桥焊缝可靠性分析.2 算例某高速路钢桥主体模型如图2所示,设计使用年限100年.桥梁构件钢材为Q345钢,构件厚度为10~40mm,钢桥采用焊接方式连接,焊缝质量等级为一级的对接焊缝,抗拉强度为270MPa[17].图2 钢桥主体模型图犉犻犵.2 犛狋犲犲犾犫狉犻犱犵犲犫狅犱狔犿狅犱犲犾犱犻犪犵狉犪犿钢桥桥面尺寸为51m×15m,钢桥体积为49.953m3,混凝土体积为23.175m3,沥青体积为30.9m3.将应力强度干涉理论应用于高速路桥焊缝可靠性的计算,在计算可靠度安全系数时,应充分考虑应力的分散性,根据相关设计规范[18],取材料静强度变异系数为0.07.因此,式(2)可以转化为式(3):狀犚=犆犚犛犚=(1+狕犮犆犮)μ犆μ犛(3)式中:狀犚为不同可靠度下的安全系数;犆犮为材料静强度变异系数.依照国家标准对钢桥进行极限状态静力学分析[19],对持久设计状况和短暂设计状况应采用作用的基本组合,作用基本组合的效应值按式(4)计算:犛ud=γ0犛(∑犿犻=1G犻d,Q1d,∑狀犼=2Q犼d)(4)·961·第6期 韦尧兵等:应力强度干涉理论在对接焊缝中的应用 式中:犛ud为承载能力极限状态下作用基本组合的效应设计值;γ0为结构重要性系数,钢桥设计安全等级为一级,结构重要性系数取1.1;G犻d为第犻个永久作用的设计值;Q1d为汽车荷载的设计值;Q犼d为除汽车荷载外其他第犼个可变作用的设计值.实际工程中桥面作用类型见表1所列.表1 桥面载荷犜犪犫.1 犜犪犫犾犲狅犳犾狅犪犱狊犻狀犫狉犻犱犵犲犱犲犮犽作用类型名称数值/kN永久作用钢桥重力3923.0混凝土重力579.3可变作用沥青重力679.8车道荷载1407.0因钢桥实际尺寸过大,且属于对称结构,为了节省计算时间,采用四分之一建模,单元类型选用Sol id187单元,网格采用自由尺寸划分,如图3所示.图3 钢桥网格划分图犉犻犵.3 犕犲狊犺犳狅狉狊狋犲犲犾犫狉犻犱犵犲对钢桥约束端施加面约束,钢桥作用大小等效为均布载荷,大小为9515Pa,施加在桥面上.求解完成后,进入通用后处理器查看钢桥等效应力分布状态,结果如图4所示.应力最大点出现在钢桥底部应力集中处,大小为108MPa.对钢桥外侧主梁下部定义路径,等间距提取应力值大小,结果见表2所列.图4 钢桥应力图犉犻犵.4 犛狋犲犲犾犫狉犻犱犵犲狊狋狉犲狊狊犿犪狆表2 外侧主梁应力犜犪犫.2 犜犪犫犾犲狅犳狊狋狉犲狊狊犻狀狅狌狋狊犻犱犲犿犪犻狀犫犲犪犿距离/m应力值/MPa083.5551.2588.8482.5088.9653.7588.5805.0081.3696.2585.4537.5082.666由表2可以得出,从钢桥中部向约束端,应力值先增大,然后逐渐减小,符合实际情况.3 残余应力分析选用Q345钢作为焊接母材,其不同温度下力学性能参数见表3所列.钢板尺寸为100mm×50mm×10mm,单边开V形坡口,坡口角度为60°,如图5所示.单元选用Solid70,为三维八节点实体热单元,具备三维热传导能力,可用于三维稳态或瞬态热分析,同时可应用“生死单元”技术.利用APDL语句中的mptemp和mpdata命令建立材料随温度变化的参数库.表3 犙345钢力学性能参数犜犪犫.3 犕犲犮犺犪狀犻犮犪犾狆狉狅狆犲狉狋狔狆犪狉犪犿犲狋犲狉狊狅犳犙345狊狋犲犲犾温度/℃弹性模量/GPa热膨胀系数/(×10-6℃)屈服应力/MPa切变模量/GPa热传导系数比热密度泊松比2021014.83102.0516.348078000.2710020114.8260216.348578000.2850017514.82031.716.349878000.2880010114.870116.350678000.2910006.514.880.00116.352678000.291500114.810.00116.353978000.32·071· 兰州理工大学学报 第46卷图5 焊接接头示意图犉犻犵.5 犛犮犺犲犿犪狋犻犮犱犻犪犵狉犪犿狅犳狋犺犲狑犲犾犱犲犱犼狅犻狀狋设定上下边约束条件,将热分析后的节点温度文件 .rth用ldread命令读入,循环导入各时间步温度,完成求解计算.进入后处理查看结果,求解完成后的残余应力分布状态如图6所示.图6 残余应力分布图犉犻犵.6 犚犲狊犻犱狌犪犾狊狋狉犲狊狊犱犻狊狋狉犻犫狌狋犻狅狀犿犪狆从图6可以看出,残余应力最大位置出现在熔和区附近,随着离焊缝的距离增加,残余应力逐渐减小,直至为0.4 结果分析将不同位置应力值代入式(3)中计算得到无残余应力状态下不同可靠度的安全系数,见表4所列.表4 无残余应力状态下不同可靠度的安全系数犜犪犫.4 犛犪犳犲狋狔犳犪犮狋狅狉狊狅犳犱犻犳犳犲狉犲狀狋狉犲犾犻犪犫犻犾犻狋狔狌狀犱犲狉狀狅狉犲狊犻犱狌犪犾狊狋狉犲狊狊狊狋犪狋犲位置编号当量应力最大值/MPa可靠度安全系数犚=50%犚=95%犚=99%183.553.383.3493.345288.843.1863.1493.146388.963.1813.1453.142481.363.4793.4393.435582.663.4243.3853.381 根据平板对接焊缝残余应力分布,焊接热影响区残余拉应力值为180MPa,分析含有残余拉应力的对接焊缝不同可靠度下的安全系数,见表5所列.表5 含有残余应力状态下不同可靠度的安全系数犜犪犫.5 犆狅狀狋犪犻狀狊狊犪犳犲狋狔犳犪犮狋狅狉狊狅犳犱犻犳犳犲狉犲狀狋狉犲犾犻犪犫犻犾犻狋狔狌狀犱犲狉狉犲狊犻犱狌犪犾狊狋狉犲狊狊狊狋犪狋犲位置编号当量应力最大值/MPa可靠度安全系数犚=50%犚=95%犚=99%183.551.071.061.06288.841.051.041.03388.961.051.041.03481.361.081.071.06582.661.071.061.06 考虑到残余应力会发生松弛现象[20],平板对接焊缝发生应力松弛后的残余拉应力值为110MPa,此时,对接焊缝不同可靠度下的安全系数见表6所列.表6 残余应力松弛状态下不同可靠度的安全系数犜犪犫.6 犛犪犳犲狋狔犳犪犮狋狅狉狊狅犳犱犻犳犳犲狉犲狀狋狉犲犾犻犪犫犻犾犻狋狔狌狀犱犲狉狋犺犲狊狋犪狋犲狅犳狉犲狊犻犱狌犪犾狊狋狉犲狊狊狉犲犾犪狓犪狋犻狅狀位置编号当量应力最大值/MPa可靠度安全系数犚=50%犚=95%犚=99%183.551.451.441.44288.841.411.401.40388.961.411.401.40481.361.471.461.46582.661.461.451.45通过分析表5和表6可以得出以下结论:同种状态下,可靠度越高安全系数越低;不同种状态下,同一可靠度安全系数不同,无残余应力状态下最高,有残余应力状态下最低.5 结论1)通过数值计算的方法,得到了某高速路桥工作时静载条件下的应力状态,结果表明,钢桥次外侧主梁受力最大,但满足实际需求.2)分析了钢桥平板对接焊缝在三种状态下(有/无残余应力和残余应力松弛)不同可靠度的安全系数,分析结果表明,存在残余应力时,钢桥平板对接焊缝可靠性显著降低.3)将应力 强度干涉理论应用于静载条件下的对接焊缝可靠性分析,能够满足工程需要,该方法具有普遍适用性.参考文献:[1] 王松根,李松辉.公路桥梁限载标准的可靠性分析方法[J].工·171·第6期 韦尧兵等:应力强度干涉理论在对接焊缝中的应用 程力学,2010,27(10):162 166+181.[2] 吴光宇,杨升善,汪劲丰,等.大跨预应力混凝土桥梁极限承载力计算[J].南昌大学学报(理科版),2013,37(2):198 204.[3] 张劲泉,冷艳玲,李万恒,等.中国公路桥梁承载能力评定规程的可靠性水准[J].公路交通科技,2015,32(4):59 63+77.[4] SHANC,YIY.Anexperimentalandnumericalstudyonthebehaviorofacontinuousorthotropicbridgedeckwithsandwichconstruction[J].Thin WalledStructures,2017,111:138 144.[5] LEEHS,KIMJH.Windpressurestatisticsandtargetrelia bilityindexforwindload governedlimitstateofreliability basedbridgedesigncodes[J].KSCEJournalofCivilEngineer ing,2019,23(5):2263 2271.[6] 冯艳辉.基于ANSYS的焊接梁残余应力分析[D].西安:西安建筑科技大学,2008:12 13.[7] 张文钺.焊接冶金学[M].北京:机械工业出版社,2004.[8] 侯 彬.钢结构焊接残余应力及焊接变形控制技术分析[J].中国金属通报,2019(2):139 140.[9] 葛明兰,鲁家晟.焊接残余应力对焊接结构的影响[J].福建建筑,2010(7):50 52.[10] 高耀东,何 雪.基于ANSYS单元生死技术的焊接模拟[J].热加工工艺,2010,39(7):120 122+126.[11] 梁晓燕,罗金华,杜汉斌,等.基于ANSYS平台焊接模拟中不同焊接热源的比较[J].电焊机,2003(3):29 32.[12] WANGT,LIN,ZHANGY,犲狋犪犾.Influenceofweldingspeedonmicrostructuresandmechanicalpropertiesofvacuumelec tronbeamweldedTZMalloyjoints[J].Vacuum,2018,149:29 35.[13] BALAKRISHNANJ,VASILEIOUAN,FRANCISJA,犲狋犪犾.Residualstressdistributionsinarc,laserandelectronbeamweldsin30mmthickSA508steel:Across processcomparison[J].InternationalJournalofPressureVesselsandPiping,2018,162:59 70.[14] 李 斌,苗 青,胡志明,等.热应力法在钢结构焊接疲劳模拟中的应用[J].中国建材科技,2020,29(1):92 93.[15] 张 鄂,买买提明·艾尼.现代设计理论与方法[M].北京:科学出版社,2007:109 111.[16] 崔秀林.机械可靠性设计应力与强度干涉理论的应用[J].机械设计,1998(3):33 34+51.[17] 中交公路规划设计院有限公司.公路钢结构桥梁设计规范:JTGD64—2015[S].北京:人民交通出版社,2015.[18] 中华人民共和国住房和城乡建设部.钢结构设计标准:GB50017—2017[S].北京:中国建筑工业出版社,2017.[19] 牟致忠.机械可靠性:理论·方法·应用[M].北京:机构工业出版社,2011:85.[20] 王成刚,何 凡.异种钢焊接接头的焊接残余应力及其松弛行为[J].焊接技术,2016,45(4):66 69+6.·271· 兰州理工大学学报 第46卷。
应力-强度干涉模型下的滚动轴承可靠性评估与设计方法李燕科;邱明;李军星;牛凯岑;许艳雷
【期刊名称】《机械科学与技术》
【年(卷),期】2024(43)3
【摘要】针对滚动轴承可靠性低、缺乏设计依据等问题,提出一种应力-强度干涉模型下的滚动轴承可靠性评估与设计方法。
考虑滚动轴承实际承载当量动载荷和规定当量动载荷的随机特性,假设两者为服从对数正态分布的随机变量,建立滚动轴承可靠性评估与设计模型。
其次,对多型号多工况下的深沟球轴承和角接触球轴承进行仿真验证,结果表明:本文提出的滚动轴承可靠性评估与设计方法,通过分析当量动载荷的许用范围,结合轴承设计公式可以使优化后的轴承满足在该工况下的目标可靠性寿命,准确有效的实现滚动轴承的可靠性评估与设计。
【总页数】7页(P416-422)
【作者】李燕科;邱明;李军星;牛凯岑;许艳雷
【作者单位】河南科技大学机电工程学院;河南科技大学机械装备先进制造河南省协同创新中心
【正文语种】中文
【中图分类】TH133.3
【相关文献】
1.应力-强度相关性干涉下的随机安全系数与零件可靠性设计
2.复合应力作用下强度退化的应力-强度干涉模型可靠性统计分析
3.基于应力—强度干涉理论进行一定
置信度下的可靠性设计4.基于应力-强度干涉模型的火工品可靠性设计方法5.基于应力–强度干涉模型的随机应力下变压器故障概率估算方法
因版权原因,仅展示原文概要,查看原文内容请购买。
应力—强度干涉模型在产品可靠性分析中的应用
作者:高洋牛耕
来源:《科学与财富》2017年第24期
摘要:根据机械零部件设计的目标是危险断面上的最小强度不低于最大应力的特点,建立应力—强度干涉模型对机械产品的可靠性进行预计。
以某产品卡紧机构为例,在其应力和强度均服从正态分布的情况下对可靠性进行了预计,为可靠性预计在工程上的应用提供了手段。
关键词:可靠性预计;应力—强度干涉理论;正态分布
产品可靠性预计是根据组成产品的元件、部件及分组件的可靠性推测产品的可靠性,进行可靠性预计时应考虑到产品各组成部分的使用条件及环境、功能要求、设计水平、工艺条件等因素。
通过可靠性预计结果与该产品要求的可靠性指标进行比较,审查是否达到产品设计任务中提出的可靠性指标和分配给各设备的可靠性指标,另外通过可靠性预计可以发现设计中的薄弱环节,并采取相应的措施加以改进,以提高产品的可靠性水平,同时可以为可靠性试验方案的选取提供依据。
因此在产品方案研究和工程研制阶段,应及时地预计、分析系统或设备的可靠性,以利于比较不同设计方案的特点及可靠度,选择最佳设计方案,并实施“预计—改进设计”的循环,使产品达到规定的可靠性要求。
目前可靠性预计常见的方法有全概率法、相似产品预计法、数学模型法、故障率预计法等。
这些方法往往精度不高,带有局限性。
应力—强度干涉方法不仅综合考虑了应力和强度的均值及它们的变异性对可靠度的影响,而且还考虑了基本变量的概率分布类型,从而可以较全面地反映各种不确定因素的影响,提供较多的设计信息,实现将可靠度直接引入到零件的设计中,定量回答零件在运动中的安全与可靠的程度。
1 应力—强度干涉模型
机械零部件设计的基本目标是,在一定的可靠度下保证其危险断面上的最小强度(抗力)不低于最大的应力,否则,零件将由于未满足可靠度要求而导致失效。
这里的应力和强度都不是一个确定的值,而是由若干随机变量组成的多元随机函数,它们具有一定的分布规律,随着时间的推移,由于环境、使用条件等因素的影响,材料强度退化,导致在某个时间应力与强度分布发生干涉(图中阴影部分),这时零部件可能发生失效。
通常把这种干涉称为应力—强度干涉模型,如图1所示。
图1 应力—强度干涉模型
可靠性的核心是完成规定的功能,它取决于应力和强度互相干涉的结果。
强度S、应力s 都是随机变量,强度和应力的差Z=S-s,也是随机变量。
它表示了零部件所处的状态,即
Z>0,零件处于安全状态;
Z
Z=0,零件处于极限状态。
2 可靠性预计应力和强度分布的选择及应力—强度干涉模型建立
2.1 应力和强度分布的选择
机械结构所受的载荷一般是随机变量,其分布特性用载荷的概率分布函数来描述。
工程上常用的载荷分布主要包括正态分布、对数正态分布、威布尔(Weibull)分布、冈贝尔(Gumbel)等。
机械结构载荷分为静载荷、动载荷、疲劳载荷和热载荷。
载荷为静载荷时所受载荷的分布、薄弱位置的应力分布以及所用材料的屈服强度分布通常情况下均为正态分布。
应力sfi和强度Sf为正态分布时的概率密度函数为:
2.2 应力—强度干涉模型建立
各组成构件的应力sfi和强度Sf为正态分布时,其干涉变量Zfi=Sf-sfi也服从正态分布,Zfi概率密度函数如下:
各组成构件的可靠度为:
将上式化为标准正态分布,令,则上式可写成:
上式中积分上限βfi称为可靠度系数,它把应力分布参数、强度分布参数及可靠度三者联系起来,是构件可靠性分析的安全指标。
其计算公式如下:
各组成构件的可靠度系数βfi,可由上式计算得出,从标准正态分布表中可查出各构件的可靠度值Rfi。
3 卡紧机构可靠性预计分析与计算
3.1 卡紧机构的可靠性框图
卡紧机构为某发射装置的关键件,用来固定弹体,对弹体的贮存、运输和正常发射起到重要作用。
该机构主要由左右两个卡块和销轴组成,可靠性框如图2所示:
图2 卡紧机构可靠性框图
3.2 可靠性数学模型
设卡紧机构各组件的可靠度和故障率分别为:
(1)卡紧机构:R(λ);
(2)左卡块:R1(λ1);
(3)右卡块:R2(λ2);
(4)销轴:R3(λ3)。
图2可知,卡紧机构在执行任务时,其可靠性数学模型为串联模型,故其可靠性数学模型为:
R=R1R2R3
根据常见的寿命分布类型及适用范围,这里可假设卡紧机构寿命近似服从指数分布,故其可靠性数学模型为:
λ=λ1+λ2+λ3
式中,t为任务时间,可假设t=5h。
3.3 卡紧机构强度计算
卡块材料采用35CrMnSiA高强度合金结构钢,其屈服强度σs=900MPa,销轴材料采用
45#钢,其剪切强度Sτ=450MPa;零件所受载荷的分布、薄弱位置的应力分布以及所用材料的屈服强度分布均为正态分布,运用应力—强度干涉方法计算各构件的可靠度及故障率。
把该卡紧机构卡块和销轴的三维模型输入到ANSYS系统中,约束卡爪臂销轴孔的平移自由度,在单个卡块上接触表面施加载荷F=30000N,卡块的网格划分如图3所示,卡块的应力计算结果见图4所示;销轴起联接机座与卡块的作用,对销轴圆柱段两端及中间区域进行约束,在约束段之间施加同一方向的载荷F=60000N,销轴的网格划分如图5所示,销轴的应力计算结果见图6所示。
图3 卡块网格划分、约束及加载图4 卡块加载后应力分布
图5 销轴网格划分、约束及加载图6 销轴加载后应力分布
从上述的计算结果可以看到,单个卡块在施加载荷后,应力最大值为467MPa,销轴在施加载荷后,应力最大值为349MPa。
3.4 卡紧机构可靠性预计计算
由于卡紧机构各零件所受载荷的分布、薄弱位置的应力分布以及所用材料的屈服强度分布均为正态分布,由上节3.3分析可确定卡紧机构各组件的强度S和应力s正态分布的的均值μS 和μs,通过相关资料的查阅可确定各组件强度S的标准差σS,通过相关资料的查阅以及试验数据的分析可以确定各组件应力s的标准差σS。
卡紧机构各组件的可靠度系数βi,可计算得出。
然后通过标准正态分布表可得出各组件可靠度值Ri,卡紧机构的可靠度R可计算得出,卡紧机构的故障率及各组件的故障率λi可计算得出。
卡紧机构各组件具体计算参数及结果见表1。
表1 卡紧机构各组件的可靠度及故障率计算表
通过运用应力—强度干涉方法计算得出了顶紧机构各组件的可靠度及故障率。
由表1可知,卡紧机构在施加相应载荷的作用下,其可靠度为0.99998,故障率为0.000004。
4 结束语
本文系统阐述了应力—强度干涉的原理,建立了应力和强度均服从正态分布时的可靠度计算模型,通过实例详细介绍了该算法在可靠度预计中的应用。
在今后的产品研发过程中,可以利用应力—强度干涉的方法预计产品的可靠性指标,为提高产品质量以及后续的可靠性工作提供依据和帮助。
■
参考文献
[1] 李良巧,顾唯明.力机械可靠性设计与分析[M].北京:国防工业出版社验,1998:90-103
[2] 李培基.应力分析法可靠性预计实践中的几点认识[J].电子产品可靠性与环境试验,2001,5:19-21
[3] 陈常顺,管红根,高树滋.导弹早期设计阶段火炮的可靠性预测[J].舰火炮发射与控制学报,2000,1:55-58
[4] 王远达,宋笔锋.系统可靠性预计方法综述[J].飞机设计,2008,28(1):37-42
作者简介:高洋(1978—)毕业于西安理工大学,硕士研究生,工程师。
牛耕,(1983—),毕业于北京航空航天大学,硕士研究生,工程师。