异步二进制加法计数器共89页文档
- 格式:ppt
- 大小:11.52 MB
- 文档页数:45



数字电路实验报告
2n进制异步加法计数器
每一级触发器均组成T’触发器,即Qn+l=Qn,故JK触发器J=K=1;D触发器D=Q n 最低位触发器每来一个时钟脉冲翻转一次,低位由l-0时向高位产生进位,高位翻转。
对下降沿触发的触发器,其高位的CP端应与其邻近低位的原码输出Q端相连,即CPm=Qm-1,;对上升沿触发的触发器,其高位的CP端应与其邻近低位的反码输出Q端相连,即CP=Qm-1。
D触发器构成上升沿触发异步3位二进制加法计数器:
电路图:
结果图:
JK下降沿触发异步3位二进制加法计数器:
电路图:
结果图:
2n进制异步减法计数器
每级触发器仍组成T’触发器。
最低位触发器每来一个时钟脉冲翻转一次,低位由1-0时向高位产生借位,高位翻转。
对下降沿触发的触发器,其高位CP端应与其邻近低位的反码端Q相连,即CP=Qm-1,:对上升沿触发的触发器,其高位CP端应与其邻近低位的原码端Q相连,即CPm=Qm-1,。
D上升沿触发异步3位二进制减法计数器:电路图:
结果图:
JK下降沿触发异步3位二进制减法计数器:电路图:
结果图:
实验总结:
通过本次试验已经掌握2n进制异步加法计数器、2n进制异步减法计数器,这次试验学会了很多其次做实验的正确方法是先画好电路图,按图接线,最后检测,后做实验需要小心谨慎,思维敏捷。
不过过程中有些地方没有搞得很懂,还是问了其他同学后,在他的帮助下才做出来的。

二进制计数器计数器是数字系统中用得较多的基本逻辑器件。
它不仅能记录输入时钟脉冲的个数,还可以实现分频、定时、产生节拍脉冲和脉冲序列等。
例如,计算机中的时序发生器、分频器、指令计数器等都要使用计数器。
计数器的种类很多。
按时钟脉冲输入方式的不同,可分为同步计数器和异步计数器;按进位体制的不同,可分为二进制计数器和非二进制计数器;按计数过程中数字增减趋势的不同,可分为加计数器、减计数器和可逆计数器。
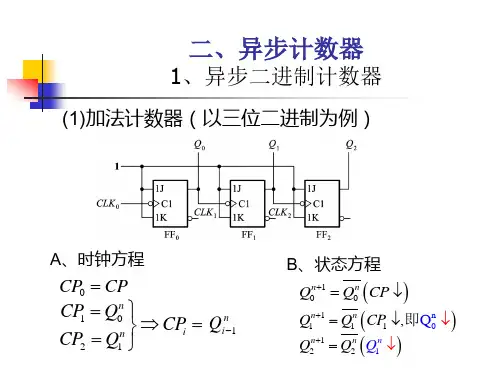
8.4.1 二进制异步计数器1.二进制异步加计数器(1)电路结构以三位二进制异步加法计数器为例,如图8.4.1所示。
该电路由3个上升沿触发的D触发器组成,具有以下特点:每个D触发器输入端接该触发器Q 端信号,因而Q n+1=Q n,即各D触发器均处于计数状态;计数脉冲加到最低位触发器的C端,个触发器的Q 端信号接到相邻高位的C端。
图8.4.1 3位二进制异步加计数器(2)原理分析假设各触发器均处于0态,根据电路结构特点以及D触发器工作特性,不难得到其状态图和时序图,它们分别如图8.4.2和图8.4.3所示。
其中虚线是考虑触发器的传输延迟时间tpd后的波形。
图8.4.2 图8.4.1所示电路的状态图图8.4.3 图8.4.1所示电路的时序图由状态图可以清楚地看到,从初始状态000(由清零脉冲所置)开始,每输入一个计数脉冲,计数器的状态按二进制递增(加1),输入第8个计数脉冲后,计数器又回到000状态。
因此它是23进制加计数器,也称模八(M=8)加计数器。
从时序图可以清楚地看到Q0,Q1,Q2的周期分别是计数脉冲(CP)周期的2倍,4倍、8倍,也就是说Q0,Q1,Q2,分别对CP波形进行了二分频,四分频,八分频,因而计数器也可作为分频器。
需要说明的是,由图8.4.3中的虚线波形可知,在考虑各触发器的传输延迟时间tpd时,对于一个n位的二进制异步计数器来说,从一个计数脉冲(设为上升沿起作用)到来,到n个触发器都翻转稳定,需要经历的最长时间是ntpd ,为保证计数器的状态能正确反应计数脉冲的个数,下一个计数脉冲(上升沿)必须在ntpd后到来,因此计数脉冲的最小周期Tmin=ntpd。




异步二进制计数器电路组成及案例说明(1)异步二进制加法计数器图8.44是用四个主从JK触发器组成的四位二进制加法计数器逻辑图。
图8.44 JK触发器组成的异步二进制四位加法计数器图中各触发器的J端和K端都悬空,相当于置1,由JK触发器的真值表知,只要有时钟信号输入,触发器的状态一定发生翻转。
图中低位触发器的Q接至高位触发器的C1端,当低位触发器由1态变为0态时,Q就输出一个下降沿信号,这个信号正好作为进位输出。
R加入负脉冲,使计数器清0。
当计数脉计数器在工作之前,一般通过各触发器的置零端d冲CP输入后,计数器就从Q3Q2Q1Q0=0000状态开始计数。
当第1个CP脉冲下降沿到达时,FF0由0态变为1态,Q0由0变1,Q1、Q2、Q3因没有触发脉冲输入,均保持0态;当第2个CP脉冲下降沿到达时,FF0由1态变为0态,即Q0由1变0,所产生的脉冲负跳变使FF1随之翻转,Q1由0变1。
但Q1端由0变为1的正跳变无法使FF2翻转,故Q2、Q3均保持0态。
依次类推,每输入1个计数脉冲,FF0翻转一次;每输入2个计数脉冲,FF1翻转一次;每输入15个计数脉冲后,计数器的状态为“1111”。
显然,计数器所累计的输入脉冲数可用下式表示:N=Q3×23+Q2×22+Q1×21+Q0×20第16个脉冲作用后,四个触发器均复位到0态。
从第17个CP脉冲开始,计数器又进入新的计数周期。
可见一个四位二进制计数器共有24=16个状态,所以四位二进制计数器可组成一位十六进制计数器。
由于各触发器的翻转时刻不同,所以这种计数器又称为异步计数器。
各触发器状态的变化及计数情况见表8.10所示。
各级触发器的状态可用如图8.45所示的波形图表示。
由图示波形可以看出,每个触发器状态波形的频率为其相邻低位触发器状态波形频率的二分之一,即对输入脉冲进行二分频。
所以,相对于计数输入脉冲而言,FF0、FF1、FF2、FF3的输出脉冲分别是二分频、四分频、八分频、十六频,由此可见N位二进制计数器具有2N分频功能,可作分频器使用。
异步二进制加法计数器教学目的:让学生掌握加法计数器的分析方法教学重点:加法计数器的分析方法教学难点:加法计数器的工作原理教学方法:讲授法教学时间:2课时教学过程:一、复习引入:复习JK触发器的逻辑功能。
二、新授:(一)、异步三位二进制加法计数器1、电路组成:由三个无空翻的T型触发器逐级串联组成的异步三位二进制加法器(也可以由无空翻的JK型触发器构成.,书上J与K同时接1就是说J=K也就是T触发器)CR2、结构特点:(1) 每个触发顺为T’型,且带直接复位端.(2) 异步工作方式.因为输入计数脉冲只送至触发器最低位F1的CP1端,因此,各触发器的改变与计数输入脉冲不同步.(3) 输出信号取自各Q 端,即Q 2 、 Q 1 、 Q 0.3、 工作原理见波形图(1)、CR 端来低电平时,计数器被清”0”,电路状态为Q 2 Q 1 Q 0=000(2)、随着输入计数脉冲个数的增加,计数器输出端Q 2 Q 1 Q 0的读数从000至111顺序递增,相当于十进制数字从0至7依次递增,所以为加法计数器.(3)、第8个计数脉冲输入后,计数器的状态回到000,这表示了一个循环,以后 每输入8 个脉冲,计数器的状态循环一次.三位二进制加法计数器的计数顺序如表6.2.1所示.4、计数与分频.(1) 从波形图可以看出,每经过一级触发器,脉冲的频率就减少一半,因此, 计数器也称为分频电路或分频器.(2) 、对于一级触发器F 1,每两个计数脉冲作用后, F 1复”0”,同时,输出一个进 位脉冲信号,所以,F 1能记录12 =2个脉冲。
从波形图看出,每2个CP 产生一 个Q 1波形,Q 1信号信号频率是CP 信号频率的1/2,即除2,故将一级(位)二进制计数器又称为2分频电路,也称除2电路.(3) 、对于二级触发器,每四个计数脉冲CP,使电路复原一次,并有并且输出一个进位脉冲信号,所以两级能记录22 =4个计数脉冲.从波形力看出,每4 个CP 产生一个Q 2波形,Q 2信号的频率是CP 频率的1/4,即除4,故将二级二进制计数器又称4分频器. 1 2 3 4 5 6 7 8Q OCP Q 1 Q 2(4)、以此类推,若计数电路由N个触发器组成,那么,可记录n2个计数脉冲,输出进位脉冲的频率是输入计数脉冲频率的1/2 ,又称为n2分频电路5、异步三位二进制加法计数器状态表:练习:把波形图擦掉后再请学生上台画,以检查学生对波形做法掌握的程度小结:计数器波形图的正确做法。