积的小数位数与乘数的小数位数的关系

四年级数学（下册）一、小数的意义和加减法小数的意义：（1）像0.7，0.45，0.025，0.107……这样，用来表示十分之几、百分之几、千分之几……的数，叫做小数。

（2）小数的计数单位为十分之一、百分之一、千分之一......分别写作0.1、0.01、0.001 ......（3）每相邻的两个计数单位之间进率是10。

（4）小数的数位是十分位、百分位、千分位...... 小数最高位是十分位，整数部分最低位是个位。

数位顺序表：（6页）单位的变换：（1）分清是低级单位变换成高级单位，还是高级单位变换成低级单位，决定是乘进率还是除以进率。

（2）分清改写的两个单位之间的进率是多少。

（3）确定小数点应向哪个方向移动，移几位。

例如：①350千克=（0.35）吨350千克÷1000（进率）=0.32吨低级单位÷进率＝高级单位小数点往右移②3.02吨=（3020 ）千克3.02吨×1000（进率）=3020千克高级单位×进率＝低级单位小数点往左移小数的基本性质：小数的末尾添上“0” 或去掉“0”，小数的大小不变。

例如：3.20=3.2 5.10=5.10.1与0.10的区别联系：（1）区别：0.1表示1个0.1 ，0.10表示10个0.01，意义不同。

（2）联系：0.1=0.10 两个数大小相等。

单位的换算：（1）钱币单位：1元=10角=100分 1角=10分1角=110元=0.1元 1分=110角=0.1角（2）长度单位：1米=10分米=100厘米 1分米=10厘米1厘米=10毫米 1厘米=1100米=0.01米 36厘米=36100米=0.36米（3）面积单位：1平方千米=100公顷1公顷=10000平方米 1平方米=100平方分米1平方分米=100平方厘米 （4）质量单位：1吨=1000千克=1000000克 1千克=1000克1克=11000千克=0.001千克 12克=121000千克=0.012千克（5）时间单位：1天=24时 1时=60分=3600秒 1分=60秒比较小数的大小：先比较整数部分，整数部分大的那个数大；整数部分相同就要看十分位，十分位上大的那个数大；十分位上相同，就要看百分位，百分位上大的那个数大 计算小数加减法就注意小数点对齐。

1、（1）每支铅笔0.4元，买3支铅笔需要多少钱？涂一涂，算一算。

（）○（）=（）（元）（2）交流展示。

师：你是怎么计算的？你觉得要用这实际是在求什么？生：实际是求3个0.4的和是多少。

师总结：小数乘整数的意义就是求几个相同加数的和的简便运算。

这个小朋友有哪些地方值得你学习？（主要学习画图规范）下面这个问题你能独立解决吗？2、（1）根据735×16=11760，在（）内填上适当的数。

（）×（）=1.176（3）交流展示。

师：你是怎么想的？生：...师：你说的真好，一定不要忘记末位的0哦，孩子们，你们觉得这个题目是想考察孩子们哪一个知识点呢？生：积的小数位数等于乘数的小数位数之和。

师：你们找的真准确，表扬你们。

3、（1）师：不计算，下面的结果正确吗？思考一下。

9.81×1.1=9.791（2）汇报交流。

师：你是怎么判断的？生：因为1.1大于1，所以1.1×9.81的积应该比9.81大，而9.791小于了9.81.师：谁能再来说一说这个判断理由。

（请两个学生，再让同桌互相说一说）（3）我们刚刚初步判断9.81×1.1=9.791是错误的，现在要用竖式计算一下。

下面的竖式计算正确吗？（出示9.81×1.1的竖式）生：末位没有对齐。

师：小数竖式计算时需要注意些什么？生：末位对齐；按照整数乘法计算的方法算出积，再看乘数中一共有几位小数，有几位，就从积的末位起向左数出几位，再点上小数点。

如果积的末位有0要先点上小数点，再去掉小数末尾的0.如果积的位数不够怎么办？像这种（出示0.12×0.06的竖式）生：在乘的整数积的前面添0补位，再点上小数点。

师：那这个竖式对不对呢？你能改在旁边吗？师：当小数和整十整百数相乘时，整十整百数0前面的数和末位对齐，然后再按整数乘法计算的方法算...5、（1）计算下面各题，能简算就简算。

活动二：。

新北师大数学小升初复习知识要点第一部分：小数1、小数的意义：把单位“1”平均分成10份、100份、1000份……取其中的1份或几份，表示十分之几、百分之几、千份之几……的数，叫小数。

2、（1）除数是整数的小数除法（如：51.75/15)只要注意商的小数点要与被除数的小数点对齐,有余数的在余数后面添"0"再继续除.（2）除数是小数的小数除法，先移动除数的小数点，使它变成整数，除数的小数点向右移动几位，被除数的小数点也向右移动几位（位数不够的，在被除数的末尾用“0”补足，然后按照除数是整数的小数除法进行计算。

3、比较小数的大小：先比较整数部分，整数部分大的那个数大；整数部分相同就要看十分位，十分位上大的那个数大；十分位上相同，就要看百分位，百分位上大的那个数大……4、计算小数加减法就注意小数点对齐。

（1）小数加、减法的意义：小数加减法的意义与整数加减法的意义相同。

①小数加法的意义：把两个数合并成一个数的运算。

②小数减法的意义：已知两个加数的和与其中的一个加数，求另一个加数的运算。

（2）小数的基本性质：小数末尾添上“0”或去掉“0”，小数的大小不变。

（3）小数加减计算法则：小数点对齐；按照整数加减法的法则计算。

从末位算起；哪一位上的数相加满十，要向前一位进一。

如果被减数的小数末尾位数不够，可以添“0”再减，哪一位上的数不够减，要从前一位退一，在本位上加十再减；得数的小数点要对齐横线上的小数点。

（4）小数加减混合运算的顺序和整数加减混合运算的顺序相同。

同级运算，从左往右；有括号的，先里后外。

（5）整数加、减法的运算定律同样适用于小数加减法。

5、小数加减混合运算要选择简便的方法进行运算。

6、小数末尾添上“０”或去掉“０”，小数大小不变。

(3.20=3.2)7、小数点移动引起小数大小变化的规律：小数点向左移动一位，这个数就缩小到原来的（1/10 ），小数点向左移动两位，这个数就缩小到原来的（1/100 ），……小数点向右移动一位，这个数就扩大到原来的（10倍），小数点向右移动两位，这个数不扩大到原来的（100倍），……8、积的小数位数与乘数的小数位数的关系：（1）两个乘数共有几位小数，积就有几位小数。

北师大版四年级数学（下册）知识点一小数的认识和加减法【知识要点】数的意义1、小数的意义：把单位“1”平均分成10份、100份、1000份……取其中的1份或几份，表示十分之几、百分之几、千份之几……的数，叫小数。

2、分母是10、100、1000……的分数可以用小数表示，表示十分之几的小数是一位小数、表示百分之几的小数是两位小数、表示千分之几的小数是三位小数……3、小数的组成：以小数点为界，小数由整数部分和小数部分组成。

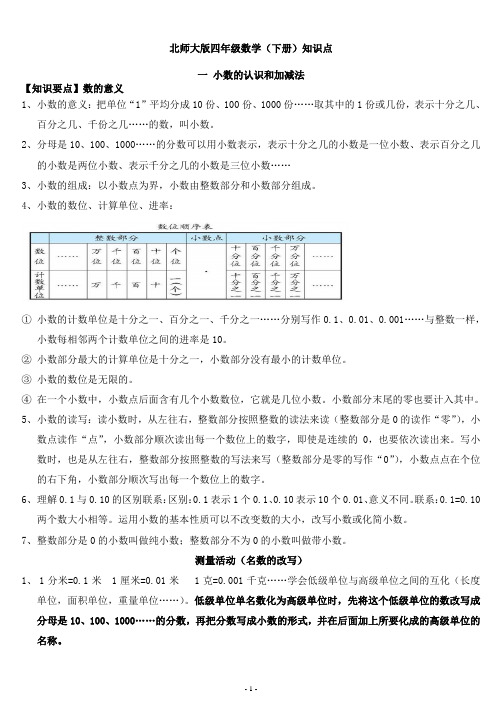
4、小数的数位、计算单位、进率：①小数的计数单位是十分之一、百分之一、千分之一……分别写作0.1、0.01、0.001……与整数一样，小数每相邻两个计数单位之间的进率是10。

②小数部分最大的计算单位是十分之一，小数部分没有最小的计数单位。

③小数的数位是无限的。

④在一个小数中，小数点后面含有几个小数数位，它就是几位小数。

小数部分末尾的零也要计入其中。

5、小数的读写：读小数时，从左往右，整数部分按照整数的读法来读（整数部分是0的读作“零”），小数点读作“点”，小数部分顺次读出每一个数位上的数字，即使是连续的0，也要依次读出来。

写小数时，也是从左往右，整数部分按照整数的写法来写（整数部分是零的写作“0”），小数点点在个位的右下角，小数部分顺次写出每一个数位上的数字。

6、理解0.1与0.10的区别联系：区别：0.1表示1个0.1、0.10表示10个0.01、意义不同。

联系：0.1=0.10两个数大小相等。

运用小数的基本性质可以不改变数的大小，改写小数或化简小数。

7、整数部分是0的小数叫做纯小数；整数部分不为0的小数叫做带小数。

测量活动（名数的改写）1、1分米=0.1米 1厘米=0.01米 1克=0.001千克……学会低级单位与高级单位之间的互化（长度单位，面积单位，重量单位……）。

低级单位单名数化为高级单位时，先将这个低级单位的数改写成分母是10、100、1000……的分数，再把分数写成小数的形式，并在后面加上所要化成的高级单位的名称。

积随乘数变化与竖式计算【知识梳理】知识点一、积随乘数变化的规律1、在乘法中，一个乘数扩大到原来的()0≠m m 倍，另一个乘数扩大到原来的()0≠n n 倍，则积扩大到原来的n m ⨯倍。

2、在乘法中，一个乘数缩小到原来的()01≠m m ，另一个乘数缩小到原来的()01≠n n，则积缩小到原来的nm 11⨯（或n m ⨯1）。

知识点二、积的小数位数与乘数的小数位数的关系在小数乘法中，两个乘数一共有几位小数，积就有几位小数。

知识点三、小数乘法的竖式计算方法小数乘法的竖式计算方法：先按照正数乘法算出积，再看乘数中一共有几位小数，就从积的末位起向左数出几位，点上小数点。

积的位数不够时，先在乘得的整数积的左边添“0”补位，再点上小数点。

积的小数末尾有0的，要去掉小数末尾的0。

【经典例题】例1、想一想，填一填。

4 扩大到原来的（ ）倍 4 0 缩小到原来的10010. 4 × 2 扩大到原来的10倍 ×（ ） 缩小到原来的（ ） ×（ ） 8 扩大到原来的（ ）倍 （ ） 缩小到原来的（ ） （ ）举一反三：1、根据第一栏的积很快写出后面每栏的积。

例2、根据24×16=384，在（ ）里填上合适的数。

（ ）×（ ）=38.4 （ ）×（ ）=3.84 （ ）×（ ）=0.384 （ ）×（ ）=384举一反三：2、根据97×25=2425，把下面的算式填完整。

（ ）×（ ）=24.25 （ ）×（ ）=0.2425 （ ）×（ ）=25250 （ ）×（ ）=2.425例3、用竖式计算。

6.2×0.15= 0.27×0.9= 8.5×0.6=举一反三：3、用竖式计算。

6.2×1.6= 0.27×1.8= 8.5×0.07=例4、两个乘数的积是75.2，其中一个乘数扩大到原来的6倍，另一个乘数缩小到原来的21，积是多少？举一反三：4、在一个乘法算式中，两个乘数一个扩大到原数的1000倍，一个缩小到原来的101，得到的新的结果是156.32，那么原来的结果是多少？【巩固练习】一、填空。

2021—2022学年度第二学期北师大版四年级数学三 小 数 乘 法 单元复习一、口算小数乘法1.小数乘整数的意义:求几个相同加数的和的简便运算。

小数乘法的意义比整数乘法的意义有了进一步的扩展。

小数乘法的意义包括两种情况:一是同整数乘法的意义相同,即求几个相同加数的和的简便运算;二是求一个数的十分之几,百分之几……是多少。

如1.5×3表示1.5的3倍是多少或3个1.5相加的和是多少。

2.小数乘整数口算方法:先按整数乘法的法则算出积,再看乘数中一共有几位小数,就从积的右边起数出几位点上小数点。

如0.2×4=0.8。

口算0.2×4时,先算2×4=8,乘数中有一位小数,所以0.2×4的积也是一位小数,即0.2×4=0.8。

二、小数点的变化规律1.小数点移动引起小数大小变化的规律:①把一个小数扩大到原来的10倍、100倍、1000倍……只要把小数点向右移动一位、两位、三位……位数不够时,要用“0”补足。

②把一个小数缩小到原来的110,1100,11000,…只要把小数点向左移动一位、两位、三位……位数不够时,要用“0”补足。

如1.2×10=12;1.2÷100=0.012。

计算1.2×10时,就是把1.2扩大到原来的10倍,小数点向右移动一位,即1.2×10=12;1.2÷100,就是把1.2缩小到原来的1100,小数点向左移动两位,即1.2÷100=0.012。

2.数小数点的方法:①数数字,②数间隔。

三、不进位的小数乘法1.积的小数位数与乘数的小数位数的关系:小数乘法中各个乘数中小数的位数和就是这道题中积的小数位数。

如1.2×0.8=0.96。

计算1.2×0.8时,先算出12×8=96,乘数中一共有两位小数,积是两位小数,即1.2×0.8=0.96。

北师大版四年级上册数学练习五教案例文北师大版四年级上册数学练习五教案例文1教学目标:1、结合具体情境,探索积的小数位数与乘数的小数位数的关系。

2、让学生在比较中学会观察,学会总结。

3、渗透科学的思维方法。

教学重点:探索积的小数位数与乘数的小数位数的关系。

教学难点:探索积的小数位数与乘数的小数位数的关系。

教学设计一、创设问题情境:1、出示一张测量表:这是小强学习测量以后,课外测量的几组数据。

你能根据这些数据算出它们的面积吗街心广场长30米宽20米花坛长3米宽2米地板砖长0.3米宽0.2米(1)学生独立列式计算后,汇报。

(2)教师根据学生的汇报,板书出3个算式:街心广场: 30×20=600(平方米)花坛: 3×2=6(平方米)地板砖: 0.3×0.2=二、探索积的小数位数与乘数的位数之间的关系。

1、讨论:街心广场和花坛面积之间有什么关系它们的长与宽之间又有什么关系总结:长与宽都扩大到原来10倍,面积扩大——100倍;长与宽都缩小到原来10倍,它的面积就缩小到原来的100倍。

缩小到原来的100倍也可以说是缩小到原数的1/100,小数点向左移动2位。

2、小组讨论:我们应用刚才发现的现象,来比较花坛和地板砖的面积之间有什么关系地板砖与屏幕相比,长和宽都缩小到原来的10倍,它的面积也就缩小到原来的100倍。

所以它的积也会缩小到原来的100倍。

结果是0.06平方米。

3、这种方法得出来的结果是否正确你能用其它的方法验证吗(可以引导学生从直观涂一涂的方法来验证刚材的结论是否正确。

)4、引导学生总结:在小数乘法中,我们可以先把它们看成是整数来算,然后再看乘数的末尾一共有几位小数,就在积的末尾数出几位小数点上小数点。

三、尝试练习,再探规律。

1、试一试:根据第一算式求下面2个算式的积。

让学生说说怎样算的。

2、填一填:将上一题的计算结果填入表格中。

然后观察积的小数位数与乘数的小数位数之间有什么关系。

北师大版四年级数学下册第三单元《小数乘法》【知识框架】小数乘法的意义1、小数点移动引起小数大小变化的规律2、积的小数位数与乘数的小数位数的关系3、计算小数乘法会用竖式计算小数乘法及估算4、小数的混合运算（整数运算定律完全适合小数）【知识要点】文具店（小数乘法的意义）通过具体情境教学使学生了解小数与整数相乘就是表示几个相同加数的和的简便运算。

第一课时1、小数乘法的意义小数乘法的意义比整数乘法的意义，有了进一步的扩展．小数乘法的意义包括两种情况：一是同整数乘法的意义相同，即求相同加数的和的简便运算．二是求一个数的十分之几,百分之几……是多少练习：直接写出得数。

0.6×0.8 3×0.9 2.5×0.4 3.6×0.480×0.3 1.1×912.5×8 50×0.042、小数的计算法则计算小数乘法，先按照整数乘示的法则算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点．小数计算乘法，用的是转化的思想方法．先把小数转化为整数算出积，再确定小数点的位置，还原成小数乘法的积．如6．2×0．3看作62×3相乘的积是186，因数中一共有两位小数，就从186的右边起数出两位，点上小数点还原成小数乘法的积1．86．因此，小数乘法的关键是处理好小数点．在点小数点时注意，乘得的积的小数位数不够时，要在前面用0补足，如0．04×0．2=0．008，在8的前面补两个0，点上小数点后，整数部分也写一个0．练习1、4.09×0.05的积有（）小数，5.2×4.76的积有（）位小数。

2、根据13×28=364，很快地写出下面各式的积。

1.3×2.8= 0.13×0.28= 13×2.8=0.013×28= 0.13×2.8= 1.3×0.028=3、在（）里填上>、<或=163×0.8（）163 36×2.8（）364、判断题（正确的打√，错误的打×）①、0.03与0.04的积是0.12。